空间薄膜结构充气展开研究

院老虎，康 雪，连冬杉，陈源强，翟柯嘉

（沈阳航空航天大学航空宇航学院，沈阳110121）

许多大型空间结构的展开机构都是由空间薄膜制成，是一种发展前景较好的空间结构，与传统的机械展开方式相比，能够在一定程度上节约任务成本和降低任务风险。目前，其主要被应用在太阳帆的在轨展开、空间碎片的离轨、隧道的密封以及能量吸收系统等方面[1]。研究空间薄膜结构的展开过程平稳性，对其是否能完成空间任务具有决定性作用。

空间薄膜结构展开的理论方法有很多种，目前应用较为广泛的方法为控制体积法。Glaser 等运用了3 种充气方法对准静态薄膜进行充气展开研究，分别是控制体积法（Control volume, CV）、控制压强法（Control pressure, CP）和流⁃固耦合法（Arbitrary Lagrange⁃Euler, ALE），并进行了分析与实验[2]。程涵等基于ALE 法模拟了降落伞在低速气流下的充气展开过程，通过对数值模拟结果的分析解释了伞衣抖动以及风洞试验中伞底拍动产生巨大噪声的原因，并预测了开伞过程中的危险截面[3]。Wei 等将自支撑充气臂应用于可展开式薄膜帆上，并对该帆的折叠和展开提出了设计方案，给出了一种考虑充气压力影响的充气臂动力学特性的计算方法[4]。此外，还完成了充气重力梯度吊杆的展开动力学分析和在轨实验[5]。Block 等提出了两种超轻型可动臂的展开方式，一种是由螺旋形起重臂内部的可充气囊袋驱动，另一种是由具有直接驱动起重臂末端的电动展开装置驱动[6]。马瑞强等在Timoshenko 梁理论和哈密顿原理的基础上，推导了自支撑臂振动微分方程，进而设计出一种新型梁单元模型，其能够同时考虑充气压力的预应力和构型变化[7]。

充气薄膜具有施工周期短的优势，且有较强的抵抗地震的能力，故可应用在密封隧道上。Sosa等提出应用有限元模型进行充气展开仿真，以模拟用来密封隧道的大型充气结构的初步展开，并且对其进行了初次展开的试验研究[8⁃9]。Pecora 等模拟了用于密封隧道横截面的大规模可充气结构的放气、折叠、展开和充气的过程[10]。

随着工艺技术的发展，用来模拟薄膜的材料和结构形状都在发生着变化。Li 等以4 个小型单织物拱架和一个全尺寸织物拱架为研究对象，运用控制体积法来模拟拱架的自展开失效并揭示了膜应力的发展[11]。Sinn 等基于自充气自适应膜概念设计了一种自适应结构，通过将由局部元素引起的局部变化相加，可以对全局结构的形状变化产生显著影响[12]。韩堃烽研究了薄膜充气展开过程数值仿真中涉及的重启动、部件接触、沙漏问题及控制体积法等基本理论，并应用LS⁃DYNA 软件对大尺寸薄膜进行了折叠收纳，进而对模型进行了修正，最后对其展开合理性进行了验证[13]。肖潇对现有的充气薄膜分析模型进行了多方面的比较分析，提出了相应的修正建议，而后采用控制体积模型研究了充气薄膜结构的速度控制方法，并在此基础上对减小充气管展开端的速度提出了改进的方法[14]。Han 等设计了一种新的空间充气展开系统[15]。该系统主要包括安全、稳定、燃烧温度低、产气缓慢、环保清洁的气体发生剂，以及结构简单、重量轻、体积小、腔室灵活的气体发生剂。Zhao 等设计了一种用于充气膜结构的压力控制和载荷模拟的自动系统，包括压力控制子系统和载荷模拟子系统[16]。Ortega 等建立了一个模型，能够以足够的精度和较低的计算成本预测结构上的风荷载，从而有可能将气动弹性分析用于充气结构的常规计算[17]。Young 等使用基于三维挠性的纤维束有限元模型对带有轴向加强绳的充气环形结构构件进行结构测试，并将面内和面外实验结果与所预测的模型进行了比较。经模拟发现，为了近似实验中观察到的载荷⁃变形响应，必须仔细控制试验和模型边界条件以及载荷方案[18]。

充气薄膜结构还可以应用在航天任务中，能够在废弃卫星的寿命末期为其增加气动阻力，使其尽快坠入大气层。彭福军等在研究了空间增阻薄膜结构主要技术的基础上，进一步分析了其结构构型设计技术、长寿命材料技术、折叠展开技术和低成本设计技术等，为后续的实际应用提供了理论基础[19]。甄铎为了研究影响增阻薄膜结构失稳载荷和刚度的因素，分别从理论模型和数值计算分析了结构的几何参数、充气内压等对其完成空间任务的影响程度，并利用有限元方法对推导的结果进行了验证[20]。由于近地轨道迫切的离轨需求，张义提出了一种可自我维持阻力面积的充气增阻球离轨装置设计方案，依据近地轨道的大气摄动环境，运用有限元方法建立了计算模型，得到了影响离轨时间的主要因素[21]。Fernandez 等设计了一种利用自然日光性原理的智能太空结构，可以通过使结构改变形状并因此在单个结构中适应不同的任务要求来提高航天器的灵活性[22]。该结构的另一个优点是，在展开后可抵御微小的陨石或空间碎片撞击，具有很高的可靠性。

本文首先阐述了薄膜结构充气展开动力学的仿真理论基础，即控制体积法。而后进行了气袋模型、气袋材料、接触关键字的选择，然后对空间薄膜结构进行充气展开过程仿真，以期能为太空任务应用提供一定基础。

1 充气展开动力学理论基础

目前，应用在空间结构的充气展开仿真的方法主要是控制体积法，因为这种方法建模简单、方法成熟，所以应用较为广泛。还有另外一种方法，即流⁃固耦合法。由于现在国内外对于这种方法的研究都较少，并且应用此方法进行建模较为复杂，所以尚未被广泛应用。

控制体积法可以将载荷曲线作为气体的充入条件来模拟与薄膜结构之间的相互作用。此方法在一定程度上忽略了在充气过程中需要考虑的气体惯性问题，但又会考虑到气体产生的压强。它的基本原理是将薄膜结构的内部控制体积用假定的隔膜离散为多个连接着的空腔。这种方法假定每个时刻空腔内压强是相等的，从一个空腔流入下一个空腔的气体量是隔膜面积的函数。当充气开始进行时，隔膜截面的面积也不断增大；当薄膜结构结束展开时，隔膜截面的面积不再增大，且应与其截面积相等。理论模型和物理过程如图1 所示，其体积公式为

式中Ω 表示充气管所形成的空间封闭区域。根据格林公式，可得由其封闭曲面面积分围成的体积积分为

图1 充气薄膜结构模型Fig.1 Inflatable membrane structure model

高级有限元前后处理软件（LS⁃PREPOST）通过中心差分法对时间进行积分运算，则薄膜结构各节点在第n 个时间步结束时的加速度表达式表示如下

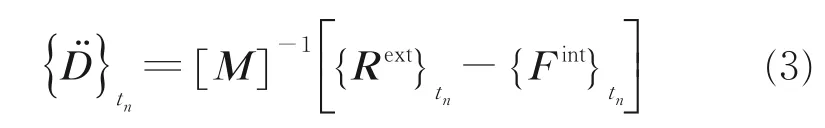
式中：∫WBTsdW 表示tn时刻单元应力场的等效节点应力；Fhg为沙漏阻力；Fcontact为接触力。

本文运用中心差分法对时间进行积分运算，通过对速度和位移的一阶中心差分计算得到结构的加速度和速度，计算分析过程如下

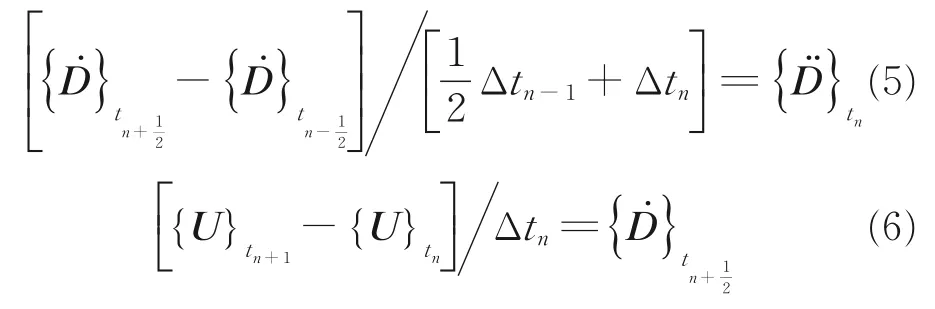
式中

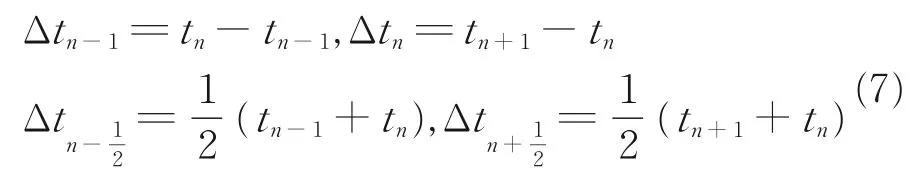
在t+Δt 时刻的位移为

式中：{D}t+Δt为结构在t+Δt 时刻的位移；{D}t为结构在t 时刻的位移；{U}t+Δt为位移增量。

式（8）中的差分形式可以表示如下

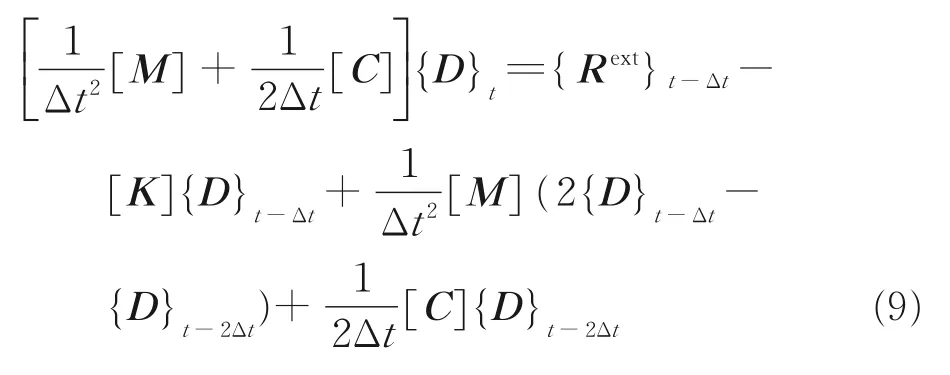
2 薄膜结构模型与展开动力学分析

2.1 概述

首先基于LS⁃PREPOST 建立了一个气球形薄膜结构的有限元模型，并针对该结构设计了不同的展开工况对其进行仿真计算，分析了改变充入气体条件时对薄膜结构展开稳定性的影响。模型建立以后，为其编辑关键字。对于薄膜结构用于仿真的气 袋 模 型 ，选 择 *AIRBAG_SIMPLE_AIR⁃BAG_MODEL，这种模型充气平稳。气袋材料使用关键字*MAT⁃FABRIC，是一种织物材料。充气薄膜结构展开的主要动力来源就是从折叠状态展开时的结构自接触，因此选择接触关键字*CON⁃TANCT_AIRBAG_SINGLE_SURFACE，并且这种方法在检查穿透时，会进行双向的检索，可以有效地防止穿透现象的产生。在薄膜结构的展开过程中会伴随着大变形和沙漏模式，为了使模型计算收敛，采取了全积分算法，即在*SECTION_SHELL 关键字中将ELFORM 项设置为9。薄膜结构的材料和几何尺寸见表1，仿真时间取为0.1 s。

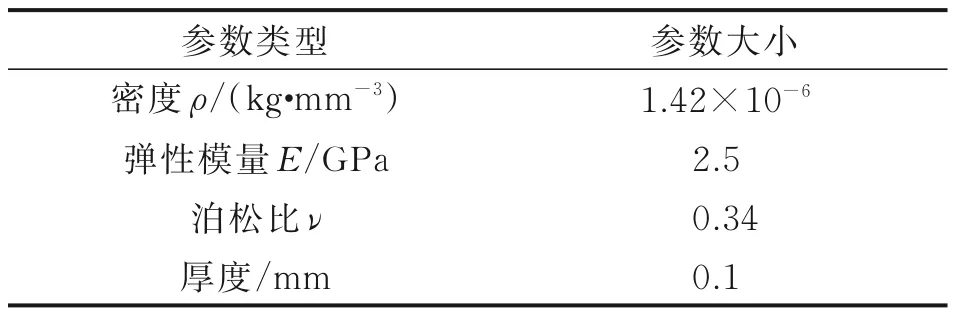
表1 薄膜结构参数Table 1 Membrane structure parameter

2.2 薄膜结构充气模型

首先选取一个标准的充气速率作为参照，在此基础之上通过修改充气载荷曲线、充入气体的温度和充入气体的压强历程曲线来对薄膜结构进行充气展开仿真。如表2 所示，可以得到在不同工况下，薄膜结构的充气展开的情况，并进行比对与分析。

表2 工况名称及标号Table 2 Working condition name and label

在第1 种工况下，充气载荷曲线如图2 所示。

图2 充气载荷曲线（工况1）Fig.2 Inflatable load curve（Working condition 1）

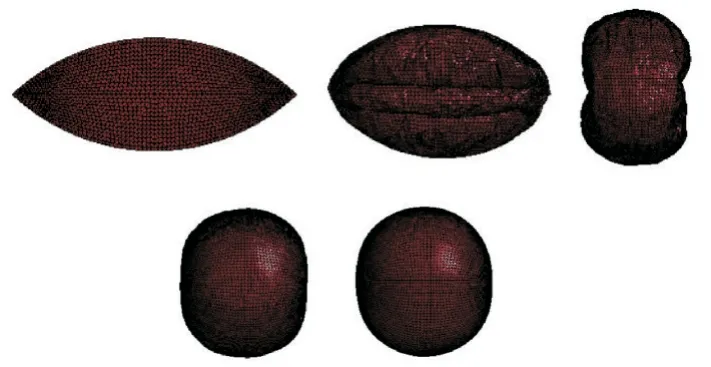
图3 充气模型及其展开历程（工况1）Fig.3 Inflatable model and its deployed process (Working condition 1)

图4 薄膜结构体积曲线（工况1）Fig.4 Membrane structure volume curve (Working condition 1)

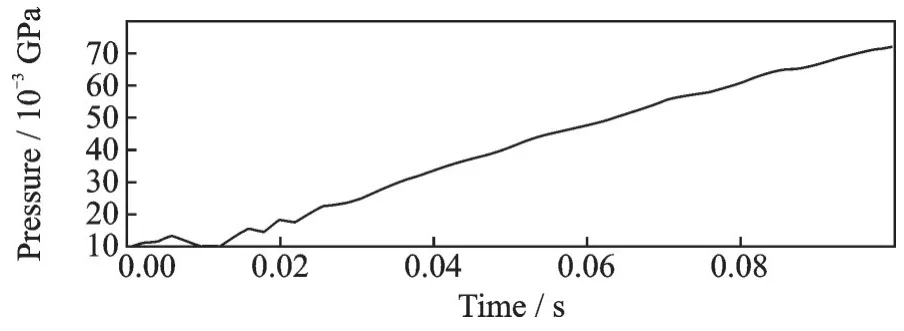
图5 薄膜结构压强曲线（工况1）Fig.5 Membrane structure pressure curve (Working condition 1)

图6 薄膜结构表面积曲线（工况1）Fig.6 Membrane structure surface area curve (Working condition 1)

图7 薄膜结构von-mises 应力（工况1）Fig.7 Von⁃mises stress of membrane structure (Working condition 1)

从图2 中的充气载荷曲线可以知道，气体载荷以较快的速率充入薄膜结构内，这是因为在初始充气阶段需要一定的充气压力使折叠结构展开，随着展开过程的进行，充气速率逐渐变缓。在图2 所示的充气载荷作用下，薄膜结构的充气展开过程如图3 所示，在展开过程中的各特性曲线如图4～6所示。

由图4 可见，在初始充气阶段，气体的内能较快地转化为结构展开的动能，薄膜结构展开得较快，体积增大得较为迅速。这是因为在初始阶段，需要利用充气速率使折叠状态的薄膜结构展开。在0.04 s 左右，体积逐渐趋于一个平稳展开的趋势。由图5 可见，在充气过程刚开始进行时，压强有波动现象，若没有采取全积分单元算法,则有可能会发生计算发散。从图6 可看出，薄膜结构的表面积从0.33 m2逐步增加到0.395 m2，在展开过程中表面积存在回弹的现象，与图4 相对应，在0.04 s之后开始平稳展开，在0.04 s 以后，压强也开始平稳增长。图7 所示为薄膜结构展开过程的von⁃mis⁃es 应力云图，可以看出，随着展开过程的进行，薄膜结构内的应力不断增大，完全展开后应力最小值为8.089 kPa，最大值为63.55 kPa，应力分布梯度不大。综合图3 可以看出，薄膜结构的展开效果较好。

在第2 种工况下，对薄膜结构的充气速率进行改变，将工况1 下的充气载荷曲线改为图8 所示的曲线。

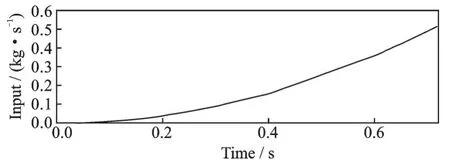
图8 充气载荷曲线（工况2）Fig.8 Inflatable load curve (Working condition 2)

图9 充气模型及其展开历程（工况2）Fig.9 Inflatable model and its deployed process (Working condition 2)

由图9 和图10 可见，充气展开过程明显较前一种工况平稳，这是由于充气速率变得缓慢所导致的。薄膜结构内的压强波动较小，但展开后的薄膜结构存在面内凹陷的情况，与工况1 相比，这显然不是理想的结果。由图11 和图12 可见，刚开始充入气体时，薄膜结构由于受到挤压，体积和表面积增加得并不明显，当充气压力持续增加时，薄膜结构开始克服自身的弹性势能进行充气展开。在0.06 s 时，薄膜结构的体积只有0.1 m3左右，而表面积却达到了1.05 m2左右，因此需要更大的内部压力才能使结构完全展开。图13 所示为薄膜结构展开过程的von⁃mises 应力云图，可以看出，薄膜结构完全展开后应力最小值为52.6 kPa，最大值为314.1 kPa。与工况1 相比，结构内的应力较大，展开效果不理想，且这种模型计算速度缓慢，需要一定的计算时间。

在第3 种工况下，将工况1 的模型充入气体温度改为750 K，充入气体的载荷曲线保持不变，则薄膜结构的充气展开过程如图14 所示。

图10 薄膜结构压强曲线（工况2）Fig.10 Membrane structure pressure curve (Working condition 2)

图11 薄膜结构体积曲线（工况2）Fig.11 Membrane structure volume curve (Working condition 2)

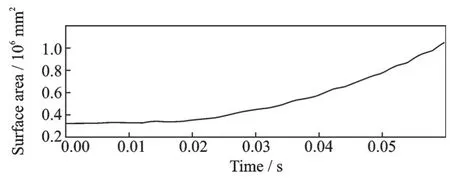
图12 薄膜结构表面积曲线（工况2）Fig.12 Membrane structure surface area curve (Working condition 2)

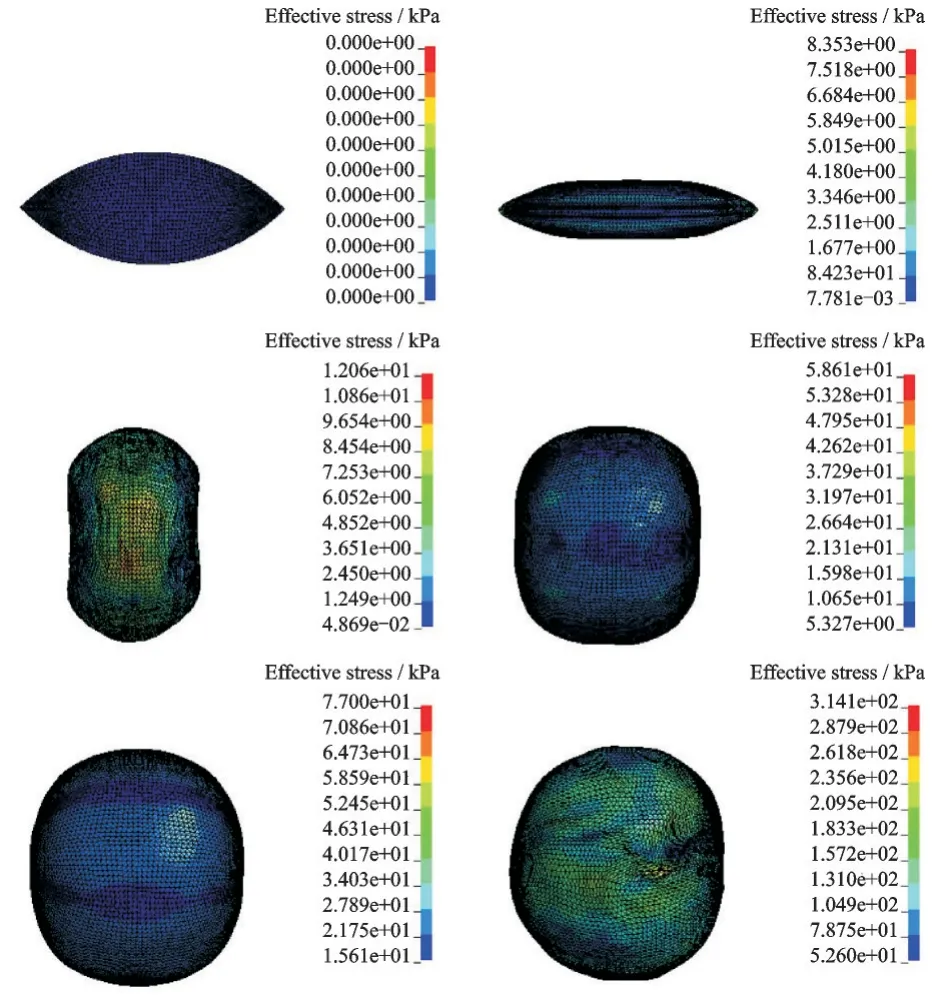
图13 薄膜结构von-mises 应力（工况2）Fig.13 Von⁃mises stress of membrane structure (Working condition 2)

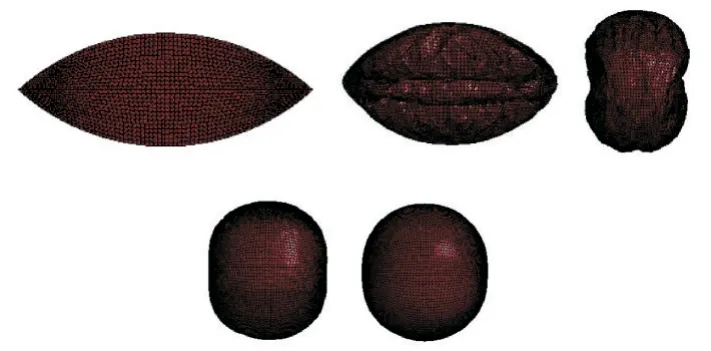
图14 充气模型及其展开历程（工况3）Fig.14 Inflatable model and its deployed process (Working condition 3)

通过图14 可以看出，与工况2 相比，充气速度明显变快，但比工况1 的充气过程平稳些。由图15可以看出，薄膜结构展开的速度较快，能够完全展开。同时可从图16 和17 看出，在此工况下仍然存在压强波动的现象，但总体的展开效果良好，薄膜结构展开后的体积和表面积均达到了预期的效果，展开过程平稳。图18 所示为薄膜结构展开过程的von⁃mises 应力云图，可以看出，薄膜结构完全展开后应力最小值为7.618 kPa，最大值为57.84 kPa，比工况1 下的应力小，并且在此工况下薄膜结构不仅能够完全展开，还可以保证展开过程的平稳性，是一种理想的展开工况。

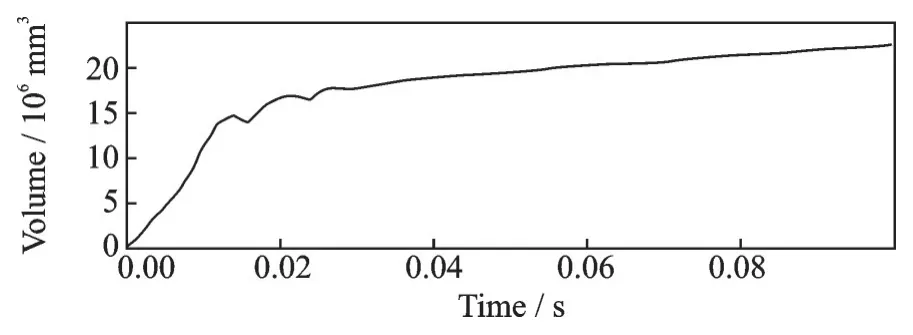
图15 薄膜结构体积曲线（工况3）Fig.15 Membrane structure volume curve (Working condition 3)

图16 薄膜结构压强曲线（工况3）Fig.16 Membrane structure pressure curve(Working condition 3)

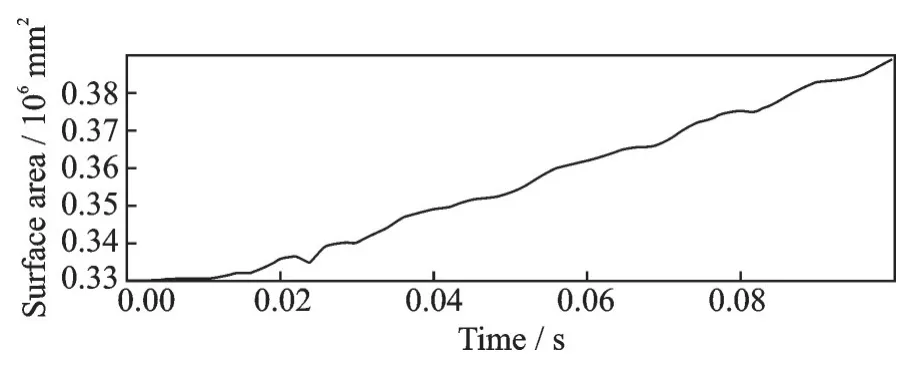
图17 薄膜结构表面积曲线（工况3）Fig.17 Membrane structure surface area curve (Working condition 3)

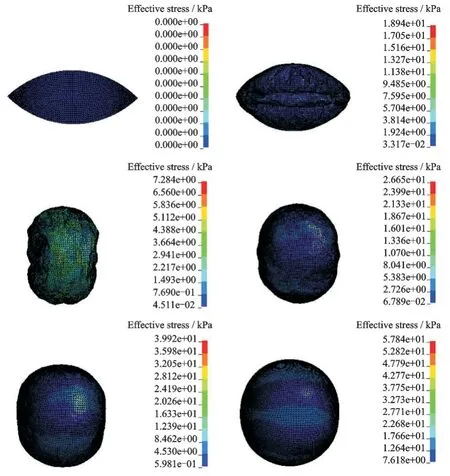
图18 薄膜结构von-mises 应力（工况3）Fig.18 Von⁃mises stress of membrane structure (Working condition 3)

在第4 种工况下，通过改变充入气体的载荷曲线来改变充入气体的压强，将工况1 下的模型充气载荷曲线改为图19 所示的曲线。

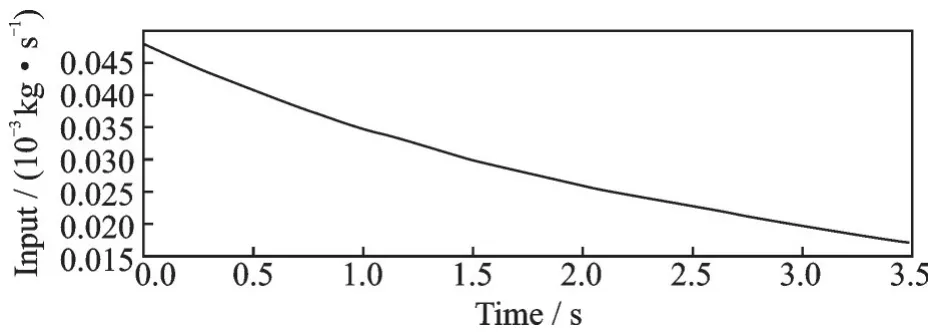
图19 充气载荷曲线（工况4）Fig.19 Inflatable load curve (Working condition 4)

从图19可以看出，比工况1下的充气速率慢，但是比工况2 下的充气速率快。在图19所示的充气载荷作用下，薄膜结构的充气展开过程如图20所示。

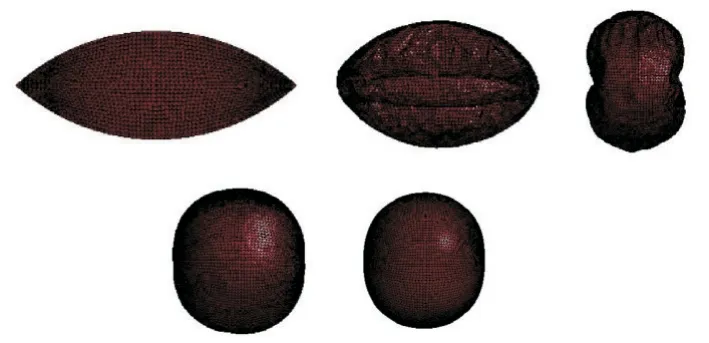
图20 充气模型及其展开历程（工况4）Fig.20 Inflatable model and its deployed process (Working condition 4)

由图20、21 和22 可以看出，薄膜结构可以完全展开。但是由薄膜结构的体积曲线可见，体积的波动现象存在于整个充气展开过程中，这不是理想的展开效果。从图23 可以看出，在0.01 s 左右，薄膜结构内的压力发生了回弹的现象，这不利于薄膜结构的顺利展开，且展开过程中的薄膜结构存在畸形现象，可以通过在接触关键字中将摩擦因数设置小些来防止结构产生畸形。从图24 可以看出，薄膜结构完全展开后应力最小值为7.298 kPa，最大值为56.6 kPa，比工况3 下的应力小，但是展开过程的平稳性不如工况3。

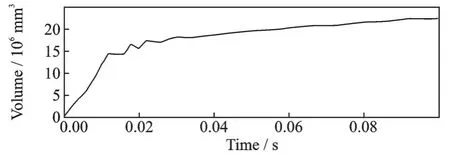
图21 薄膜结构体积曲线（工况4）Fig.21 Membrane structure volume curve (Working condition 4)

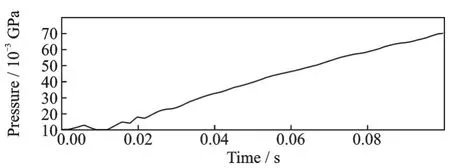
图22 薄膜结构表面积曲线（工况4）Fig.22 Membrane structure surface area curve (Working condition 4)

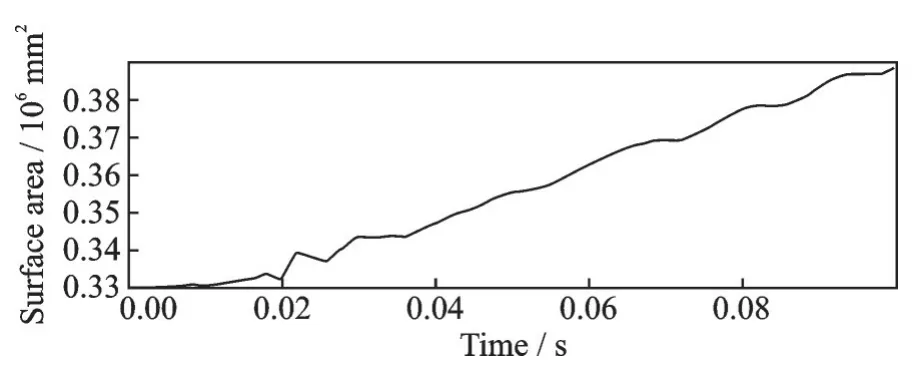
图23 薄膜结构压强曲线（工况4）Fig.23 Membrane structure pressure curve (Working condition 4)

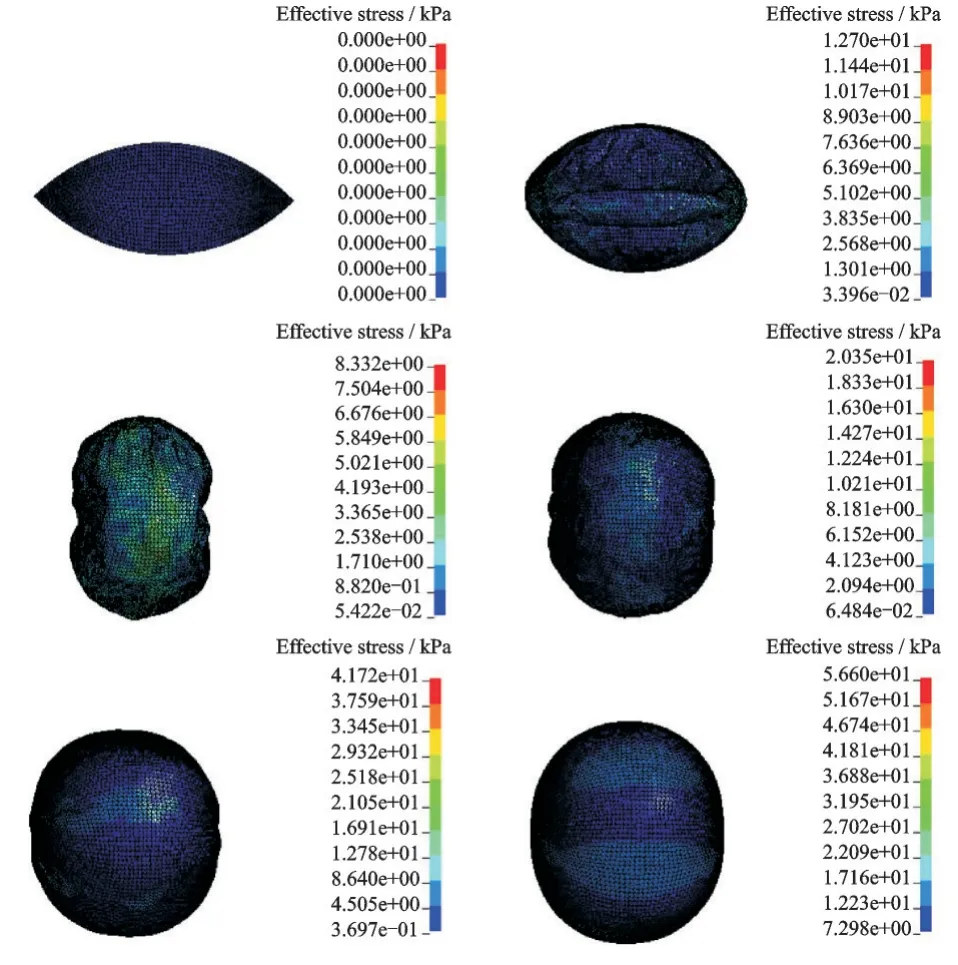
图24 薄膜结构von-mises 应力（工况4）Fig.24 Von⁃mises stress of membrane structure (Working condition 4)

3 结 论

本文以气球形薄膜结构为研究对象，在确定结构设计整体方案的基础上，在LS⁃PREPOST 中完成了有限元模型的建立和关键字的定义，将设定的4 种充气条件输出的K 文件导入LS⁃DYNA 求解器中进行了仿真分析。结果表明：通过对薄膜结构的充气模型及其展开历程、薄膜结构体积和压强等曲线的对比和分析可以得出，当调整充气温度为750 K 时，展开速度较快，且能够完全展开，展开效果良好。当降低充气速率时，展开过程会较慢，会耗费一定的时间，且在展开过程中会存在一定的扭曲现象，进而导致薄膜结构不能够完全展开，不利于实际工程应用。当改变充入气体的压强时，薄膜结构内的压力发生了回弹的现象，体积的波动现象存在于整个充气展开过程中，进而导致展开过程中的薄膜结构存在畸形现象，不利于薄膜结构的顺利展开。