基于数据驱动高阶学习律的轮式移动机器人轨迹跟踪控制

李佳伟 林娜 池荣虎

0 引言

随着机器人技术的快速发展和社会的不断进步,轮式移动机器人(Wheeled Mobile Robot,WMR)凭借简单的机械结构、稳定的运行状态和强大的环境适应能力等独特的优势不仅被广泛应用于汽车生产和农产品种植等领域,在国家安全和空间探索等方面也发挥着重要作用[1-3].由于轮式移动机器人在各领域的广泛应用,其运动控制的关键问题包括路径规划、路径跟踪和运动避障等引起了研究人员的广泛关注.其中,路径跟踪[4-6]已成为当前研究的热点之一.

WMR本质上是一个强耦合、欠驱动、多变量非线性系统[6-8],其轨迹跟踪控制器设计存在许多困难和问题,许多专家学者对此做了大量的研究工作.考虑到轮式移动机器人操作过程中未知的参数变化和外部干扰,文献[9]提出了一种基于改进非线性状态观测器的开关增益自适应滑模控制器;文献[10]提出了一种基于神经网络优化的鲁棒模型预测控制方法,提高了模型预测控制的计算效率.

值得注意的是,目前大部分的研究工作都是基于模型的控制方法以实现路径跟踪,控制性能取决于模型精度,因此很难满足实际工作要求.同时,数据驱动控制[11-14](Data-Driven Control,DDC)在处理复杂动态过程的控制问题方面变得越来越流行,技术的进步使得获取和存储操作数据变得更加容易.DDC设计的原理是利用从实际系统中获得的测量数据来设计控制器,而不使用任何显式的辨识模型信息.

在实际工况中,WMR经常需要执行重复的任务[15],如播种和喷洒作业的农用车辆和无人清扫车清扫公园环境路面、智能机器人执行搜索和巡逻任务等.在有限的时间内,它的工作环境和期望轨迹是重复不变的.对于重复运行的系统,迭代学习控制[16-19](Iterative Learning Control,ILC)提供了一种新的控制器设计思想，它可以在固定的时间间隔内,通过利用之前迭代的误差信息来更新当前输入,实现控制性能改善.

目前,WMR的ILC设计也已经有一些报道．文献[20]通过引入自适应遗忘因子,提出了一种开环PD型ILC控制器,增强了ILC的鲁棒性和稳定性;文献[21]设计了一种新的迭代学习算法,突破了传统ILC中对参考轨迹和初始位置每次迭代必须相同的限制.然而,目前大多数ILC控制方法的学习增益往往是固定不变的,而且控制过程中只使用前一次迭代的控制信息.

基于以上分析,本文针对重复运行的WMR系统提出了一种高阶迭代学习控制方法.首先,建立WMR联合直流电机的运动学方程,引入迭代动态线性化方法(Iterative Dynamic Linearization,IDL)[22-23],将WMR系统表示为线性输入输出数据模型;其次,通过设计含有附加输入信息的目标函数,建立了高阶学习控制律,利用参数更新律对控制律中的未知参数估计;最后,仿真结果验证了所提方法的有效性.

本文的创新点在于:

1)与现有的ILC方法相比,控制器设计和分析过程只使用系统输入/输出(I/O) 数据,不包含任何显式的模型信息;

2)通过采用高阶算法,在控制律中利用更多之前迭代的输入信息,提高了控制性能;

3)相比于传统的ILC 方法,学习增益是自适应变化的而不是固定不变的,提高了控制算法的鲁棒性.

本文余下结构分布如下:第1节是基本问题描述,将WMR模型利用IDL转化为线性输入输出数据模型;第2节是控制器的设计;第3节利用仿真结果验证了所提方法的有效性;第4节总结全文.

1 问题描述

WMR多采用双后轮驱动和双前轮支撑方式,前轮为用于平衡的无动力方向轮,驱动轮采用独立直流伺服电机(DC)驱动.在不考虑轮胎和地面横向滑动的情况下,WMR可以简化为两轮车模型进行运动学分析,如图1所示.

图1 轮式机器人简图Fig.1 Schematic diagram of WMR

假设图1中MWR的两个驱动轮有相同的物理特性,r为驱动轮的半径,2R为两轮之间的距离.两个轮子的中点为C点.设MWR的质心为C点,其位置坐标可设为(x,y).I是C点的惯性力矩,m是MWR的质量.

以点C为坐标原点,以MWR的前进向方向为X轴,前进方向的垂直方向为Y轴,建立机体坐标系CXcYc.机体坐标系与惯性坐标系之间的夹角为θ,即MWR的转向角.

记q(t)=[x(t)y(t)θ(t)]T表示WMR的广义坐标,x(t)和y(t)分别表示MWR在平面坐标系中的横坐标和纵坐标,θ(t)是WMR的转向角,点C表示WMR当前位置,当前线速度为v(t),角速度为ω(t),则纯滚动、无滑移情况下,MWR的非完整约束方程为

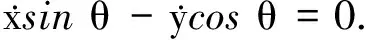
(1)

根据式(1)可得:

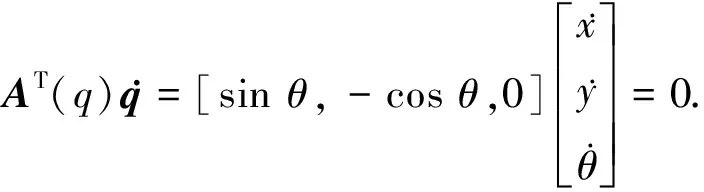
(2)

则WMR的运动学方程可以表示为

(3)

式(3)可被简化为

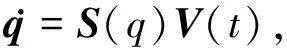
(4)

其中,

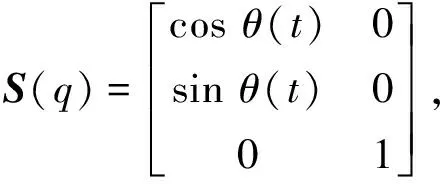
V(t)=[v(t),w(t)]T,

假设WMR在水平面上运动,不考虑表面摩擦,可以利用经典拉格朗日动力学方程得到WMR的动力学模型,如式(5)所示

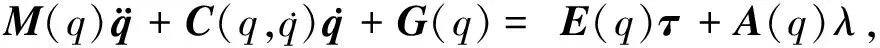
(5)

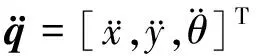
由于WMR的轨迹局限于水平面,系统势能保持不变,系统动能可以表示为

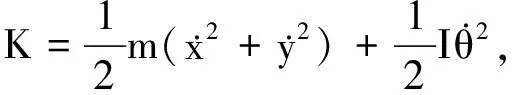
(6)

其中,m为WMR的质量,I为惯性矢量.

则

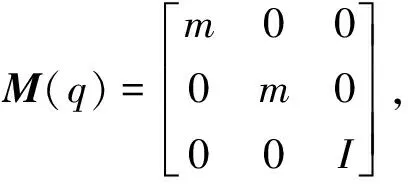
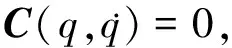
式(5)可重写为

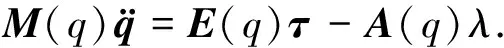
(7)

对式(4)两边求导数可得:

(8)

将式(8)代入式(7)可得:

STMSV+STMSV=STEτ-STAλ,

(9)

其中,

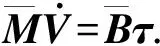
(10)

为了在式(5)中增加执行机构动力,假设WMR的驱动轮由两个有机械齿的电刷直流电机(DC)驱动,电机的数学模型为

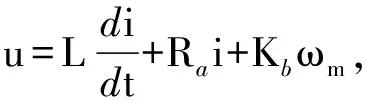
(11)

其中,u代表输入电压,Ra表示电枢电阻,L表示电枢电感,ωm表示为DC的角速度,Kb表示反电动势(Back Electromotive Force,EMF)常数.

假设在忽略电枢电感的情况下,由直流转矩与电流的关系和齿轮前后角速度与转矩的关系可得两驱动轮的扭矩为

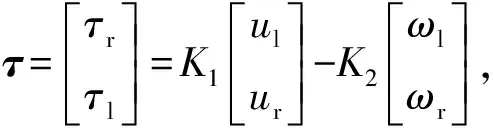
(12)

其中：K1=nKτ/Ra，K2=nKbK1,n为齿轮传动比,Kτ为直流的转矩常数；u=[ulur]T为输入电压，ul和ur分别为驱动左右轮输入电压;ωl和ωr分别为左右驱动轮的角速度;ωl和ωr分别为左右驱动轮的角速度.

根据速度矢量V与车轮角速度ωw(ωw=ωm/n)的关系可知:

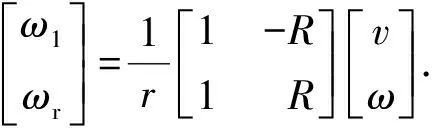
(13)

将式(12)代入式(13)可得:

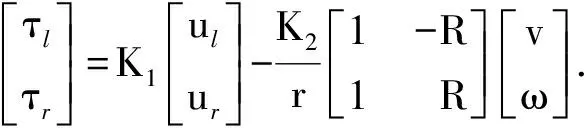
(14)

将式(14)代入式(10),可得联合直流电机的动态模型表达式为

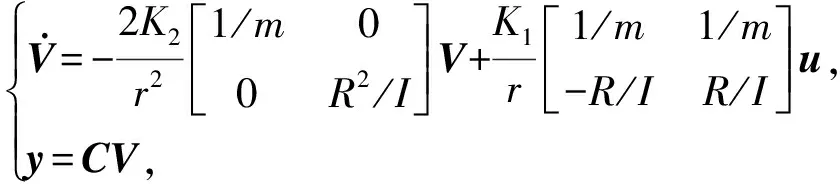
(15)

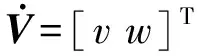
式(15)通过离散化重新整理为

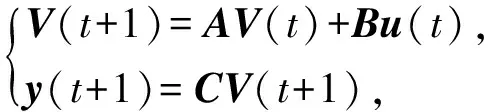
(16)

其中,

重复运行环境中的WMR运动模型可表示为

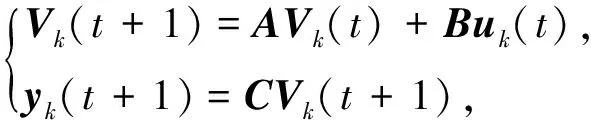
(17)

其中,t∈{0,1,…,N}表示重复的运行区间,N是一个正整数，k∈{0,1,…}表示迭代次数.

注1WMR系统(17)仅用来产生输入输出数据,后续控制器设计及分析均不需要已知A，B和C的信息.也就是说,在本文中A，B和C是未知的.

针对WMR系统(17),本文中给出如下假设:

假设1WMR系统(17)满足相同的初始状态条件,即Vk(0)=c,∀k,其中c为常数向量.

定理1对于非线性系统(17)在满足假设1的条件下,必然存在一个伪雅可比矩阵(Pseudo Jacobian matrix,PJM)Φk(t)使下式成立:

Δyk(t+1)=Φk(t)ΔUk(t),

(18)

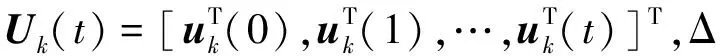
Δyk(t+1)=yk(t+1)-yk-1(t+1),

ΔUk(t)=Uk(t)-Uk-1(t).

证明根据系统(17),可得:

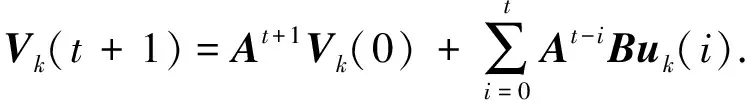
(19)

进一步,系统输出变为

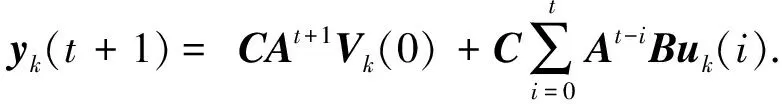
(20)

相邻两次迭代的输出作差,并利用假设1,可得:

Φk(t)ΔUk(t),

(21)

其中,

Φk(t)=[φk(0),φk(1),…,φk(t)],

φk(i)=CAiB,i∈{0,…,t}.

定理1得证.

本文的控制目标是找到一个最优的控制输入使得跟踪误差ek(t+1)=yd(t+1)-yk(t+1)随迭代次数k趋于无穷时收敛于零.

2 控制器设计

考虑如下目标函数:

J(Uk(t),αk)=‖ek(t+1)‖2+

(22)

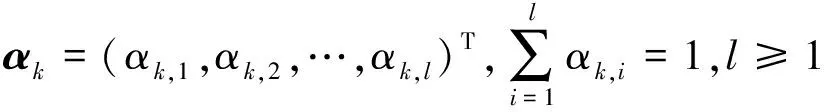
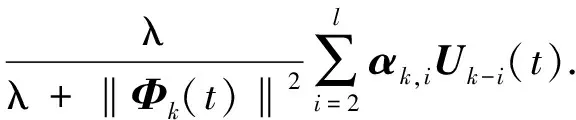
(23)

由于Φk(t)是未知的,所以式(23)可重写为

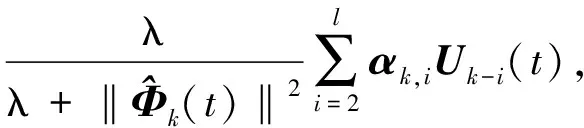
(24)

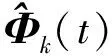
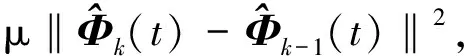
(25)

其中,μ是一个权重因子.

(26)

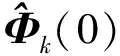
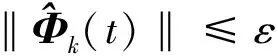
(27)

其中,ε是一个充分小的正的常数.

进一步,为了提高控制算法的对外部扰动的鲁棒性,设计控制律为

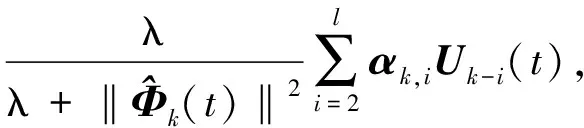
(28)

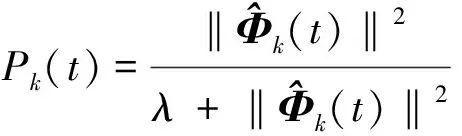
综上所述,所设计的基于数据驱动的高阶学习方案由式(26)、(27)和(28)组成．

从上述控制方案中可以看出,所提的高阶学习方案与MWR的数学模型、机理和阶数均无关.控制方案中只有PJM需要在线调整,与以往数据驱动的自适应ILC方法相比,本文所提方法利用了更多之前迭代的输入信息,提高了控制性能.

3 仿真验证

为了充分说明所提出方法的有效性，本部分给出了仿真验证.

WMR控制系统的参数给出如下:

m=36 kg,I=15.625 kg·m2,2R=1.5 m,r=0.15 m,K1=7.2,K2=2.592.

系统重复运行80次.在仿真中,期望路径设置为

t∈{0,1,…,10}.

为了模拟实际中的外部扰动,在仿真中考虑如下输出扰动dk(t)=[dk,1(t)dk,2(t)]=0.03 rand[1 1],如图2和图3所示.

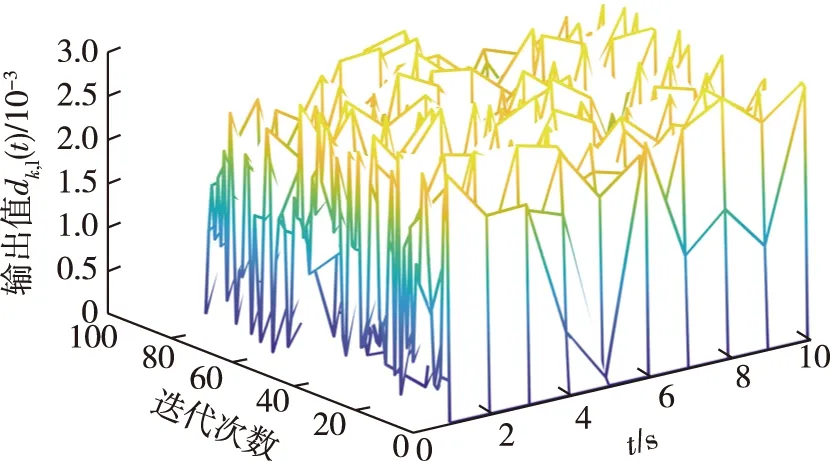
图2 随机噪声dk,1(t)Fig.2 Random noise dk,1(t)

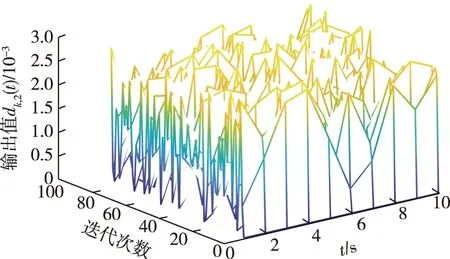
图3 随机噪声dk,2(t)Fig.3 Random noise dk,2(t)

应用本文所提出的基于数据驱动的高阶学习算法(26)—(28),控制器参数设置为η=1,μ=1,ρ=0.2,λ=0.01,l=3,a1=0.1,a2=0.1,a3=0.8,采样时间设置为h=0.1.图4和图5分别表示不同迭代次数下的线速度和角速度的跟踪性能.图6和图7分别表示线速度和角速度的跟踪误差随着迭代的变化情况.从图4—7可以看出所提的基于数据驱动的高阶算法对WVR系统可以达到很好的跟踪控制效果.

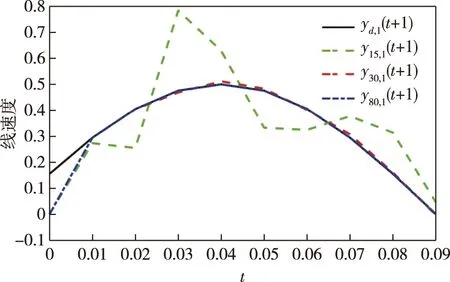
图4 线速度跟踪性能Fig.4 Performance of linear velocity tracking

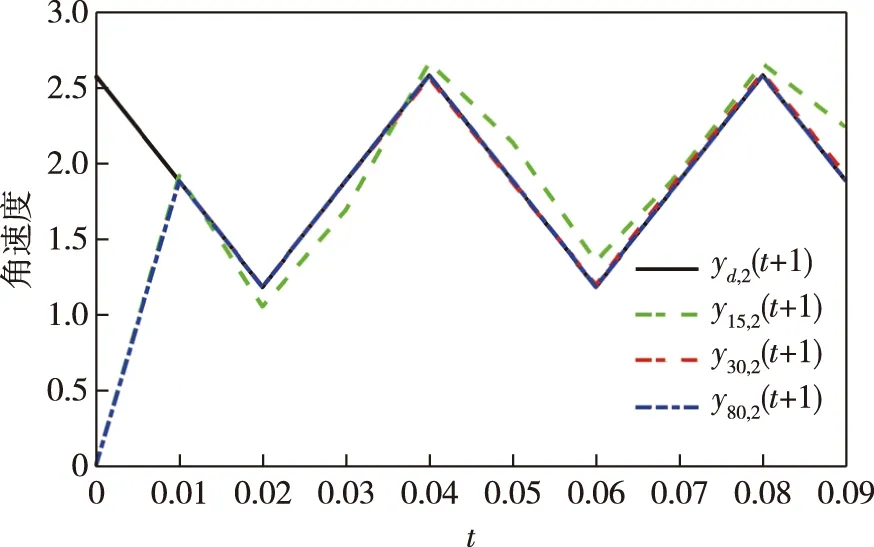
图5 角速度跟踪性能Fig.5 Performance of angular velocity tracking

图6 线速度跟踪误差Fig.6 Tracking error of linear velocity

图7 角速度跟踪误差Fig.7 Tracking error of angular velocity

4 结论

针对轮式机器人执行巡逻任务的重复特性,提出了一种数据驱动的高阶迭代学习控制算法.通过引入基于状态转移的迭代动态线性化技术,将轮式移动机器人系统转化为线性输入输出数据模型形式,在此基础上,利用包含更多之前迭代输入信息的指标函数,设计高阶学习律,并对数据模型中的参数设计更新算法,从而实现轨迹跟踪的目的,提高了控制性能.