基于双幂次滑模的多机器人编队控制
2021-03-31李天龙柏建军
李天龙 柏建军
0 引言
从20世纪70年代到现在,机器人技术作为一个新兴的研究热点,得到了广大学者的关注[1].轮式移动机器人由于其移动灵活、适应性强,具有强大的自身承载能力等优点,已在航空航天、工业生产、物流运输等领域得到了广泛的应用[2].然而,随着需要机器人解决的问题越来越复杂,对机器人的性能提出了更高的要求,甚至出现了某些任务靠单个机器人是无法完成的情况.为了解决该问题,人们开始考虑用多个廉价、功能简单的机器人合作去完成一项复杂繁重的任务.多机器人编队控制作为机器人协同控制的一个重要研究方向,得到了广泛的研究并取得了许多有意义的成果[3-6].
根据控制策略的不同,现有的编队控制方法主要有领航跟随法、虚拟结构法、基于行为法[7]等.相比于其他方法,领航跟随法具有鲁棒性强,能够很好地对系统稳定性进行理论分析等优点,并因此得到了广泛的关注[8].文献[9]基于领航跟随法研究了基于视觉的编队算法,并对队形变换问题进行了探讨;文献[10]研究了具有输入饱和约束下的编队控制问题;文献[11]给出了沿直线编队行进的控制算法,去除了角速度不能为零的限制;文献[12]通过构造新的状态观测器,给出了一种基于视觉的自适应编队控制算法;文献[13]则将滑模控制应用到了船舶的编队控制中,有效地解决了模型不确定与外界干扰对系统性能的影响.
随着滑模控制理论的不断发展,许多学者提出了基于幂次趋近律的滑模控制算法[14-17],有效地解决了传统滑模控制中收敛速度慢、抖震等问题.然而,该方法在编队控制中还少有研究.因此,本文基于双幂次趋近律的滑模控制与领航跟随编队方法相结合,给出了一种能够快速收敛的多机器人编队控制算法.
1 领航-跟随编队模型
移动机器人的结构模型如图1所示.以地面为参考系建立全局坐标系XOY,以移动机器人为参考系建立移动机器人坐标系xoy.图1中2l为y轴方向两个驱动轮之间的距离,2r为驱动轮直径,a为驱动轮轴线中点,d为移动机器人质心o与a在x轴方向的距离,θ为移动机器人行驶方向与水平方向的夹角,因此移动机器人的位姿坐标可表示为[x,y,θ]T.
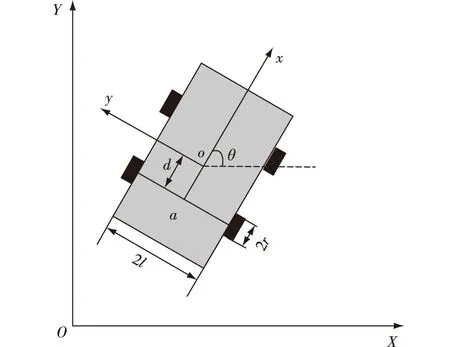
图1 移动机器人的结构模型 Fig.1 Structure of the wheeled mobile robot
该移动机器人的运动学方程为
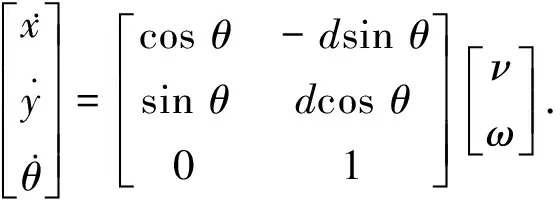
(1)
领航-跟随编队结构模型如图2所示.
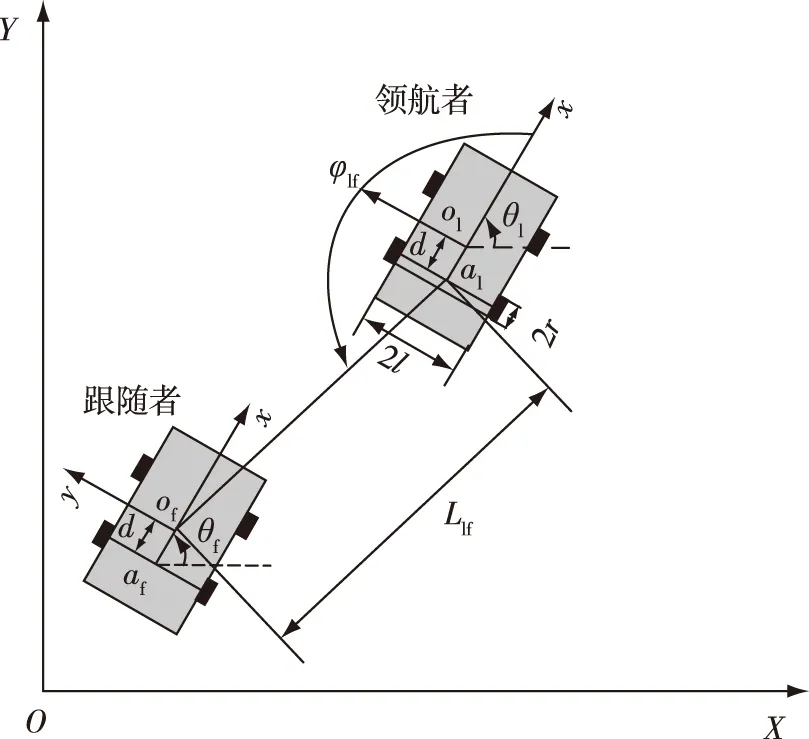
图2 领航-跟随编队结构模型示意Fig.2 Structure of the leader-follower formation
在全局坐标系XOY中,定义领航者的位姿为[xl,yl,θl]T,即质心ol的坐标,第i(i为跟随者的编号,i=1,2,…,n)个跟随者的位姿为[xfi,yfi,θfi]T,即质心ofi的坐标.其中,θl,θfi分别为领航者和第i个跟随者的航向角.以移动机器人的质心ol,ofi作为参考点,Llfi为第i个跟随者参考点ofi与领航者驱动轮轴中心点al之间的距离,即编队之间应该保持的距离.φlfi为领航者航向角与两机器人之间约束距离连线的夹角,称为相对相角.以领航者与第i个跟随者之间的相对相角φlfi和位置距离Llfi来约束编队.每个机器人通过自身携带的传感器以及借助外界传感器获取自身的位姿,跟随者通过无线通信获取领航者的位姿并根据领航-跟随编队控制算法计算出期望跟随者的位姿, 第i个跟随者在控制律的作用下跟踪期望的跟随位置[xrfi,yrfi,θrfi]T,最终第i个跟随者的实际位置与期望跟随位置之间的误差缩减到零,形成期望的编队.综上可计算第i个跟随者的位置为
(2)
其中,
(3)
令
xlfi=xl-dcosθl-xfi=-Llficos(φlfi+θl),
(4)
ylfi=yl-dsinθl-yfi=-Llfisin(φlfi+θl),
(5)
并且分别对式(4)、(5)求导得:
νlcosθl+dωfisinθfi-νficosθfi,
(6)
其中,νl为领航者的前进速度,νfi为第i个跟随者的前进速度,ωfi为第i个跟随者的角速度.
νlsinθl-dωficosθfi-νfisinθfi.
(7)
领航者与第i个跟随者之间的相对相角
(8)
对式(8)求导可得:
dωficos(φlfi+θl-θfi))-ωl.
(9)
对式(3)求导并且代入式(4)—(8)得:
dωfisin(φlfi+θl-θfi).
(10)
因此可以得出领航-跟随编队控制模型为
(11)
第i个跟随者实际位姿与期望参考位姿之间的误差方程[18]定义为
(12)
对式(12)求导得:
(13)
其中,Lrlfi为第i个跟随者参考点ofi与领航者驱动轮轴中心点之间期望的参考距离,φrlfi为领航者与第i个跟随者之间期望的参考相对相角.
2 多机器人编队滑模控制器设计
基于双幂次滑模趋近律,本节设计了编队控制算法,保证了编队队形的稳定.主要结果如下:
定理1对于第i个跟随者的实际位姿与期望参考位姿之间的误差方程(13),线速度控制器(14)和角速度控制器(15)能够保证跟踪误差收敛到零.
νfi=νlcos(θl-θfi)+yefiωfi-
ωlLrlfisin(φrlfi+θl-θfi)+
(14)
(15)
其中:αf11,αf12,αf21,αf22>0;pf11
证明选取如下滑模面:
sf1=xefi,
(16)
sf2=θefi+arctan(νlyefi),
(17)
分别对式(16)、(17)求导并将式(14)、(15)代入得:
yefiωfi-ωlLrlfisin(φrlfi+θl-θfi)=
(18)
(19)
满足如下双幂次趋近律:
(20)
(21)
选取李雅普诺夫函数
(22)
求导并代入式(20)、(21)可得:
(23)
由李雅普诺夫稳定性理论可知,跟踪误差收敛到零,从而保证了编队控制系统渐近稳定.
3 仿真结果及分析
本节通过仿真来验证本文给出的编队控制算法的有效性.不失一般性,考虑两个移动机器人进行编队的情况.领航者初始位姿为[3,4,0.2]T,跟随者初始位姿为[2,2.5,0.5]T,d=0.25 m,给定领航者的参考速度νr=2 m/s ,参考角速度ωr=0.3 rad/s,跟随者参考点of与领航者驱动轮轴中心点之间期望的参考距离Lrlf=1 m, 领航者与跟随者之间期望的参考相对相角φrlf=150°.控制器参数选取为αf11=4,αf12=12,αf21=4,αf22=12,pf11=3,pf12=15,qf11=15,qf12=5,pf21=3,pf22=15,qf21=15,qf22=5.
系统轨迹如图3所示,跟随者可以在较短的时间内到达期望位置并保持稳定的编队结构.跟随者的线速度、角速度分别如图4和图5所示,可知,跟随者的线速度和角速度也都在很短的时间内跟踪到领航者的速度.
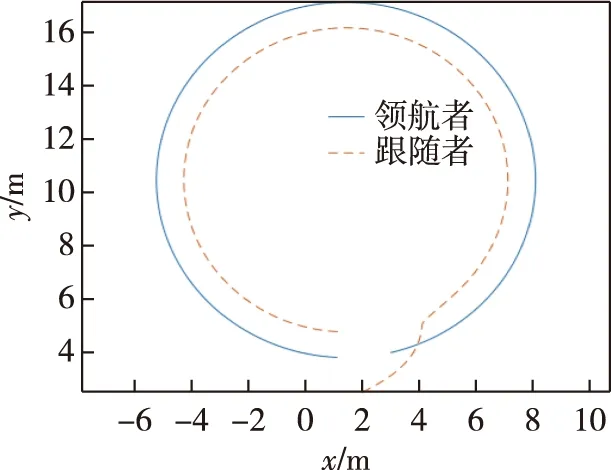
图3 领航者与跟随者编队轨迹Fig.3 Trajectories of the leader and follower

图4 跟随者跟踪领航者速度曲线Fig.4 Velocities of the leader and follower
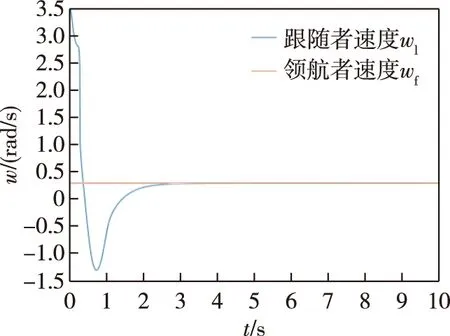
图5 跟随者跟踪领航者角速度曲线Fig.5 Angular velocities of the leader and follower
4 总结
本文研究了轮式移动机器人的编队控制问题.基于领航跟随法,将编队控制问题转化为多个跟随者的轨迹跟踪控制问题.在此基础上,基于双幂次滑模趋近律,设计了跟随者的线速度和角速度控制器,保证了跟踪能够快速收敛到零,从而保证了编队队形的稳定.最后,通过仿真验证了本文所提方法的有效性.
