基于扩张观测器的航天器无速度旋量信息姿轨一体化控制

范睿超 孔宪仁 胡文坤 钟智雄

0 引言

随着航天技术的快速发展,小推力推进技术的日益成熟,以及航天器空间在轨服务、交会对接、高精度观测等复杂航天任务的相继出现,对航天器动力学建模以及控制系统设计等问题提出了更严苛的要求．航天器姿轨一体化建模与控制策略充分考虑了航天器姿轨耦合动力学特性,可以实现姿态以及轨道的同步控制,并能够保证更优良的控制精度、更强的机动性能和更高的控制效率,因此受到了国内外学者的广泛关注[1-4]．特别是基于对偶四元数建立的航天器姿轨一体动力学模型,具有形式简洁、结构紧凑、清晰明了等优势,近年来越来越多的学者进行了深入研究,并且已产出了丰富的理论成果[6-11]．

另一方面,从实际工程角度出发,受到航天器成本、体积、质量、可靠性以及技术的限制,或者由于测量元件的故障、失效等情况,很多航天器的速度信息都无法精确测得,所以在角/线速度信息未知的情况下进行航天器姿轨控制器的设计具有很大的工程意义．目前针对速度信息缺失问题的航天器控制方式主要有三种:一种是利用卡尔曼滤波及其衍生算法对速度信息进行估计,而后利用估计的速度进行控制器的设计[12-14],但卡尔曼滤波器具有计算量较大、参数选取无固定方法、观测状态的收敛性无法严格论证等缺陷,限制了其在高精度速度估计方面的进一步应用;第二种方法是结合无源理论设计无需速度信息的输出反馈控制器[15-17],但控制系统收敛速度较慢,难以在较短的时间内到达期望状态,且对外界干扰的鲁棒性较差;第三种也是最为常用的方式为利用已知的航天器状态信息设计基于模型的状态观测器,再基于该观测器设计航天器姿轨控制器,这种状态观测器因其较快的收敛速度、较高的收敛精度而得到广泛的应用,特别是针对无角速度的航天器姿态控制问题有着较为完善的研究成果[18-23]．值得注意的是,目前已存在的文献中,大量的研究均是围绕无角速度的航天器姿态控制问题,而针对速度信息缺失下航天器姿轨一体化控制器设计的相关研究虽然也取得了一定的进展[24-31],但同时考虑了模型参数不确定性、外界干扰等因素的研究成果较少．

本文针对航天器在轨运行期间由于测量装置故障等原因导致无法精确获得速度旋量信息的情况,基于对偶四元数建立航天器姿轨一体化模型,考虑模型参数不确定性与外界干扰的影响因素,设计了扩张状态观测器并基于Lyapunov稳定性定理分析了观测器观测误差的有限时间收敛性；接着基于该扩张观测器,设计了航天器姿轨一体快速终端滑模控制器,并论证了该控制系统的有限时间收敛性；最后通过数值仿真,验证了该观测器与控制器的有效性．

1 航天器姿轨一体化动力学模型

本节给出基于对偶四元数的航天器姿轨一体化动力学建模．为便于描述,首先给出对偶数、旋量与对偶四元数的运算规则．

其中,四元数Q=[q0qT]T与Qi=[qi0qiT]T的对数运算与乘法运算分别如下:

Q1∘Q2=[q10q20-q1·q2(q10q2+q20q1+q1×q2)T]T,

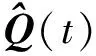
此时,航天器姿轨一体化误差动力学方程可如下表示:

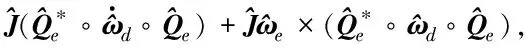
(1)

2 扩张状态观测器设计

本节针对无速度旋量信息反馈的问题,同时考虑模型参数误差与外界扰动,设计扩张状态观测器．

可得如下方程组:

(2)

其中

(3)

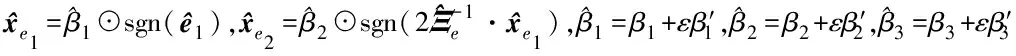
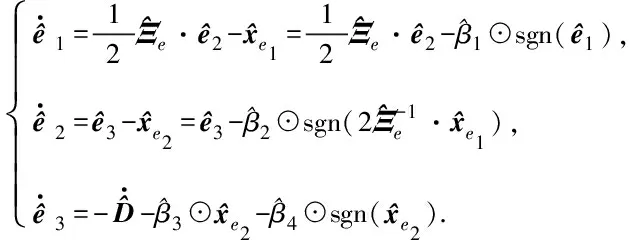
(4)

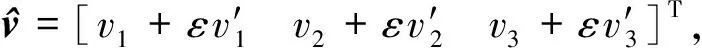
其中

但由于仿真过程中容易产生控制器的抖振,影响控制性能与控制效率,因此在仿真中由饱和函数sat(·)代替符号函数．其中δ为一个充分小的正数．

(5)

其中

证明

选取如式(6)所示Lyapunov函数:

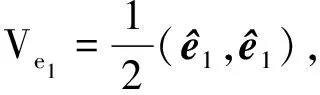
(6)

则其关于时间的导数

(7)

假设

则可知

-(β1-l1)‖e1‖-(β′1-l′1)‖e′1‖.

(8)

-(β1-l1)‖e1‖-(β′1-l′1)‖e′1‖+

(β1-l1)‖e1‖+(β′1-l′1)‖e′1‖=0.

(9)

(10)

选取如式(11)所示Lyapunov函数:

(11)

则其导数为

(12)

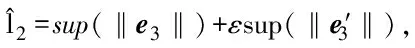
(13)

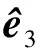
(14)

选取如式(15)所示Lyapunov函数:

(15)

则其导数为

(16)

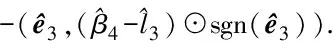
(17)

3 基于扩张观测器的航天器姿轨一体化终端滑模控制

设如式(18)所示快速终端滑模面:

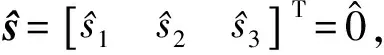
(18)

设计如式(19)所示控制器:

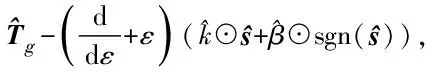
(19)

ε(z′2-z2×Γ′e).

证明

同理控制器(19)可写作:

选取Lyapunov函数如下:

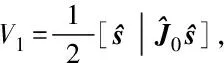
(20)

其导数为

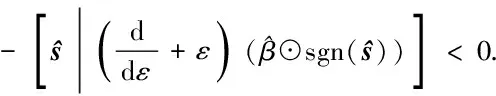
(21)

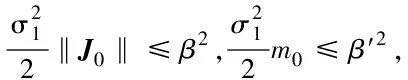
系统状态可在观测器收敛后有限时间内到达滑模面,记Te=Te1+Te2+Te3,则到达滑模面时间为

接下来证明控制系统可在抵达滑模面后有限时间内抵达期望状态．选取如式(22)的Lyapunov函数:

(22)

其导数为

记σ2=min{2λ2i,2λ′2i},i∈{1,2,3},有

因此可得结论,系统到达滑模面之后,系统在有限时间T2内即可到达期望状态:

综上所述,基于扩张观测器(3)的控制系统可在有限时间Te+T1+T2内收敛．

4 仿真分析

为验证如式(3)所示观测器与式(19)所示航天器姿轨一体化控制器的有效性,本节进行该航天器系统的数值仿真验证．如表1所示为航天器目标轨道的轨道根数．初始真近点角θ(0)=0°．

表1 航天器目标轨道根数

航天器受环境干扰力与干扰力矩分别为

设初始状态误差为

观测器参数与控制器参数设置如下:

考虑实际航天器任务中,控制输入为有限值,因此在仿真中设置

|(fu)|≤1 N，|(τu)|≤0.1 N·m，i∈{1，2，3}.

为使仿真结果展示更为直观,本文直接将对偶四元数与旋量等变量解算、分解为姿态四元数与矢量形式．仿真结果如图1—6所示．

图1 扩张观测器的观测误差实部(上)与对偶部(下))Fig.1 Observation error of ESO (real part (upper) and dual part (lower))

图2 扩张观测器的观测误差实部(上)与对偶部(下))Fig.2 Observation error of ESO (real part (upper) and dual part (lower))

图3 扩张观测器的观测误差实部(上)与对偶部(下))Fig.3 Observation error of ESO (real part (upper) and dual part (lower))

图4 误差四元数(上)与位置误差(下)Fig.4 Error quaternion (upper) and position error (lower)

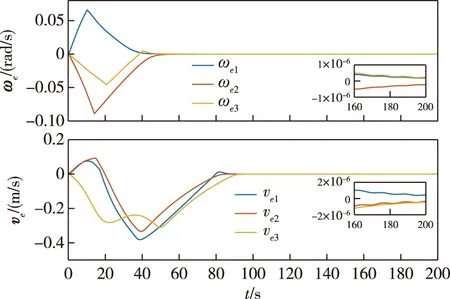
图5 角速度误差(上)与速度误差(下)Fig.5 Angular velocity error (upper) and velocity error (lower)

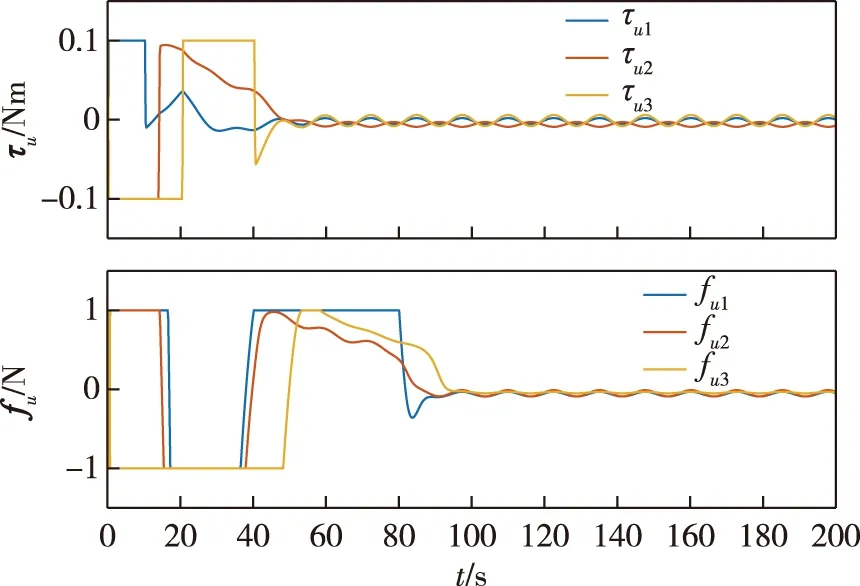
图6 控制力矩(上)与控制力(下)Fig.6 Control torque (upper) and control force (lower)

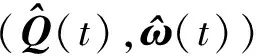
由以上仿真分析可知,本文所设计的扩张状态观测器与航天器姿轨一体快速终端滑模控制器有效解决了在轨运行中航天器速度信息不可知的控制问题,并补偿了由于模型参数不确定性与外界扰动引起的无法测量的干扰因素,使得航天器在速度信息缺失且模型参数存在误差和外界干扰的情况下仍可以充分满足快速、高精度的控制需求,从而验证了本文所设计扩张观测器与快速终端滑模控制器的可行性与有效性．

5 结论

针对航天器在轨运行期间无法获得精确速度旋量信息的情况,考虑存在模型参数不确定与外界干扰的影响,本文设计了基于扩张观测器的航天器无速度旋量信息姿轨一体化控制方法．首先基于对偶四元数建立航天器姿轨一体误差动力学模型,设计了扩张状态观测器,接着基于该扩张观测器设计了航天器姿轨一体快速终端滑模控制器,并利用Lyapunov稳定性定理分析了航天器控制系统的有限时间稳定性．最后通过数值仿真验证了本文所设计扩张观测器与控制策略的可行性与有效性．