社交网络中的谣言传播模型与全局动力学分析

钟晓静 杨宇琨 赵志甲

0 引言

谣言是人类社会交往过程中一种典型的社会现象，它利用各种手段对一个未经证实的事物、事情或问题进行阐述或解释，来吸引公众关注.同时，由于互联网技术的快速发展和移动网络社交平台如Facebook、Twitter、微博和其他社交应用的广泛使用,人们的交流方式也发生了改变.谣言在互联网上传播速度快、范围广，会产生损害个人声誉、影响金融市场稳定、导致社会恐慌和不稳定等问题[1-3].因此，了解在互联网上的谣言传播机制，制定相关措施对谣言进行监督和控制具有非常重要的意义.

谣言传播的动态行为与疾病传播类似但又有区别.相似之处如建模、模型描述和分析问题等，不同之处是传播机制的不同.1964年，Daley等[4]提出了一类经典的DK谣言传播模型，该模型在揭示谣言传播基本规律的同时也指出了谣言传播与疾病传播的区别.1973年，Maki等[5]对DK模型进行修改并提出了MT谣言传播模型.随后，许多研究者对谣言传播进一步研究并取得很多有意义的成果.在建模方面，建立了SIR、SPNR、SEIR等模型[6-8]；在理论分析方面，平均场理论等方法相继被提出[9]；在传播机制方面，犹豫机制、遗忘机制等丰富了谣言传播的研究[10];在网络拓扑结构方面，基于同质网络的谣言传播模型和基于无标度网络的谣言传播模型被提出[11-13].实证研究发现，现实网络中有很多情况符合无标度网络的特性，如社会网络、生物网络、信息网络等.因此，无标度网络的研究已成谣言传播的研究热点.

虽然上述模型对谣言传播的研究做出了贡献，但是它们没有考虑在社交网络中人群的评论对谣言传播的影响.当前网络环境下，弹幕、评论点赞、评论排序等新机制的兴起与流行，谣言的传播方式发生了改变.当一个人在看到他人发布或分享的谣言信息时，他(她)可能会根据自己的理解去评论这个谣言，而评论的个体可能由于看到其他人的评论而变成一个谣言传播者或谣言静默者.同时，谣言在传播过程中，可能受到相关随机因素的影响.

本文将人群细化为无知者(I)、评论者(C)、传播者(S)和静默者(T)四类，提出了一种具有评论机制的ICST谣言传播模型，建立了谣言传播的动力学方程，求出了谣言传播的平衡点，并证明了平衡点的全局稳定性.最后对模型进行了数值模拟，分析了研究结果.

1 谣言传播模型

假设存在一个社交网络，由N个个体构成，个体可以看作网络中的节点，个体之间的关系可以看作是网络节点之间的连边.在整个网络中，人群可以被分成四类:无知者I，不知道谣言但是容易受到影响的群体；评论者C，看到谣言信息并且根据自己的经验和知识去评论谣言信息的群体；传播者S，相信谣言并且传播谣言的群体；静默者T，表示对谣言不感兴趣的群体.为简化模型描述，可以将谣言传播模型写为ICST模型.在社交网络中的谣言传播机制表述如下：

1)假设在单位时间进入网络中的个体为b,每类节点的迁出率为μ.

2)当一个无知者看到一条谣言信息或者接触到一个谣言传播者时，其可能以概率α去评论这条消息变成评论者，α为评论率，或者以概率β分享这条信息变为传播者,β为分享率.

3)当评论者再次看到谣言信息时，可能因为谣言的吸引性会以概率η转变成传播者，或者由于谣言的失真性以概率γ转变为静默者.当传播者再次看到谣言信息时，可能会因对谣言的兴趣减弱而以概率为δ转变成静默者.

基于上述谣言动力学传播机制，各状态间的转移关系如图1所示，其所有参数为正.令Ik(t),Ck(t),Sk(t),Tk(t)分别是度为k的无知者、评论者、传播者、静默者的概率密度随时间t的变化关系.

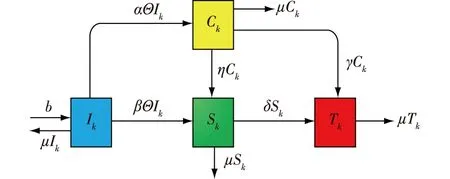
图1 状态转移图Fig.1 State transfer in rumor spreading model

通过以上假设，ICST谣言传播模型动力学方程为

(1)

其中Θ(t)代表在时间t时一个无知者连接到传播者的概率,满足：

节点度为k的总人群Nk(t)满足：

N′k(t)=b-μNk(t).

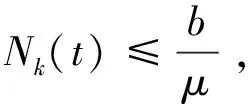
假设网络中迁入个体数量等于迁出个体数量，即b=μ,则I(t)+C(t)+S(t)+T(t)=1.

2 平衡点存在性

谣言传播模型的动力学分析中，首先需要确认的是平衡点的存在性，包括没有谣言和存在谣言两个大的分类.对于具体的平衡点的个数和存在条件，本文给出下述定理.

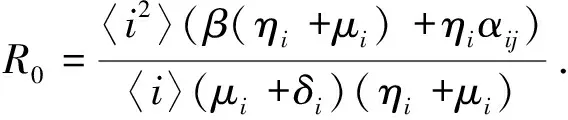
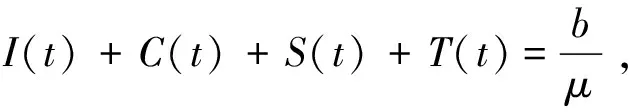
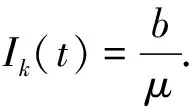
可先假设Θ*为已知量，联立上述方程组可得：

f(Θ*)=

观察上述表达式，Θ*=0时等式成立.但根据Θ*的定理，Θ*>0，因此为使等式成立,函数f(Θ*)需满足：

f′(Θ*)|Θ*=0>1，f(1)<1.

通过计算可得：

根据动力学的数学表达式，定义基本再生数为

因此，当R0>1时，系统存在唯一的正平衡点E*.

3 平衡点稳定性

谣言传播模型平衡点的局部稳定性问题，可通过下一代矩阵方法证明[14]，但平衡点的全局稳定性，需要李雅普诺夫第二方法证明.接下来就设计不同的李雅普诺夫函数证明平衡点的全局稳定性.

定理2系统的动力学性质由基本再生数R0决定，确切的：

1) 当R0<1，无谣言平衡点E0全局渐近稳定；

2) 当R0>1，谣言持续流行平衡点E*全局稳定.

证明首先证明无谣言平衡点的全局稳定性.定义李雅普诺夫函数为

求导可得：

分别代入Ck(t)，Sk(t)的微分表达式可得：

βkΘ(t)Ik(t)-δSk(t)-μSk(t)).

由模型解的可行区间可知：

V′1(t)可看作关于Ik(t)的单调递增函数，由比较原理可得:

当R0<1时，V′1(t)=0当且仅当Sk(t)=0，即为无谣言平衡点E0.由拉萨尔不变原理可知，当R0<1时，无谣言平衡点E0是全局稳定的.

其次证明谣言持续流行平衡点的全局稳定性.定义李雅普诺夫函数为

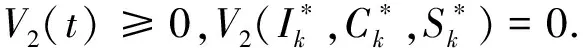
ηCk(t)-(δ+μ)SK(t)],

将持续流行平衡点满足的公式代入上式可组合得到：

再由Θ(t)的定义，最终可以得到：

其中g(x)=x-1-lnx>0，因此

4 仿真

本节通过两个仿真实例观察谣言传播趋势.不失一般性，假设谣言传播所在的网络为无标度网络，分布概率p(k)服从p(k)=2m2k-3，节点度k的变化区间为1≤k≤500，因此可以计算〈k〉=1.368 8.

首先，选取表1第1行中的参数，代入基本再生数R0可知R0=0.135<1，由定理2可得，无谣言平衡点全局稳定.如图2所示，不同节点度的评论者和传播者人群数量均趋于零.为体现全局性特点，选取9组不同的初始条件，如图3所示，最终评论者和传播者的人数均趋于零，这正是说明了解的全局稳定性.

其次，选取表1第2行的系统参数，代入基本再生数计算公式可求得R0=2.43>1.根据定理2可知无谣言平衡点不再稳定，谣言持续流行平衡点全局稳定，图4展示出解均不再趋于零，而是趋于正实数，这表明谣言不会自然灭亡，而是持续传播下去.

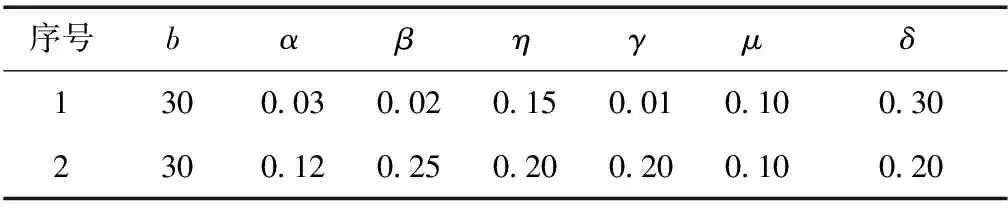
表1 系统参数

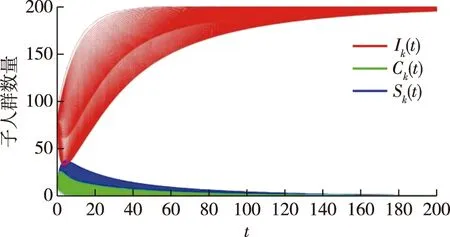
图2 子人群传播趋势(R0<1)Fig.2 Time series of rumor spreading with R0 < 1

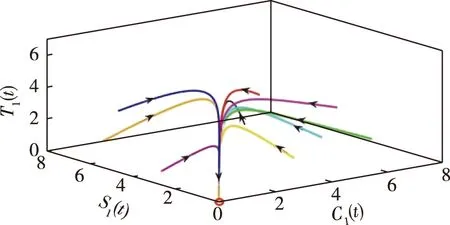
图3 不同初始点出发轨迹Fig.3 Trajectories under nine initial conditions

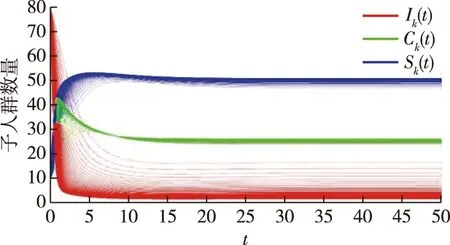
图4 子人群传播趋势(R0>1)Fig.4 Time series of rumor spreading with R0 >1

5 结论

本文以谣言的传播为研究对象，充分考虑人群评论在谣言传播过程中的影响，建立了一类新型的基于社交网络的谣言传播模型.首先证明了平衡点的存在性，在此基础上给出了判断谣言流行与否的阈值;其次，在全局意义上证明了两个平衡点的稳定性.具体的，当R0<1时，无谣言平衡点全局渐近稳定；当R0>1时，无谣言平衡点不稳定，谣言持续流行平衡点全局渐近稳定，这也意味着谣言会持续流行下去.仿真结果表明，基本再生数决定了谣言是自然消亡还是持续流行.