基于执行依赖启发式动态规划的船舶减摇鳍在线最优控制

阮光维 李铁山 于仁海 刘琪

0 引言

当船舶在海上航行时,由波浪、风和海流等外部干扰的影响而产生的横摇运动[1]将极大地减弱船舶的航行效率,船员的日常活动和船舶安全也受到严重影响．因此,在船舶运动控制领域,如何尽可能地减小船舶的横摇动态具有重要意义．在最近的几十年中,随着船舶运动控制技术的不断发展,减摇鳍以其形式小巧、维修简单、减摇效率高等优点被广泛应用于船舶减摇,并且获得了良好的控制性能．然而,该装置的效率取决于控制器设计,控制器的好坏将对减摇鳍系统有很大的影响．因此,减摇控制系统对减摇鳍能否稳定工作有着极其重要的作用．目前,已经有许多控制方法被用来设计船舶减摇鳍控制器．例如:文献[2]提出了一种基于后推技术和闭环增益整形算法的非线性控制器;文献[3]提出了一种PID方法,用于船舶减摇鳍控制器设计,同时基于蒙特卡罗优化技术实现了船舶转向;文献[4]基于非线性扰动观测器,将自适应后推方法应用于非线性船舶横摇系统,并在降低船舶横摇方面获得了较好控制性能;文献[5]提出了一种简化的模糊控制器,用于船舶横摇系统,旨在提高船舶减摇鳍控制器的实时执行效率．

近年来,最优控制已在许多控制领域中得到广泛应用,并成为电机控制、机器人控制等自动控制领域的重要方法之一．在船舶减摇控制领域中,最优控制也有许多相关成果[6-8]．Adaptive Dynamic Programming (ADP)方法是由Miller等[9]提出并广泛应用于控制领域的,其通常在结构上需要三个神经网络,分别是模型网络、评价网络和执行网络．ADP方法的基本思想是通过使用函数近似的结构(模糊模型、神经网络等)来逼近最优控制策略和最优性能指标函数．Miller等[9]介绍了两种ADP结构,分别是双启发式动态规划(DHP)和启发式动态规划(HDP)．后来,随着ADP方法的进一步发展,又有了其他结构,例如执行依赖启发式动态规划(ADHDP)、全局双重启发式动态规划(GDHP)、执行依赖双发式动态规划(ADDHP)、神经网络动态规划结构(NDP)[10]、近似动态规划结构[11]、自适应评价设计结构[12]等．

受Si等[13]和Xiao等[14]的启发,本文提出了一种基于ADHDP(Action Dependent Heuristic Dynamic Programming)方法的新型船舶减摇鳍在线学习最优控制方法．首先对船舶横摇运动模型建立单自由度模型,利用最优控制理论,设计了基于ADHDP方法的船舶减摇鳍控制器．在设计过程中不采用系统模型来获取未来的系统状态值,而直接采用输入输出数据,并使用两个BP神经网络来对最优控制律和性能指标函数进行逼近．评价网络将用于逼近性能指标函数,而执行网络将用于获取最优控制信号．在训练过程中,这两个神经网络不仅可以使用实时测量数据,也可以减少内部模型误差和不确定性干扰的影响,从而提高控制精度和系统的鲁棒性．

本文的其余部分安排如下:第1节提供了船舶横摇系统的线性模型和随机波浪扰动模型;第2节给出了用于船舶横摇系统的ADHDP控制器设计;第3节给出仿真结果;第4节是总结．

1 准备知识和问题表述

1.1 船舶横摇线性模型

在海上航行时,船舶的横摇运动主要是由波浪引起的．当船舶的横摇角度小时,可根据Conolly理论建立船舶线性横摇模型．该模型被广泛用于船舶减摇鳍控制[15],通常描述如下:

(1)

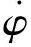
Kc=2Llfcos(α),

(2)

其中L是船的升力系数,由减摇鳍产生,lf是减摇鳍的横摇力臂，α是鳍角度,这是减摇鳍的垂直轴与中心线之间的角度．

将式(1)重新整理得:

(3)

(4)

其中A1,A2,B1是系数,分别表示如下:

(5)

由式(4)得如下状态空间方程:

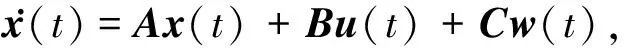
(6)

1.2 波浪干扰模型

本文采用了基于Pierson-Moscowitz谱的波动模型[16],其描述如下:

(7)

其中,H1/3是波高,ωa是波频率,g表示重力加速度．

根据随机过程理论,可将波的倾斜角模型描述如下:

(8)

其中μl表示波倾斜角初始相位,其值在0～2π之间随机变化．为方便计算,本文选择μl=0,则能谱与波高谱之间的关系式为

(9)

其中G1和G2是系数,根据船体的形状而变化．考虑到船舶航速和航向对船舶所遭遇的海浪频率的影响,可以将船舶的所谓相遇频率描述如下:

(10)

其中V是船速,β是海浪的方向．根据能量等价原理,遇到频率能谱密度函数与自然频率能谱密度函数具有以下关系:

(11)

因此实际仿真中的波倾角模型如下:

(12)

使用上述公式进行模拟,当(1-2ωaVcos(β))/g=0时,Sp(ωe)中将会产生断点,因此具有以下关系式:

Sp(ωa)Δωa=Sp(ωe)Δωe.

(13)

将式(13)代入式(12),可得:

(14)

图1所示为随机海浪,其中H1/3=5.8,n=28,波浪方向β=450，船速V=7.8 m/s

图1 随机海浪Fig.1 Random waves

2 船舶减摇鳍系统的ADHDP控制器设计

线性模型(6)可以写成如下的离散时间形式:

x(t+1)=Adx(t)+Bdu(t)+Cdw(t),

(15)

其中x(t)是系统的状态变量,Ad是系统状态矩阵,Bd,Cd是系统的输入矩阵,w(t)表示外部干扰,u(t)用于表示系统的输入信号．本文的任务是设计最优控制器u(t)以最大程度地减少如下的性能指标函数:

(16)

其中γ是性能指标的折扣因子,0<γ≤1．为简单起见,本文中γ=1.函数U(x(i),u(i))=xT(i)Qx(i)+uT(i)Ru(i)是效用函数,其中Q是一个半正定矩阵,而R是一个正定矩阵．根据Bellman原理,最优性能指标函数J*(x(t),u(t))可以写成如下形式:

J(x(t+1),u(t+1))),

(17)

该方程也被称为离散时间Hamilton-Jacobi-Bellman(DTHJB)方程.通过最小化性能指标函数,可以得到最优控制策略:

J(x(t+1),u(t+1))).

(18)

ADHDP在结构上需要使用两个神经网络:一个是评价网络用于估计性能指标函数J(x(t),u(t)),另一个是执行网络用于逼近控制信号u(t)．图2为船舶减摇鳍系统最优ADHDP控制器示意图．

图2 船舶减摇鳍系统的ADHDP结构Fig.2 ADHDP structure for ship fin stabilizer system

图2中,实线表示信号流,虚线表示评价网和执行网的参数更新路径．系统的状态变量是执行网的输入,它将输出控制信号u(t)之后,该控制信号与系统的状态变量相结合,成为评价网的输入,它将在(17)中输出目标函数的近似值．u(t)也是减摇鳍系统的控制输入．评价网和执行网是基于BP神经网络的非线性多层反馈网络．下一部分将给出评价网和执行网的详细结构．

2.1 评价网

在ADHDP方法中,本文使用了评价网来逼近性能指标函数J(t)． 这里设计一个3-6-1结构的评价网(图3),其中包含3个输入神经元、6个隐含层神经元和1个输出神经元．输入信号x1,x2是系统的状态(船舶横摇角和船舶横摇角速度),控制信号u(t)从执行网的输出信号中获得．评价网的激活函数采用sigmoid函数,评价网结构如下所示:

(19)

图3 评价网络的结构Fig.3 Structure of critic network

评价网的输出层可以表示为

(20)

其中Ic(t)∈R3×1是输入向量,J(t)是输出向量,hc(t)∈R1×6是隐含层的输出向量,wc1∈R6×3是输入到隐含层的权重向量,wc2∈R1×6是隐含层到输出层的权重向量．

在评价网中,前向过程计算目标函数的近似值,而后向过程则更新评价网的权重矩阵．定义评价网误差函数为

ec(t)=γJ(t)-J(t-1)+U(t)，

(21)

评价网中的目标函数为

(22)

评价网络的权重更新算法基于梯度下降方法,它是通过应用链式规则获得的．输入层到隐含层的权值更新表示为

wc1(t+1)=wc1(t)+Δwc1(t),

(23)

其中Δwc1(t)∈R6×3,

(24)

其中i是矩阵行号,j是矩阵列号,lc>0 是评价网的学习率.

隐含层到输出层的权重向量更新表达式为

wc2(t+1)=wc2(t)+Δwc2(t),

(25)

其中Δwc2(t)∈R1×6,

(26)

其中i是权重矩阵的行数.

注1在式(24)和(26)中,∂Ec(t)/∂J(t)由式(21)和(22)计算,而∂J(t)/∂wc(t)与状态变量和控制输入有关．

2.2 执行网

本文采用执行网获取控制信号u(t),设计了一个2-6-1结构的执行网络(图4),其中包含2个输入神经元、6个隐含层神经元和1个输出神经元． 包括x1,x2的输入信号是系统的状态变量,输出信号是系统的控制信号,同时使用sigmod函数作为激活函数．

图4 执行网络的结构Fig.4 Structure of action network

执行网络的输出信号可以确定为

(27)

其中Ia(t)∈R2×1是输入向量,u(t)是输出向量,ha(t)是隐含层的输出向量,wa1∈R6×2是输入层到隐含层的权重向量,wa2∈R1×6是隐含层到输出层的权重向量.

定义执行网误差函数为

ea(t)=J(t).

(28)

最小化下面的目标函数,以更新执行网络中的权重:

(29)

执行网络的权重更新算法是基于梯度下降方法,通过应用链式规则给出的.如下所示输入层到隐含层的权值更新表示为

wa1(t+1)=wa1(t)+Δwa1(t),

(30)

其中Δwa1(t)∈R6×3,

(31)

其中i是矩阵行数,j是矩阵列数,la>0是执行网的学习率,Hl是执行网中隐藏节点的数量,n是评价网的输入信号的数量．

隐含层到输出层的权重更新表达式为

wa2(t+1)=wa2(t)+Δwa2(t),

(32)

其中Δwa2(t)∈R1×6,

(33)

注2在式(31)和(33)中,∂Ea(t)/∂J(t)由式(28)和(29)计算,而∂J(t)/∂u(t)通过链式规则获得,该规则与执行网中的权重矩阵相关[14]．

3 仿真研究

本节将对容器进行仿真,船舶参数如表1所示．

表1 船舶参数

船舶横摇动态的状态空间方程如下:

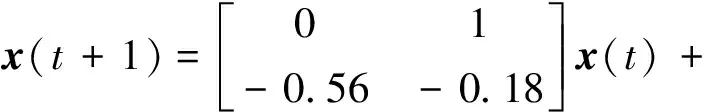
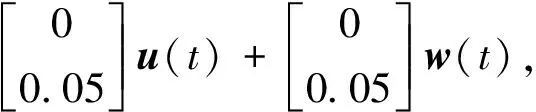
(34)

效用函数可以设计如下:

U(x(i),u(i))=xT(i)Qx(i)+uT(i)Ru(i),

(35)

本文设计了具有两个神经网络的ADHDP控制器,每个神经网络的参数如下:评价网为3-6-1结构,具有3个输入神经元、6个隐含层神经元和1个输出神经元,执行网为2-6-1结构,有2个输入神经元、6个隐含层神经元和1个输出神经元；评价网和执行网的学习率lc=la=0.005；初始权重矩阵wc1∈R6×3和wa1∈R6×2分别为评价网和执行网中输入层到隐含层的权值矩阵,初始权重矩阵wc2∈R1×6和wa2∈R1×6分别为评价网和执行网中的隐含层到输出层的权值矩阵,权值在 [-1,1]中随机选择．初始权重矩阵选择如下:

为了验证所设计控制器的有效性,本文设计了船舶减摇鳍的线性二次调节器控制器来进行比较．线性二次调节器控制器(Linear Quadratic Regulator,LQR)表示如下:

(36)

图5为具有减摇鳍和不具有减摇鳍控制器的船舶横摇角及横摇速率的变化情况．由图5可见,设计的减摇鳍控制器的有效性较好．图6为本文设计的控制器(ADHDP)和线性二次调节器控制器(LQR)的比较,表明本文设计的控制器获得比较好的控制效果．图7和图8分别为评价网络和执行网络的权重收敛过程,显然权重都收敛到常数,这表明所提出的控制器具有很好的性能．

图5 具有减摇鳍和不具有减摇鳍的横摇角和横摇速率的变化情况Fig.5 Roll angle and roll rate with and without fin stabilizer

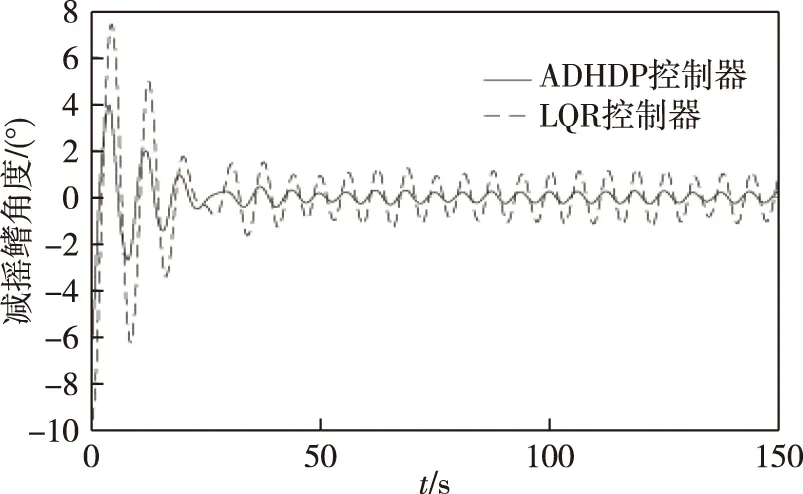
图6 ADHDP和LQR控制器对比Fig.6 Comparison between ADHDP and LQR controller

图7 评价网络的权值矩阵Fig.7 Weight matrices of critic network

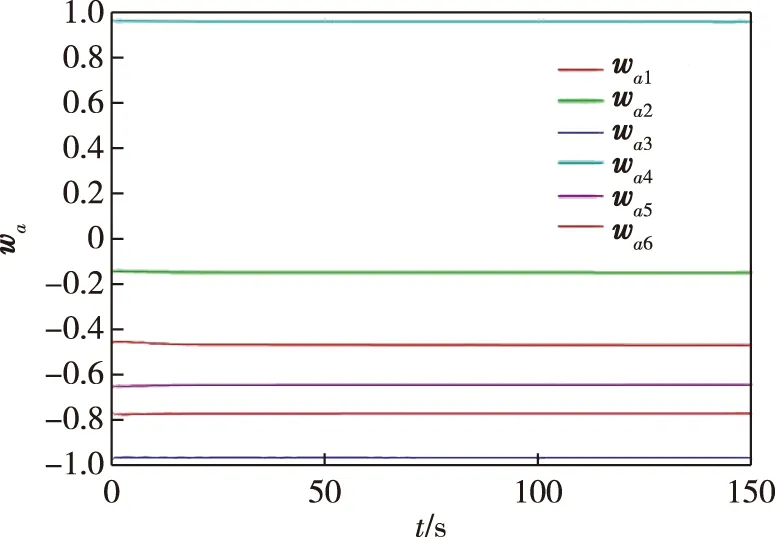
图8 执行网络的权重矩阵Fig.8 Weight matrices of action network

4 结束语

本文提出了一种基于ADHDP方法的船舶减摇鳍系统的最优控制器．本文所提出的方法是利用评价网络来逼近针对船舶减摇鳍控制系统设计的性能指标函数,并通过执行网络来获得最优控制律．ADHDP的优点是在线训练,ADHDP结构中的两个神经网络既可以使用实时测量数据,同时也可以减少内部模型误差和不确定性干扰的影响,从而提高了鲁棒性．仿真结果验证了该方法良好的减摇效果．