超临界态甲烷密度研究

张新宾，宋党育，李云波，齐永安，范顺利

超临界态甲烷密度研究

张新宾1,2，宋党育1,2，李云波1,2，齐永安1,2，范顺利1,2

(1. 河南理工大学 资源环境学院，河南 焦作 454003；2. 中原经济区煤层(页岩)气河南省协同创新中心，河南 焦作 454003)

超临界甲烷密度不仅是非常规天然气资源量计算与吸附能力测定的重要参数，同时也是衡量超临界甲烷扩散效率与溶解有机物能力的主要指标。通过对比分析各种气体状态方程的适用性，认为基于亥姆霍兹能量基本状态方程可以准确计算0~30 MPa、270~360 K条件下甲烷的密度。利用Microsoft Office Excel编写了甲烷密度的计算程序，与NIST(美国国家标准与技术研究院)商业软件计算结果相比，误差小于0.05%。分析了0~100 MPa、270~360 K范围内甲烷密度的变化规律。结果表明，甲烷密度随压力增大而增大，在低于30 MPa时增速较大且对温度的敏感性较强，高于30 MPa时增速逐渐变缓，且敏感性减弱。在煤层原位条件下随着埋深的增大，甲烷密度随温度升高而减小，随压力增大而增大；在温度与压力共同作用下，甲烷密度呈先增速不变、近似线性增加，后增速逐渐减小、凸曲线形增加的变化规律。游离态甲烷密度受温度的影响比吸附态甲烷小，是深部煤层气资源增量的主要贡献者。研究结果为深部煤层气赋存及其潜力预测提供了基础参数。

超临界甲烷；甲烷密度；气体状态方程；亥姆霍兹能量；煤层气资源量

超临界流体是指温度和压力都超过临界点时的流体。经典超临界流体理论认为，超临界流体是结构均匀的单相流体，其蒸发潜热和表面张力消失，不再发生相变，也不存在气液共存界限[1]。严格意义上讲超临界流体既不是液体也不是气体，在有的温压区间内具有气体的高扩散性，有的温压条件下具有液体的溶解性，同时在临界点附近温度或压力的微小变化可能造成密度的急剧改变。因此，密度是判断超临界流体性质的主要依据[2]。

甲烷的临界温度是–82.6℃，临界压力是4.6 MPa，当温度和压力都超过临界值时即为超临界态[3]。在正常地温与压力梯度下，当埋藏深度超过500 m时煤层中的甲烷已达到超临界状态。但是由于储层温度远远超过甲烷的临界温度，当储层压力超过甲烷的超临界压力后，甲烷的密度是否会发生明显变化，超临界态甲烷对煤层的吸附能力会产生哪些影响？前人对这些问题并没有非常明确的认识。严格来说超临界态甲烷的密度及其随压力、温度的变化规律与理想气体明显不同[4]，在深部非常规天然气资源评价中，游离态甲烷资源量的计算需要准确的甲烷密度参数。

1978年，国际纯粹与应用化学联合会(IUPAC)提出了基于状态方程推导超临界甲烷热物性的方法，同时列出了部分温度与压力下甲烷的热力学数据[5]。理想气体状态方程主要是在假设体积不变的情况下推导出密度公式，然而理想气体状态方程无法描述液相区和密度较高的气相区的性质[6]。为得到真实气体的状态方程，可对理想气体状态方程进行修正，数学上最简单的方式是定义压缩因子[7-8]。在甲烷高压等温吸附实验中目前采用固定的温度、压力点下甲烷的压缩系数校正自由体积中的甲烷量[9]，与理想气体状态方程和利用压缩因子得到的真实气体状态方程相比，R-K方程在计算甲烷密度时的应用范围和计算精度方面都有了一定的提高，但其在高压下和预计物质的液相密度时误差较大[10]。如果可以快速计算不同温度、压力下游离态甲烷的密度，可以更加准确地测定煤的吸附能力。目前可以从一些文献中查阅部分压力和温度下甲烷密度，也可以利用一些商业软件计算不同温度和压力下甲烷的密度和其他热力学参数，如ASPEN和REFPROP软件，分别为美国AspenTech公司和NIST(美国国家标准与技术研究院)开发的商业软件。也有学者通过实验测定了不同温度、压力下超临界甲烷密度[11-15]。从行业应用角度而言，需要根据超临界甲烷密度随温度与压力的变化规律，快速计算不同温度、压力下超临界甲烷密度。

论文基于亥姆霍兹能量守恒定律，利用亥姆霍兹能量形式的基本方程，通过将无量纲亥姆霍兹能量分解为理想气体行为和残余流体行为两部分，采用优化经验热力学方程结构的方法，建立了270~360 K、0~30 MPa的温度与压力区间内甲烷密度的计算方法。利用Excel软件，采用迭代法、单变量求解和宏操作，编制了不同温度、压力下超临界甲烷密度的直接计算程序，在此基础上分析超临界甲烷密度随温度与压力的变化规律。

1 特殊区域气体状态方程

在化工和能源技术领域，工艺和设备的设计需要准确的流体热物理参数。然而，由于统计热力学在理论上还没有达到足够的精确与简捷，在大多数情况下人们必须使用经验公式，这些公式是基于覆盖整个流体区域的相应精确实验数据得出的。1989年，U. Setzmann等[16]提出了优化经验热力学方程结构的新思路，在考虑物理依赖性的综合函数表达式，即所谓“数据库”的基础上，同时优化了方程的结构和长度。

特殊区域气体状态方程是基于亥姆霍兹能量形式的基本方程而建立的新状态方程[17]。在热力学中，亥姆霍兹能是一个热力学势，用在恒定的温度和体积下从封闭热力系统能得到最大“有用”功。对于这样一个系统，亥姆霍兹能差值的负数等于温度和体积保持不变下可逆等温过程的最大功输出，即=–。新状态方程采用将其转化为无量纲形式的亥姆霍兹能量=/()，即为无量纲形式的亥姆霍兹能量。可将其分解为理想气体行为o和残余流体行为r两部分：

理想气体部分的无量纲亥姆霍兹能量与经验方程关联：

式(1)中的重点是确定亥姆霍兹能量残余部分的函数形式。首先是建立方程的通用表达式，该表达式起着“数据库”的作用。为了使最终方程尽可能简单，“数据库”以和表示为一个简单的多项式：

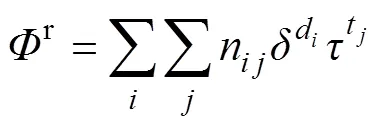
式中：d的范围是1~9，宽度为1；t的范围是–0.5~10，宽度为0.25。

这意味着整个“数据库”包含387个项。然后再根据式(3)，采用一种特殊优化程序确定有限项的最佳组合，将线性优化过程与所有数据(线性和非线性)的非线性拟合迭代组合[18]，最终得到亥姆霍兹能量残余部分的函数形式[17]：

式中：n为方程的系数；d、t为指数。

这样就建成了270~360 K、0~30 MPa条件下的有效状态方程：

wj,k为方差为Q的零均值白噪声序列；ζk为变速因子；Φk为气隙磁量；φu,k∈Φk，为第u个导磁爪与磁极间的气隙磁通量。

与方程推导过程中采用的实验数据集相比，利用特殊区域气体状态方程计算得到的甲烷密度的不确定度为：0＜≤12 MPa时，Δ/≤±0.02%；12＜≤30 MPa时，Δ/≤±0.05%。在范围和精度方面都满足了超临界甲烷密度的计算要求。

2 超临界甲烷密度的计算

考虑到超临界甲烷的温度、压力范围和对密度计算精确度的要求，通过对比文献中不同的状态方程，认为采用亥姆霍兹能量方程与热力学参数的关系式可以更加准确地计算超临界甲烷密度。

2.1 计算方法与过程

根据亥姆霍兹能量方程与热力学参数的关系式，压力与无量纲形式的亥姆霍兹能量具有关系：

对式(4)求偏导得：

联立式(6)、式(7)得：

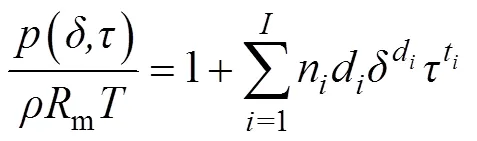
式中：c取值162.66 kg/m3；c取值190.564 K；m为比气体常数，J/(kg·K)。其中m=/，为气体的摩尔质量，g/mol；n、d、t取值见表1。

将对应参数代入式(8)后即可计算得到特定温度和压力下的甲烷密度。

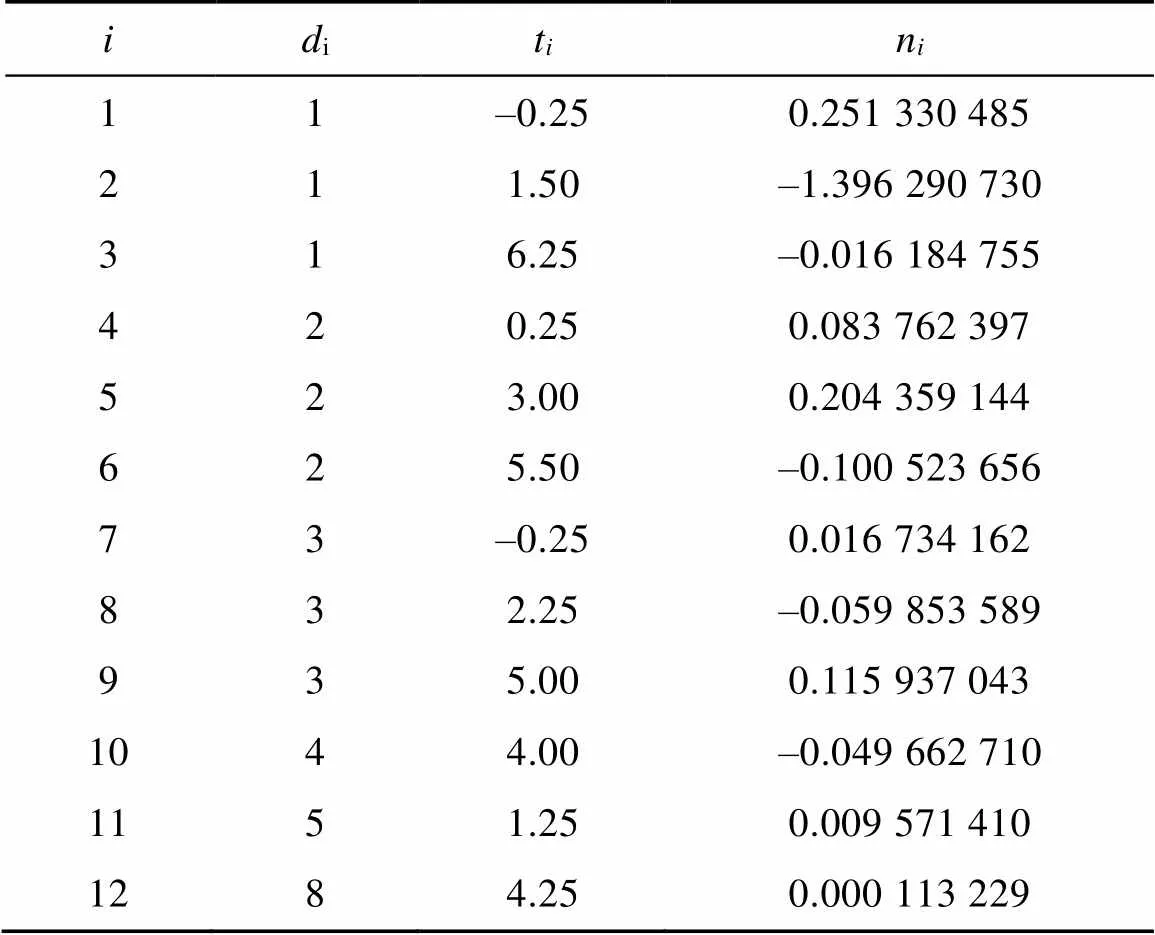
表1 甲烷状态方程中的参数ni、di、ti取值

2.2 计算实现过程

式(8)可转化为一元九次方程。基于阿贝尔定理(即各项系数经过有限次四则运算和乘方与开方运算无法求解5次及以上的一元高次方程)，对于一元九次方程并没有通用的代数解法和求根公式，可以采用迭代法求近似解的方式求解。迭代法也称辗转法，是一种不断用变量旧值递推新值的过程。迭代算法是用计算机解决问题的一种基本方法，利用计算机运算速度快、适合做重复性操作的特点，对一组指令或一定步骤重复执行，在每次执行这组指令或步骤时，都从变量的原值推出一个新值[19]。

为简化计算过程，同时考虑到Microsoft Office Excel(简称Excel)强大的计算能力和便捷性，本文采用其中的单变量求解功能求解方程。在Excel运算中，单变量求解是根据目标值不断调整变量，直至计算结果与目标值无限接近时，才能确定变量值[20]。

将式(8)转化为：

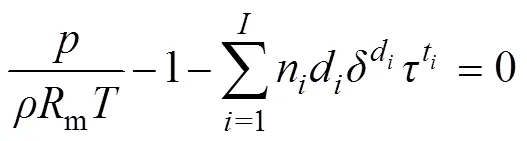
甲烷密度计算方法如图1所示，计算步骤为：①首先，在Excel中输入温度、压力常数与相关计算参数以便方程引用；②选择任一单元格，输入任意数值作为变量密度的初始值；③选择任一单元格输入式(9)，公式必须引用密度的初始值；④设置迭代计算参数，如迭代次数和最大误差；⑤选择单变量求解功能，在目标单元格中引用输入公式的单元格，并将目标值设置为0，在可变单元格编辑框中引用输入变量密度的单元格，即可实现自动迭代计算。当迭代次数达到设置次数或者目标值误差小于设置误差时计算结束。当计算结束时，此时密度变量单元格的最新数值便是甲烷密度值。

为简化操作过程，将一系列操作过程录制为宏并设置控件。若要获得指定温度和压力下的甲烷密度，只需在输入框中输入温度和压力，计算机便会在自动运行一系列程序后将甲烷密度的计算结果直接显示在输出框中。

图1 超临界甲烷密度计算方法演示界面

2.3 结果误差分析

为检验本方法计算结果的准确性，计算得到0~30 MPa，270、300、330、360 K四个温度下的甲烷密度，以NIST商业软件的计算结果为参考值进行误差分析，结果如图2所示。相对误差=(m–n)/n，其中，n为NIST软件计算的甲烷密度，m为本文计算得出的甲烷密度。

由图2可知，各个温度下随着压力的增大误差都呈现上下波动的趋势，误差绝对值总体小于0.05%。在压力为18 MPa之前，各个温度下的误差都较小，均小于0.012 5%；在18 MPa之后，各个温度下的误差都有所增大，其中，270 K温度下误差最大，但最大误差都不超过0.05%。

3 甲烷密度的变化规律

为了分析不同温度、压力下甲烷的密度变化特征，采用本论文方法计算得出0~30 MPa，270、300、330和360 K 4个温度下的甲烷密度(图3中红色虚线左侧)，同时利用NIST得到30~100 MPa下相应温度的甲烷密度(图3中红色虚线右侧)，结果如图3所示。

图2 不同压力、温度下本文方法计算的密度值与NIST方法计算的密度值之间的误差

由甲烷密度随压力的变化曲线(图3a)可以看出，随着压力的增大，各个温度下的甲烷密度都呈现单调增加的趋势，且随压力升高密度增加幅度越来越低。在临界压力(4.6 MPa)前后，密度没有明显的突变；在0~100 MPa、270~360 K范围内温度对密度的影响远远小于压力，随着压力的增大，不同温度间的甲烷密度差异呈现先增大后减小的趋势，在约30 MPa时密度差异最大而后开始减小(图3a)。由图3b可以看出，在低压阶段(约30 MPa之前)温度对甲烷密度的影响较为显著，随压力升高，温度越低密度增加的速度越快，高压阶段(约30 MPa之后)不同温度下密度随压力增加的幅度趋于相近。甲烷密度增量的变化规律以30 MPa为界大致分为两个阶段(图3b)：在30 MPa之前，密度增量随压力增大呈先增加后减小的抛物线形，且温度越低密度增加幅度越大；在30 MPa之后，随压力升高甲烷密度增量继续减小，温度越低密度增量减小幅度越大。

图3 不同温度、压力下的甲烷密度和密度增量

参考华北盆地的平均地温梯度与正常储层压力梯度[21-24]，得到埋深在100~3 000 m范围内的温度和压力分别为289.7~363.0 K、1~30 MPa，同时计算不同埋深对应的温度和压力下的甲烷密度，如图4所示。

由图4可知，随着煤层埋藏深度逐渐增加，煤层压力与温度逐渐增大，甲烷密度在1 500 m以浅呈近线性增加，深度超过1 500 m以后增加幅度逐渐变缓。密度的变化同时受控于温度与压力，压力增大使密度升高，温度升高使密度降低，温度与压力的双重作用导致密度随埋深增加出现先呈近线性增加而后增幅变缓的变化规律。在埋藏深度增加的过程中，对密度的变化起主导作用的是压力，但是随埋深增加，压力的影响逐渐变弱。

由甲烷密度随埋藏深度的变化规律可知，随煤层埋深的增加，游离态甲烷的资源量逐渐增加。例如2 000 m埋深处甲烷的密度是500 m埋深的3.6倍，即假设煤层孔隙率不变，游离态资源量增加2.6倍。煤层对甲烷的吸附能力同样受温度、压力双重因素控制，埋藏深度超过1 000 m以后温度对吸附量的影响超过压力，从而出现吸附量降低的转换带[25]。所以煤层埋深超过1 000 m以后对资源量增量的贡献主要来源于密度增加的游离态甲烷，这种效应在以游离态为主的页岩气中尤为明显。在埋藏深度超过2 000 m以后，随深度继续增加，游离态甲烷密度增加幅度变缓，对资源量增加的贡献变弱。

图4 不同埋深下甲烷密度随温度、压力的变化关系

4 结论

a. 基于亥姆霍兹能量基本方程的经验状态方程可以描述超临界甲烷的热力学行为，利用Microsoft Office Excel编写的超临界甲烷密度计算程序计算得出的270~360 K、0~30 MPa温度与压力范围内的甲烷密度，其准确度符合要求。此方法程序准确便捷，可以与煤的高压甲烷等温吸附实验数据计算程序相结合，更加准确地计算储层条件下游离态甲烷资源量和煤层中超临界甲烷的吸附能力。

b. 在270~360 K、0~100 MPa条件下，甲烷的密度随着压力的增大呈现单调增加的趋势，密度随压力增加的速率在30 MPa时出现拐点，高于30 MPa后不仅甲烷密度增加缓慢，同时密度对温度的敏感性出现反转，在30 MPa前温度越低密度随压力的增量越大，在高于30 MPa后温度越低密度随压力的增量越小。

c. 在平均地温梯度与正常储层压力梯度下，随煤层埋藏深度的增加，甲烷密度在约1 500 m以浅呈现近线性增加，而后随埋深增加密度增加幅度逐渐变缓。与吸附态相比，游离态甲烷受温度的影响较小，游离态甲烷资源量是深部煤层气资源增量的主要贡献者。

[1] BANUTI D T. Crossing the widom-line-supercritical pseudo- boiling[J]. The Journal of Supercritical Fluids，2015，98：12–16.

[2] 王艳，徐进良，李文，等. 超临界流体密度波动机理的分子动力学模拟[J]. 科学通报，2020，65(17)：1694–1704. WANG Yan，XU Jinliang，LI Wen，et al.Molecular dynamics study of mechanism of density fluctuation in supercritical fluid(in Chinese)[J]. Chinese Science Bulletin，2020，65(17)：1694–1704.

[3] 周理，李明，周亚平. 超临界甲烷在高表面活性炭上的吸附测量及其理论分析[J]. 中国科学：B辑，2000，30(1)：49–56. ZHOU Li，LI Ming，ZHOU Yaping. Adsorption measurement and theoretical analysis of supercritical methane on high surface activated carbon[J]. Science in China(Series B)，2000，30(1)：49–56.

[4] 梁洪彬，戚志林，向祖平，等. 超临界页岩气密度特征研究[J]. 油气藏评价与开发，2017，7(5)：74–79. LIANG Hongbin，QI Zhilin，XIANG Zuping，et al.Research on the characteristics of the density of supercritical shale gas[J]. Reservoir Evaluation and Development，2017，7(5)：74–79.

[5] ANGUS S，ARMSTRONG B，De REUCK K M. International thermodynamic tables of fluid state methane[M]. Oxford：International Union of Pure and Applied Chemistry，1978.

[6] 童景山. 化工热力学[M]. 北京：清华大学出版社，1995. TONG Jingshan. Chemical engineering thermodyna-miss[M]. Beijing：Tsinghua University Press，1995.

[7] 杨兆彪，秦勇，高弟，等. 超临界条件下煤层甲烷视吸附量、真实吸附量的差异及其地质意义[J]. 天然气工业，2011，31(4)：13–16. YANG Zhaobiao，QIN Yong，GAO Di，et al.Differences between apparent and true adsorption quantity of coalbed methane under supercritical conditions and their geological significance[J]. Natural Gas Industry，2011，31(4)：13–16.

[8] 孙红明，傅雪海，丁永明，等. 煤层气压缩因子解析计算模型的建立[J]. 新疆石油地质，2014，35(2)：215–220. SUN Hongming，FU Xuehai，DING Yongming，et al.Analytical calculation model for coalbed methane compressibility factor[J]. Xinjiang Petroleum Geology，2014，35(2)：215–220.

[9] 中国国家标准化管理委员会. 煤的高压等温吸附实验方法：GB/T 19560—2004[S]. 北京：中国标准出版社，2008. China National Standardization Management Committee. Experimental method of high-pressure isothermal adsorption to coal：GB/T 19560—2004[S]. Beijing：Standards Press of China，2008.

[10] 时钧，汪家鼎，余国琮，等. 化学工程手册(第二版)上册[M]. 北京：化学工业出版社，1996. SHI Jun，WANG Jiading，YU Guocong，et al. Chemical engineering handbook(2rdEdition)[M]. Beijing：Chemical Industry Press，1996.

[11] ACHTERMANN H J，BOSE T K，ROGENER H，et al. Precise determination of the compressibility factor of methane，nitrogen，and their mixtures from refractive index measurements[J]. International Journal of Thermophysics，1986，7(3)：709–720.

[12] KLEINRAHM R，DUSCHEK W，WAGNER W，et al. Measurement and correlation of the(pressure，density，temperature) relation of methane in the temperature range from 273.15 K to 323.15 K at pressures up to 8 MPa[J]. The Journal of Chemical Thermodynamics，1988，20(5)：621–631.

[13] PIEPERBECK N，KLEINRAHM R，WAGNER W，et al. Results of(pressure，density，temperature) measurements on methane and on nitrogen in the temperature range from 273.15 K to 323.15 K at pressures up to 12 MPa using a new apparatus for accurate gas-density measurements[J]. The Journal of Chemical Thermodynamics，1991，23(2)：175–194.

[14] 熊杰，武雅珍，韩佳昊，等. 基于模糊控制方法的加气站甲烷扩散模型选择[J]. 能源与环保，2019，41(7)：57–62.XIONG Jie，WU Yazhen，HAN Jiahao，et al. Selection of methane diffusion model in gas station based on fuzzy control method[J]. China Energy and Environmental Protection，2019，41(7)：57–62.

[15] ACHTERMANN H J，HONG Jianguo，WAGNER W，et al. Refractive index and density isotherms for methane from 273 to 373 K and at pressures up to 34 MPa[J]. Journal of Chemical & Engineering Data，1992，37(4)：414–418.

[16] SETZMANN U，WAGNER W. A new method for optimizing the structure of thermodynamic correlation equations[J]. International Journal of Thermophysics，1989，10(6)：1103–1126.

[17] WAGNER W，SPAN R. Special equations of state for methane，argon，and nitrogen for the temperature range from 270 to 350 K at pressures up to 30 MPa[J]. International Journal of Thermophysics，1993，14(4)：699–725.

[18] SETZMANN U，WAGNER W. A new equation of state and tables of thermodynamic properties for methane covering the range from the melting line to 625 K at pressures up to 100 MPa[J]. Journal of Physical & Chemical Reference Data，1991，20(6)：1061–1155.

[19] 柳辉. 解非线性方程的牛顿迭代法及其应用[J]. 重庆工学院学报(自然科学版)，2007，21(8)：95–98. LIU Hui.Newton iteration method for nonlinear equation solutions and its application[J]. Journal of Chongqing Institute of Technology(Natural Science Edition)，2007，21(8)：95–98.

[20] 杜茂康，周玉敏，等. Excel与数据处理[M]. 北京：电子工业出版社，2009.DU Maokang，ZHOU Yumin，CAO Huiying，et al. Excel and data processing[M]. Beijing：Publishing House of Electronics Industry，2009.

[21] 胡圣标，何丽娟，汪集旸. 中国大陆地区大地热流数据汇编(第三版)[J]. 地球物理学报，2001，44(5)：611–626. HU Shengbiao，HE Lijuan，WANG Jiyang. Compilation of heat flow data in the China continental area(3rdEdition)[J]. Chinese Journal of Geophysics，2001，44(5)：611–626.

[22] 王钧，黄尚瑶，黄歌山，等. 中国地温分布的基本特征[M]. 北京：地震出版社，1990. WANG Jun，HUANG Shangyao，HUANG Geshan，et al. The basic characteristics of China’s geothermal distribution[M]. Beijing：Seismological Press，1990.

[23] 张鹏，王良书，刘绍文，等. 南华北盆地群地温场研究[J]. 地球物理学进展，2007，22(2)：604–608. ZHANG Peng，WANG Liangshu，LIU Shaowen，et al.Geothermal field in the south Huabei basins[J]. Progress in Geophysics，2007，22(2)：604–608.

[24] 钟玲文. 中国煤储层压力特征[J]. 天然气工业，2003，23(5)：132–134. ZHONG Lingwen.Pressure characteristics of coal reservoirs in China[J]. Natural Gas Industry，2003，23(5)：132–134.

[25] 秦勇，申建，王宝文，等. 深部煤层气成藏效应及其耦合关系[J]. 石油学报，2012，33(1)：48–54. QIN Yong，SHEN Jian，WANG Baowen，et al. Accumulation effects and coupling relationship of deep coalbed methane[J]. Acta Petrolei Sinica，2012，33(1)：48–54.

Study on density of the supercritical methane

ZHANG Xinbin1,2, SONG Dangyu1,2, LI Yunbo1,2, QI Yong’an1,2, FAN Shunli1,2

(1. School of Resources and Environment, Henan Polytechnic University, Jiaozuo 454003, China; 2. Collaborative Innovation Center of Coalbed Methane and Shale Gas for Central Plains Economic Region, Jiaozuo 454003, China)

The density of supercritical methane is not only an important parameter for calculation of unconventional natural gas resources and adsorption capacity of methane in coal, but also a main indicator for measurement of the diffusion efficiency of supercritical methane and the ability to dissolve organic matter. Through analysis and comparison of the applicability of various gas state equations, it is realized that the Helmholtz energy state equation can accurately calculate the density of methane under the conditions of 0-30 MPa and 270-360 K. A calculation program for methane density was written using Microsoft Office Excel, and the error was less than 0.05% compared with NIST commercial software. Finally, the changing of methane density was analyzed. In the range of 0-100 MPa and 270-360 K, the density of methane increases with the increase of pressure. The increase rate is greater before 30 MPa and the sensitivity to temperature is strong. Afterwards, the growth rate gradually slows down, while the sensitivity decreases. Under the in-situ condition of the coal seam, with the increase of buried depth, the density increases with temperature and decreases with pressure. Under the combined action of temperature and pressure, the density of methane first increases approximately linearly, and the growth rate gradually decreases.The results provide basic parameters for the occurrence and potential prediction of deep CBM.

supercritical methane; methane density; gas state equation; Helmholtz energy; CBM resources

移动阅读

语音讲解

P618.11

A

1001-1986(2021)01-0137-06

2020-09-11；

2020-12-14

国家自然科学基金项目(U2003104)；河南省自然科学基金项目(202300410186)；河南理工大学青年骨干教师资助计划项目(2018XQG-04)

张新宾，1994年生，男，河南周口人，硕士，从事煤地质及非常规天然气地质学方面的研究工作. E-mail：758320669@qq.com

宋党育，1971年生，男，河北献县人，博士，教授，从事煤层气(瓦斯)地质与煤地球化学方面的研究工作. E-mail：dangyusong@hpu.edu.cn

张新宾，宋党育，李云波，等.超临界态甲烷密度研究[J]. 煤田地质与勘探，2021，49(1)：137–142. doi：10.3969/j.issn. 1001-1986.2021.01.014

ZHANG Xinbin，SONG Dangyu，LI Yunbo，et al. Study on density of the supercritical methane[J]. Coal Geology & Exploration，2021，49(1)：137–142. doi: 10.3969/j.issn.1001-1986.2021.01.014

(责任编辑 范章群)