基于时延空时滤波的P300波形提取及目标分类算法
2021-03-31林艳飞卢志强李博闻刘志文高小榕
林艳飞, 卢志强,3, 李博闻, 刘志文, 高小榕
(1.北京理工大学 信息与电子学院,北京 100081;2.清华大学 医学院,北京 100084;3.中国船舶工业系统工程研究院,北京 100094)
脑-机接口系统(brain-computer interface,BCI)[1]是一种新的人机交互方式,可以把系统采集到的脑电生理信号,通过特征提取和分类等手段进行处理后转为控制信号,从而实现与外部设备的交互.由于不依赖人的肢体动作,早期脑-机接口系统可以适用于肌萎缩侧索硬化症,脑卒中等疾病患者,提升他们的生活质量[2].目前脑-机接口系统也在应用于健康人群提高人类认知、行为和决策能力[3].脑电中包含多种成分,其中由oddball范式诱发,在刺激后 300 ms 出现的正波成分P300,是一种重要的脑电成分,是脑-机接口系统广泛使用的脑电成分.基于P300电位的脑-机接口系统有脑电打字系统[4]、脑电开关[5]、图片检索[6]、目标识别[7]等.
由于P300的信噪比很低,在传统的提取方法中,多采用大量试次叠加平均的方法提高信噪比.然而在BCI系统中,要求从少试次甚至单试次的脑电信号中提取P300成分.随着高密度脑电图记录技术的进步,出现了许多利用多通道脑电信号的空域信息实现P300少试次提取的方法,如独立成分分析(independent component analysis,ICA)[8],稀疏成分分析(sparse component analysis,SCA)[9],主成分分析(principal component analysis,PCA)[10]等.这一类方法可以在一定程度上提高脑电信号空域信息的利用率,但并不是专门针对ERP提取提出的,因而这类方法不能获得最优的性能.在过去的研究中,出现了一些专门针对ERP提取的算法,比如2006年德国FIRST Fraunhofer Institute的Lemm团队提出的正则化2阶盲分离算法(regularized second-order blind identification,r-SOBI)[11],通过提取脑电信号的锁相成分,提高信噪比,但该方法不能用于单试次的P300提取.2009年,美国佛罗里达大学的Li等[12]提出了一种基于模板的空时滤波方法,在空域进行噪声消除,从而提高信噪比.然而为了对提取出的ERP源进行约束,该方法需要预先定义ERP波形的模板,这些模板在多数情况下只能以特定方式得到,且得到方式常常是随机的,因此该方法在应用中受到一定限制.此外,为了寻求空域的最大信噪比,2011年清华大学的Wu等[13]提出了ERP信噪比最大化算法(signal-to-noise ratio maximum,SIM),该方法从多通道脑电数据中学习ERP的空时模型结构,可以实现空域的高信噪比,但没有充分利用脑电信号的时域信息.2016年,法国格勒诺布尔阿尔卑斯大学的Congedo团队提出了时域上的自适应时空共模式(adaptive common spatio-temporal pattern,aCSTP)[14],利用多变量空时滤波自动估计子空间维数,提升了信噪比,但该算法不能保证子空间维数的最优性,且无法实现源分离.2017年,清华大学的Wu等[15]提出了ERP空谱模式分析(ERP spatial and spectral patterns,ESSPs),基于循环下降的最大后验估计算法来估计空谱模式,可以很好地估计ERP,但其性能依赖于参数的选择,需要大量的训练数据进行交叉验证.
本文提出了一种基于空时滤波的P300提取及目标分类算法(时延空时滤波算法),对多通道脑电数据首先进行时延,然后以空时滤波后的信号与期望信号误差最小为目标,构造代价函数,通过交替优化的方式估计空时滤波器和源信号,最终实现空域的源分离和时域的波形提取.通过从仿真脑电数据提取P300波形和对真实脑电数据的分类,并与目前应用较为广泛的SIM作对比,验证了时延空时滤波算法的有效性.
1 算法原理
1.1 脑电信号模型
ERP信号具有相位锁定的特点,自发脑电信号通常被认为是零均值的高斯色噪声,测量噪声通常被认为是零均值的高斯白噪声[13],观测信号可以被建模为
Xk=AZ+Nk,k=1,2,…,K
(1)
式中:Xk∈RC×N为脑电观测信号,k为样本观测序号;C为信号导联数,N为信号长度;A∈RC×M为空域滤波器;M为源数量;Z∈RM×N为ERP源信号;Nk∈RC×N为自发脑电和测量噪声混合产生的噪声信号,各试次观测噪声彼此独立,方差相同[16].
1.2 算法流程图
本文提出的P300波形提取及目标分类算法流程如图1所示.首先将多通道脑电信号进行时域延时,然后构造最小二乘代价函数,循环迭代使代价函数收敛,估计得到空时滤波器和P300信号,对得到的P300信号做奇异值分解可得到空域模式和时域波形.将空时滤波器和空域模式带入训练集可以训练得到Fisher分类器,最后在测试集中进行线性判别目标分类.

图1 算法流程
1.3 算法原理
1.3.1时域延时
基于1.1节的脑电信号模型(1),对Xk的第c导联有
(2)
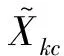
(3)
1.3.2空时滤波
时域滤波后,对式(3)中得到的结果进行空域滤波,假设存在空间滤波器B,使得
(4)
为便于分析记:W=BS,W即为最终所求的空时滤波器.后面对AZ做奇异值分解,可以得到提取的多个源信号Z和对应空域模式A,对W做分解,可以进一步求得时域滤波器和空域滤波器[17].
1.3.3交替优化
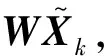
(5)
最小化式(5),即最小化:
(6)
对于式(6),有多个未知变量,无法直接求解,因此通过交替求解的方式对W和AZ分别进行优化.求解其中任一变量时,把其他变量都当作已知量处理,得到迭代公式为
首先初始化AZ,把原始样本的叠加平均作为AZ的初始值带入式(7),从而解出W,接着再把由式(7)求得的W带入式(8)更新AZ,这样便完成了一次循环迭代.通过式(5)设置阈值(如10-8),当结果满足条件时循环结束.
1.3.4P300波形提取
对AZ做奇异值分解,得到提取的多个源信号Z和对应空域模式A.根据各源成分功率大小进行排序,选取恰当的信号源和对应的空域模式.并将源成分反投至Cz电极,得到P300波形.
1.3.5P300目标分类
利用空时滤波器W和空域模式A对每个脑电信号样本提取P300源成分作为分类特征:
(9)
然后利用训练集得到的P300源成分训练Fisher线性判别分析分类器,得到分类投影矢量,将P300特征矢量变为最终的决策值,实现脑电信号的分类.
2 实验与结果
2.1 仿真实验
2.1.1数据描述
本文在P300信噪比为-20 dB,-15 dB,-10 dB,-5 dB,0 dB,5 dB的条件下生成脑电仿真数据,并提取P300波形.各信噪比下分别进行50次蒙特卡洛实验,在每次实验中,随机生成40试次的脑电信号,每个试次的信号包含30导脑电数据,每导包括250个数据点,信号采样率为250 Hz,信号由3个ERP成分和生成的背景噪声叠加得到.3个ERP成分由Gamma函数产生,在波形和出现时间上类似于典型的P100,P200和P300成分,并通过Gram-Schmidt过程正交化,如图2所示.背景噪声由20个背景自发脑电线性混叠和测量噪声组合而成.每个背景自发脑电的时间过程均为1/f噪声,测量噪声为高斯白噪声,其方差为脑电信号方差的1/6[13].ERP成分的混叠矩阵和背景脑电的混叠矩阵均为随机生成,矩阵中的所有元素都服从[0,1]均匀分布.
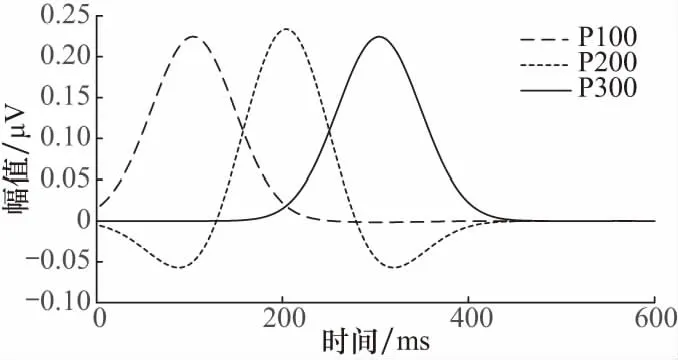
图2 3个仿真源波形
2.1.2仿真结果
在仿真实验中,已知真实波形,通过比较提取波形与真实波形的相关系数,并与近年来应用较为广泛的SIM作对比,验证本文算法的有效性.SIM基于空域滤波实现信噪比最大化,衍生了许多优秀算法,如提取失匹配负波(mismatch negativity,MMN)的重采样差分(resampling difference and SIM,rdSIM)[18],估计稳态诱发电位的ESSP等,通过与空域滤波算法SIM的比较,可以验证本算法采用空时滤波是否具有优势,因此本文仅与SIM作对比.不同信噪比下的相关系数如图3所示.可见,不同信噪比下时延空时滤波算法的相关系数要高于SIM.即便在信噪比很低(小于-10 dB)的情况下,时延空时滤波算法相关系数也大于0.7,能很好得恢复真实ERP波形,且恢复效果随信噪比的提升有明显的增强,在信噪比大于-10 dB时,相关系数已经非常接近1.
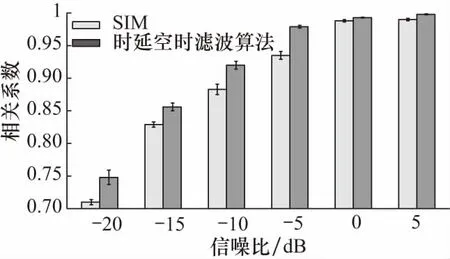
图3 两种算法在不同信噪比下的相关系数
再对时延空时滤波算法和SIM的相关系数做配对T检验,结果得出,在不同信噪比下,时延空时滤波算法的相关系数均显著高于SIM(p<0.05),说明时延空时滤波算法能更好地恢复真实ERP波形.
2.2 真实EEG数据
2.2.1实验过程及采集
数据来源为第二届BCI竞赛的数据集IIB[19],该数据由Wadsworth BCI2000软件记录[20].在实验中,给受试呈现一个6×6的字符矩阵.矩阵的每个单元格都包含一个字符,受试的任务是将注意力集中在研究人员指定单词的字符上.该矩阵的6行和6列以5.7 Hz的频率依次随机凸显.在每轮闪烁中有一个特定行和一个特定列凸显了所需的字符.与不包含所需字符刺激引起的反应不同,实验中包含所需字符的不常见刺激引起了P300反应.数据使用该数据集中一名受试者两次P300诱发电位的记录,分为11组,每组包含90个目标试次和450个非目标试次.
2.2.2结果
实验数据为64导信号,采样率240 Hz,通过0.2~28 Hz的带通滤波器进行滤波,同时进行基线校正,即减去刺激呈现前200 ms的平均电压.截取每次刺激开始后0~500 ms的数据作为样本信号,用时延空时滤波算法和SIM分别对每组数据进行P300波形提取,图4(a)~(h)分别展示了时延空时滤波算法和SIM对其中4组数据(第1、2、9、10组)的提取结果.第一行为功率较大的3个ERP源的空域模式,第二行为空域模式对应的ERP成分的时域波形,方框为挑选出来的P300空域模式及成分.第三行左图虚线为挑选出的P300源反投到Cz电极得到的P300波形,左图实线为该组所有目标试次叠加平均的波形,右图虚线为测试集中各算法处理后得到的单试次波形,右图黑实线为所有试次的均值.为了更好地展示两种算法的提取效果,分别对空域模式,时域波形和测试集中的单试次波形幅值做归一化处理.由图4第1行和第2行子图及所选源成分知,时延空时滤波算法提取的P300源在4组数据中均排在所有源的第1位,而SIM提取的P300源在第2组和第9组中排在第1位,在第1组和第10组中排在第2位;由图4第3行左子图所示,两种算法均能得到较好的反投后的P300波形;由图4第3行右子图所示,时延空时滤波算法得到的各单试次波形在4组数据中更加接近目标波形,而SIM得到的各单试次波形更接近非目标波形.
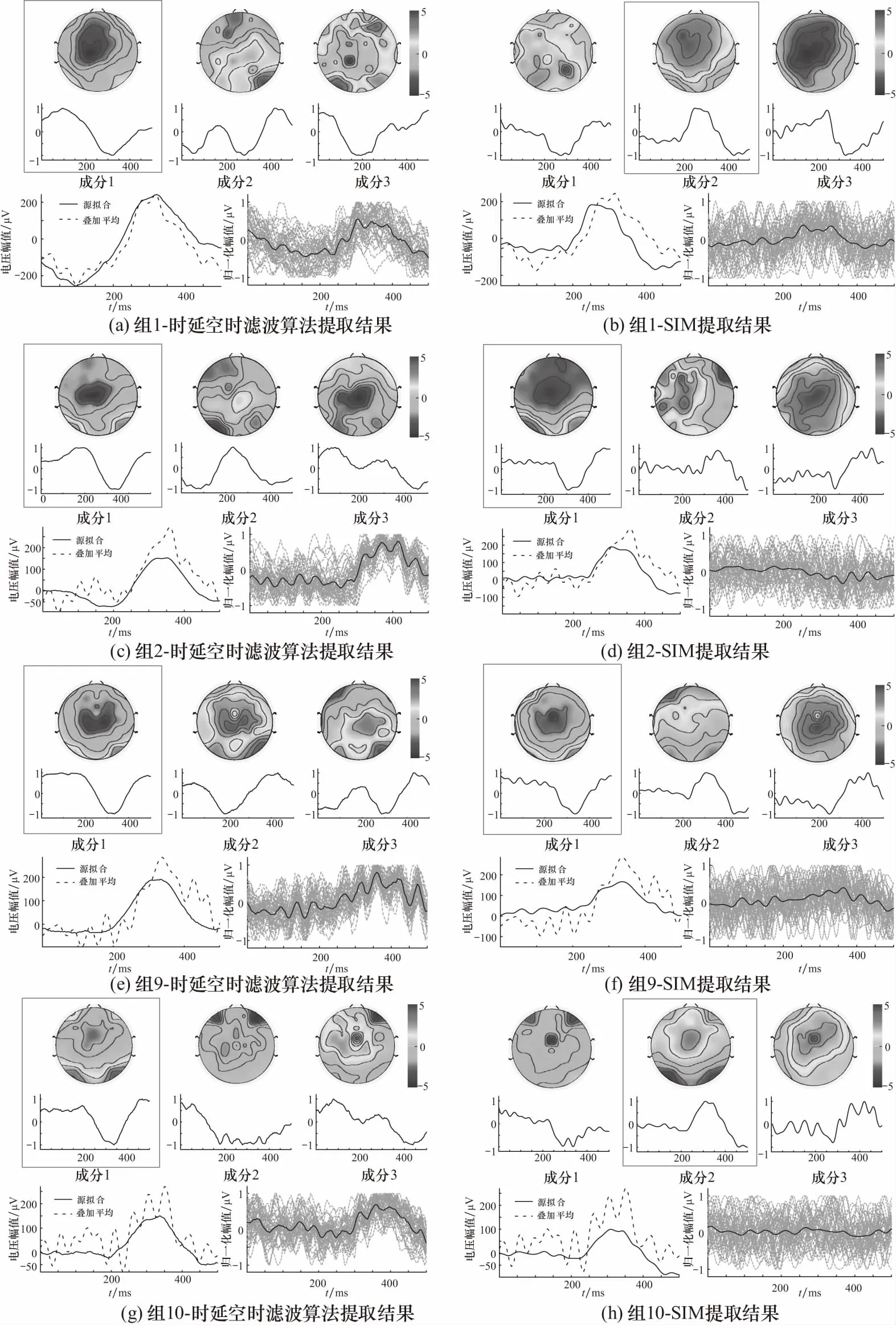
图4 两种算法P300提取效果对比
本文用所有目标试次的叠加平均波形作为参考,直观展示两种算法的提取效果.结果表明,时延空时滤波算法的提取结果在反投后的波形、相位上更加接近叠加平均的结果.而且,时延空时滤波算法得到的各单试次波形更加接近目标波形,而SIM得到的各单试次波形更接近非目标波形,因此时延空时滤波算法提取的波形更利于分类.此外,在11组数据中,时延空时滤波算法提取的P300源均排在所有源的第一位,源排序准确率为100%,具有较好的源挑选效果,而SIM的源排序准确率仅为81.8%,因此在源排序方面时延空时滤波算法要优于SIM.
为了更加准确地评价两种算法对于P300目标分类的效果,采用Fisher线性判别分析进行目标分类.将每组数据分为训练集(45目标/45非目标)和测试集(45目标/405非目标).得到如图5(a)~(d)所示的分类结果,在每个子图中,柱状图分别表示两种算法的分类准确率、AUC值、击中率和虚警率,实线表示两种算法在11组数据下的均值.

图5 两种算法的各项分类性能对比
分别对两种算法分类准确率、AUC值、击中率和虚警率做配对T检验,可以得到时延空时滤波算法的分类准确率显著高于SIM(p=0.002<0.05),时延空时滤波算法的AUC值显著高于SIM(p=0.001<0.05),时延空时滤波算法的击中率显著高于SIM(p=0.026<0.05),时延空时滤波算法的虚警率显著低于SIM(p= 0.048<0.05).因此,时延空时滤波算法的性能显著优于SIM.
3 结束语
本文提出了一种基于时延空时滤波的P300波形提取及目标分类算法.通过时域延时后约束观测信号样本与期望信号的差值,得到空时滤波的代价函数,经过交替优化使代价函数收敛后得到空时滤波器和P300信号,最后通过奇异值分解可提取P300成分的空域模式和时域波形.仿真实验和真实P300数据实验中,时延空时滤波算法均表现出良好的性能.因此,该算法可有效提取P300波形并进行目标分类.
