基于动力学模型分块逼近的水下机械臂RBF滑模控制算法研究

赵 伟， 张晓晖， 杨松楠

(西安理工大学 自动化与信息工程学院， 陕西 西安 710048)

多关节机械臂由于其灵活性，是执行水下资源勘测、水下检测维修等任务的理想工具。区别于陆用机械臂，水下机械臂在运动时会受到水作用力的影响以及多种难以预测的外部干扰[1]。分析水下机械臂的受力情况与提高水下机械臂的控制精度有助于水下机械臂的设计研发[2]。

精准的动力学模型是水下机械臂运动仿真与控制器设计的基础[3]。文献[4]通过理论分析计算了单关节水下机械臂的动力学模型。文献[5]利用Navier-Stokes方程计算了物体在水中的动力学模型，该方法求解过程复杂，不适用于多关节水下机械臂。文献[6]使用切片理论计算了水下机械臂的动力学模型，提供了新的计算思路。文献[7]使用微分变化法构建了机械臂在水环境中的动力学模型，通过仿真验证了机械臂在静水环境中受水作用力的影响，但没有计算水流对机械臂的冲击力。

实时性和抗干扰性是衡量水下机械臂控制器性能的重要指标[8]。水下机械臂是典型的多输入多输出的非线性系统，国内外研究学者针对此类系统提出了许多先进控制算法。文献[9]将前馈模糊补偿器引入滑模控制算法，用于消除动力学模型中的不确定干扰项。文献[10]使用自适应滑模控制算法实现了水下机械臂的控制，该算法具有良好的鲁棒性，但实时性仍有待提高。文献[11]和文献[12]利用径向基(RBF)网络动态逼近模型误差，提高了多关节机械臂控制器的响应速度，证明了利用前馈神经网络在多关节机械臂控制器设计中的有效性。

本文利用切片理论与Morison公式计算了双关节水下机械臂在运动时受到的水阻力、附加质量力、浮力与水流的冲击力，结合传统机械臂动力学方程推导出双关节水下机械臂在水环境中的动力学模型。基于动力学模型提出了一种RBF滑模控制策略，该策略使用多个RBF神经网络分块逼近动力学模型中的不确定项，快速补偿计算模型与实际模型的误差；使用饱和函数改进控制律，削弱控制系统的抖振效应。

1 水下机械臂动力学建模

1.1 传统机械臂动力学建模

双关节水下机械臂的结构简化示意图见图1，图中l1和l2是机械臂连杆的长度，m1和m2是连杆的质量，q1和q2代表机械臂关节的转动角度。根据图1，使用Lagrange方程求解出双关节水下机械臂的传统动力学方程如式(1)所示[13]。

图1 双关节水下机械臂结构简化示意图Fig.1 Simplified schematic diagram for double-joint manipulator

(1)

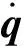
1.2 水下机械臂动力学建模

水下机械臂在水中受到的力分别为水流对静止机械臂的冲击力和机械臂在静水中运动时所受的作用力。根据流体力学，物体单位长度在静水中运动时的受到的作用力可以描述为：

(2)

式中：fd、fm、ff和fl分别为水阻力、附加质量力、浮力和升力。

本文研究的双关节水下机械臂模型的连杆均为圆柱体，因此在进行受力分析时不用考虑升力带来的影响。

Morison方程给出了水阻力和附加质量力的微分计算公式：

(3)

式中：ρ是水密度；D是连杆直径；A是连杆垂直于水流速度方向上的投影面积；v是与速度相关的函数；Cd和Cm是水阻力系数与附加质量力系数，难以直接获取精确值，一般选用经验值[14]。

根据图1中双关节水下机械臂的D-H坐标系，绘制其运动模型示意图，见图2。

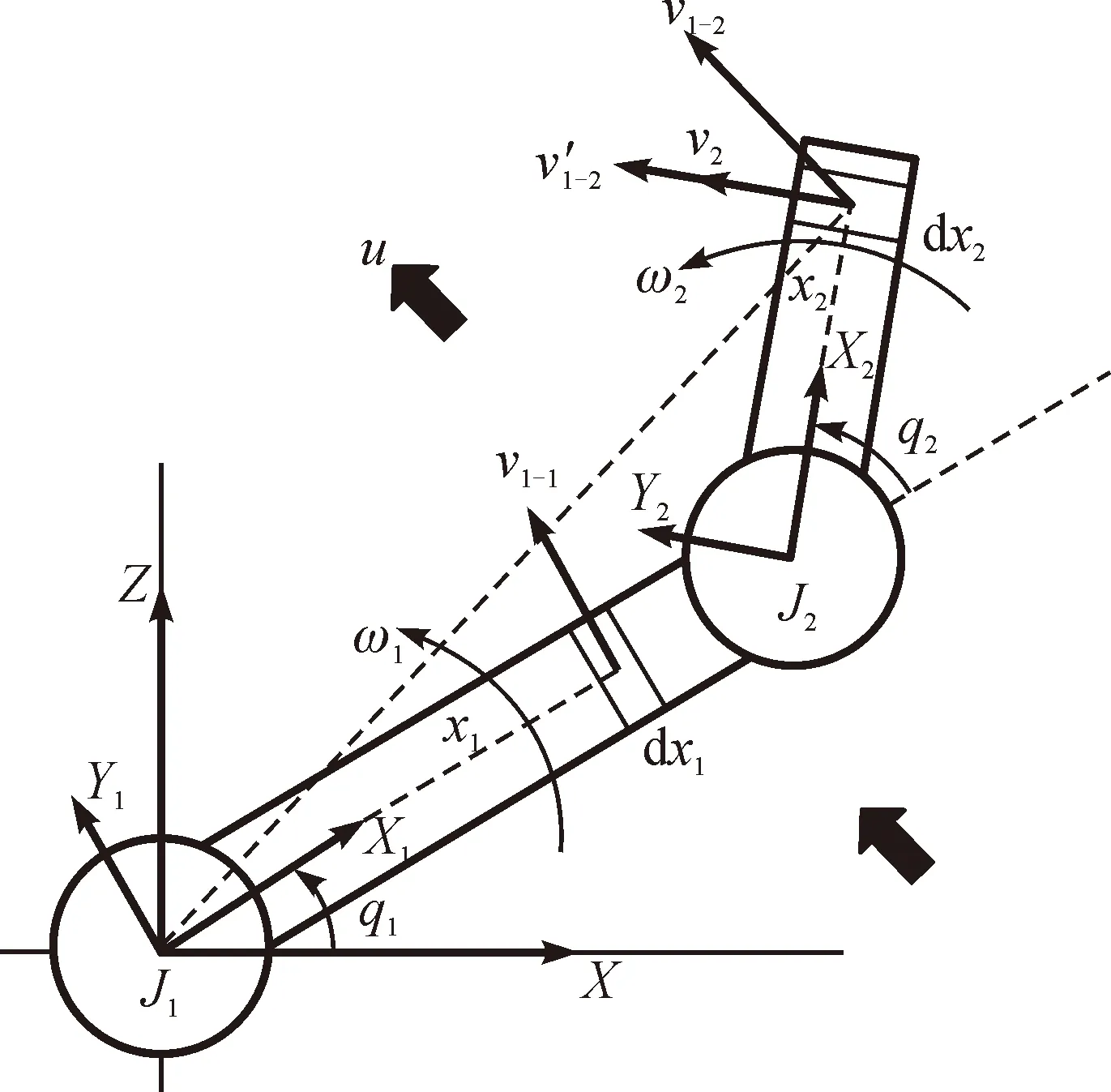
图2 双关节水下机械臂运动模型示意图Fig.2 Schematic diagram for motion model of double-joint underwater manipulator

(4)

式中：c1=cosq1，c2=cosq2。

(5)

(6)

(7)

(8)

根据式(9)和式(10)求得机械臂关节J1与关节J2受到水流冲击力矩T″1与T″2。

(9)

(10)

根据上述推导过程，可将双关节水下机械臂关节在水中受到的水作用力矩归纳为TW：

(11)

假设双关节水下机械臂各关节连杆的重心与浮心的位置重合，且重力与浮力的作用力方向相反，可根据下式求得机械臂各连杆的等效重力：

(12)

式中：mi为连杆i的质量；g为重力加速度；Vi为连杆i的体积；ρ为水密度；ρm为机械臂的等效密度。

根据式(12)与重力矩阵g求得双关节水下机械臂的等效重力矩阵g′：

g′=

(13)

式中：c12=cos(q1+q2)。

将由式(11)求得的水作用力矩阵TW与式(13)求得的等效重力矩阵g′结合式(1)可以求得水下机械臂在水环境中的动力学模型：

(14)

2 水下机械臂控制器设计

2.1 传统滑模控制

定义滑模函数为：

(15)

e(t)=qd-q

(16)

对式(15)进行求导可得：

(17)

(18)

f+εsgns+ks

(19)

式中：M′=M+Mw，C′=C+Cw。

2.2 分块逼近RBF滑模控制

将式(19)中的不确定项整理得到：

(20)

由于式(20)中包含了多个不确定参数项，使用常规RBF神经网络控制器对其进行整体逼近会产生逼近时间过长与逼近精度不足的问题。

为解决上述问题，本文使用由四个RBF神经网络组成RBF神经网络控制器对式(20)中的系数矩阵进行分块逼近，再结合滑模控制算法设计水下机械臂控制器，控制器的原理框图见图3。

图3 水下机械臂控制器设计原理框图Fig.3 Underwater manipulator controller design principle block diagram

根据上图中RBF神经网络控制器的结构可知各RBF神经网络的输入分别为：

(21)

(22)

(23)

(24)

RBF神经网络控制器的各网络隐含层均包含五个神经元，神经元内部算子均为Gauss核函数：

(25)

式中：ci为第i个神经元的中心矢量，bi为神经元的基宽度。

各RBF神经网络的自适应律分别为：

(26)

(27)

(28)

(29)

式中：FM′、FC′、Fg′与Ff均为正定矩阵。

(30)

式中：

(31)

式中：K为控制系数矩阵，A为大于0的常数。Ks+Asat(s)用于消除外部干扰τd与神经网络控制器的输出误差δ。

2.3 稳定性分析

定义正定的Lyapunov函数L：

(32)

对Lyapunov函数L进行求导可得：

(33)

(34)

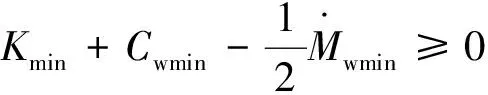
(35)

当A≥(‖δ‖+‖τd‖)时，有：

sT(τd-Asat(s)+δ)≤0

(36)

3 仿真分析

图4中展示的是在双关节水下机械臂仿真控制实验中整体逼近型RBF神经网络控制器与分块逼近型RBF神经网络控制器的输出对比。

图4 RBF神经网络控制器输出对比图Fig.4 RBF neural network output comparison diagram

从上图可以看出分块逼近RBF神经网络控制器在0.8 s附近实现了对目标值的逼近，整体逼近型RBF神经网络控制器在1.2 s附近实现对目标值的逼近。结果表明使用多个RBF神经网络对双关节水下机械臂动力学模型中的不确定参数进行分块逼近可以提高对实际模型的逼近速度，分块逼近RBF神经网络控制器相比于整体逼近RBF神经网络控制器具有更好逼近效果。

不同控制算法下双关节水下机械臂各关节的角度跟踪曲线见图5，角度的跟踪误差曲线见图6，仿真实验数据见表1。

图5 双关节水下机械臂各关节角度跟踪曲线Fig.5 Angel tracking curve of each joint of double-joint underwater manipulator

图6 双关节水下机械臂各关节角度跟踪误差曲线Fig.6 Angle tracking error curve of each joint of double-joint underwater manipulator

表1 仿真实验数据分析表

通过表1中的数据对比可知，使用RBF神经网络优化滑模控制算法可以明显提升传统滑模控制算法的性能。使用分块逼近RBF滑模控制算法时，关节1和关节2的响应时间分别为1.03 s与0.97 s，最大稳态误差分别为3.81×10-4rad与2.72×10-4rad，平均稳态误差分别为1.18×10-6rad与-3.68×10-6rad。使用整体逼近RBF滑模控制算法时，关节1和关节2的响应时间分别为1.36 s与1.32 s，最大稳态误差分别为9.67×10-4rad与6.75×10-4rad，平均稳态误差分别为4.24×10-6rad与-6.73×10-6rad。

经对比，分块逼近RBF滑模控制算法将水下机械臂的关节响应时间缩短了24%和27%，最大稳态误差减少了60%和59%，平均稳态误差减少了72%和45%。

从图7所示的关节2控制输入曲线图可以看出，当控制律中使用开关函数时，关节2的控制输入存在剧烈抖振，振动幅度为0.6 N·m。当控制律中使用饱和函数sat(s)时，关节2的控制输入的抖振现象明显减小，振动幅度为0.01 N·m。

图7 关节2控制输入曲线Fig.7 Control input curve for joint 2

仿真实验结果表明，本文提出的基于动力学模型分块逼近的水下机械臂RBF滑模控制算法相比于传统滑模控制和整体逼近RBF滑模控制可以大幅缩短水下机械臂控制系统的响应时间，降低控制系统的最大稳态误差与平均稳态误差，并能够抑制控制系统的抖振效应，实现良好的控制效果。

4 结 论

1) 通过计算双关节水下机械臂在水中运动时受到的水作用力矩，建立了双关节水下机械臂在水环境中的动力学模型。

2) 结合水下机械臂的动力学模型，提出了一种分块逼近RBF滑模控制算法，该算法缩短了对水下机械臂实际动力学模型的逼近时间，提升了逼近精度，从而缩短了控制系统的响应时间，提高了控制系统的控制精度；通过饱和函数改进了控制律，有效削弱了控制系统的抖振效应。仿真试验结果表明该算法将水下机械臂的关节响应时间缩短至1 s，稳态精度提升至3×10-6rad，满足水下机械臂的控制要求。