固定鸭舵双旋火箭弹超声速侧向气动特性

2021-03-29黄智康陈少松吕代龙

弹道学报 2021年1期

黄智康,陈少松,魏恺,吕代龙

(南京理工大学能源与动力工程学院,江苏南京 210094)

为了适应现代战争对武器精度的要求,固定鸭舵弹道修正技术凭借其控制方式简单、制导精度较高和易于集成在现有常规弹药上而得到广泛研究。固定鸭舵修正组件(precise guidance kit,PGK)是一种分离式修正组件,即修正组件的滚转速度与后体不同,因此简称双旋弹。修正组件上固定一对差动舵和一对同向舵,舵偏角是固定的,因此操纵力的大小不能随意改变,通过改变鸭舵的滚转角对弹箭进行弹道修正。差动舵在无控阶段提供导转力矩使修正组件相对后体反向旋转,同向舵在控制阶段提供控制力和力矩对弹箭进行弹道修正。

固定鸭舵弹道修正技术的大量研究工作集中在高速旋转的无尾翼炮弹上,Sahu等[1]对安装不同修正组件的炮弹的马格努斯效应进行了数值分析;吴萍[2]通过风洞试验得到双旋弹气动特性的变化规律;张蛟龙[3]建立了双旋炮弹七自由度动力学模型,结合数值仿真得到的气动系数,对无控和有控弹道特性进行分析;徐辉雯等[4]对比了双旋炮弹修正组件反旋与不旋的气动特性。

在火箭弹上安装固定鸭舵修正组件的研究集中在动力学与控制方向,在气动方面的研究比较少。王少飞[5]建立了双旋火箭弹的六自由度刚体有控弹道模型,并在此基础上分析了固定鸭舵修正组件用于火箭弹的可行性;王志刚和李伟等[6-7]用凯恩方法对双旋火箭弹进行多体动力学建模,并对其运动特性进行分析;党建涛等[8]通过数值模拟分析了双旋火箭弹在定常状态下鸭舵对尾翼的气动干扰;Yin等[9-10]对无鸭舵和有鸭舵的旋转尾翼导弹的流场进行了数值模拟,研究了有鸭舵弹箭的马格努斯效应。

鸭式布局的弹箭有着较高的控制效率,但是在安装鸭舵修正组件后,火箭弹的气动特性尤其是侧向特性会发生较大改变。首先,修正组件本身会在不旋和反旋时产生不同的侧向力;其次,由于鸭舵修正组件和后体转速不一致,鸭舵尾流会干扰弹体周围的流场,导致弹体的马格努斯效应发生改变;最后,鸭舵的下洗流会影响尾翼的气动特性,产生额外的侧向力和偏航力矩。因此,本文采用CFD软件对某双旋火箭弹的气动特性进行数值模拟,重点研究该火箭弹后体在低速旋转状态下,鸭舵修正组件不旋和反旋状态对侧向力特性的影响。

1 计算方法与研究对象

1.1 计算方法

本文使用商业流体力学计算软件ANSYS Fluent来计算弹体周围流场的三维可压缩非定常Navier-Stokes方程:

式中:V为控制体,∂V为包围控制体的封闭表面,S为控制体表面的面积,W为守恒变量矢量,Fc为对流通量矢量,Fv为黏性通量矢量。采用雷诺平均法对N-S方程进行分解。空间离散采用二阶迎风格式,对流通量应用Roe通量差分分裂。非定常计算采用双时间步法,其中物理时间描述实际运动,内迭代时间使计算收敛,二者皆采用隐式迭代求解。将定常无旋转状态的计算结果作为非定常计算的初始条件以快速稳定地得到收敛结果。

为模拟弹箭的旋转运动,本文采用滑移网格方法。如图1所示,将流场域划分为动、静2个部分,动域根据设置的方式进行平动或旋转,动、静域之间通过交界面进行数据传输。该方法相对于多重坐标系法,精度更高;而相对于动网格法,因为网格拓扑结果不需要改变而可以获得较高的网格质量。

图1 滑移网格区域划分示意图

1.2 湍流模型的选择和计算方法的验证

计算方法的验证模型为Basic Finner。远场边界为压力远场边界条件,模型边界设置为无滑移边界条件。实验数据参考文献[11],实验数据的风洞条件见表1,其中,Ma∞表示来流马赫数,p0和T0分别表示总压和总温,ReD表示基于参考长度的雷诺数,ω表示转速。

表1 实验风洞条件

在此基础上采用2种不同湍流涡黏模型,分别是S-A(Spalart-Allmaras)模型[12]和Transition SST模型[13-15],计算结果见图2,图中,Cn表示法向力系数,Cl表示滚转力矩系数。可以看到,在20°攻角以下Transition SST湍流模型计算的滚转力矩系数结果与实验值更加贴合,因此本文选择Transition SST湍流模型进行后续计算。

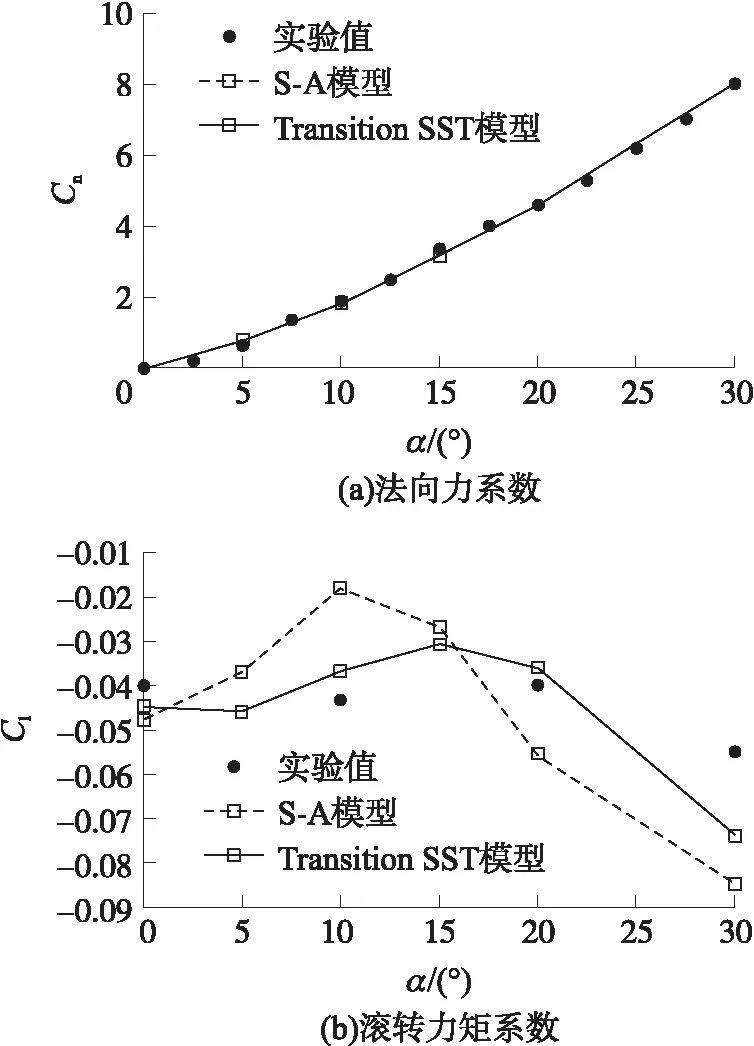
图2 气动系数计算值与实验值结果

1.3 研究对象

本文研究对象如图3、图4所示。图中,φ表示后体滚转角;φcf表示修正组件滚转角,下标cf表示修正组件。该模型弹头为固定鸭舵修正组件,弹体和尾翼组合体简称为后体。最大弹径D=106 mm,全弹长L=11.41D,其中修正组件安装一对差动舵(CANARD1和CANARD3)和一对同向舵(CANARD2和CANARD4),舵偏角δc=3°,弹尾部安装6片尾翼(FIN1,…,FIN6),尾翼斜置角δw=0.5°。参考长度为全弹长L,参考面积S=πD2/4,力矩参考点距离弹头0.45L,参考坐标系取弹体系。远场静压为101.325 kPa,静温为288.15 K。

图3 双旋火箭弹模型

图4 鸭舵和尾翼布局示意图

三维六面体网格如图5所示。计算域边界参考弹箭尺寸,轴向长度为12L,径向长度为30D。为了模拟鸭舵修正组件和后体以不同转速和方向旋转的过程,使用滑移网格方法,将计算域分为3部分。外部为静域,内部分为前后2个区域,前部包含鸭舵修正组件,后部包含弹体和尾翼。第1层网格高度设置为6×10-7m,以保证网格在壁面附近的y+<1,并使前20层网格的伸展比保持在1.1。

图5 模型网格

1.4 无关性验证

网格无关性验证的结果如表2所示,来流工况为Ma=2.0,α=6°。时间步长的无关性验证的结果如表3所示,修正组件旋转方向为X轴负向,转速为408.4 rad/s;后体旋转方向为X轴正向,转速为119.4 rad/s。表中,N表示网格数量,Δt表示时间步长,CZ表示侧向力系数,|ηCn|和|ηCZ|分别表示Cn和CZ的相对误差绝对值。

表2 网格无关性验证

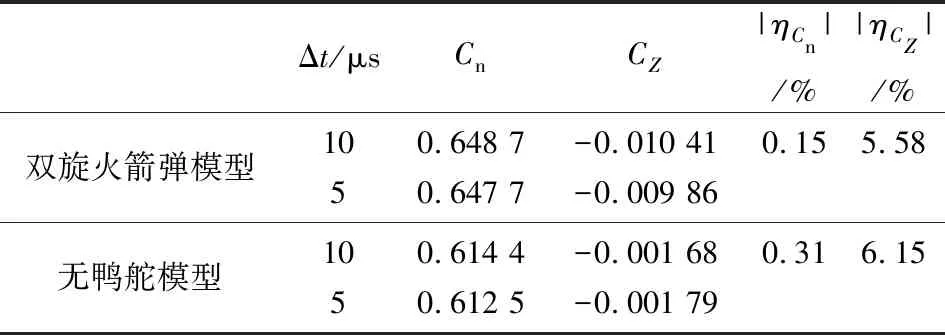
表3 时间步长无关性验证

根据计算结果,450万网格数和650万网格数的侧向力系数最大相差4.30%;时间步长为1×10-5s和5×10-6s的结果最大相差6.15%。因此,选择450万的网格及1×10-5s的时间步长,可以满足计算对网格密度和时间精度的要求。内迭代步数设置为20可满足收敛要求。

图6 双旋火箭弹气动力系数随攻角变化曲线

2 计算结果

本文给出了无鸭舵模型(NCA)、修正组件不旋(NRO)和修正组件反旋(ROT)3种状态在马赫数Ma=1.6,2.0,攻角α=0°,2°,6°,10°的平均气动力,如图6所示,图中,Ca,Cn,CZ分别为轴向力系数、法向力系数和侧向力系数。

图6中,鸭舵修正组件不旋设置为俯仰姿态修正的状态,同向舵提供正向法向力,鸭舵修正组件反旋的转速和后体转速设置为相应马赫数下α=0°对应的平衡转速(通过计算后体旋转和不旋转时的滚转力矩确定),见表4。

表4 双旋火箭弹的转速设置

加装鸭舵修正组件后轴向力系数增加,其中,Ma=1.6和Ma=2.0时修正组件在不旋状态下的轴向力系数相对于无鸭舵模型分别增加了约1.3%和1.5%,反旋状态下的轴向力系数相对于无鸭舵模型分别增加了约0.7%和0.9%。

法向力系数随攻角和马赫数的增大而增大。图7给出了修正组件反旋时修正组件法向力系数随滚转角周期性变化曲线。图7及后文图中,下标b表示弹体,f表示尾翼,aft表示后体,cf表示修正组件。由图7可知,修正组件反旋时的法向力较不旋时提供的平均法向力小,但由于修正组件提供的法向力始终为正,因此反旋状态的平均法向力比无鸭舵模型大。

图7 Ma=1.6,α=2°,6°时鸭舵修正组件反旋时修正组件法向力系数随滚转角φcf变化曲线

在加装鸭舵修正组件后侧向力系数随攻角非线性增加,修正组件反旋的状态下其侧向力系数增加量有所减少,即反旋的状态有助于抑制侧向力随攻角的增加。

图8给出了Ma=1.6时修正组件弹体和尾翼的部件侧向力随攻角变化曲线。无鸭舵模型的弹体和尾翼提供的侧向力大小大致相同,方向相反。安装鸭舵修正组件后,弹体和尾翼的侧向力显著增加,其中弹体提供的侧向力比尾翼大很多。小攻角时,修正组件反旋的弹体和尾翼侧向力随攻角变化的增量小于不旋状态;随着攻角的进一步增加,反旋状态的弹体和尾翼侧向力逐渐超过不旋状态。同时α=10°时,修正组件不旋时尾翼的侧向力并不会随着攻角增加而持续增加,而是保持与无鸭舵模型相近的大小。

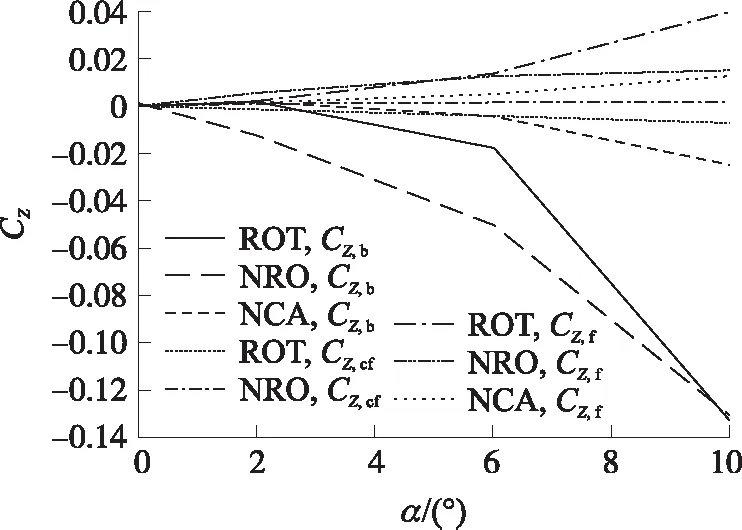
图8 Ma=1.6时部件侧向力系数随攻角变化曲线

弹头的鸭舵修正组件本身提供的侧向力在不旋和反旋时方向相反,相对于尾翼和弹体而言是一小量,但是由于其离质心距离较远,所以仍会提供不容忽视的偏航力矩。鸭舵修正组件和后体偏航力矩曲线见图9。由图可见,反旋状态下修正组件提供的偏航力矩最高能达到全弹偏航力矩的40%。

2.1 无鸭舵模型侧向气动特性分析

对于无鸭舵模型,小攻角时无论是弹体还是尾翼的侧向力都很小,仅在α=10°时侧向力才有明显的增加。图10为无鸭舵模型在Ma=1.6,α=10°时,弹体段4个截面上的无量纲涡量Ω*(Ω*=ΩD/v∞,其中Ω表示涡量大小,v∞表示来流速度)云图和空间流线图。如图所示,弹体前段x/L=0.22处并未发生流动分离。在弹体的中后段,来流绕过弹体形成分离涡附着在弹体上表面,并且体涡区随着轴向距离增加而扩大。尽管弹体低速旋转会使弹体涡随轴向距离增加,略微沿旋转方向偏转,但是整体流场仍保持左右对称,产生的侧向力系数也相应较小。

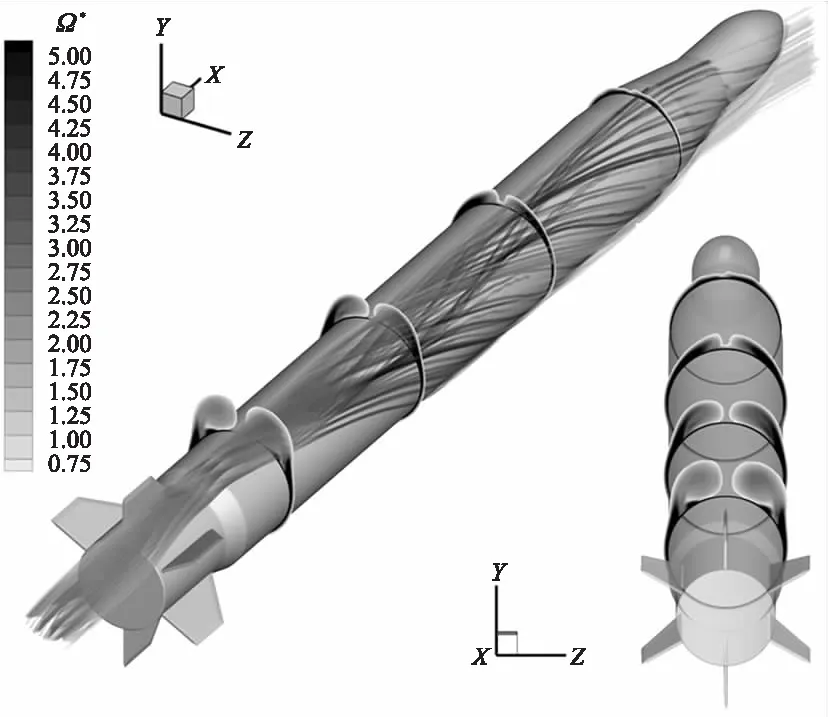
图10 Ma=1.6,α=10°,无鸭舵模型x/L=0.22,0.42,0.62,0.82处无量纲涡量云图和空间流线图

图11为无鸭舵模型弹体4个截面处的压力系数Cp沿周向分布曲线。弹体旋转产生马格努斯力的主要原因在于φ=90°和φ=270°附近的压力系数。在x/L=0.22处,弹体绕流并未分离,压力系数曲线分布左右对称。随着边界层沿轴向发展,流动发生分离,导致左右两侧的压力系数不对称加剧。同时弹体分离涡处的压力系数分布也受旋转影响,产生的正向侧向力与上面所描述的侧向力方向正好相反,但由于这部分影响作用在弹体上表面,因此产生的侧向力并不大。

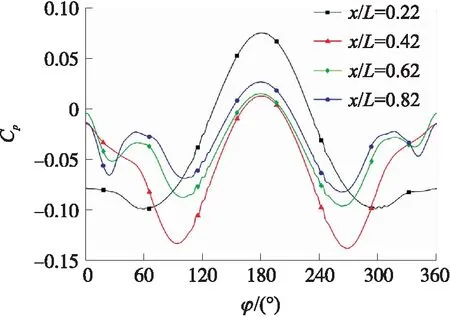
图11 Ma=1.6,α=10°,无鸭舵模型不同x/L处的压力系数沿周向分布曲线

图12是无鸭舵模型尾翼FIN1旋转一周提供的侧向力。小攻角时,弹体上表面涡迹较小甚至没有,对尾翼影响也只限于翼根,此时尾翼产生的侧向力很小。如图12中α=2°的曲线,在平衡转速下侧向力曲线呈现振幅相等的2个振荡周期。随着攻角增加,弹体涡影响范围扩大,对尾翼的侧向力产生影响。如图12中α=10°的曲线,在背风区(φ∈[0°,90°]∪[270°,360°]),侧向力曲线左右出现不对称,同时在φ=0°附近产生了第3个振荡。图13给出了α=10°时尾翼在φ=0°附近的流线图,由图可见,弹体两侧的绕流在顶部汇聚,在φ=0°附近,当地流动方向会发生偏折,改变了尾翼侧向力的方向,由此产生了第3个振荡周期。

图12 Ma=1.6,无鸭舵模型FIN1提供的侧向力系数随滚转角φ变化曲线

图13 Ma=1.6,α=10°,无鸭舵模型表面压力系数云图和空间流线图

2.2 修正组件不旋时侧向气动特性分析

当鸭舵修正组件不旋时,其本身产生的侧向力来自攻角的影响。当同向舵处于横向平面而提供额外升力时,差动舵处于纵向平面并提供一个负的滚转力矩,如果此时攻角不为0,那么此时处于迎风面的差动舵提供的正向侧向力将大于背风面差动舵提供的负向侧向力。图14为迎风侧和背风侧鸭舵表面压力系数云图,可以清晰地观察到迎风面鸭舵上下表面压差大于背风面鸭舵上下表面的压差。

图14 Ma=1.6,α=6°,鸭舵修正组件不旋时背风侧鸭舵(CANARD1)和迎风侧鸭舵(CANARD3)表面压力系数云图

图15给出了无鸭舵模型和修正组件不旋状态下弹体截面侧向力系数轴向分布曲线。加装鸭舵修正组件后,侧向力系数增加明显。从x/L=0.26至x/L=0.88,截面侧向力系数负向增加,且攻角越大,其变化的斜率越大。在x/L=0.26之前和x/L=0.88之后,因截面不连续变化,弹体截面侧向力出现震荡变化。并且弹体尾部区域受到尾翼干扰,截面侧向力随轴向距离增加迅速减小,方向变为Z轴正向。由此可见,弹体提供的侧向力主要集中在弹体中后段。

图15 Ma=1.6,无鸭舵模型和修正组件不旋时弹体截面侧向力系数沿轴向分布曲线

鸭舵的尾涡和弹体的相互干扰是弹体侧向力增加的主要原因。为了进一步分析鸭舵尾涡对弹体周围压力分布的影响,给出弹体不同截面的压力系数周向分布曲线和涡量云图,如图16和图17所示。

由图可见,在小攻角时,鸭舵尾涡分布在弹体φ=0°,90°,180°,270° 4个方向上。在尾涡对应的位置,弹体的压力系数会出现波动,波动的幅度与当地尾涡的强度有关。显然,轴向距离越小,鸭舵尾涡更强,波动幅度就会更大;同向舵的当地攻角是舵偏角和来流攻角之和,其尾涡强度比处于俯仰平面的差动舵更强,因此,φ=90°和φ=180°方向的波动幅度更大。从压力系数曲线和涡量云图中可以观察到,压力系数发生波动的位置随着轴向距离的增加而改变,攻角不为0,使得尾涡呈现向上偏移的趋势;弹体旋转使得尾涡随着轴向距离增加略微向着旋转方向偏移。

图16 Ma=1.6,无鸭舵模型和修正组件不旋时x/L=0.22,0.42,0.62,0.82处压力系数周向分布曲线

图17 Ma=1.6,修正组件不旋时弹体截面的无量纲涡量云图和流线图

α=10°时,受迎风面的影响,180°方向的尾涡很快就消失了,因此弹体底部的压力系数与无鸭舵模型完全一致。φ=0°方向的尾涡因为向上偏移,对弹体表面的影响变小。φ=90°和φ=270°方向的鸭舵尾涡在随着轴向距离增加并上移的过程中,不仅会直接影响弹体表面的流动,而且和弹体体涡相互干扰,且旋转使涡流顺时针偏移,从而使得涡流在弹体背风面呈现非对称的分布,在压力系数曲线图上表现为左右不对称的加剧;同时,在弹体顶部区域,无鸭舵模型弹体背风面存在的正向侧向力也因受鸭舵尾涡的影响而大幅减弱。

为了确定鸭舵对尾翼的影响,图18给出了在鸭舵组件不旋状态下单独FIN1旋转一周的侧向力,并与无鸭舵模型对比。对比结果表明,鸭舵尾流对迎风面尾翼基本没有影响,主要影响区域集中在背风区;且随着攻角增大,影响区域逐渐减小。这种影响主要来自于鸭舵尾涡和弹体体涡的互相干扰,使得尾翼段流场更加复杂并且失去对称性。当α<6°时,影响区域有侧向力正向增加的现象,而在α=10°时尾翼的侧向力并没有明显增加的趋势。

图18 Ma=1.6,无鸭舵模型和修正组件不旋时FIN1提供的侧向力系数随滚转角φ的变化曲线

图19给出了不同攻角时鸭舵尾流流线图和尾翼处截面的压力云图。由图可见,随着攻角增加,鸭舵尾流对尾翼的影响区域逐渐变小,同时弹体两侧的鸭舵受来流攻角的影响最大,因此尾涡更强。迎风面鸭舵的尾流对尾翼影响不大,因此图中没有给出。当α=2°和α=6°时,背风侧和弹体两侧鸭舵尾流能够直接影响尾翼区域,因此处于φ=0°附近的尾翼上下表面压力系数分布改变非常明显。当α=10°时,弹身两侧的鸭舵尾涡更强,对背风面的压力系数改变更加明显,但是其对尾翼段流场的直接影响区域超过了尾翼的展长,因此并没有加剧尾翼侧向力,这与图8和图18中尾翼侧向力并没有随攻角进一步增加的结果相符。

图19 Ma=1.6,无鸭舵模型和修正组件不旋时鸭舵尾流流线图和x/L=0.97处截面压力云图

2.3 修正组件反旋时侧向气动特性分析

鸭舵修正组件在反旋时提供的侧向力会比不旋状态大,同时方向相反,因为此时鸭舵不仅产生侧向力,也会干扰弹头旋转体反旋的马格努斯效应,二者随修正组件滚转角φcf变化的曲线见图20,图中,CANARDs表示4片鸭舵之和。

图20 Ma=1.6,修正组件反旋时鸭舵侧向力系数随修正组件滚转角φcf变化曲线

单片鸭舵提供的侧向力的幅值随攻角增加而增加,但4片鸭舵的总侧向力却并没有增加很多。总侧向力曲线的极值对应φcf=90°和φcf=270°,此时同向舵正处于纵向平面内,产生最大的瞬时侧向力。

3片舵偏角与滚转方向相同的鸭舵(CANARD1,CANARD2,CANARD3),其侧向力曲线幅值相同,随滚转角变化只相差90°的相位,而另外的1片鸭舵(CANARD4),由于其舵偏角方向与滚转方向相反,因而侧向力曲线的幅值更大。这就导致当攻角不为0时,CANARD4于迎风面和背风面产生的侧向力的差值也要比其余鸭舵大得多。修正组件反旋时,鸭舵会干扰弹头旋转体段的马格努斯力,如图20所示,最主要的变化集中在φcf=270°附近,且随着攻角增大,该影响也随之增大,结果使侧向力增加。

图21给出了修正组件反旋时弹体截面侧向力系数沿轴向分布。由图可见,修正组件反旋相比不旋情况,弹体前半段侧向力增加较小。同时,当α=2°和α=6°时,反旋时弹体的侧向力增量相比不旋状态也小很多,仅在α=10°时,侧向力系数随轴向距离增加而大幅增加。

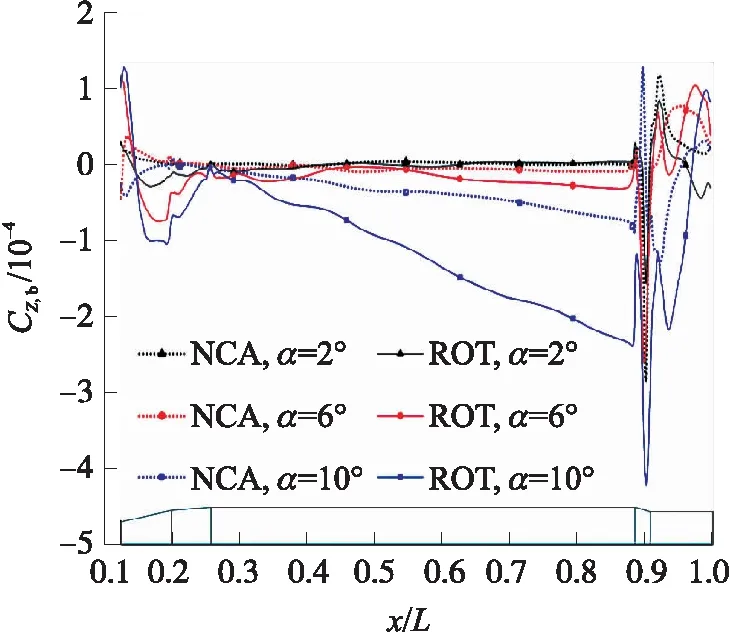
图21 Ma=1.6,无鸭舵模型和修正组件反旋时弹体截面侧向力系数沿轴向分布曲线

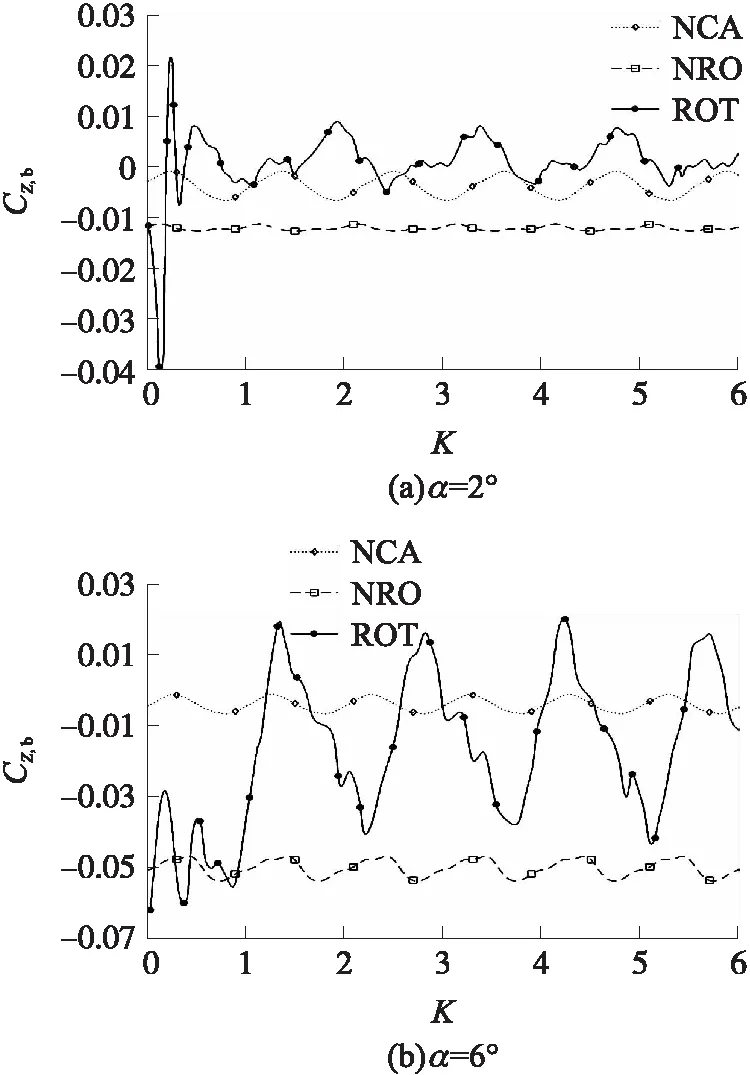
图22 Ma=1.6,弹体瞬时侧向力系数随时间变化曲线

图23对比了FIN1在组件不旋和反旋状态下旋转一周的侧向力系数。当α<6°时,侧向力系数与修正组件不旋时大致相同,反旋时鸭舵对尾翼的主要影响同样集中在背风区。主要的区别在于,α=10°时,尾翼侧向力系数有明显增加,这也与图8中所述一致。原因在于,修正组件反旋后,鸭舵的尾流在背风区周期变化,不仅对尾翼段的影响范围变大,而且此时鸭舵尾流会直接影响尾翼,导致尾翼侧向力增加。