强冲击载荷作用下Halbach阵列电涡流阻尼器动力学特性仿真分析

李启坤,葛建立,李加浩,杨国来,孙全兆

(南京理工大学 机械工程学院,江苏 南京 210094)

电涡流阻尼器是一种基于涡流阻尼原理的缓冲装置。根据电磁感应定理可知,当导电体和磁场发生相对运动时,会在导电体中感应出涡流,并且该涡流会激发感应磁场。又由楞次定律可知,该感应磁场的作用是阻碍导电体与磁场的相对运动,即对导电体施加一个阻尼力[1]。电涡流阻尼器具有结构简单、初级与次级之间没有接触和制动力可控等优点,是一种非接触阻尼方式。其在高铁制动、空间对接和桥梁高楼减震等领域应用十分广泛[2]。

火炮发射时,火药气体产生作用时间极短、峰值极大的炮膛合力,这对火炮的反后坐装置设计提出了极高的要求。制退机作为火炮反后坐装置的关键部件之一,可在火炮发射的过程中产生一定的阻力用于消耗后坐能量,将后坐运动限制在规定的长度内[3]。传统的液压式火炮制退机在长期使用中会存在制退液失效和泄漏等问题,导致制退机性能和可靠性严重下降,且后期维护比较复杂,容易造成环境污染[4-5]。因此,将电涡流阻尼器应用在火炮反后坐高速制动领域具有重大前景。目前,已有学者将电涡流阻尼器应用在火炮反后坐装置中。例如,黄通等[6]提出了一种可通过控制负载阻值进而调控制退阻力的新型电涡流制退机结构设计方案;李子轩等[7]设计了一种永磁式圆筒型电涡流制退机,并对电涡流制退机进行了强冲击载荷作用下的阻尼特性研究和后坐阻力突变优化研究。现有结构大多采用了传统的轴向或径向充磁方式的永磁阵列,激励的磁场分布具有对称性,永磁体利用率低,容易漏磁,且装置质量相较于传统制退机大大增加,不利于火炮的机动性。而Halbach永磁阵列具有以下优点[8]:阵列磁场呈现出一边“强”磁场,一边“弱”磁场的特点,不易漏磁,所以不需要添加屏蔽装置;产生的单边磁场性不需要软磁材料为其提供磁路,大大降低了自身质量。因此,强冲击载荷下Halbach阵列电涡流阻尼器的阻尼特性具有重要研究价值。

本文以某中大口径火炮为研究对象,通过考虑永磁体的利用率,使用Halbach永磁阵列,提出了一种基于Halbach阵列的电涡流阻尼器结构设计方案,介绍了其基本结构和工作原理。利用Comsol软件建立电涡流阻尼器的有限元仿真模型,引入火炮后坐运动方程,通过确定激励源和添加边界条件,计算出电涡流阻尼器的涡流阻尼力,火炮后坐阻力、后坐速度和后坐位移。最后,分析了电涡流阻尼器尺寸参数和同轴偏心误差对阻尼特性的影响。

1 Halbach阵列

Halbach阵列是一种新型永磁排列方式,且完全由稀土永磁材料构成,通过将不同充磁方向的永磁体按照一定规律排列而成[9]。

由于理想的Halbach阵列加工装配工艺复杂,一般工业上采用磁块拼接成的非理想的Halbach阵列。本文使用的Halbach直线型永磁阵列是由径向充磁和轴向充磁按一定规律排列的,图1为其二维充磁示意图,显示了磁力线的合成效果。

图1 直线型Halbach磁场线合成图

利用Comsol软件二维磁场稳态计算模块对图1所示的Halbach阵列进行仿真,永磁体选择高性能的稀土永磁材料钕铁硼N38,仿真结果如图2、图3所示。由图可知,Halbach阵列一侧磁场线分布较密集,一侧较稀疏,且强磁场一侧沿y方向的磁场强度呈正弦分布。因此可采用Halbach阵列,以提高永磁体的利用率,减轻电涡流阻尼器的质量。

图2 Halbach阵列磁通密度云图

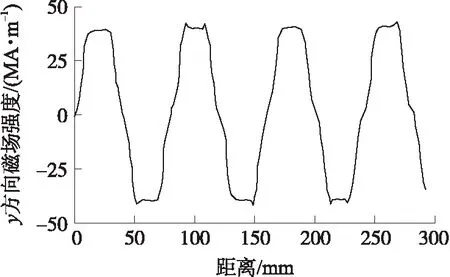
图3 Halbach阵列y方向磁场强度曲线

2 基本结构

永磁式电涡流阻尼器不需要外部电源,特别是使用直线型Halbach阵列,制动密度较高,维护简单,便于控制,但无法控制其励磁效果[10]。本文根据火炮后坐运动特性和整体结构,选择圆筒型永磁式电涡流阻尼器设计方案,其结构简图如图4所示。

该电涡流阻尼器主要由初级结构和次级结构组成。初级结构包括身管、隔热层、永磁体、轭铁,次级结构包括内筒和摇架长圆筒。内筒与摇架长圆筒为固定连接关系;隔热层、身管和永磁体为固定连接关系。隔热层的主要作用是减小身管传热对永磁体磁通性能的削弱,轭铁的主要作用是减小Halbach阵列端部漏磁。内筒和永磁体之间存在空气间隙,使得永磁体、气隙和内筒之间构成一个闭合的磁路。当初级与次级发生相对运动时,内筒上会形成类似涡旋的电流。根据楞次定律,该涡流会激发与原磁场方向相反的感应磁场,并与原磁场相互作用产生涡流阻尼力,该力总是阻碍初级与次级的相对运动。

图4 电涡流阻尼器结构简图

3 电涡流阻尼器动力学特性分析

3.1 动力学仿真数学模型

图5为直线型Halbach阵列电涡流阻尼器阻尼力分析模型,图中箭头方向代表磁块充磁方向。

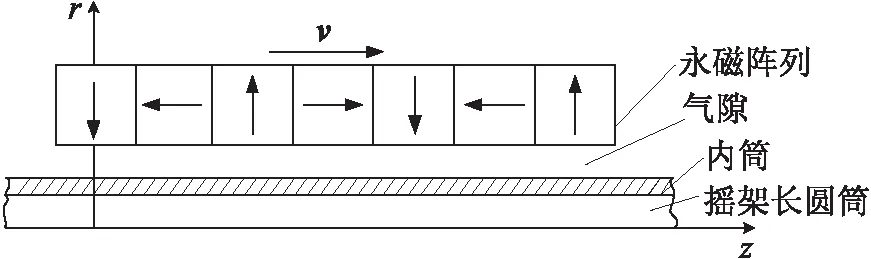
图5 涡流阻尼力分析模型

当初级与次级的相对运动速度为v(后坐运动速度)时,内筒上的电流密度为

J=σ(v×B)

(1)

式中:σ为内筒的电导率,B为内筒感应出的磁感应强度,v为后坐运动速度。

基于洛伦兹力公式可得涡流阻尼力:

(2)

式中:V为内筒体积,Br为内筒径向磁场强度,且涡流阻尼力仅与内筒径向方向磁场强度有关。

引入火炮后坐运动方程:

(3)

式中:mh为后坐质量,v为后坐运动速度,Fp为炮膛合力,Ff为复进机力,FT为摇架导轨的摩擦力,φ为火炮高低射角。

令后坐阻力为FR,则

FR=Fe+Ff+FT-mhgsinφ

(4)

由于Halbach阵列永磁阵列激励的内筒磁感应强度大小数学推导计算复杂,具体可参考文献[11],为计算方便,在简化模型和合理假设的前提下,大多数学者采用有限元分析法进行涡流阻尼特性分析。

3.2 电涡流阻尼器有限元仿真分析

在对电涡流阻尼器进行瞬态有限元仿真时做如下假设:①忽略内筒涡流损耗产生的热量对永磁体性能的影响;②忽略电涡流阻尼器内部的漏磁;③忽略初级和次级在运动过程中产生的弹性变形。选用多物理场耦合软件Comsol的磁场模块研究本文的电涡流阻尼器的阻尼特性,同时Comsol软件也能够求解火炮后坐运动的偏微分方程。由于其结构是由多个旋转体构成,为保证计算速度和计算精度,选用二维轴对称空间维度进行分析计算。

图6为电涡流阻尼器的二维建模局部示意图。在建立仿真模型时需要对模型进行简化,由于不考虑温度和Halbach阵列端部磁场对阻尼特性的影响,建模时忽略对磁场影响较小的隔热层和轭铁。永磁体与内筒之间存在空气间隙,形成气隙磁场,二者通过相对运动产生涡流阻尼力,完成力和能量的相互转换。为模拟初级和次级的相对运动,后坐运动部分采用动网格数学模型。模型运动经过的区域采用映射矩形网格,其余部分采用自由三角形网格进行网格划分,仿真模型各部分的仿真参数如表1所示。

图6 电涡流阻尼器动力学建模局部示意图

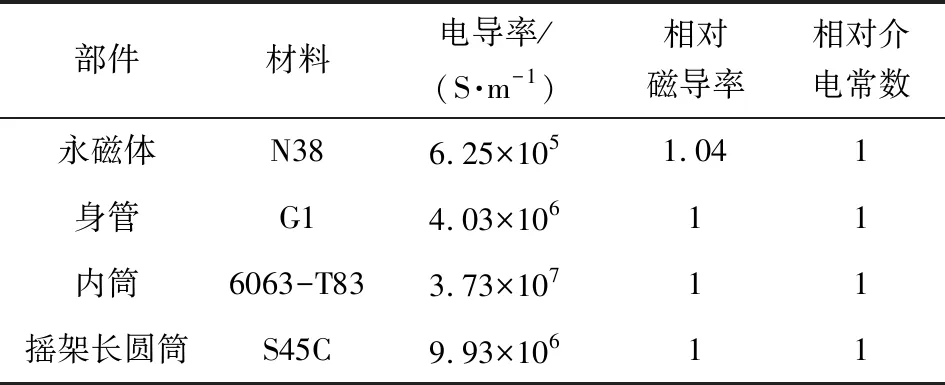
表1 电涡流阻尼器各部件仿真参数

编写火炮炮膛合力载荷激励函数,得到任意时刻的炮膛合力曲线,如图7所示。由于复进机力是由弹性介质提供的,根据火炮的复进要求选定复进机弹性介质和结构参数后,后坐过程中复进机力是后坐行程的函数[5],如图8所示。忽略密封装置摩擦力和摇架与导轨之间的摩擦力,将炮膛合力和复进机力曲线导入有限元计算模型中,计算得到涡流阻尼力以及后坐运动过程中的后坐阻力、后坐速度和后坐位移。

图7 炮膛合力曲线

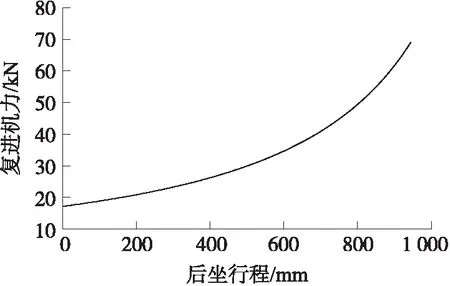
图8 复进机力曲线

图9为气隙磁通密度模最大值在0～13 ms期间的变化曲线,由图可知,6～10 ms时期气隙磁通密度模最大值呈现下降趋势,说明内筒感应出的磁场与Halbach永磁阵列激励的原磁场作用后,发生“退磁”现象,即炮膛合力作用时期,气隙存在“退磁”现象。

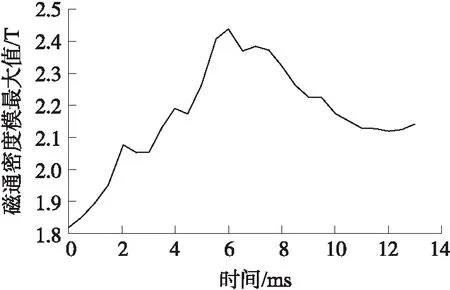
图9 气隙磁通密度模最大值变化曲线

图10为电涡流阻尼器与传统制退机后坐速度变化规律曲线。与传统制退机后坐速度计算结果及文献[7]对比表明,后坐速度符合火炮后坐运动规律,电涡流阻尼器在火炮后坐运动过程中可以提供满足后坐运动要求的阻尼力。图11为后坐位移变化规律曲线,由图可知,后坐位移增值呈现出先迅速增大后又逐渐放缓的趋势。同时后坐速度迅速增大到峰值后又逐渐减小,说明基于电涡流阻尼器的火炮后坐运动特性符合火炮后坐运动规律。

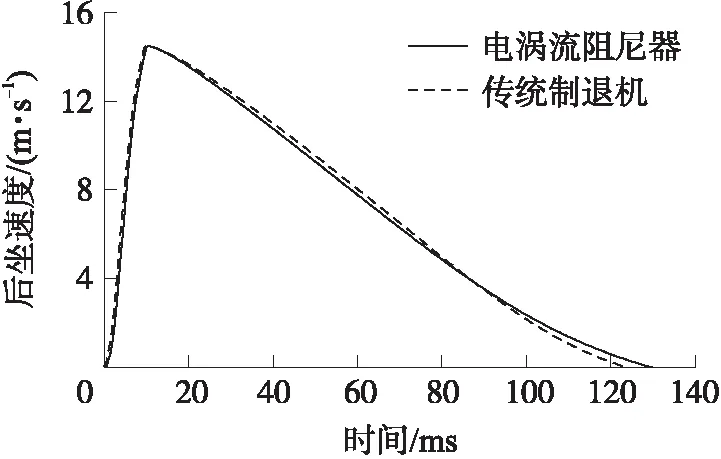
图10 后坐过程速度曲线

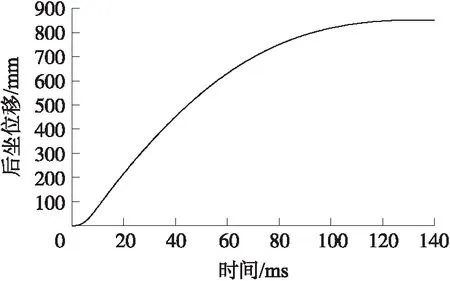
图11 后坐过程位移曲线

图12为后坐阻力变化规律曲线。由图可见,在0～6.5 ms炮膛合力作用时期,由于“退磁”效应的存在,后坐阻力增大至某一峰值,此时后坐速度也达到峰值,随后后坐阻力又迅速下降至某一谷值。之后的复进机力作用时期,后坐速度下降较快,后坐阻力下降后又达到一个峰值,曲线形成“马鞍”形状。通过与前面学者所做的火炮后坐运动研究进行比较,仿真结果表明电涡流阻尼器的阻尼特性可以满足火炮的后坐运动特性。

图12 后坐阻力曲线

3.3 电涡流阻尼器关键尺寸参数影响分析

电涡流阻尼器产生的涡流阻尼力大小与永磁阵列产生的磁场分布密切相关,而影响磁场分布的尺寸参数有气隙宽度b、内筒厚度δ1和永磁体厚度δ2。

①气隙宽度。由于空气的磁阻远远大于内筒,所以改变气隙宽度会造成涡流阻尼力很大的变化。图13为不同气隙宽度的涡流阻尼力变化规律。气隙宽度从0.5 mm增大至5 mm时,涡流阻尼力的峰值也逐渐减小,电涡流阻尼器的工作时间也逐渐增大。这说明随着气隙宽度的增大,空气的磁阻增大,内筒感应出的涡流将逐渐减小,涡流阻尼力中间时刻的曲线平台高度也逐渐下降。

图13 涡流阻尼力随气隙宽度变化规律

②内筒厚度。当永磁体厚度确定后,可通过调整内筒厚度确定气隙的宽度。图14为不同内筒厚度的涡流阻尼力变化规律。由图可知,内筒厚度在2～6 mm时,由于内筒上感应出的涡流面积增大,涡流感应的磁场会相应增大,导致内筒上的磁通密度减小,产生的涡流密度减小,电涡流阻尼器的工作时间逐渐增大,同时涡流阻尼力的峰值逐渐减小。此外,涡流感应出的磁场也会造成气隙的磁感应强度减小,涡流阻尼力曲线的平台效应不断削弱。

图14 涡流阻尼力随内筒厚度变化规律

③永磁体厚度。当永磁体的材料确定后,永磁体主要性能包括充磁方向上的厚度和磁势[12]。图15为不同永磁体厚度的涡流阻尼力变化规律。由图可知,永磁体厚度从16 mm增大至24 mm时,电涡流阻尼器的工作时间逐渐减小,而涡流阻尼力的峰值逐渐增大,所以可通过增加永磁体的厚度来增大磁场强度,但永磁体的质量也随之增大。

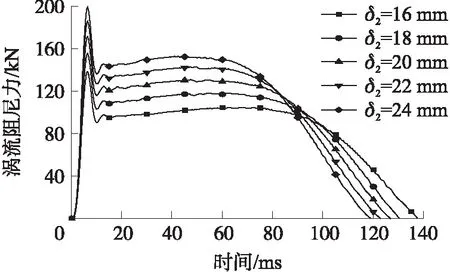
图15 涡流阻尼力随永磁体厚度变化规律

从图13～图15可知,改变气隙宽度、内筒厚度和永磁体厚度,涡流阻尼力均会出现“马鞍”曲线形状,这在火炮工程实践上是非理想化的现象,也是本文设计的电涡流阻尼器的不足之处。出现这种现象的主要原因是,随着后坐速度的增大,涡流感应出的磁场强度增大,“退磁”效应逐渐显著,使内筒上的磁通密度减小,涡流阻尼力下降较快。

3.4 电涡流阻尼器同轴偏心误差影响分析

由图13可知,涡流阻尼力的大小与气隙宽度有着密切的关系。由于电涡流阻尼器各部件的加工工艺和装配误差,内筒与永磁体很难处于同轴位置,导致气隙宽度存在偏心误差,如图16所示。

图16 偏心误差示意图

假定内筒和永磁体同轴时的1.5 mm气隙宽度的理想工况为正常工况,通过改变气隙位置和形状,分别仿真计算偏心距离a为0.5 mm,0.8 mm,1 mm时的偏心工况,其余仿真参数保持不变。其仿真结果对比如图17所示。

图17 偏心工况涡流阻尼力曲线

由图可知,正常工况和偏心工况仿真计算所得的涡流阻尼力大小变化规律相同,且电涡流阻尼器工作时间几乎一样,偏心工况复进机作用时期的峰值均增大。定义涡流阻尼力峰值误差计算公式:

(5)

式中:F为正常工况下的涡流阻尼力峰值,F′为偏心工况下涡流阻尼力峰值。

计算所得0.5 mm,0.8 mm,1 mm的偏心工况下的涡流阻尼力峰值误差分别为2.11%,4.23%,5.61%。计算可知,当偏心误差增大时,涡流阻尼力峰值误差随之增大,但误差数值较小,通过减小加工装配偏心误差可以减小涡流阻尼力峰值误差。

4 结束语

本文设计了一种Halbach阵列电涡流阻尼器,通过仿真分析了火炮后坐运动下的电涡流阻尼器的动力学特性。仿真结果表明:①Halbach阵列的永磁体利用率高,且在强冲击载荷作用下电涡流阻尼器的阻尼特性能够满足火炮后坐运动特性要求;②改变电涡流阻尼器的尺寸参数值可以得到不同的涡流阻尼力曲线,且由于“退磁”效应的存在,涡流阻尼力曲线都会出现“马鞍”形状,后面可通过对涡流阻尼力进行优化研究,消除“马鞍”曲线形状;③电涡流阻尼器同轴偏心误差的存在会影响涡流阻尼力的峰值。