巧用坐标轴绘制三视图和轴测图

宫丽华

（承德应用技术职业学院，河北 承德067000）

《机械与电气识图》是中等职业学校电气、机电等专业的核心课程[1]。通过本门课程的学习使用学生基本熟悉机械图样与电气图样的识图方法，具备独立解读零件图、装配图及电气图样的能力，为后续专业课程学习奠定基[1]。这门课程对学生的基本要求是能够已知三视图中的两视图，绘制第三视图或轴测图。要想绘制出第三视图或轴测图就需要想象构造物体工件的实际形状。学生可以在头脑中想象出物体的形状构造，但容易遗忘，一些图线不能准确呈现。最好的办法是粗画出物体工件的轴测图。掌握这项技能不仅能够准确画出工件的三视图，轴测图的绘制也迎刃而解。粗画轴测图的办法为构造组合体提供清晰的分析思路和设计依据，有迹可循，学生便于掌握。

1 已知三视图中的两个视图，画第三视图

三视图是观察者从三个不同位置观察同一空间几何体而画出的图形，各视图的形状与观察者从相应位置看到的几何体的形状一样。可以综合三个不同位置（侧面）的信息从细节上刻画空间几何体的结构。这三个不同的侧面分别为正面、上面和左面。从正面看到的图称为主视图，从上面看到的图称为俯视图，从左面看到的图叫做左视图，我们将这三个视图统称为三视图。已知三视图中的两个视图要求绘制第三个视图，不仅要遵循“长对正，高平齐，宽相等”的规律，还需要想象粗绘出空间几何体的形状。通常我们用轴测图来反映空间几何体的形状。轴测图一般分为正等轴测图和斜二轴测图两大类。这里以正等轴测图为例，研究根据三视图中的两个视图，粗绘正等轴测图的一般方法。首先，在画轴测图之前，先画空间坐标系。空间坐标系的坐标轴X轴Y 轴Z 轴之间的夹角均为120°,画出的轴测图成为正等轴测图。X 轴Y 轴Z 轴间的夹角也可以是90°，135°，135°，这样绘制的轴测图称为斜二轴测图。轴测图就要画在上述的空间坐标轴中。接下来，给三视图也加上平面坐标系（X 轴和Y 轴），这样轴测图空间坐标系与三视图平面坐标系完全对应。

1.1 无底座切割类组合体

观看图1（a），通过主视图和左视图可以判断该组合体没有底座，而且可以看成是由长方体切割而成。

第一步，在空间坐标系里，利用X 轴Y 轴Z 轴与长方体的长宽高分别与平行。先画长方体的底面，分别以X 轴Y 轴作为长方形的长和宽，可以方便的画出长方体的底面长方形。然后分别以底面长方形的四个角为顶点做平行于Z 轴的直线，直线的长度均为长方体的高。再连接四个高的顶点就构成了如图1(b)所示长方体。

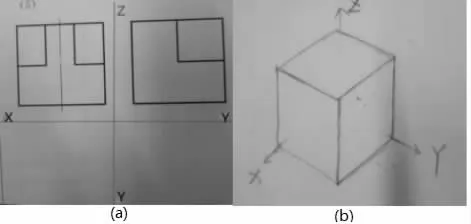
图1

第二步，根据主视图和左视图的形状画线切割组合体，如图2（a）所示。

第三步，擦掉切割掉的部分，将不清楚的线描实，就完成了轴测图的绘制，如图2(b)所示。

图2

最后，根据轴测图并结合三视图中另外两个视图，运用“长对正，高平齐，宽相等”的规律，即可准确画出第三个视图- 俯视图，如图3 所示。

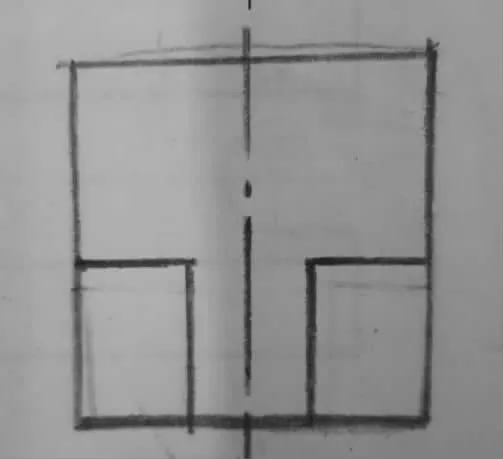
图3

1.2 有底座叠加类组合体

无底座组合体一般采用切割法绘制轴侧图，上面已经进行了讲解。有底座的组合体可采用底座优先法来绘制。已知如图4（a）所示的主视图和俯视图，如何绘制左视图？下面将详细说明。通过观察图4(a)所示的主视图，我们可以看出这是个有底座的组合体。同样需要先构造出空间几何体也就是绘制出轴测图。首先画轴测轴（空间坐标系），这里我们仍画正等轴测轴。接下来在空间坐标轴上画出组合体的底座，底座的画法与上述画长方体的方法相同。只是底座的高度较低，然后往上逐步画。观察图4(a)的俯视图，俯视图由一个大长方形和其内部两个小长方形构成，这两个小长方形内又分别有两道平行于Y 轴的竖线。我们可以分析出，大长方形就是底座的形状。这样底座就可以按照上面的方法画出。最后，在轴测图的底面上也画出这两个小长方形和里面平行于Y 轴的竖线。结合主视图来分析，可推断出底座上沿着Y 轴方向有前后两个长方体靠背。由于主视图斜线是实线，半圆是虚线，所以前面的靠背削成梯形，后面的靠背挖掉一个半圆。最后，画出了如图4(b)所示的轴测图。

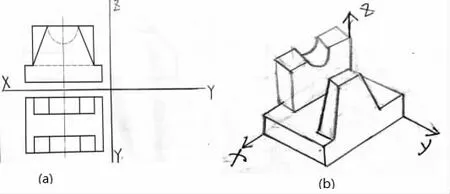
图4

2 已知轴测图画三视图

通过巧妙运用坐标轴，复杂的空间几何体可准确快速的被绘制出来。同样，已知空间几何体，也就是轴测图，通过加上坐标轴使三个侧面变得直观清晰，再来绘制三视图就会事半功倍。首先，给轴测图加上空间坐标轴。加坐标轴的一般原则是以组合体底面长方形里边看不见的边为X，Y 轴。由于坐标原点和坐标轴被组合体遮挡，在画坐标轴时只需要将坐标轴画在组合体的外边。这样，在视觉上就能呈现出空间三个投影面,如图5(a)。

在画三视图时，只需将轴测图分别向三个投影面分别做投影，由于三视图的坐标轴是轴测图的坐标轴沿Y 轴剪开展平后而形成的，所以三视图的坐标轴和轴测图的坐标轴是完全对应的。比如，画三视图中的主视图时，就要从前往后看，将整个组合体向XOZ 面做投影，那么在投影面上会呈现出一个长方形，较长的边平行于X 轴，较短的边平行于Z 轴，长方形里的两条竖线也平行于Z 轴。这样，可轻松的画出主视图，另外两个视图的画法也是类似的。因此通过轴测图绘制三视图是非常简单直观的，最后绘制出的三视图如图5(b)所示。

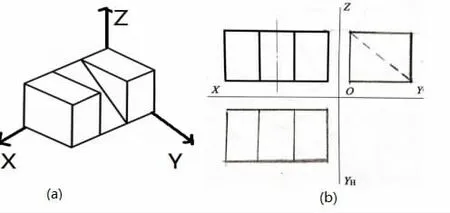
图5

3 总结——运用坐标轴绘图的好处

三视图与轴侧图的相互转化不仅是教学内容的需要，更是培养空间想象能力和空间构思能力的途径之一。画轴测图可以帮助人们构造几何体的直观形状特征，而三视图更有助于描绘几何体前后左右上下的细节。当然，对于特别复杂的工件，我们也可以采用剖视图或局部视图等来展示复杂细节，这里不再详细讲述。

运用坐标轴进行三视图与轴侧图之间的转化，有以下两点好处。

优点一：提高画三视图的准确度。轴测图上画空间坐标轴，在对应的平面坐标轴上画三视图不容易出现方向错乱，比如图5 中左视图虚线的方向容易画错，观察轴测图凹槽的方向分别与Z 轴和Y 轴倾斜相交，三视图中左视图的虚线也与Z 轴和Y轴倾斜相交。

优点二：提高画轴测图的速度和准确度。画轴测图时，先绘制坐标轴，整个立体图巧妙利用三个坐标轴，使轴测图的某些轮廓线与坐标轴重合，节省了画轮廓线的时间。同时轴测图横平竖直，斜线清晰明了，作图的准确度更高。如图5 所示。