基于仿真大光斑激光雷达和多层感知器的森林地上生物量估算模型构建

许昌建,刘迎春,左丽君,李建更,张 婷,韩路萌,方 宇,张 尹,王 天

(1.国家林业和草原局调查规划设计院,北京 100714；2.北京工业大学 信息学部,北京 100124；3.中国科学院空天信息研究院,北京 100094)

森林作为陆地生态系统的主体,其生物量占全球陆地生态系统生物量的80%[1],在减缓全球气候变化影响、维护生物多样性和防治水土流失等方面起到至关重要的作用[2]。森林地上生物量(Above-Ground Biomass,AGB)是评价森林生产力和固碳速率的关键参数,因此,快速准确地估测森林地上生物量对于量化碳储量和了解全球碳循环是十分重要的[3]。目前,各国通用的森林地上生物量估测方法主要基于大量样地调查数据和线性回归模型,虽然估测精度高,但需要耗费较大的人力、物力和财力[4]。随着遥感技术的不断发展,激光雷达(Light Detection and Ranging,LiDAR)能够穿透森林植被冠层,获取森林垂直结构信息,进而获得较高精度森林地上生物量[5-6]。联合星载激光雷达、机载激光雷达和地面样地数据的北美洲寒带针叶林地上生物量,估算结果与森林资源调查方法相差1.9%[7]。Muss等[8]利用小光斑激光雷达生成仿真大光斑激光雷达波形,对森林地上生物量进行估算,研究发现,仿真波形法能够构建与生物量高度相关的模型。

在生物量估测模型的构建方法上,大多数模型基于参数之间的线性关系构建。如，多元线性回归、偏最小二乘、数量回归等方法。由于遥感因子之间往往具有较强的非线性关系,导致这些方法的拟合效果不佳[9]。人工神经网络是一种模拟人脑神经元工作方式的建模方法,能够较好地拟合非线性关系,并且具有一定的自组织与自学习能力[10]。近年来,人工神经网络在林业上得到了愈发广泛的应用。例如，基于单隐含层反向传播(Backpropagation，BP)神经网络构建的遥感影像-森林地上生物量估测模型,在决定系数、均方根误差以及预测精度等方面均明显优于多元线性回归模型[11]；以2个隐含层的多层感知器和多元线性回归模型分别估算长白落叶松人工林地上生物量,证实了多层感知器的优势[12]。

尽管人工神经网络已用于森林地上生物量估测,然而目前的人工神经网络大多是浅层神经网络,即隐含层数较少。相关研究表明,与浅层神经网络相比,基于多隐含层的人工神经网络具有更强的表示能力,可挖掘出数据中更多的有用信息[13]。但更多的层数会带来更多的模型参数,需要更多的样本训练模型,而样地调查数据往往不能满足训练样本的数量要求。为解决训练样本不足的问题,本文利用机载激光雷达数据与样地调查数据建立回归关系,得到生物量样本数据,扩充了训练样本,用于多层感知器的训练。本研究以河北省张家口市为研究区域,利用小光斑激光雷达仿真大光斑激光雷达波形,进而提取波形参数,用于估算森林地上生物量,并比较了多元线性回归模型和多层感知器模型的估测精度和拟合优度。

1 研究区概况

研究区位于河北省西北部的张家口市,地理位置为39°30′～42°10′N,113°50′～116°30′E,属于温带大陆性季风气候区,四季分明,年平均气温6.2℃,年均降水量400mm。张家口市南北长289.2km,东西宽216.2km,下辖6区10县,土地面积3.68万km2,地势西北高、东南低,横贯中部的阴山山脉将张家口市划分为坝上、坝下两部分。坝上高原区海拔1 300～1 600m,地势平坦,草原辽阔,是典型的波状高原景观。坝下是华北平原和蒙古高原的过渡带,海拔500～1 200m,地形复杂,丘陵、河谷与盆地相间分布。研究区森林覆盖率61%,主要树种有落叶松(Larixgmelinii)、白桦(BetulaplatyphyllaSuk.)、油松(Pinustabulaeformis)、侧柏(Platycladusorientalis)、山杨(Populus

davidiana)、蒙古栎(Quercusmongolica)等。

2 材料及方法

2.1 数据获取

2.1.1机载小光斑激光雷达数据

机载小光斑激光雷达数据的采集时间为2018年9月15日—30日,天气晴朗。采用大疆经纬M600 Pro无人旋翼机搭载扫描鹰HS-600超轻小低空激光雷达系统,获取了9个1km×1km的小光斑激光雷达数据。因各个测区的面积较小且相对独立,调查时在每个测区的一级测量控制点上架设了一台地面基站。根据机载LiDAR航摄技术要求、测区范围、成图要求及HS-600航摄仪性能,制定了设备航飞参数(表1)。

表1 航飞参数

小光斑激光雷达分类。首先,采用噪声点滤波将明显低于地面的点或点群(低点)和明显高于地表目标的点,以及移动地物点归为噪点,最先分离出来。之后,使用LiDAR360软件对点云进行自动分类,再通过人工编辑,纠正自动分类时错分的点。最终分类后的激光雷达数据包含地面点、植被点、噪点3类(图1)。

图1 小光斑激光雷达分类流程

2.1.2样地调查数据

2018年9—10月在河北省张家口市调查了16个20m×30m森林样地。地面调查点的确定方法是:先在0.8m分辨率卫星影像和林地一张图上分树种、林龄组选择调查区域；之后,到调查区域选择备用调查点,并在卫星影像标记样地起始点和矩形样地范围,备用调查点一般选择有明确参考地物的地点；最后,调查人员从备选调查点选取最终调查样地,并提供准确的样地坐标。由于调查样地采用标志物定位,定位误差低于0.5m。由于无人机激光雷达数据位置精度高,且能够清晰分辨每一株树,调查样地与激光雷达数据间的匹配精度高于0.5m,能够保证二者位置的一致性。样地位置如图2所示。

图2 研究区和样地位置分布图

这16个样地按森林类型分为:针叶林12个和阔叶林4个；按林龄组分为:幼龄林3个、中龄林7个和成熟林6个。调查每个样地的经纬度、海拔、坡度,通过每木检尺获得样地林木的平均胸径,选取标准木,测量标准木树高,采用已发表的异速生长方程(表2)计算标准木生物量,并换算成样地生物量。用LAI-2200沿样地对角线测定森林冠层叶面积指数(LAI)。

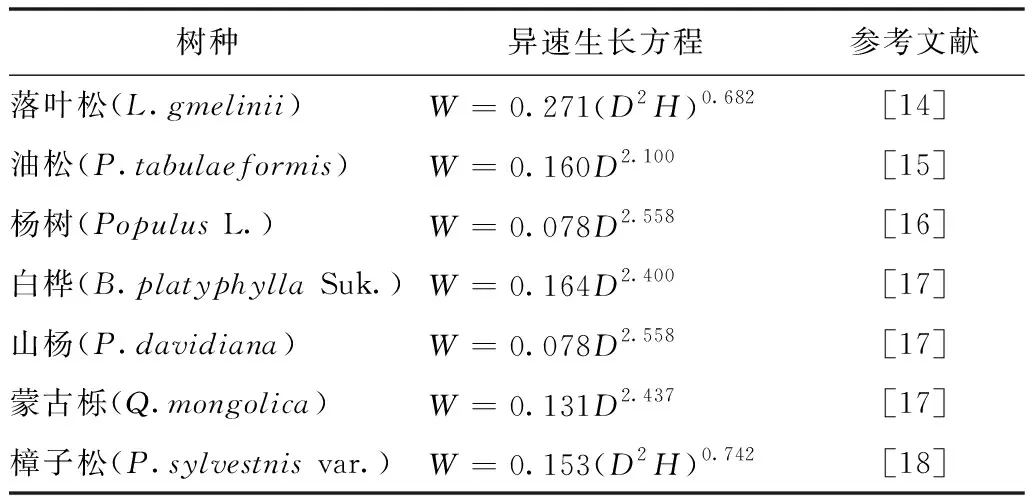
表2 主要树种生物量异速生长方程

2.2 波形仿真及其参数提取

仿真波形按照以下4个步骤生成:

1) 提取直径20m内的小光斑激光雷达,在垂直方向上以0.15m间隔对小光斑激光雷达进行高度划分。

2) 对小光斑激光雷达的反射强度赋予权重。一般来说,大光斑激光雷达的光斑能量分布服从二维正态分布,即光斑中心能量最高,向外逐渐衰减,光斑边缘的能量为中心能量的1/e2[19]。点云反射强度的赋值公式见式(1):

(1)

式中:Iw,i是第i个点加权强度；Ii是该点的反射强度；xi和yi是该点的平面坐标,x0和y0是光斑中心位置的平面坐标；R是光斑半径。

3) 对每个高度区间内的所有点的加权强度进行累加,得到初步的仿真波形。

4) 根据仿真波形能量的最大值和最小值,对仿真波形进行归一化处理,使其相对强度分布在(0,1)区间,得到归一化的仿真波形(图3),以降低点云密度对仿真波形的影响。

图3 归一化后的仿真大光斑激光雷达波形

提取仿真波形参数。本文提取了波形高度百分位数Qx(x=10,20,25,30,40,50,60,70,75,80,90,95)、波形内平均高Avg、波形内最大高Max、波形变异系数CV和波形标准差SD共16个波形参数(表3)。

表3 波形参数定义Tab.3 Definition of waveform parameters

2.3 样本处理

深度学习模型所需的训练样本较大,样地调查数据远不能满足训练样本的数量要求。为了扩充训练样本,本文以叶面积指数与冠层高度的乘积为自变量,建立与实测样地生物量关系方程；进而以此方程推算小光斑激光雷达覆盖区域的森林生物量,共提取1 333组生物量样本,且两两样本之间的距离大于50m。将样本数据按照4∶1的比例,随机地将样本划分为训练集和测试集,其中训练集1 068组数据,测试集265组数据。

2.3.1叶面积指数

叶面积指数(Leaf Area Index,LAI)是单位地表面积上所有叶片表面积的一半,是表征植被冠层结构的基本参量之一[20]。本文采用小光斑激光雷达结合样地实测叶面积指数计算区域森林叶面积指数。

叶面积指数的计算[21]如式(2)所示:

(2)

式中:ang为平均扫描角；GF为间隙率(Gap Fraction)；k为消光系数,消光系数由比尔-兰伯特方程得到。已有研究表明,大部分森林的消光系数可以为0.5[22]。

平均扫描角(ang)的计算如式(3)所示:

(3)

式中:n是小光斑激光雷达总点数,anglei是第i个点的扫描角度。

间隙率(GF)的计算如式(4)所示:

(4)

式中:nground是高度值低于高度阈值的地面点数。

2.3.2冠层高度模型

冠层高度模型(Canopy Height Model,CHM)由数字表面模型(Digital Surface Model,DSM)与数字高程模型(Digital Elevation Model,DEM)做差得到。本文所使用的DSM和DEM均由分类后的点云数据,在LiDAR360软件中,通过TIN插值法生成。插值时,采用逐点插入法构建Delaunay三角网,从最近的临近点组成的多个三角形共同形成的表面上提取栅格单元值。

2.4 估测模型

2.4.1多元线性回归模型

在森林地上生物量估测的相关研究中,多元线性回归(Multiple Linear Regression,MLR)模型的应用十分广泛[23],一般以森林地上生物量实测值作为因变量,以遥感数据参数作为自变量,通过一次多项式构建模型,拟合自变量与因变量之间的关系(式(5)):

Y=βX+ε

(5)

式中:Y表示地上生物量；X表示自变量；β为自变量的参数；ε为误差项。

2.4.2多层感知器模型

多层感知器(Multi-Layer Perceptron,MLP),也称作深度前馈网络,是一种典型的深度学习模型[24]。多层感知器的结构一般最左侧为输入层,中间为隐含层,最右侧为输出层(图4)。在多层感知器中,前一层的每个节点与相邻后一层的每个节点都是连接的,前一层接收的输入通过矩阵运算和激活函数后输出,作为相邻后一层的输入,并逐层运算至输出层。

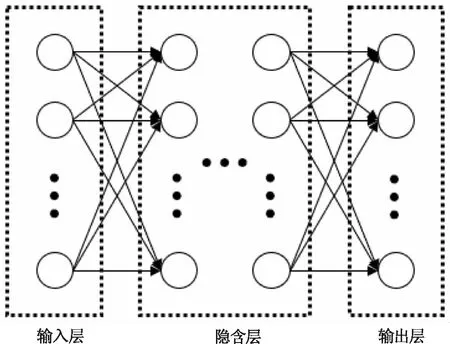
图4 多层感知器结构示意图

(6)

式中:激活函数σ(·)为修正线性单元(Rectified Linear Unit,ReLU),其表达式为:

σ(x)=max{0,x}

(7)

本文构建的多层感知器包含5个隐含层,每个隐含层均包含10个神经元,输入层神经元个数与输入变量个数相等,输出层有1个神经元。使用803组训练样本,学习率0.05,对模型训练1 000轮,并使用265组验证样本,对模型的拟合优度和估测精度进行评价。

2.4.3模型精度评价指标

本文从拟合优度和估测精度两方面对模型进行评价。评价拟合优度的指标为决定系数(R2)和调整决定系数(Adj.R2),公式如下:

(8)

(9)

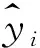
评价估测精度的指标为均方根误差(RMSE)、相对均方根误差(RMSEr)和平均绝对误差(MAE)作为,公式如下:

(10)

(11)

(12)

式中:n为样本总数；ymax为样地调查生物量最大值；ymin为样地调查生物量最小值。

3 结果与分析

3.1 叶面积指数计算结果

由小光斑激光雷达计算的叶面积指数(LAI),与样地调查叶面积指数(LAI′)存在较强的线性关系:LAI′=0.893LAI+0.192,R2达到0.94(图5)。以上述关系方程对叶面积指数进行修正,得到最终的区域叶面积指数产品,并与0.2m分辨率正射影像对比(图6)。叶面积指数产品的空间分布与影像中植被分布趋势一致:植被茂密区域的叶面积指数明显高于植被稀疏区域,无植被区域的叶面积指数为0(颜色越深表示LAI值越高,0值区域为白色)。

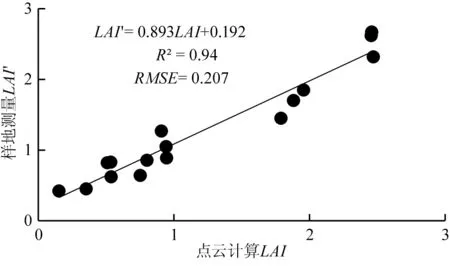
图5 小光斑激光雷达计算叶面积指数与样地测量叶面积指数对比

图6 测区叶面积指数与正射影像对比

3.2 生物量样本计算结果

以校正后叶面积指数(LAI＇)与冠层高度(H)的乘积为自变量,与样地生物量(B)建立回归关系(式(13)):

B=6.866×H×LAI＇+2.654

(13)

式中:H从CHM中提取，R2达到0.87(图7)。

图7 样地地上生物量与校正后叶面积指数(LAI＇)与冠层高度(H)乘积的关系

3.3 波形参数相关性分析

从波形参数间相关关系(图8)可以看出,高度分位数Qx之间的相关性较高,且分位数越相近,相关系数越大；而波形平均高Avg、波形变异系数CV和波形标准差SD与其他各项参数之间的相关系数较低,相关系数均小于0.4。

由于高度分为数Qx之间的相关性较高,本文分别以Q25,Q50,Q75,Q95,Max,AVG,CV,SD单个参数进行建模,评价了单个参数对模型估测效果的影响；同时对上述参数以一定方式进行组合,观察了不同参数组合的模型估测效果；最后用全部16个参数进行建模,从而比较多层感知器和多元线性回归模型对参数信息的挖掘能力。

3.4 多元线性回归估算生物量

首先建立单变量线性回归模型,观察单个波形参数与森林地上生物量之间的关系,模型的输入参数有高度百分位数Qx(x=10,25,50,75,95)、波形最大高Max、波形平均高Avg、波形变异系数CV和波形标准差SD。

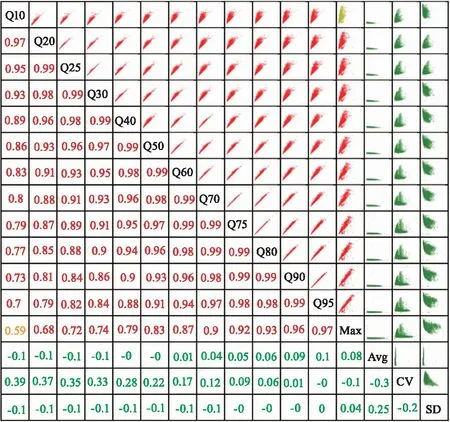
注红色表示相关系数绝对值大于0.6,黄色表示相关系数绝对值在0.4与0.6之间,绿色表示相关系数绝对值小于0.4,相关系数绝对值的数值在矩阵下半三角中列出。

表4 单变量线性回归模型参数及拟合效果

当采用单个波形参数作为输入时(表4),选择波形最大高Max得到的估测效果最好。以高度百分位数Qx作为输入变量时,x值越大,模型的估测效果越好。波形平均高Avg、波形变异系数CV和波形标准差SD与森林地上生物量的相关性较差,R2只有0.01。

在构建多元线性回归模型时,选取不少于3个波形参数,且尽量避免关系较弱的参数,建立多元线性回归模型(表5)。

各多元线性回归模型的评估指标见表6竖线左侧。可以看出,当参与建模的变量增多时,模型的拟合效果得到提升,选择全部16个变量进行建模时,模型的决定系数与调整决定系数均为0.60。

3.5 多层感知器估算森林生物量

表6中竖线右侧列出了各个多层感知器模型的拟合优度与估测精度,为了使比较结果更直观,估测结果更优的指标用黑体表示。

表5 13种波形参数组合得到的多元线性回归模型

表6 基于13种波形参数组合的多元线性回归模型和多层感知器模型估算森林地上生物量效果比较

从训练集与验证集的均方误差(图9)可以看出,在前80轮训练中,模型在训练集和验证集上的均方误差迅速下降。在第80到200轮训练中,模型在训练集上的均方误差缓慢下降,但在验证集上的均方误差并不稳定。在200轮训练之后,模型在训练集上的均方误差缓慢下降,在验证集上的均方误差逐渐稳定,不再随训练轮数的增加而下降。训练完成后,模型在训练集与验证集上的均方误差相差不大,没有出现明显的过拟合。

从表6可以看出,使用相同的变量组合进行建模时,除参数组合2中多元线性回归模型的RMSE和RMSEr优于多层感知器模型外,其余各项评价指标多层感知器模型均优于多元线性回归模型。

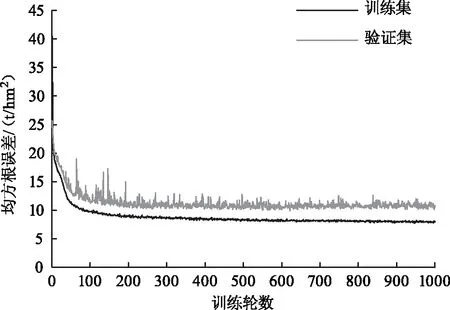
图9 多层感知器(参数组合12)估算地上生物量的均方根误差随训练轮数变化趋势

当参与建模的参数增加时,多元线性回归模型和多层感知器模型的估测效果均得到提升。但随着输入参数的增多,多元线性回归模型的估测效果得到的提升越来越有限,参数组合12比参数组合13的建模参数多7个,但多元线性回归模型估测结果的决定系数相同,其他评价指标也相近。从参数组合9,10,11,12和13看出,随着建模参数的增加,多层感知器模型的估测效果能够得到持续的提升,说明多层感知器模型的拟合能力更强,能够从新增的参数中挖掘出更多的信息。

以参数组合12为例,对多层感知器模型和多元线性回归模型估测16个样地地上生物量的结果进行对比。对多元线性回归模型而言,估测的生物量均值为48.46t/hm2,比实测均值51.52t/hm2低5.93%(图10(a))。6个样地的预测值比调查值高,10个样地的预测值比调查低,偏差幅度为-34.96～23.28t/hm2(图10(b))。对多层感知器模型而言,估测的生物量均值为49.43t/hm2,比实测均值低4.06%(图10(c))。6个样地的预测生物量比调查值高,10个样地的预测生物量比调查值低,偏差幅度为-19.09～20.19t/hm2(图10(d))。因此,多层感知器的预测结果比多元线性回归模型更接近实测值。

4 讨论与结论

本文利用样地数据和小光斑激光雷达数据扩充生物量样本,进而以小光斑激光雷达仿真大光斑激光雷达。虽然这会引入一些误差，但由于很多区域无法同时获取样地数据和大光斑激光雷达数据,可以将机载小光斑激光雷达数据作为样地数据与大光斑激光雷达数据的中间尺度数据。本文以仿真大光斑激光雷达波形参数作为模型输入参数,对比了不同参数组合的多元线性回归模型和多层感知器模型的森林地上生物量估测效果。实验发现,以单个参数构建模型时,波形最大高Max的估测效果最好。以高度百分位数参数Qx作为模型输入参数时,x的值越大,模型的估测效果越好。波形平均高Avg、变异系数CV和标准差SD作为参数时,模型的估测效果不好。

通过对比多元线性回归模型和多层感知器模型发现,当建模参数较少时,通过增加建模参数,两种模型的生物量估测效果均可得到提升。但参与建模的参数较多时,多元线性回归模型已不能够通过增加建模参数来明显提升估测效果,而多层感知器模型仍然能够从增加的参数中挖掘信息,提升模型的估测效果。当两种模型的建模参数相同时,多层感知器模型的拟合优度与估测精度显著高于多元线性回归模型。

本文工作也存在有待完善之处。样本数据由样地实测数据建立回归关系而得到,这样做虽然大大扩充了训练模型的样本,使训练多层感知器模型成为可能,但由样地实测数据到样本数据的转化中,可能引入新的误差,并对模型的估测结果产生影响,这种影响有待进一步的研究和分析。

目前,一些学者联合Lidar、可见光、高光谱、SAR等数据,对森林地上生物量进行估测,发现能够获得更好的生物量估测效果,这些数据特征提取和多源数据融合方式,对本研究的建模参数提取具有一定指导意义。未来应尝试更加多样的参数组合,将不同数据源的遥感数据进行融合,进一步提高模型的生物量估测能力。