数字散斑特性对三维重建精度的影响分析*

林旭华，陈新度，吴 磊

(广东工业大学机电工程学院，广州 510006)

0 引言

从真实世界的图像中重建物体一直是计算机视觉的核心问题之一[1]，而基于结构光的双目视觉三维重建技术能够充分的提高待测物体的重建精度。该方法通过对待测物体投射特定的结构光，利用双目视觉立体匹配的原理，对拍摄的二维图像进行立体匹配，获取待测物体的三维空间信息。因为该方法是一种具有非接触性、速度快、可靠性高、精度高的主动测量方法，目前被广泛应用于无人驾驶、无人机避障、医学诊断和逆向工程等热门领域[2-4]。

目前常用的结构光三维重建方法中，常用面结构光方法，也叫编码结构光方法，该方法不像点结构光与线结构光一样需要一个复杂的扫描机构扫描覆盖整个待测物体表面，而是通过直接投射特定的编码图像覆盖待测物体表面，从而获取高精度的三维信息。基于面结构光的三维重建方法中，常用的方法有条纹投影重建方法以及散斑投影重建方法。条纹投影重建方法具有立体重建处理精度与处理效率上的综合优势，但是需要对待测物体投影多幅图像进行编码，多用于静态物体的三维重建[5]。散斑投影重建方法只需要对待测物体投影单幅散斑图像，利用数字散斑相关方法获取同名点进行三维重建，该方法在快速动态成像的测量过程中更具有优势。

最初的数字散斑相关方法(DSCM)是由Yamaguchi和Peters W H等在二十世纪八十年代初分别独立提出的[6-7]。主要通过摄像机获取散斑调制过的待测物体图像，利用散斑相关算法确定图像上每个像素点上的视差值，再根据视差使用三角测量法获得待测物体的三维空间信息[8]。还有通过改进数字相关的搜索方式、改进相关系数计算模型、减小同名点搜索范围以及采用GPU并行加速计算流程等方法提高了计算精度和提高计算速度。唐家福等将布谷鸟算法引入数字散斑相关方法中，有效测量了刚体的位移量[9]。Cheng J等利用哈希方法在保证精度的情况下大幅度提高三维重建的图像匹配的速度[10]。

本文主要通过散斑质量理论分析以及三维重建实验，研究不同直径、灰度和分布特性的单幅投影散斑图像对双目三维重建精度的影响。

1 基本原理

1.1 双目立体视觉重建原理

双目立体视觉重建的原理来源于人类的双目视觉系统[8]，通过采用两个相同的相机模拟人的双眼，在不同视角采集同一位置下的待测物体两侧图像，利用立体匹配方法在图像对中搜索同名点求取待测物体的视差，获取待测物体的三维信息，从而完成物体的三维重建。

图1所示的是一个理想的双目相机模型。基于双目视觉的三维重建要获得物点P的深度信息Z。因此先通过相机标定以及先验信息，获取相机焦距f，确定左右相机基线距离B以及双目相机分别采集到的左右成像点视差d=xl-xr。其中cleft,cright为左右侧视图的坐标轴的主点。

图1 双目视差原理

如式(1)所示，利用三角几何关系可得物点P的深度信息。

(1)

通过双目相机标定获得的重投影矩阵Q进一步计算物点P的三维坐标。

(2)

式中，(cx,cy)为左相机图像的主点，f为相机焦距，cx′ 为右相机图像x坐标轴主点，Tx为两幅立体图像平移向量在x方向上的分量。利用重新投影矩阵Q可以将给定屏幕坐标和摄像机内参矩阵的二维点重新投影至三维。

(3)

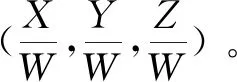
1.2 数字模拟散斑原理

近年来，越来越多地将散斑的特点应用于三维重建领域，取得了良好的效果。散斑图有多种生成方法，其中通过计算机模拟生成的散斑图案可以人为的设置散斑直径、散斑数量、散斑分布随机度以及灰度等关键参数，适用于不同的实验环境。

计算机模拟散斑是在Matlab上根据高斯分布的规律模拟散斑生成[11]，函数可表示为：

(4)

式中，(u,v)为图像坐标轴主点，S表示散斑点的数量，I0表示图像背景的光强，a表示散斑点的直径大小，(uk,vk)点表示第k个散斑点的中心位置。可以模拟出以下两种类型的散斑图像。如图2、图3所示。图4为二值灰度局部散斑。

图2 随机灰度全局散斑 图3 二值灰度全局散斑

图4 二值灰度局部散斑

图2散斑点灰度值范围为0～255，图3斑点灰度值二值化，两幅图像散斑点均随机分布，且有部分散斑的重叠。

针对散斑点重叠这个问题，对散斑图像的中心点分布进一步优化，将整幅散斑图像划分为固定大小的p×q个区域，在每个小区域随机分布1个数字散斑，生成一种二值灰度局部散斑，这样的散斑中心点位置将被固定在一个范围区域内，大幅度避免了斑点重叠，而各区域随机选取中心点也保证了散斑分布的均匀性与随机性。

1.3 数字散斑相关方法

本文介绍与采用的则是半全局立体匹配算法SGBM算法[12-13]。该算法的核心思路为：通过固定左相机图像的一个像素点，在右图像上搜索同名点，得到像素点的视差，生成视差图。设置一个和视差图相关的全局能量函数，使能量函数最小化，以达到求解每个像素点最优视差的目的。能量函数式(5)如下所示：

E(D)=∑p(D(p,Dp)+∑q∈NpP1I[|Dp-DQ|-1]+

∑q∈NpP2I[|Dp-DQ|>1])

(5)

式中，E(D)为视差图像对应的能量函数，D为视差图像；p，q为图像的某个像素点；Dp与Dq表示像素点p，q的深度值。Np指像素点p周围连通的八个像素；D(p,Dp) 指像素点p的深度值为Dp时的匹配代价；平滑惩罚系数P1作用于与像素点p连通的八个像素中与点p生深度值相差为1的像素，而平滑惩罚系数P2作用于深度值相差大于1的连通像素。I[…]为布尔型变量。

SGBM算法通过在多个方向上的一维路径的约束来近似二维约束，在每个方向上按照动态规划的思想进行能量累积，然后将各个方向上的匹配代价相加得到总的匹配代价，当前路径代价累计式如下所示：

Lr(p,d)=C(p,d)+

min(Lr(p-r,d),Lr(p-r,d±r)+P1,

(6)

式中，r表示指向当前像素p的方向，Lr(p,d)表示沿着当前方向，当像素为p，深度值为d时的最小代价值。k,i均为视差值。

将所有搜索方向的匹配代价相加得到代价即为总的匹配代价，如下式：

s(p,d)=∑rLr(p,d)

(7)

再通过亚像素插值提高匹配精度。唯一性检测、左右一致性检测与连通区域检测，灰度约束，排除误差点。选取代价最小的视差值作为该像素点的最终视差值。圆柱体扫描图见图5。利用SGBM算法即可生成视差图，如图6所示。

图5 圆柱体扫描图 图6 圆柱体视差图

2 散斑图质量分析

散斑的质量是提高重建精度的关键，通过合适的散斑质量分析方法筛选高质量的散斑图对提高重建精度有着极大的意义。

2.1 直方图分析

散斑图的质量分析方法有很多，汤其剑等围绕散斑相关系数计算和亚像素同名点插值精度重点分析散斑图的三维重建效果，得出了二值灰度散斑优于随机灰度散斑的结论[14]。潘兵等提出了一种平均灰度梯度来描述散斑图质量的方法[15]。

散斑的直方图分布也带有图像的特征信息，通过观察图像的直方图以及不同灰度区间的像素分布也可判断图像的质量。散斑灰度直方图中灰度分布越均匀，则代表模拟的散斑随机性越好。上文模拟的散斑图像的灰度直方图，如图7所示。

(a) 随机灰度散斑灰度直方图

图7a为随机灰度散斑图案，直方图中像素分布明显不均匀。图7b、图7c分别为二值灰度全局散斑与二值灰度局部散斑，像素分布较为均匀。

2.2 平均灰度梯度分析

根据散斑图不同的灰度分布特征，从子区灰度平方和出发，提出一个新的全局参数：平均灰度梯度d，用于平均整个散斑图的质量，定义如下：

(8)

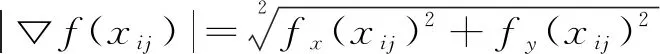
通过计算可以得到整幅散斑图像的平均灰度梯度，推出x方向的灰度梯度平方和近似表达式：

(9)

N为图像子区大小，由上式可知图像子区越大，式(9)的近似结果就越准确。并且由式(9)可得到模拟散斑图案的位移测量精度及精度都和散斑图案的平均灰度梯度和子区大小N的乘积成反比。而平均灰度梯度是散斑图的统计参数，当图像的噪声方差、图像子区的大小和插值方法确定后，该参数与测量结果唯一相关，由此可作为评价散斑质量的有效参数。

针对上述模拟散斑图进一步计算它们的平均灰度梯度，如表1所示。

表1 模拟散斑图平均灰度梯度

当平均灰度梯度较大时，散斑数字相关方法测量结果的均值误差和标准差将会有更好的表现。随机灰度的平均灰度梯度结果较大，而直方图分布却不均匀，因此进一步设计三维重建实验，分析散斑图灰度特性对重建效果的影响。

3 实验与分析

3.1 实验设计

通过上述分析，设计实验判断投影散斑图像类型对三维重建质量的影响。实验型号为UI325xcp-C，200万像素。投影仪型号为DPL-600W，分辨率为1280×800，如图8所示。检测物体为标准量块。

图8 实验装置图

设计实验，对标准量块的中心位置进行重建。使用不同类型的散斑投影图像，并散斑直径进行调整，分析不同散斑大小对重建效果的影响。设置散斑直径大小为1 pixel×1 pixel、2 pixel×2 pixel直到9 pixel×9 pixel共9组。如图9所示。

(a) 直径为1pixel (b) 直径为2pixel

分别选择3 pixel ×3 pixel、5 pixel ×5 pixel直至11 pixel ×11 pixel大小的SAD代价窗口，得到45个重建表面。

3.2 实验分析

分别对45个重建表面计算拟合的残差标准差。结果如图10、图11所示。

图10 量块拟合残差标准差分布

图11 量块拟合残差标准差由小到大排列

通过图10和图11对标准量块的重建结果可以得知。当散斑直径较大而窗口较小时，拟合误差较大。用以匹配的窗口内获取的散斑特征单一，将导致较多的误匹配点，使误差增大。

通过灰度约束判断误差点的过程中，由于随机灰度散斑的散斑灰度值为0～255，而二值灰度散斑只有0与255两个灰度。在SAD窗口较小，而散斑直径较大时，随机灰度散斑因为灰度差异不符合灰度阈值被排查掉的误差点将会比二值灰度散斑多。此时随机灰度散斑的匹配效果会比二值灰度散斑的好。但是随着窗口的增大以及散斑直径的减小，量块平面的拟合精度将会越来越高。

由图11可知在散斑直径小且SAD窗口大时，二值局部散斑的匹配效果比随机灰度散斑与二值全局散斑的效果好，标准差最小达到了0.013 4 mm。

在实际应用中，采用实验验证效果最佳的二值灰度局部散斑辅助照明，设置散斑直径大小为1 pixel，SAD窗口大小为11 pixel的最优参数，对粗糙的陶瓷罐进行表面重建。虽然在遮挡、边缘区域有少部分数据缺失，但是可以成功还原复杂物体表面的三维信息，实现了19万个点的稠密重建，系统重建效果如图12所示。

图12 陶瓷罐三维重建点云效果

通过量块平面的重建对比实验可知，二值局部散斑具有更好的随机性，更低的斑点重叠率。在寻找同名点的过程中能够较为准确的寻找同名点以及排除误差点。在散斑直径较小，SAD窗口较大时，二值局部散斑的辅助效果最好，精度最高。

4 结论

本文重点研究了基于计算机散斑的三维重建方法，包括双目视觉系统模型，同名点的搜索匹配方法，不同类型的模拟散斑图生成方法。通过直方图与平均灰度梯度重点分析比较了随机灰度散斑、二值全局散斑与二值局部散斑的重建效果。并设计在不同的散斑直径与SAD窗口的实验条件下，对标准量块进行了三维重建实验比较，针对本文系统，得出了在散斑直径为1～2 pixel大小，窗口大小为11 pixel时，重建效果最好且二值局部散斑的重建精度优于随机灰度散斑与二值全局散斑，为基于计算机模拟散斑的三维重建系统设计提供了参考。