基于改进粒子群算法的发动机曲柄连杆机构优化*
2021-03-26刘清华陈家兑
刘清华,陈家兑
(贵州大学现代制造技术教育部重点实验室,贵阳 550025)
0 引言
发动机的曲柄连杆机构是发动机重要的运动机构,其结构及参数直接影响着其运动状态,进而影响发动机的性能。为此,许多学者对发动机的曲柄连杆机构的优化设计开展了相关研究。文献[1-3]提出了在曲柄滑块机构工作中多维优化设计模型。唐承等[4]利用模拟退火算法对发动机曲柄连杆结构进行可靠性分配优化,获得了更加合理的结果。黄保科等[5]对发动机曲轴轴承进行了多目标综合优化,结果表明轴承的总摩擦功耗和曲轴质量都相对于单目标优化设计结果有进一步的减少。发动机工作时,活塞在气缸中作往复运动,会产生很大的往复惯性力,不仅使连杆系统的零件承受附加的周期性载荷,而且容易导致曲柄连杆机构出现运动不平衡而降低发动机性能[6]。其中,尺寸参数是影响曲柄连杆机构往复惯性力的重要因素。因此,可以通过优化曲柄连杆结构尺寸而减小曲柄连杆机构往复惯性力。
本文拟在建立发动机曲柄连杆机构动力学模型的基础上,引入粒子群优化算法(particle swarm optimization,PSO)建立发动机曲柄连杆机构在约束条件下受力分析的优化设计数学模型,实现曲柄连杆机构的优化。
1 发动机的曲柄连杆机构受力分析
发动机曲柄连杆机构由活塞、连杆、曲轴组成,其机构简图如图1所示。
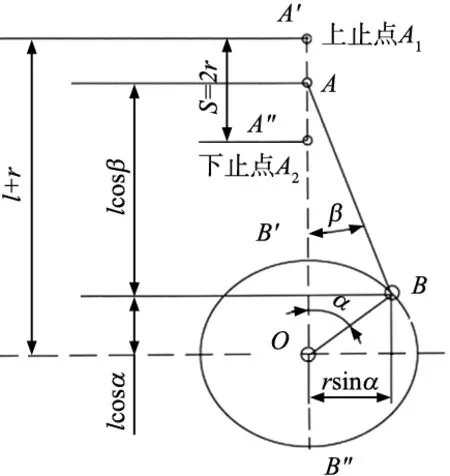
图1 发动机曲柄连杆机构简图
根据图1中各参数的数学关系将活塞位移表示为:
(1)
将曲轴旋转看做匀速,则式(1)可以写成:
(2)
其中,r为曲轴半径(m);α为曲轴转角(rad);ω为曲轴角速度(rad/s);t为运动时间(s)。
将式(2)中的位移对时间求导,可得活塞速度为:
(3)
其中,v为活塞速度(m/s)。
将式(3)中的速度对时间求导,可得活塞加速度为:
(4)
其中,a为活塞加速度(m/s2)。
为了方便分析,这里认为往复运动所有质量集中在活塞销上,质心是活塞销的中心,因此式(4)表示的活塞加速度可以认为是活塞销的加速度,即曲柄连杆机构中往复运动的质心加速度,可以得到往复运动所受的力为:
F=m1a
(5)
其中,F为往复运动所受作用力(N);m1为往复质量(kg)。
因此活塞系统往复惯性力可以表示为:
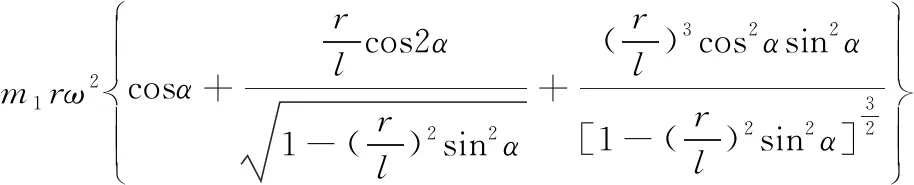
(6)
其中,F′为往复惯性力(N),该式表示机构运动产生的惯性力大小,方向时刻与加速度方向相反,因此往复惯性力会引发发动机震动,由于连杆运动是发动机振源控制的基础,在机构正常工作的条件下减少往复力的大小极其重要,这是一个多参数优化设计问题。在初始设计时,取l=0.16 m,F′的函数图像如图2所示,取r=0.045 m,F′的函数图像如图3所示。二者均为多极值多元函数,常规方法求解极值比较困难,因此,引入粒子群算法进行求解。
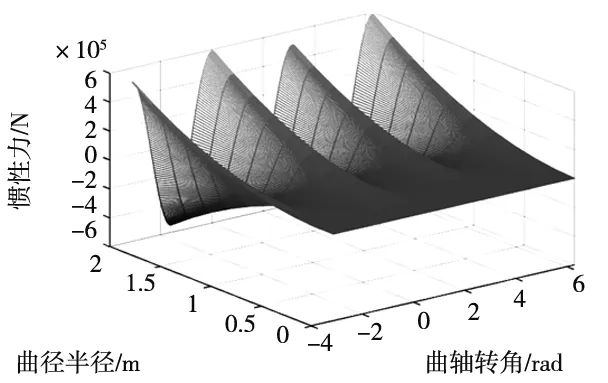
图2 惯性力图像(一)
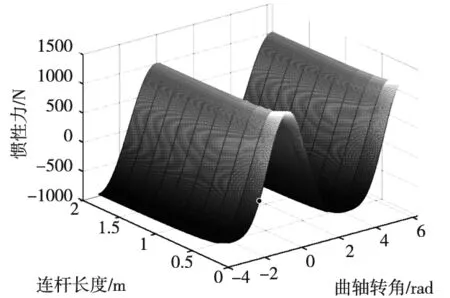
图3 惯性力图像(二)
2 基于粒子群算法的优化设计
粒子群优化算法(particle swarm optimization,PSO)是 Eberhart 和 Kennedy开发的一种模拟群体智能行为的优化算法[7]。采用惯性权重线性递减粒子群算法(LDIW)[8]通过对惯性权重的动态调整比普通粒子群算法具有更精细的搜索能力。粒子群优化算法作为一种进化算法(Evolutionary Algorithm,EA)具有进化计算和群体智能的特点,可以实现复杂空间最优解的搜索。利用粒子群算法在文献[9]中的一个多极值测试函数式进行优化计算可以得到较理想的结果。同时,PSO算法因其参数设置简单,容易实现、精度高、收敛快等特点,在文献[10]表明粒子群算法可用于优化设计。
2.1 粒子群算法基本原理
在粒子群算法中,每个优化问题的解被看做搜索空间的一个粒子,在算法开始时生成初始解,即在可行解空间中随机初始化N个粒子组成的种群X={X1,X2,...,XN},其中每个粒子所在的位置Xi={xi1,xi2,...,xin}都表示问题的一个解,以此根据目标函数搜索新解。在每次迭代中,粒子根据本身搜索到的个体极值pid和整个种群目前搜索到的全局极值pgd来更新自己。此外,每个粒子都有速度Vi={vi1,vi2,...,vin},当两个极值都找到后,每个粒子会由式(7)更新自己的速度。
vid=wvid(t)+η1rand()[pid-xid(t)]+η2rand()[pgd-xid(t)]
xid(t+1)=xid(t)+vid(t+1)
(7)
其中,xid(t+1)为第i个粒子在第t+1次迭代中第d维上的速度;w为惯性权重;η1、η2为加速常数;rand()为0~1之间的随机数。
在该算法中加入线性递减的权重,在搜索过程中可以对w进行动态的调整,采用线性递减权值策略,其表达式为:
(8)
其中,Tmax为最大进化次数;wmin为最小惯性权重;t为当前迭代次数。
在该算法中加入约束条件,保证粒子速度和个体都在约束范围内,即当vid(t+1)>vmax时,vid(t+1)=vmax;当vid(t+1)<-vmax时,vid(t+1)=-vmax;当xid>xmax时,xid=xmax;当xid 当发动机曲柄连杆机构的材料选定时,其设计方案由三个设计变量决定,即连杆长度l、曲柄半径r、曲轴转角α。故取设计变量为: Z=(z1,z2,z3)T=(l,r,α)T (9) 考虑到要使机体惯性力最小,因此优化设计目标函数为: (10) 考虑到连杆中的集成部件正常工作和为连杆长度、曲柄半径提供一个可变参数范围,据此建立约束条件为: 0.135 m≤z1≤0.145 m (11) 0.035 m≤z2≤0.039 m (12) 0≤z3≤2π (13) 综上所述,将所有约束条件规格化,可得发动机曲柄连杆机构优化设计的数学模型为: minf(z) g1(Z)=0.135-z1≤0 g2(Z)=z1-0.145≤0 g3(Z)=0.035-z2≤0 g4(Z)=z2-0.039≤0 g5(Z)=z3≥0 g6(Z)=z3-2π≤0 (14) 编写PSO算法程序对式(14)进行优化求解,这里取发动机转速为2000r/min,往复质量为活塞质量和连杆质量之和,PSO算法的初始参数设置如表1所示。 表1 粒子群算法初始参数 在MATLAB中的运行程序,求解结果如图4所示。 图4 算法收敛曲线 可以看出,该算法收敛速度较快,系统惯性力在迭代50次以内即达到了极值-627.59 N,在取到极值时得到解集Z为 : Z=(z1,z2,z3)T=(0.145,0.039,3.519 4)T 该机构在初始设计时为连杆长度l=0.160 m,曲柄半径r=0.045 m。如前所述,优化后的为连杆长度l=0.145 m,曲柄半径r=0.039 m。将优化前后的连杆长度、曲轴半径、发动机转速2000r/min分别代入式(1)、式(3)、式(4)、式(6),可得到优化前后速度、加速度和系统惯性力曲线,如图5~图8所示。 图5 优化前后活塞位移对比图 图6 优化前后速度对比图 图7 优化前后加速度对比图 图8 优化前后惯性力对比图 可以得到,在转速为2000 r/min时,优化前在曲轴转角为0 rad时正向惯性力最大,为1 298.95 N,优化后在曲轴转角为0 rad时惯性力力最大,为1 085.43 N,比原设计减少了约16.5%;优化前在曲轴转角为2.62 rad和3.67 rad时反向惯性力最大,为-728.70 N,优化后也是曲轴转角为2.62 rad和3.67 rad时获得最大反向惯性力,为-625.74 N,比原设计减少了约14.2%。 发动机的曲柄连杆机构的往复惯性力影响着发动机的震动及性能,通过智能优化算法的粒子群算法对曲柄连杆机构结构参数进行优化,获得良好的效果,使发动机曲柄连杆机构的最大正向惯性力减小16.5%,最大反向惯性力降低14.2%。结果表明,改进PSO算法收敛速度快,计算精度高,通过迭代实现对复杂函数极值的求解,对于机械优化设计展示了其优越性。2.2 建立优化设计数学模型
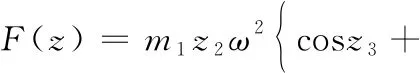
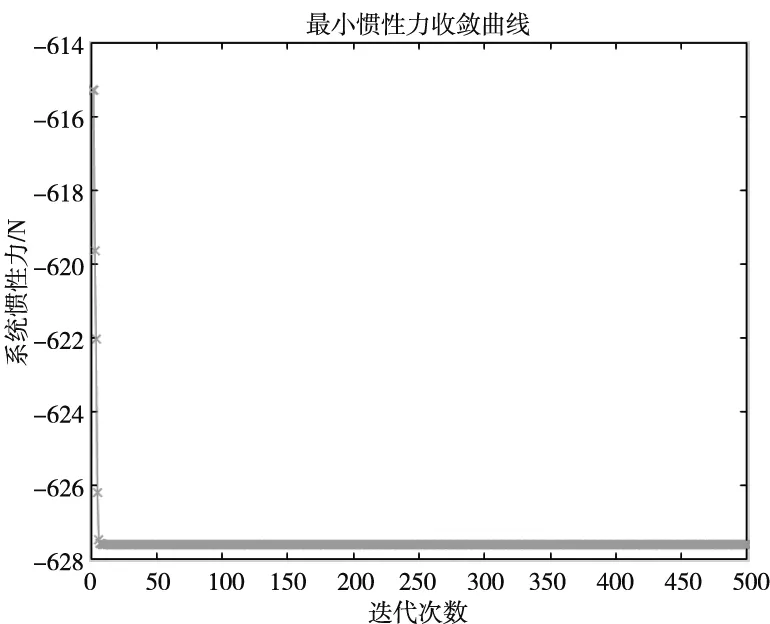
2.3 利用粒子群算法求解

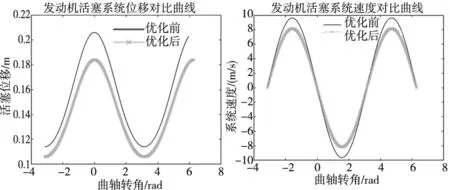
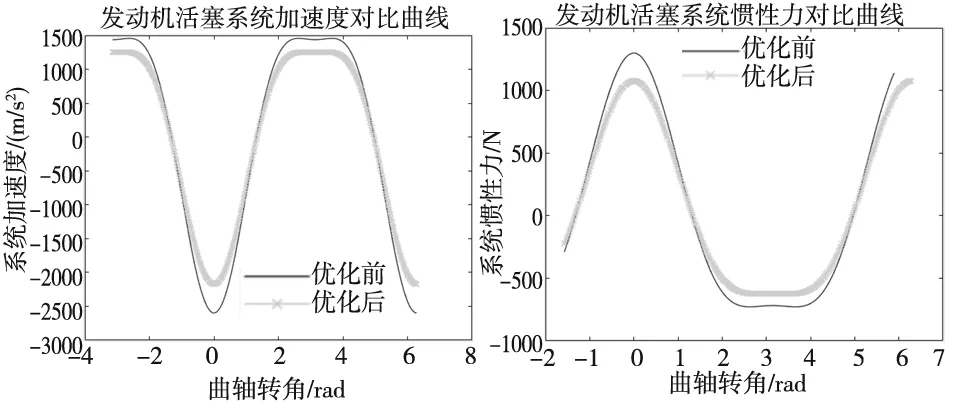
2.4 优化设计结果验证
3 结论
