参数不确定下的磁悬浮双转子系统的动态特性*

张辰川,王念先,王东雄

(武汉科技大学 a.冶金装备及其控制教育部重点实验室；b.湖北省机械传动与制造工程重点实验室, 武汉 430081)

0 引言

航空发动机中以电磁轴承(Active Magnetic Bearings, AMB)支承的双转子系统取代传统机械轴承支承的双转子系统，可显著降低系统的复杂程度，减轻发动机重量，优化发动机结构，以及获得更高的可靠性[1]，是未来高推重比、高性能的新型发动机的重要发展方向。

磁悬浮双转子系统作为未来新型航空发动机的关键组成部件，其动力学特性直接影响发动机的整体性能，而研究磁悬浮双转子系统的动力学特性关键在于AMB支承特性的确定。现有研究中，关于AMB的支承特性大多是通过电磁力模型获取AMB的位移刚度系数和电流刚度系数，进而获取控制系统的传递函数来得到AMB的支承等效刚度和阻尼[2]。赵雷等[3]通过建立PID控制算法下AMB的支承刚度和阻尼模型，并展开相关研究。但该方法只有在控制系统的传递函数确定时才可能对支承等效刚度和阻尼进行理论计算，对于传递函数不明确的非线性控制算法并不适用。Xu Y、Zhou J等[4-5]是基于已有对象展开，缺乏磁悬浮支承特性变化规律的系统描述，不能直接用来研究磁悬浮双转子系统的动力学特性。目前，由于鲁棒控制下的AMB的传递函数并不明确，无法建立AMB的支承刚度和阻尼模型，进而导致AMB支承特性的不确定性，而对于AMB存在支承特性不确定性的系统可以通过传统转子动力学中的不确定量化的方法对其展开研究。

针对传统转子动力学中存在不确定性问题的研究方法主要有概率方法[6-11]、模糊方法[12-14]和区间分析方法。其中，区间分析方法对系统不确定参数的概率分布和样本空间范围要求不高，适合于磁悬浮转子系统这种非随机过程系统的动力学响应特性分析。Qiu Zhiping,Qi Wuchao等[15-17]通过区间摄动方法分析不确定结构的动态响应，得到了很多有益的结论。方勃、王军等[18-19]用区间分析方法得到了固有频率随系统参数的变化关系，得出了转子临界转速的变化范围。Fu C等[20]通过四阶Magnus级数展开式的区间精细积分方法，分析了不同不确定性参数下单转子系统的瞬态响应。Ma Y等[21]通过区间数学和模态叠加算法分析了具有不确定但有界参数的转子系统动态响应范围。

可看出，利用区间分析法能有效的对存在不确定性的转子系统的动力学特性展开研究，但以上研究所采用的转子模型多为机械轴承支承的单转子模型。而磁悬浮双转子系统中，由于中介轴承的存在，内外转子间的动态耦合将十分严重，AMB支承特性的不确定性导致双转子系统的动力学特性更加复杂。因此，本文将区间法引入到磁悬浮双转子系统的研究中，将AMB支承特性的不确定性量转化为‘未知而有界’的区间，建立基于区间法的磁悬浮双转子系统的动力学模型，对存在支承特性不确定性的磁悬浮双转子系统的动力学特性展开研究，从而为磁悬浮双转子系统的应用奠定基础。

1 区间法建模

1.1 确定系统的动力学方程

多电航空发动机转子部件的核心多为一个复杂的磁悬浮双转子系统，为了对磁悬浮双转子系统展开研究，设计了一种永磁轴承和电磁轴承混合支承的磁悬浮双转子实验平台，其主要结构如图1所示，内转子和外转子通过两个永磁轴承(Permanent Magnetic Bearing，PMB)作为中介轴承实现耦合，外转子由两个AMB悬浮支承。外转子左端和内转子右端分别通过弹性膜片联轴器连接到两台高速电机上，允许一定的轴向偏移和角度偏转，从而可以调节内外转子的轴向自由度。

1、8. 中介轴承 2、7. AMB转子 3. 内转子 4. 圆盘2 5. 外转子 6. 圆盘3 9. 圆盘1

根据图1所示磁悬浮双转子系统的结构特点，采用考虑转动惯量和陀螺效应的Euler-Bernoulli梁元件来描述转轴，将内转子离散为12个节点，外转子离散为23个节点，并且将内外转子的圆盘视为刚性圆盘得到如图2所示的磁悬浮双转子系统的简化模型。图2中节点3和14与节点8和34所在的位置为中介轴承，节点19和节点30为AMB，节点10为内转子圆盘，节点23和26为外转子圆盘。

图2 磁悬浮双转子系统的简化模型

各刚性圆盘单元、弹性轴段单元和轴承单元的运动方程可参考文献[22]。由图2设内转子的广义位移矢量为：

(1)

式中，yk和zk(k= 1, 2, …, 12)表示内转子节点1～12的平动位移，θyk和θzk(k= 1, 2, …, 12)表示内转子节点1～12的转动位移。通过组装内转子上各轴段和圆盘的运动方程，可得内转子运动方程为：

(2)

式中，ML、JL和KL分别为内转子子系统的质量矩阵、陀螺矩阵和刚度矩阵，ΩL为内转子的旋转角速度，QL为作用在内转子系统的广义力，在这里只考虑因圆盘偏心距引起的不平衡力,则圆盘不平衡力Qd可表示为：

(3)

式中，fu为不平衡量，基于上式则QL可表示为：

(4)

式中，Qd1为内转子圆盘1的不平衡力。

同理，设外转子的广义位移矢量为：

(5)

其中，yk和zk(k= 13, 14, …, 35)表示节点13～35的平动位移，θyk和θzk(k= 13, 14, …, 35)表示节点13～35的转动位移。通过组装外转子上各轴段和圆盘的运动方程，可得外转子的运动方程为：

(6)

式中，MH、JH和KH分别为外转子子系统的质量矩阵、陀螺矩阵和刚度矩阵，ΩH为外转子的旋转角速度，QH为作用在外转子系统的广义力,在这里只考虑因圆盘偏心距引起的不平衡力,则可表示为：

(7)

式中，Qd2和Qd3分别为外转子圆盘2和圆盘3的不平衡力。

基于上述分析，并根据图2所示AMB和中介轴承的节点编号，将AMB和中介轴承的刚度和阻尼加入到刚度矩阵和陀螺矩阵中即可得到磁悬浮双转子的运动方程，磁悬浮双转子系统的动力学方程可表示为：

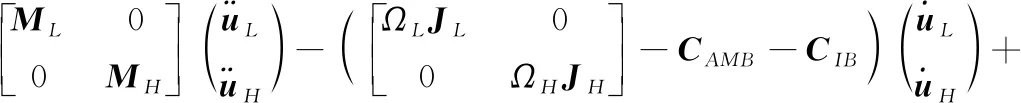
(8)

式中，CAMB和CIB分别为AMB的阻尼矩阵和中介轴承的阻尼矩阵，KAMB和KIB分别为AMB的刚度矩阵和中介轴承的刚度矩阵，具体形式可参考附录公式，为了简化方程和方便描述，将磁悬浮双转子系统的运动方程用下式表示：

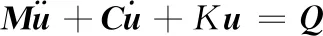
(9)

1.2 磁悬浮双转子系统的区间法模型

上述建立的是确定性的磁悬浮双转子系统运动方程。当传递函数不明确的情况下，蒋科坚等[23]通过在线测量方法得到了AMB的等效支承刚度和等效支承阻尼随频率变化的曲线。而通过该测量方法得到AMB的支承特性随频率的变化曲线相对复杂，在这种情况下，难以对AMB的支承特性进行定量化描述，这时，将AMB的支承特性的转化为‘未知而有界’的区间就显得尤为方便。

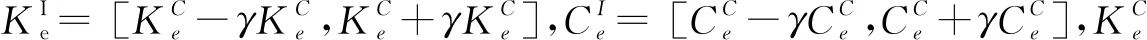
为考虑磁悬浮转子系统支承特性的不确定性，本节将引入Chebyshev正交多项式的区间分析方法。

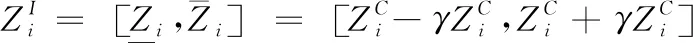
(10)

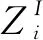
考虑不确定性的系统运动微分方程可表示为：

(11)

(12)

式中，u0为响应初值,uI为响应区间。这里采用Chebyshev正交多项式的区间分析方法来求解上式的响应区间,第一类Chebyshev正交多项式为：

Ck(x)=coskθ,x∈[-1,1]

(13)

式中，θ=arccos(x) ∈ [0,π]，k为非负整数。Ck(x)在x∈ [-1,1]上关于权函数ρ(x)=(1-x2)1/2正交。

Ck1,k2,···,kr(ZI)=cosk1θ1cosk2θ2···coskrθr

(14)

式(12)的响应解可用截断的n阶切比雪夫近似表示：

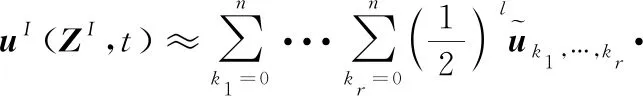
(15)

(16)

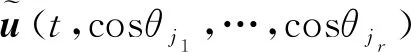
(17)

当不确定区间变量定义为在任意区间范围内时，可通过下式转化为标准区间：

(18)

2 区间法验证

区间法在传统转子动力学的应用已有大量研究，为了更好的把传统转子动力学上的区间法应用到磁悬浮转子系统的不确定问题上，首先为了保证区间方法的正确性与有效性，本小节将采用文献[20]中的模型进行验证，转子模型如图3所示，具体的确定物理参数可参考文献[20]。对图3的单转子进行恒定角加速度的瞬态响应进行研究，研究过程中将角加速度取为55 rad/s2，时间步长取为1 ms。在转子系统中求解响应的常用方法是Newmak-β法，本小节将采用Newmark-β法与Chebyshev区间分析方法相结合来验证区间模型的正确性。

图3 文献[20]的单盘悬臂转子模型

在对转子系统的分析和研究过程中总会遇到一些不确定性的因素，例如测量不精确，加工水平与条件等因素，导致结构的材料参数、几何特性和外荷载等实际存在的不确定性。对图3所示的转子，进行各个参数不确定下的瞬态响应研究,响应结果如图4所示。考虑转子系统不平衡量与轴承阻尼不确定参数下，单盘悬臂转子加速启动过程中的响应如图4a、图4b所示。转子系统的支承刚度一直难以精确定义，材料特性也处于分散状态，在这种情况下，考虑支撑1的刚度和杨氏模量的不确定性对转子系统的影响，响应结果如图4c、图4d所示。考虑轴内径与轴1的长度的不确定性对转子系统的响应结果如图4e、图4f所示。

从图4中可看出，在达到振动幅值的时间有些许误差，这主要是求解响应的积分方法导致的，精细积分方法在求解长时长的积分中具有较高的计算效率和具有较高的计算精度，本文主要是用区间方法来研究支承特性不确定下的磁悬浮系统的动态特性，因此不考虑高效率和高精度等算法问题，从图中可看出响应幅值的上下界和文献[20]的计算结果基本一致，从而可知本文所使用求解响应区间方法是合理和有效的。

(a) 文献[20]的仿真结果 (b) 本文计算结果

3 磁悬浮双转子系统的响应特性分析

针对图2所示的模型，本节将分别从支承特性不确定性下的磁悬浮双转子系统加速启动过程中瞬态响应和定转速下的稳态响应的展开分析，其中磁悬浮双转子系统确定性的物理参数为:PMB的刚度为1×107N/m，阻尼为1×104N·s/m，轴单元的弹性模量E= 2.1 ×1011Pa，泊松比μ= 0.269，密度ρ= 7850 kg/m3。

3.1 瞬态特性分析

3.1.1 变刚度下的磁悬浮双转子系统的瞬态响应

从图5可看出，转子系统的响应出现了两个振动峰值，其中低频峰值对AMB的等效支承刚度变化较为敏感，随着等效支承刚度的增加，低频峰值位置会向高频方向移动。同时，从图中还可看出，当支承特性不确定性时，双转子系统的动态响应在低频峰值附近受支承特性的影响程度较大，且动态响应的区间范围随等效支承刚度区间中值的增加而增大，而在高频附近，支承特性的不确定性对系统动态响应的影响十分有限。

从图6中可看出，在刚度区间1×105～1×106N/m低阶频峰值附近响应的不确定程度大致在10%左右，而在刚度区间1×106～1×107N/m低频峰值附近响应的不确定程度会大幅度增长，最大达到40%左右，可见在该刚度区间内，低频峰值附近响应受支承特性不确定的影响程度较大。在刚度区间1×105～1×107N/m内，低频附近响应的不确定程度与刚度近似呈现幂函数的关系,拟合出来的关系式为:

(19)

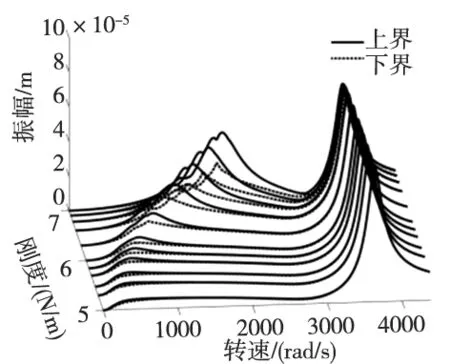
图5 圆盘1的瞬态响应

图6 低频峰值响应的不确定度与刚度的关系

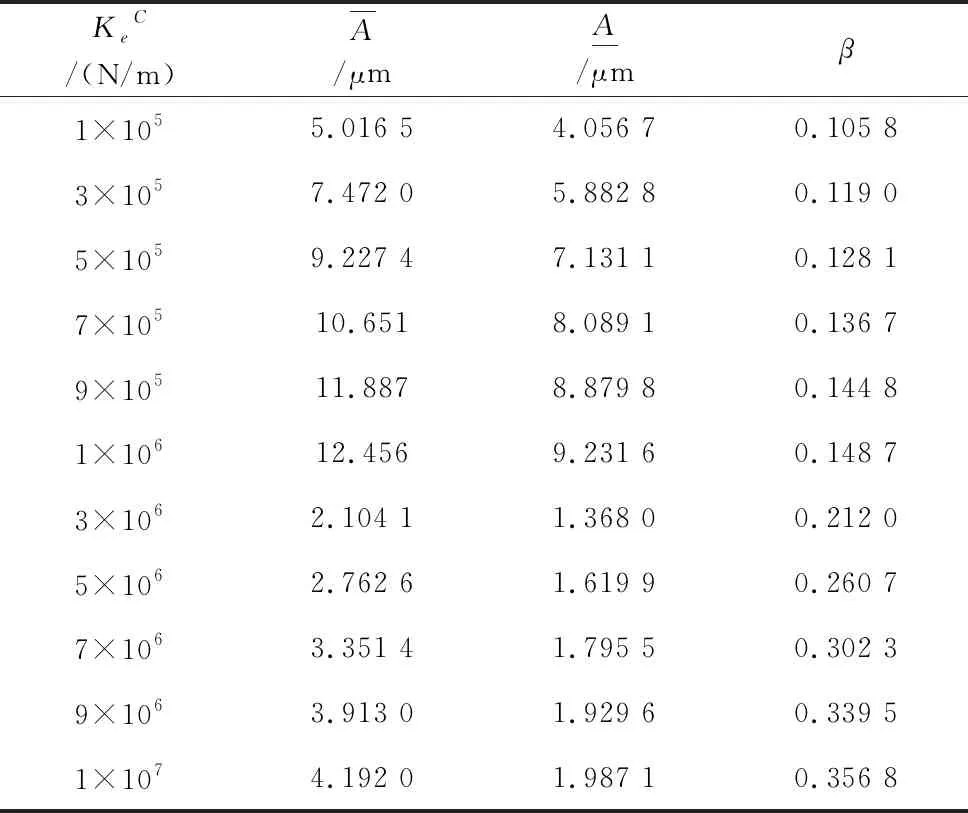
表1 低频峰值动态响应区间

3.1.2 变阻尼下的磁悬浮双转子系统的瞬态响应

(a) 刚度区间中值为5×105 N/m (b)刚度区间中值为5×106 N/m

从图7中可知，当等效支承阻尼的区间中值位于500～8000 N·s/m时，阻尼的变化虽然不会改变峰值的位置，但是当阻尼增大时能够很好的抑制低频振动峰值，同时，通过三幅图对比可知，当支承特性不确定时，低频动态响应的区间范围都随着等效支承阻尼的区间中值的增大而减小。

通过3.1节不确定度β定义的方式，分别计算出图7中各低频峰值响应的不确定度，得出这三个等效支承刚度区间中值下低频峰值响应的不确定度随阻尼的关系如图8所示。

从图8中可以看出，在不同等效支承刚度区间中值下，低频峰值动态响应范围的不确定度都会随着阻尼的增大而减小，并且不确定度最终都将趋近于10%左右。同时通过拟合可知，低频峰值动态响应范围的不确定度与阻尼也近似呈现幂函数变化的关系。

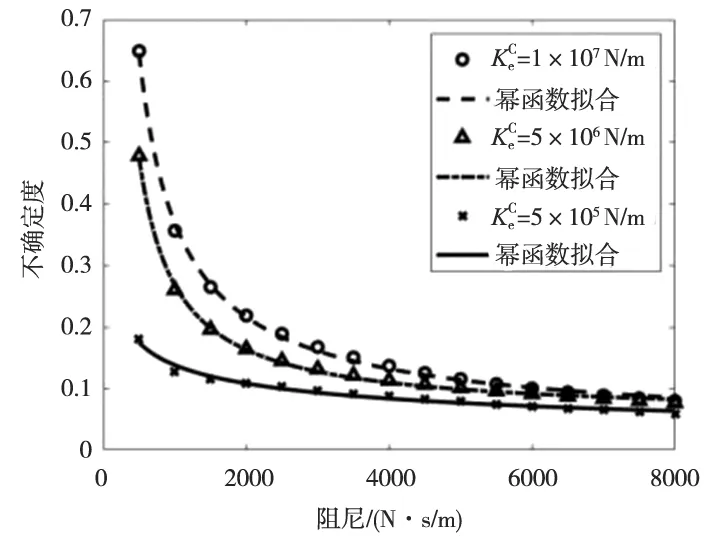
图8 低频峰值响应的不确定度与阻尼的关系

3.2 稳态特性分析

3.2.1 不平衡量位于内转子圆盘上时的稳态响应

当不平衡量仅位于内转子圆盘上时，取不平衡量大小fu= 1×10-5kg·m，转速比rΩ为1.2，以接近低阶振动峰值500 rad/s和远离低阶振动峰值1000 rad/s为例展开分析，内转子圆盘1的稳态时域响应和相对应的轴心轨迹分别如图9a、图9b所示。为了研究不同转速比下的影响规律，同时计算当转速比rΩ为1.5时，对应角速度分别为500 rad/s和1000 rad/s下内转子圆盘1的稳态时域响应和相对应的轴心轨迹如图9c图9d所示。

(a) 转速为500 rad/s，转速比为1.2 (b) 转速为1000 rad/s，转速比为1.2

从图9中可知，当不平衡量仅位于内转子上时，此时只存在内转子转频，图中轴心轨迹仅表现为单一的椭圆状，且支承特性不确定的转子都表现为正向涡动。同转速比不同转速下，转速在低阶临界转速附近时比越过低阶临界转速后所导致的支承特性不确定的磁悬浮双转子系统时域响应和轴心轨迹的范围要大，这也进一步验证了前面分析的正确性。同转速不同转速比下，由于AMB支承特性的不确定性是相同的且只存在内转子转频，故而转子系统的时域响应以及轴心轨迹不会因为转速比的变化而发生较大变化且时域响应和轴心轨迹的不确定性大致是相同的。

3.2.2 不平衡量位于内外转子圆盘上的稳态响应

当不平衡量同时位于内转子圆盘1和外转子圆盘3上时，不平衡量大小都取为fu= 1×10-5kg·m，转速比rΩ为1.2，同样以接近低阶振动峰值500 rad/s和远离低阶振动峰值1000 rad/s为例展开分析，磁悬浮双转子内转子圆盘1的稳态时域响应和相对应的轴心轨迹分别如图10a和图10b所示，以及当转速比为1.5时，内转子圆盘1的稳态时域响应和相对应的轴心轨迹如图10c和图10d所示。

(a) 转速为500 rad/s，转速比为1.2 (b) 转速为1000 rad/s，转速比为1.2

从图10中可知，当不平衡量同时位于内外转子上时，此时同时存在内转子转频和外转子转频，图中轴心轨迹均表现为内外交织的环形，且支承特性不确定的转子都表现为正向涡动。同转速比不同转速下，转速在低阶临界转速附近时导致支承特性不确定的磁悬浮双转子系统的时域响应以及轴心轨迹的范围也比转速越过低阶临界转速后所导致的时域响应和轴心轨迹的范围要大，由于不同转速引起内外转子的转频不同，故而导致内转子的时域响应和轴心轨迹前后表现出较大的差异。同转速不同转速比下，由于内转子转频相同而外转子转频不同，而导致内转子叠加后的时域响应和轴心轨迹前后有所不同，但是同一时间点下，某位置坐标下的时域响应的范围和轴心轨迹的不确定性程度大致是相同的。

4 结论

本文通过有限元法建立了一种磁悬浮双转子系统的理论模型，然后基于Chebyshev正交多项式的区间分析方法，分析了电磁轴承支承特性不确定的情况下，磁悬浮双转子系统瞬态特性和稳态特性，通过案例分析并对比仿真结果可以得出如下结论：

(1) 当支承特性不确定因子为10%时，在刚度区间为1×105～1×106N/m，低频峰值响应的不确定程度基本稳定在10%左右，在刚度区间为1×106～1×107N/m，会增长到40%左右。且在刚度1×105～1×107N/m范围内，低频峰值附近动态响应区间范围的不确定程度与刚度的变化近似呈现幂函数的关系。

(2) 阻尼增大能很好的抑制低频振动峰值，同时也能降低支承特性不确定所带来的低频附近响应的不确定程度。当支承特性不确定因子为10%时，随着阻尼的增大，低频峰值附近响应的不确定程度最将趋近于10%。

(3) 通过对支承特性不确定下磁悬浮双转子系统的稳态分析可知，同转速比下，转速的变化会影响支承特性不确定下的磁悬浮双转子系统的稳态时域响应和轴心轨迹的范围大小；同转速下，转速比对支承特性不确定下的磁悬浮双转子系统的稳态时域响应和轴心轨迹的影响会因为不平衡量的位置而表现出差异。