无转换参数下参考框架间Helmert直转模型及精度分析

姜英明，纪晓雨，侯晓伟，冯彦同

(1.千寻位置网络有限公司，上海 200438；2.潍坊职业学院农林科技学院，山东潍坊 262737)

0 引言

坐标参考框架是坐标系统的具体实现，通常通过一组核心站点的测站坐标和速度表示.坐标参考框架是测绘活动的参考基准[1]，同时，高精度的坐标参考框架也是进行空间大地测量学研究所必须的前提[2].各个坐标参考框架之间往往通过Helmert转换参数来联系.随着我国北斗卫星导航系统（BDS）的建成和BDS坐标系的启用，使用BDS进行精密定位定轨等研究和生产，都需要关注坐标框架的概念[3].为了准确使用各种参考框架，需要分析其转换的性质.

对于瞬时坐标系或精度要求不高的坐标转换，一般采用Helmert七参数进行.而对于高精度的坐标参考框架如国际地球参考框架(ITRF)，固定的Helmert七参数不能描述其框架的时变特性，因此Helmert七参数被视为是时变的，此时Helmert七参数被扩展成为Helmert十四参数[4].坐标参考框架在建立时，一般都会公布其到其他主流参考框架如ITRF之间的转换参数，以方便用户使用.

但在实际使用时，某些参考框架之间可能没有直接的转换参数，尤其对于某些区域性的坐标参考框架，此情形并不罕见.此时可通过某些“中间框架”如ITRF进行过渡，即首先将坐标或速度转换到具有直接转换参数的某个ITRF框架，再通过ITRF到目标框架的转换参数，将坐标或速度转换到目标框架.这造成了实际应用的复杂和不便.基于此类问题，本文推导了由间接的过渡参数计算直接转换参数的公式，以简化转换过程，提高计算效率.

1 坐标框架转换原理

1.1 Helm ert七参数情形

在不考虑框架转换参数变率的情况下，一般采用Helmert七参数进行坐标转换.假设从框架1到框架3之间没有直接的转换参数，但可以使用框架2进行过渡.记框架1到框架2的转换参数为T1、D1、R1；框架2到框架3的转换参数为T2、D2、R2.一般情况下，平移参数T的单位为mm，尺度缩放参数D的单位为10−9（ppb），旋转矩阵R的单位为千分之一秒（mas）.若坐标或角度分别以m或rad为单位，则T、D、R的量级分别为10−3、10−9、10−9.

依据布尔莎模型，将框架1下的某点P的坐标X1先转换到框架2再转换到框架3下的计算公式[5]为：

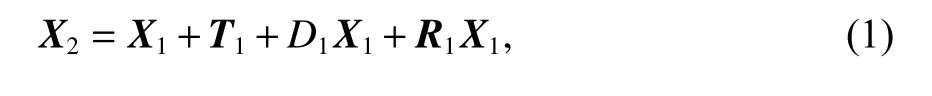
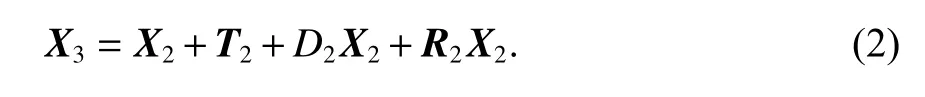
式中：X2为点P在框架2下的坐标；X3为点P在框架3下的坐标.将式(1)代入式(2)，可得

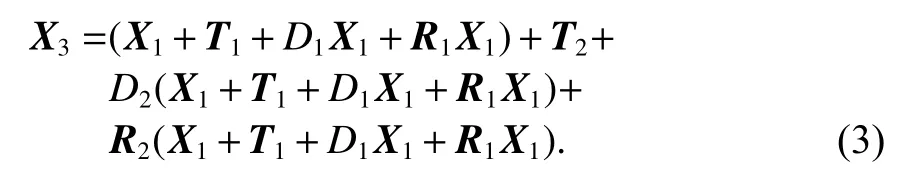
整理式(3)，可得式(4)：

式(4)中，D2(T1+D1X1+R1X1)和R2(T1+D1X1+R1X1)两项的量级皆为10−12m，在目前的测量精度下都可以忽略，因此在实际计算中，式(4)可以简化为

对比布尔莎模型的转换公式，可知框架1到框架3的直接转换参数T3、D3、R3可用式(6)计算：

1.2 Helmert十四参数情形

ITRF给出的各ITRF参考框架之间的转换参数也是时变的，因此其转换参数一般有14个，包括给定历元t0下的七参数以及其各自的变化率分别为：T、D、R、T˙、D˙、R˙.变化率的单位分别为mm/a、ppb/a和mas/a，其数量级分别为：10−3、10−9、10−9、10−3、10−9、10−9.

整理式(11)，可得

后两项的量级皆为10−12m/a，在计算时可忽略不计，因此速度的转换公式(12)可简化写为

同理，将式(7)、(8)代入式(9)，可得坐标的转换公式：

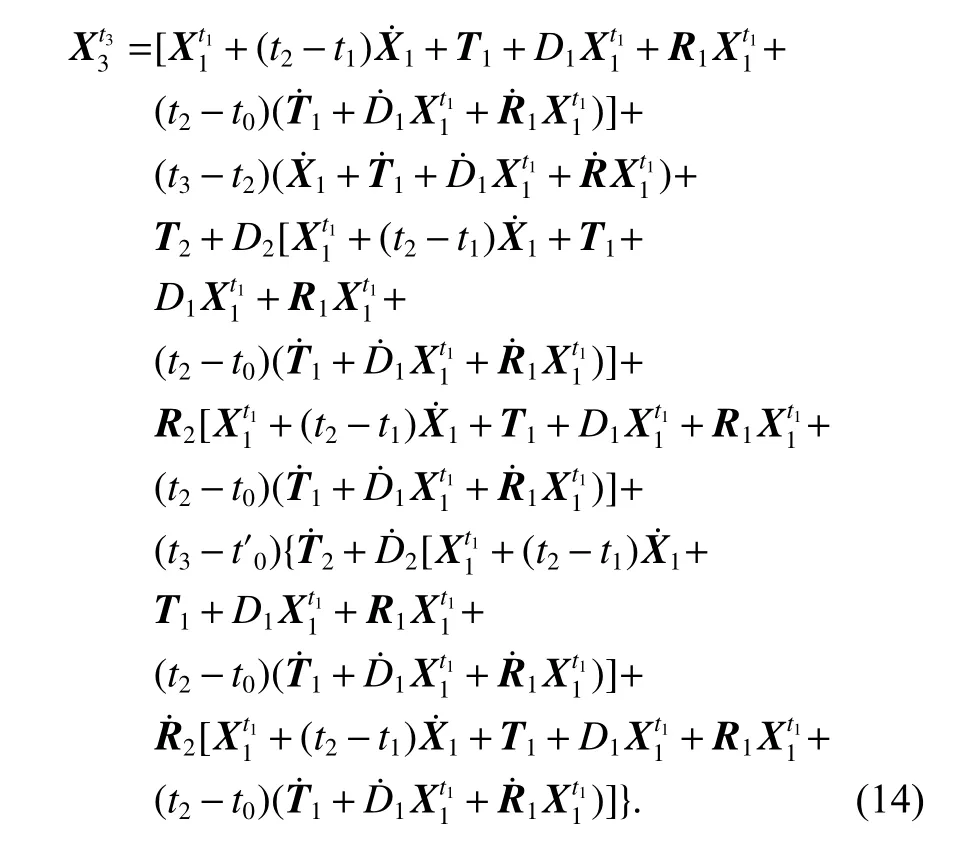
整理式（14）并忽略微小量，可得

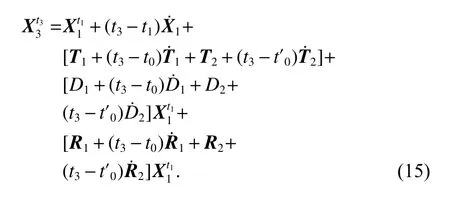
作为对照，式(7)亦可写成

2 算例验证

2.1 数据准备

欧洲参考框架网络（EUREF）由多个持续观测的永久性全球卫生导航系统（GNSS）站点构成，用于欧洲地区的参考框架维持.EUREF的数据由法国国家地理学院（IGN）或德国波兹坦地学中心（GFZ）统一处理，并基于其坐标和速度实现ETRS89坐标系.ETRS89是一种地心地固坐标系，其坐标系实现包括ETRF2000、ETRF2005和ETRF2014等[6].EUREF的站点分布由图1所示。

图1 EUREF站点分布图

EUREF公布了其 714个站点分别位于ITRF2014、ETRF2014和ETRF2000框架下的坐标和速度，同时公布了ETRF到各ITRF框架的转换参数.但是，其公布的成果中并未包含ETRF2014到ETRF2000的转换参数.本文以将EUREF站点坐标从ETRF2014转换到ETRF2000为例，验证由式(17)计算直接转换参数的可行性.此时坐标转换有两种方案：

1）首先将坐标和速度从ETRF2014转到ITRF2014，然后再从ITRF2014转换到ETRF2000，记为方法A；

2）使用式(17)计算ETRF2014到ETRF2000的直接转换参数，然后对ETRF2014框架下的坐标和速度进行转换，记为方法B.

EUREF公布的2010.0历元下，ETRF2014转换到ITRF2014的转换参数如表1所示：

2010.0历元下，ITRF2014到ETRF2000的转换参数如表2所示：

表1 ETRF2014到ITRF2014的转换参数

表2 ITRF2014到ETRF2000的转换参数

由式(17)计算得，方法B所使用的2 010.0历元下ETRF2014到ETRF2000的直接转换参数如表3所示：

表3 ETRF2014到ETRF2000的转换参数

2.2 结果分析

作为验证，首先使用方法A将714个站点在ETRF2014下的坐标和速度转换到ETRF2000，并将转换成果与EUREF官方公布的数据进行对比.统计方法A与EUREF官方公布的ETRF2000框架下坐标和速度的差异，统计结果如表4所示：

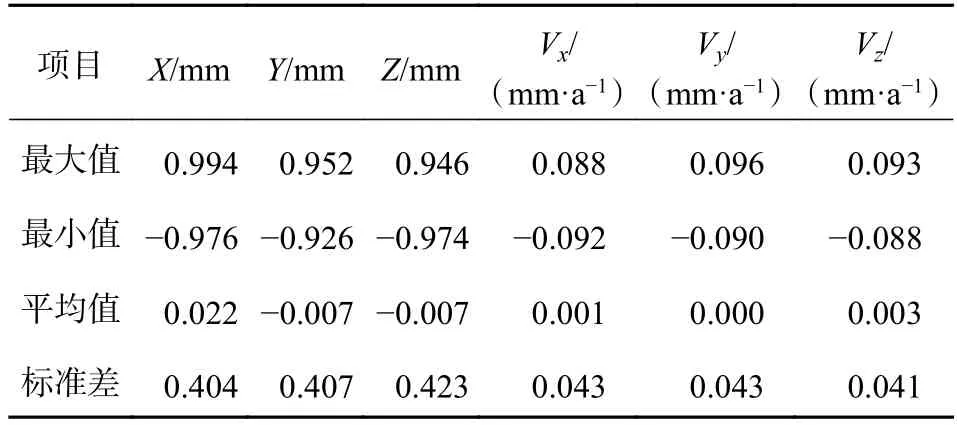
表4 方法A计算结果与官方数据对比统计

其坐标和速度的差异分布分别如图2、图3所示：

图2 方法A与ETRF2000公布的坐标的差异分布

图3 方法A与ETRF2000公布的速度的差异分布

从统计可以看出，方法A与EUREF官方公布的站点在ETRF2000框架下的成果，坐标差异均优于1mm，速度差异均优于0.1mm/a，且差异有正有负均匀地分布在0两侧，这说明方法A所进行的转换是正确的，其转换差异主要受到偶然误差的影响.

然后通过方法B使用表3中的转换参数进行坐标转换，并将其转换成果与方法A作为对比.差异分布统计如表5所示：

差异分布如图4、图5所示：

表5 方法A与方法B计算结果对比统计

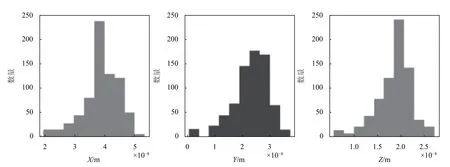
图4 方法A与方法B坐标差异分布图

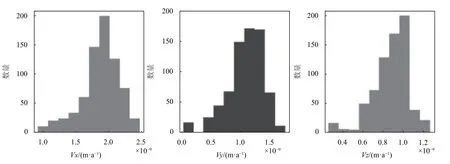
图5 方法A与方法B速度差异分布图

由以上统计可以看出，基于方法A和方法B得到的坐标差异均为10−8m量级，速度差异为10−9m/a量级.并且，其差异均大于0，说明二者之间存在系统差.结合方法B的推导过程，易知这是因为方法B的计算过程中忽略了一些微小量所造成的.但由于二者差异足够小，因此可认为方法A和方法B在一般使用中是等价的.

为验证式（18），使用参考框架ETRF2014到ITRF2014的转换参数，将ETRF2014下的基站速度转换到ITRF2014.作为对比：

1）方法C使用站点在ETRF2014下的坐标；

2）方法D假定站点在ETRF2014下的坐标未知，使用其在ITRF2014下的坐标近似.

两种方法的差异统计如表6所示。

表6 使用精确和近似坐标进行速度转换对比

其差异分布如图6所示。

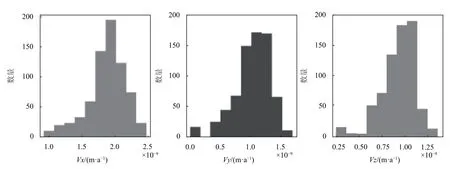
图6 使用精确坐标与概略坐标转换速度的差异分布图

由以上统计可发现，由方法C和方法D所计算的基站速度差异在10−9m/a量级.二者虽然存在一定的系统差，但在实际使用时完全可以忽略.

3 结论

利用Helmert转换公式进行坐标转换时，对于没有直接转换参数的坐标框架，使用多步“过渡”的方式进行转换时公式复杂低效.本文对传统的间接坐标转换方法进行改进，推导了坐标框架间的直接转换公式，并使用714个EUREF站点在ETRF2014和ETRF2000的坐标和速度进行验证，得出以下结论：

1）对于Helmert七参数坐标转换，两个框架的直接转换参数可由作为过渡的框架转换参数求和计算，计算方法如式(6)；

2）对于Helmert十四参数坐标转换，两个框架的直接转换参数，其Helmert七参数的变率可由作为过渡的框架转换参数的变率求和计算，Helmert七参数可将作为过渡的转换参数归算到某一相同历元后求和计算，计算方法如式(17)；

3）在对速度进行框架转换时，若与原框架下速度对应的坐标未知，可使用其他框架下相差不大的坐标代替.

总体而言，坐标转换的直接参数法和间接参数法差异较小，但本文的转换方法可简化计算步骤，各参考框架之间的转换参数可提前计算后保存，方便程序实现，也可以节约计算资源.