窄带与脉冲干扰对卫星导航信号载噪比的影响
2021-03-26郭海玉鲁祖坤陈飞强刘小汇庄钊文
郭海玉,鲁祖坤,陈飞强,刘小汇,庄钊文
(国防科技大学导航与时空技术工程研究中心,长沙 410073)
0 引言
卫星导航信号从卫星传播到地面,距离长、损耗多,因此,接收机接收到的信号十分微弱,是被淹没在噪声中的,而且极易掺杂干扰信号.导航接收机受到来自外部或内部的干扰主要包含欺骗干扰和压制干扰两种.本文只研究压制干扰对载噪比的影响.压制干扰的原理比较简单,主要采取将一定频率的大功率信号送入接收机的方式,使接收机内信号载噪比降低以至无法正确捕获和跟踪卫星导航信号,严重影响接收机正常运作.压制干扰进入接收机的功率大小通常用干信比或干噪比来评估,一个接收机可容忍的干噪比或干信比是有一定范围的.除干扰功率外,干扰的样式、干扰的持续时间、干扰频率与信号频率的关系等,也都会影响接收机内载噪比的变化.全球卫星导航系统(GNSS)接收信号的载噪比一般在35 ∼55 dB·Hz,大于40 dB·Hz的一般是强信号,小于28 dB·Hz的视为弱信号[1].卫星导航信号经过射频前端和相关器信号处理后,输出的载噪比的大小会直接影响信号捕获跟踪的性能,也会影响整个接收机的定位解算性能.因此,研究不同干扰的性能对于接收机采取合理的抗干扰措施和提升接收机性能有很大意义.
最为常见的压制干扰样式主要有单音干扰、宽带干扰、扫频干扰、窄带干扰和脉冲干扰,它们的干扰模型和功率谱对于研究其干扰性能具有很大作用.有些形式的信号可以直接利用经验值代入,例如宽带高斯白噪声的经验Q值为2.22,匹配谱干扰的经验Q值为1.5,谱峰处的单频干扰经验Q值为1[1].但是窄带干扰和脉冲干扰由于自身的中心频率和带宽等参数不确定、不唯一的特点,并不能直接给出经验值.而且,国内外关于脉冲干扰性能评估的一般方法误差较大,也没有明确其抗干扰品质因数的公式.因此本文将对比窄带干扰抗干扰品质因数的计算方法,分析脉冲干扰的抗干扰品质因数的计算公式.
窄带干扰突出的特点是频域上集中,干扰的功率集中在较小的频段内,干扰频率在信号频谱主峰频段内的窄带干扰会对卫星导航信号造成极大的影响.目前,针对窄带干扰的性能评估方法基本完善,而且评估效果较好.文献[2]中指出,当窄带干扰带宽足够小时,可以将窄带干扰功率谱近似为冲激函数计算其抗干扰品质因数.文献[3]中认为窄带干扰的频宽是一个相对值,不能一味用冲激函数近似功率谱,提出带内平稳的窄带干扰的归一化功率谱可以用干扰带宽的倒数近似.与窄带干扰不同的是,脉冲干扰的突出特点是时域的周期性和不连续性,其参数主要包括干扰功率、干扰频率、占空比、脉冲周期等.目前,针对脉冲干扰性能的研究相对较少,文献[4]、文献[5]中用评估窄带干扰和单频干扰的方法计算脉冲干扰的抗干扰品质因数,并不能普遍适应所有的脉冲干扰情况.文献[6]中针对脉冲干扰性能分析做了大量研究,他提出频域上分析脉冲干扰下等效载噪比计算的五种情况,但是计算复杂度高,功率谱用离散的主瓣频谱近似,具有较大误差.文献[7]在时域上直接给出了脉冲干扰下阵列信号相关后等效载噪比的计算公式,但是分析得不彻底,而且没有给出合理的方法计算不同参数下脉冲干扰的抗干扰品质因数.为了更好地评估脉冲干扰的干扰性能,更加准确地计算脉冲干扰下信号的载噪比损耗,提出一种新的计算方法是十分有必要的,而且,准确的脉冲干扰性能评估对于日后分析更加复杂的干扰样式打下坚实的基础.
本文在总结一般等效载噪比的计算公式的基础上,提出了在时域上计算脉冲干扰的相关后载噪比的计算方法,并给出了脉冲干扰抗干扰品质因数的计算公式.本文第一节讲述干扰条件下卫星导航信号载噪比的评估方法;第二节描绘了不同干扰场景对品质因数的影响分析,着重分析了脉冲干扰占空比和干扰时间对抗干扰品质因数的影响;第三节对提出的抗干扰品质因数公式和不同干扰下等效载噪比数值做了仿真验证;最后,第四节陈述本文结论.
1 干扰条件下卫星导航信号载噪比的评估方法
载噪比是衡量卫星导航信号质量的重要指标,对于接收机的信号处理具有重要的意义,载噪比[8]的定义如下:

式中:Ps为接收机接收到的信号功率;N0=10 lg(kT0)表示热噪声功率.当没有受到外界干扰时,考虑接收机的增益和电路损耗,以dB为单位表示的载噪比为

式中:k=1.38×10−23(J/K)为玻尔兹曼常数;Nf表示温度为290 K时放大器噪声系数;L表示接收机损耗.
当接收机受到干扰时,信号的载噪比会降低到等效载噪比(C/N0)eq,其计算公式为
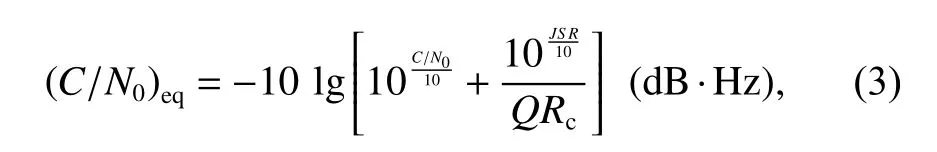
式中:C/N0(dB)为没有干扰时信号的载噪比,可通过式(1)或式(2)计算得到;Rc为码率;Q为抗干扰品质因数;JS R=Cj/Cs(dB)表示干信比.由式(3)进而可得出干扰条件下信号载噪比损耗为

由式(3)和式(4)可得,当接收机受到干扰时,信号的载噪比及其损耗是干信比和抗干扰品质因数的函数,抗干扰品质因数越大,等效载噪比越高,载噪比损耗越小.
在干扰条件下要计算信号的载噪比或载噪比损耗,首先要计算信号的品质因数,抗干扰品质因数与信号调制方式和干扰类型有关,高斯带限干扰模型下抗干扰品质因数[9]的计算公式为

式中:Gs(f)为信号经过射频前端滤波器后的功率谱密度;Gj(f)为干扰的归一化功率谱密度函数.由式(5)可知,抗干扰品质因数既受信号功率谱密度的影响,也依赖于干扰波形、中心频率和干扰带宽等参数[10-11].
2 不同干扰场景对相关后载噪比的影响分析
2.1 窄带干扰
假设信号采取二进制相移键控(BPSK)调制方式,由于窄带干扰信号具有一定带宽,Gs(f)可以采用无周期码信号的功率谱密度函数(信号连续功率谱密度函数)等效[12],公式如下:
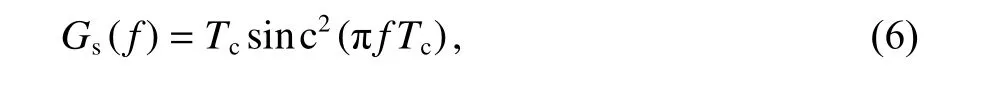
式中:Tc表示码元宽度,Tc=1/Rc.若窄带干扰功率谱平坦,中心频率为Fj,带宽为Bj,其功率谱可等效为
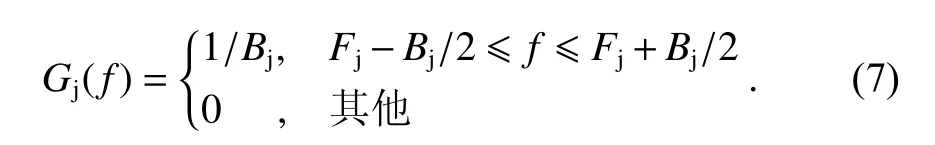
将式(6)和式(7)代入式(5)可得窄带干扰的抗干扰品质因数为
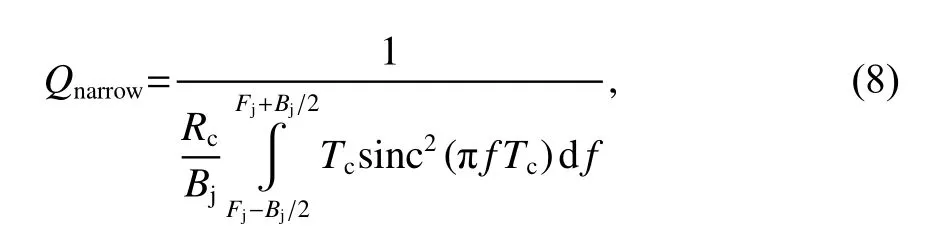
将计算出的Q值代入式(3),可得窄带干扰下信号的等效载噪比为

2.2 脉冲干扰
脉冲干扰相比于窄带干扰在时域和频域上有很大不同,脉冲干扰时域上不连续性周期性特点突出,而在频域上很难表示出一致的或等效的功率谱密度,所以,不能用上述求解窄带干扰抗干扰品质因数的方法直接带入,下面分析脉冲干扰下信号等效载噪比的计算和抗干扰品质因数的表达公式.
计算脉冲干扰的抗干扰品质因数,首先要计算脉冲干扰下信号的相关后载噪比,也就是要计算信号经过相关器处理后的脉冲干扰功率、噪声功率和卫星导航信号功率.经典方法是在频域内计算的,本文从时域上推导脉冲干扰下信号相关后的等效载噪比.
接收机的相关器的处理过程主要分为三步:载波剥离、伪码剥离和相干积分.其工作流程如图1所示.

图1 相关器结构示意图
接收机接收到的信号经射频前端处理后可表示为[13]

式中:s[n]为中频载波调制的卫星导航信号;j[n]为干扰信号;w[n]表示白噪声.经过相关器处理后,信号可以表示为

式中:r[n]为相关器输出总的信号;Tcoh为相干积分时间;s0(t)为接收机本地产生的伪码;f0为复制载波频率;τc为码时延,本文中假设码时延为0;rss[n]、rsj[n]、rw[n]分别为卫星导航信号、脉冲干扰和噪声经载波剥离和伪码剥离后的信号.以脉冲为例具体推导过程如下:
脉冲干扰的信号模型为

式中:p(t)为占空比,为τj/Tj的矩形脉冲干扰;fJ为干扰频率;Aj为脉冲干扰信号幅度.

I/Q混频中,被分为两个支路的脉冲干扰信号分别与正弦复制载波uos(t)和余弦复制载波uoc(t)相乘,经积化和差化简并滤掉高频成分得:

式中:Aj表示信号幅度;wg和θg分别为输入信号和复制信号载波频率差异和初相位差异.
相关器又称为匹配滤波器,可以通过接收信号与本地伪码相乘将信号中的伪码剥离:

式中,Rsj(τ)代表输入信号与本地PRN码的相关函数,与干扰的参数有关,其表达式为
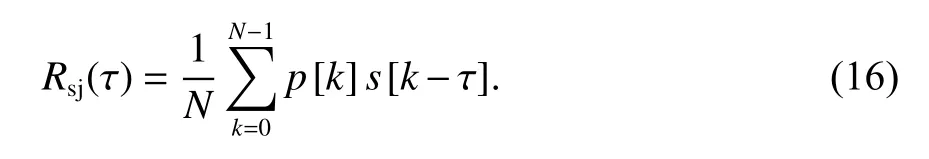
式中,N为参与相关运算的离散数据点数目,它通常对应相关时间Ta=1ms长的采样数据量,通常可以忽略,对载噪比的计算无影响.
一般情况下,可假设码时延τ=0,频域上Rsj(0)的求解方法是将p[k]和s[k]做傅里叶变换[14],取近似且仅保留主瓣频谱得:

将(17)和(18)代入(16)得

式中:Ni、Ns分别表示脉冲和伪码主瓣谱线编号;vm、ul表示各谱线系数.
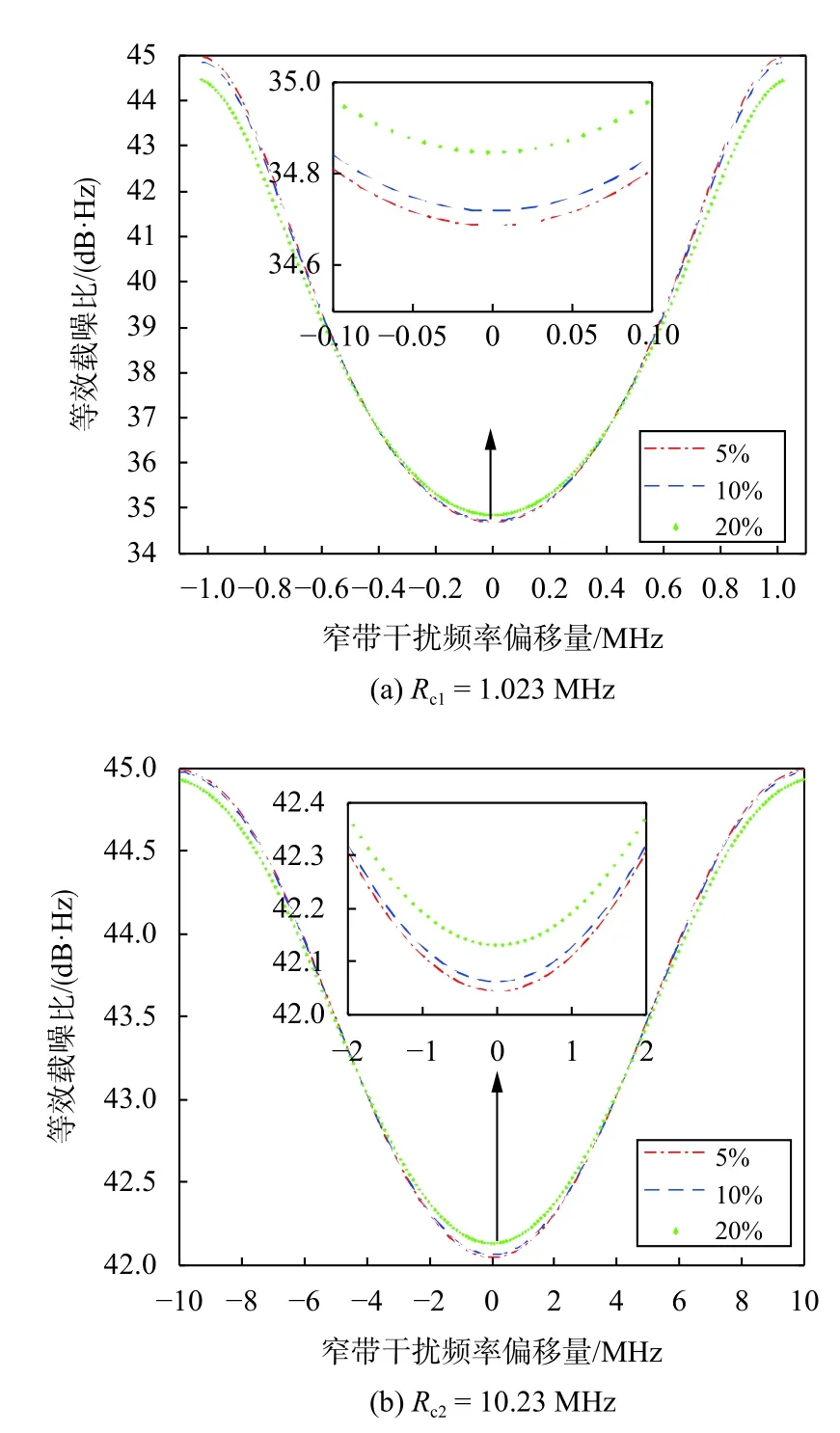
本文从时域上进行计算脉冲干扰相关结果更准确,由于相关时间Ta一般为1ms[15],接收机受到脉冲干扰的周期数Nj和脉冲干扰周期Ti是不确定的,而且相干积分可认为是相关结果的累加[16-18],假设脉冲干扰周期固定且小于相关时间,所以考虑脉冲干扰持续时间、相关时间和相干积分时间的关系,可分NjTj 以脉冲干扰时间小于相关时间为例进行具体分析,即NjTj 式中:wg=2πfg,fg=fJ−f0表示干扰频率与复制载波频率之差.将上述相关积分结果合在一起,并以数字信号表示,可以写成如下的复数形式: 式中:Pj0表示预检前脉冲干扰功率;Rss(τ)表示最大值为1的输入伪码与复制信号的相关结果.假设信号中频与复制载波频率一致,码时延τ=0,那么预检前和相干积分后信号功率和噪声功率密度不变,则等效载噪比可表示为 其余两种情况可类比于NjTj 结合式(3)和式(25),脉冲干扰的抗干扰品质因数可记为 由式(26)可以看出,脉冲干扰的抗干扰品质因数既与相干积分时间有关,也与脉冲干扰占空比、持续时间和干扰周期有关. 选用200 ms长度的信号数据,采样率Fs=25 MHz,窄带干扰带宽分别为5%、10%和20%的伪码中心频宽,窄带干扰中心频率在伪码中心频宽内以0.01MHz遍历,以下简记为频率偏移量.调制方式分别选取BPSK(1)和BPSK(10),即Rc1=1.023MHz和Rc2=10.23MHz.设定载波中频与复制载波频率相同,干信比为JS R=25 dB. 如图2(a)所示,信号调制方式为BPSK(1),干信比设置为25 dB,卫星导航信号的载噪比损耗最大约为10 dB;如图2(b)所示,信号调制方式为BPSK(10),干信比设置为25 dB,信号的载噪比损耗最大约为3 dB,BPSK(10)调制方式抗干扰能力较强.除此之外,等效载噪比曲线形状是基本一致的.由上述数值分析,可得以下结论:窄带干扰频偏越小,抗干扰品质因数越小,等效载噪比越小.在该参数设置下,窄带干扰中心频率偏移量在0附近时,可以明显看出,20%伪码带宽的窄带干扰引起的载噪比损耗相比于5%和10%伪码带宽的情况要小,其抗干扰品质因数较大. 图2 窄带干扰带宽和频偏对等效载噪比的影响 3.2.1 脉冲干扰持续时间与抗干扰品质因数 脉冲干扰抗干扰品质因数理论计算的各参数设置如下:设定脉冲干扰频率与信号中频以及复制载波频率相同,脉冲干扰的占空比分别为10%、15%和20%,脉冲干扰周期Tj=100 us,相关时间Ta=1 ms,为分别体现脉冲干扰时间与相关时间和相干积分时间的关系,如图3所示,本文设置相干积分时间Tcoh=20 ms,脉冲干扰周期数从1~300遍历. 图3 脉冲干扰时间与其抗干扰品质因数的关系 由图3可知,脉冲干扰的抗干扰品质因数是随干扰时间变化的,干扰时间越长,抗干扰品质因数越小.当脉冲干扰时间太短或占空比较小时,信号受到的干扰较小,所以抗干扰品质因数较大.当脉冲持续时间大于相干积分时间,占空比固定时,抗干扰品质因数为常数.占空比越大,抗干扰品质因数越小. 3.2.2 干扰中心频率和占空比的变化对等效载噪比的影响 为验证上述理论结果的准确性,用上述抗干扰品质因数计算脉冲干扰下信号等效载噪比,并与接收机实测仿真结果对比.三种情况下等效载噪比区别是干扰功率乘的系数不同,故本文以其中一种情况为例对脉冲干扰下等效载噪比仿真,假定脉冲干扰持续时间足够长,即Tcoh⩽NjTj.其他参数值设置如下:Rc1=1.023MHz和Rc2=10.23MHz,Ta=1ms,Tcoh=1ms;初始载噪比C/N0=45 dB·Hz,干信比JS R=54 dB,其中信号功率Ps=−160 dBW,噪声功率密度N0=−205 dB·Hz;干扰功率Pj0=−106 d BW,干扰频偏以50 Hz遍历;仿真信号长度为200ms. 图4 不同脉冲干扰下卫星导航信号等效载噪比变化图 由图4分析可得,干信比设置为54 dB,调制方式分别为BPSK(1)和BPSK(10)时等效载噪比损耗不同,曲线形状大致相同,脉冲干扰的干扰效能要低于相同干扰强度的窄带干扰.当脉冲干扰频率与信号频率相同时,等效载噪比最小,当干扰频率偏移大于一定值时,对等效载噪比几乎没有影响.占空比越大,等效载噪比越小,抗干扰品质因数也越小. 为便于对比,选取仿真结果与计算结果的极小值点作比较,即最大误差点,得如下表格: 表1 等效载噪比理论结果与仿真结果对比表 从理论结果和仿真结果来看,不同条件下最大误差均优于0.5 dB,仿真效果较好,由上述推导求出的脉冲干扰等效载噪比计算公式和脉冲干扰抗干扰品质因数的定义具有一定参考性. 本文分别从频域和时域的角度计算了窄带干扰和脉冲干扰的抗干扰品质因数以及两种干扰下信号的相关后载噪比,并进行分析和仿真验证.结果表明:抗干扰品质因数的大小会直接影响相关后载噪比的大小,其他条件不变的情况下,两者是正相关的;无论是窄带干扰还是脉冲干扰,干扰频偏越小,即干扰频率离信号频率越近,抗干扰品质因数越小,等效载噪比也越小;窄带干扰的抗干扰品质因数可以直接用经典方法从频域上求得,在一定频率偏移范围内,窄带干扰的带宽越大,抗干扰品质因数越大;脉冲干扰是与特征明显,其抗干扰品质因数是与脉冲干扰持续时间密切相关的,而且当脉冲干扰时间足够长时,抗干扰品质因数为一个常数,此外,脉冲干扰的抗干扰品质因数还受占空比的影响,占空比越大,其值越小.由本文可以看出,脉冲干扰的抗干扰品质因数计算公式是较为复杂的,难以给出特定的经验值,使用时应分情况计算;分析不同干扰类型的抗干扰品质因数,对于研究干扰的性能和采取抗干扰措施具有重要的参考价值. 致谢:感谢导航与时空技术工程研究中心老师团队的支持和帮助.

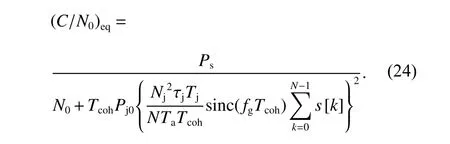

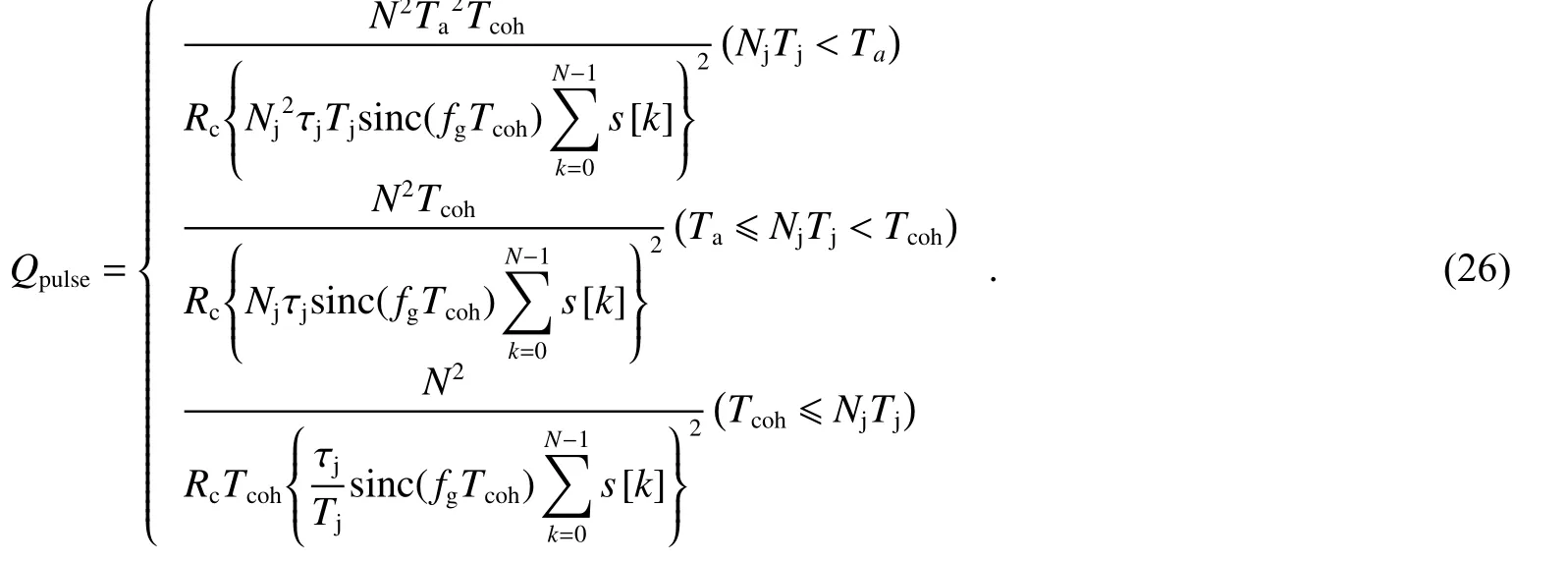
3 理论计算与仿真验证
3.1 窄带干扰下的相关后载噪比
3.2 脉冲干扰的抗干扰品质因数及卫星导航信号相关后载噪比



4 结束语
