复合材料MMB试件I-II混合型层间裂纹扩展分析
2021-03-26邓健卢天健尹乔之
邓健,卢天健,*,尹乔之
1. 南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016 2. 南京航空航天大学 多功能轻量化材料与结构工业和信息化部重点实验室,南京 210016 3. 南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016
飞机复合材料结构多为典型的薄壁层合板/夹芯结构,在外部载荷作用下易发生分层损伤。严重的分层损伤不仅会很大程度地影响整体结构刚度,还是导致结构最终失效破坏的关键因素[1-2],因此亟需发展有效、可靠的分层损伤预测方法,以最大限度提高复合材料结构设计能力。近年来,基于黏聚区模型(Cohesive Zone Model,CZM)的界面单元法被广泛用于模拟复合材料结构的层间失效[3-4]。然而,数值模拟中黏聚区长度与界面单元尺寸的确定、计算收敛性与数值稳定性等问题仍一定程度地阻碍了其在更复杂结构中的应用[5]。建立基于黏聚区模型的层间裂纹扩展分析模型,能够以较低成本讨论界面性能参数、本构形式以及外部载荷形式等对裂纹扩展和最终失效载荷的影响,有利于深刻揭示分层损伤萌生及裂纹扩展的力学机理[6]。尤其是针对典型层间断裂模式的裂纹扩展分析与评估,能够为有限元分析中的界面参数选择提供依据,同时为复合材料断裂韧性试验的设计和数据处理方法的发展提供理论基础。
针对具有单一断裂模式的典型双悬臂梁(DCB)和端部缺口弯曲(ENF)试件中的裂纹扩展,国内外均开展了广泛研究。Kanninen[7]首先建立了DCB裂纹扩展的简单梁模型,其假设开裂部分为弹性固定在裂纹尖端区域的欧拉-伯努利梁,并采用弹簧力模拟了裂纹界面的应力。Williams和Hadavinia[8]将该模型拓展到多角度铺层的DCB试件,讨论了不同黏聚区本构和材料参数对I型裂纹断裂韧性预测值的影响。Carlsson等[9]基于铁木辛柯梁理论分析了ENF试件的裂纹扩展,讨论了剪切变形对能量释放率的影响。Williams[10]考虑了裂尖变形和转角的影响,修正了裂纹长度计算方法,提高了II型裂纹扩展的准确性。通过引入黏聚区软化过程以考虑层间失效机理,Wang和Qiao[11]给出了更为合理的断裂韧性的求解方法。陈瑛和乔丕忠[12]将双线性黏聚区本构引入到4ENF试件中,研究了界面应力分布情况,但并未详细讨论裂纹扩展过程。刘伟先等[13-14]研究了单向复合材料DCB及ENF试件中的裂纹扩展,认为裂纹扩展之后黏聚区长度保持定值,但是,刘伟先等[14]的工作仅涉及了ENF试件的裂纹长度小于试件半长的情况,但未分析II型裂纹长度超过试件半长后的裂纹扩展过程。
在工程实际中,相较于单一型断裂模式,混合断裂模式更为常见,混合断裂模式下的裂纹扩展分析及能量释放率的计算也更加复杂[2-3]。Reeder和Crews[15]于1990年提出的混合模式弯曲(MMB)试件是目前应用广泛的混合断裂试件,通常用于测量混合模式下的临界能量释放率及表征混合模式的黏聚区本构[15-16]。基于线弹性力学假设和载荷分配,Reeder和Crews[15]将其等效为DCB与ENF试件的叠加,对于裂纹长度未超过试件半长的情况,获得了较好的预测结果。在Williams[10]裂纹长度修整方法的基础上,de Morais和Pereira[17]分析了多角度层合板的混合断裂。Blanco等[18]给出了MMB试件加载臂长与混合模式比的函数关系,Mi等[19]则给出了裂纹长度超过试件半长时的能量释放率计算公式,但未讨论不同模式混合比对预测结果的影响。Bennati等[20]进一步考虑了MMB试件中I型裂纹分量的微小刚体转动,以保证其与MMB及ENF分量的边界条件保持一致,但未考虑黏聚区软化行为对裂纹扩展的影响。
本文基于经典层合板理论及黏聚区模型,建立含一般分层裂纹层合板的理论模型,对I-II混合型断裂MMB试件进行裂纹扩展分析。该模型充分考虑了黏聚区的软化过程,采用合理的裂纹叠加模型,引入I型裂纹分量(DCB试件)的刚体转动位移,考虑中部载荷对裂纹扩展的闭合效应,分段获得了位移函数通解。结合叠加模型的边界条件与连续性条件,求解获得了载荷-位移曲线,将预测结果与试验及梁模型预测结果进行对比,以验证该理论模型的有效性。利用该理论模型,进一步研究了在裂纹扩展过程中断裂模式混合比、黏聚区长度的变化及闭合效应的影响。本文结果不仅为复杂结构的分层裂纹扩展分析提供理论依据,还为数值仿真提供一个可靠的交叉检验工具。
1 含一般分层裂纹的层合板模型
考虑含有一般分层裂纹的层合板,长为2L,宽为b,分层后的上下半板分别厚h1、h2,其几何尺寸及坐标系如图1所示。设贯穿该层合板宽度方向且与其长度方向平行的裂纹长度为a。同时假设该分层裂纹仅沿已有裂纹方向扩展,潜在裂纹在图1中以虚线标出。假定沿分层裂纹界面将层合板分为上下两半板,且其横截面表现为平面应变状态。本文所讨论的复合材料层合板多为薄壁结构,符合经典层合板理论的应用范围[21],则上下两半板在各自局部坐标系中的位移场可表示为
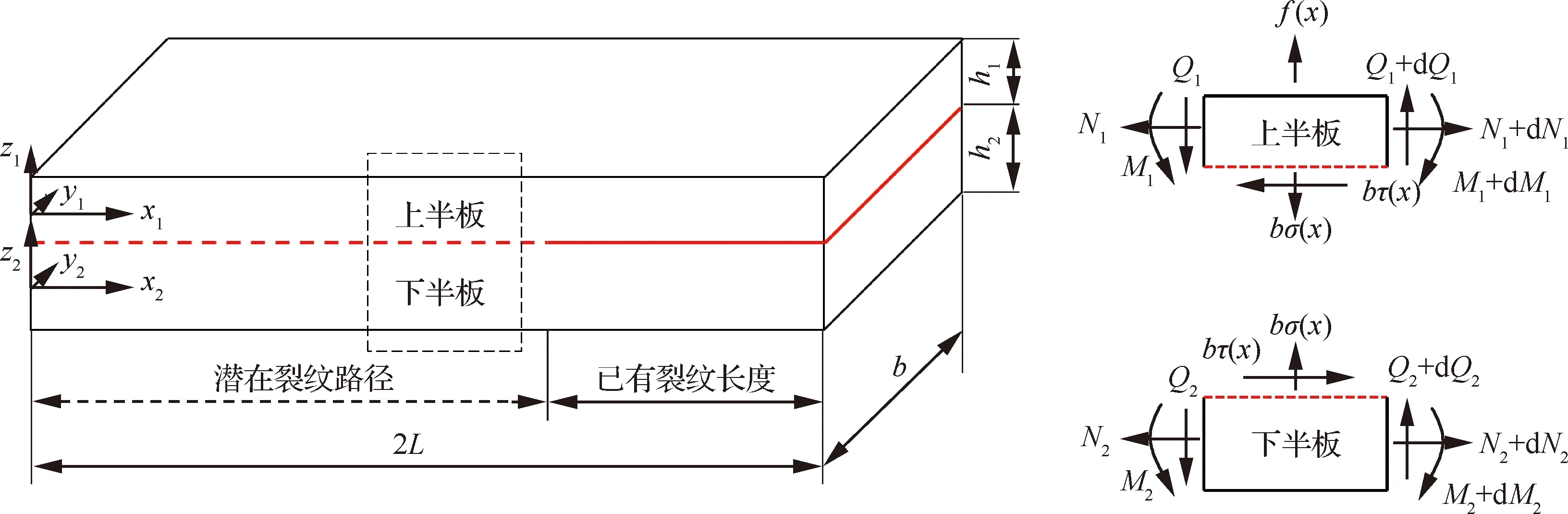
图1 含一般分层裂纹层合板微元段的受力分析Fig.1 Free body diagrams of sub-elements in general cracked laminates
(1)
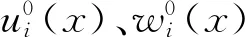
由于微元分析只考虑上下两半板在xOz平面内的变形[22],上下两半层合板中的本构关系可简化为
(2)
式中:A11i、B11i、D11i分别为拉伸刚度、耦合刚度及弯曲刚度;Ni为轴向力;Mi为弯矩。假设裂纹扩展过程中上下两半板处于小变形状态,根据上下两半板微元段的受力平衡条件,忽略高阶项,则含一般分层裂纹的复合材料层合板(上下两半板)的控制方程为
(3a)
(3b)
式中:Qi表示截面剪力,i=1,2;σ(x)、τ(x)分别为裂尖黏聚区的法向应力和切应力,可根据黏聚区本构关系(Traction-Seperation, T-S)确定;f(x)为面外分布载荷,由于本文讨论的DCB、ENF及MMB试件仅受到局部集中载荷,因此f(x)=0。为保持应力方向与相对位移方向一致,定义法向相对位移Δn为上半板相对下半板的张开位移,切向位移Δs为上半板相对下半板的滑开位移:
(4)
根据双线性黏聚区模型(图2),可将黏聚区应力τ与相对位移Δ的本构关系表示为
τ=
(5)
式中:Kinitial、Ksoften分别为线弹性及软化阶段的切线刚度,且Kinitial>0、Ksoften<0;Δonset为黏聚区损伤起始时的相对位移,Δultimate为最终有效相对位移,此时分层裂纹发生扩展;τc为界面应力强度。曲线包围面积为界面断裂韧性GC。
由此,含一般分层裂纹的层合板理论分析模型已基本建立,包括:由式(1)给出的变形协调条件,式(2)给出的层合板本构关系,式(3)给出的受力平衡关系,以及式(5)给出的黏聚区本构关系。联立以上微分方程,并结合具体层合板结构及加载工况所确定的边界条件和连续性条件,便可进行求解。针对本文中I-II混合型层间裂纹扩展的MMB试件(图3),其边界条件可表示为
(6)
特别地,在PII加载点处,引起了剪力突变,其突变的绝对值为载荷P的大小,即为
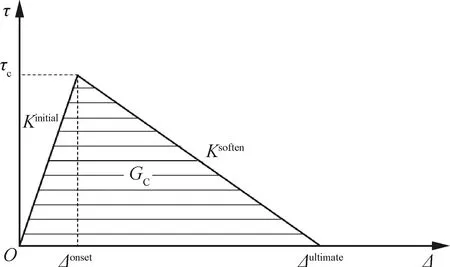
图2 双线性黏聚区本构模型Fig.2 Bilinear T-S law for cohesive zone

图3 MMB试件几何尺寸及加载情况Fig.3 Geometric dimensions and loading conditions of MMB specimen
PII+Q1(L-)=Q2(L+)
(7)
2 MMB试件裂纹扩展分析
如图3所示,MMB试件两端受简支约束,外载P通过刚性加载杠杆施加,加载点位于离试件中部距离为C的位置。由受力平衡可知,外载荷P可等效为试件端部张开载荷PI=PC/L及试件中部的压弯载荷PII=P(C+L)/L,进而将MMB试件等效为DCB试件与ENF试件的叠加。同时,根据加载点位置(C/L)可进一步确定裂纹扩展时I型和II型裂纹形式的混合比,m=GII/(GI+GII),0≤m≤1,即II型裂纹扩展的能量释放率(GII)与总体能量释放率(GI+GII)的比值[16, 20]。
与单一断裂模式相同,在混合模式加载的情况下,当总体能量释放率达到混合模式下的断裂韧性时,即G=GI+GII=GC,裂纹开始扩展。但混合模式的断裂韧性(GC)对裂纹混合比m的变化较为敏感,因此无法将其用作普适的裂纹扩展准则[17]。常用的替代方案为基于纯I型与纯II型的断裂韧性(GIC和GIIC)及合理的拟合参数而建立的混合模式裂纹扩展准则[23],如双参数幂准则及B-K准则[23]。因此,针对MMB试件开展裂纹扩展分析的关键在于合理地将其等效为DCB试件与ENF试件的叠加,以分别求出GI和GII。
2.1 混合型断裂叠加模型
当裂纹长度未超过试件半长时,基于线弹性及小变形假设,可将MMB试件分解为典型DCB与ENF试件,其载荷分配形式如图4所示。
由于DCB分量与ENF分量的边界条件不同,简单的叠加两者位移场所获得的MMB试件位移场不够准确。为保持DCB及ENF分量的约束与叠加后的MMB试件一致,Bennati等[20]引入DCB试件绕试件右端简支约束点的刚体转动,提出了增强梁模型(Enhanced Beam Theory,EBT),其载荷分解如图5所示,其中DCB试件的刚体转动转角θ为
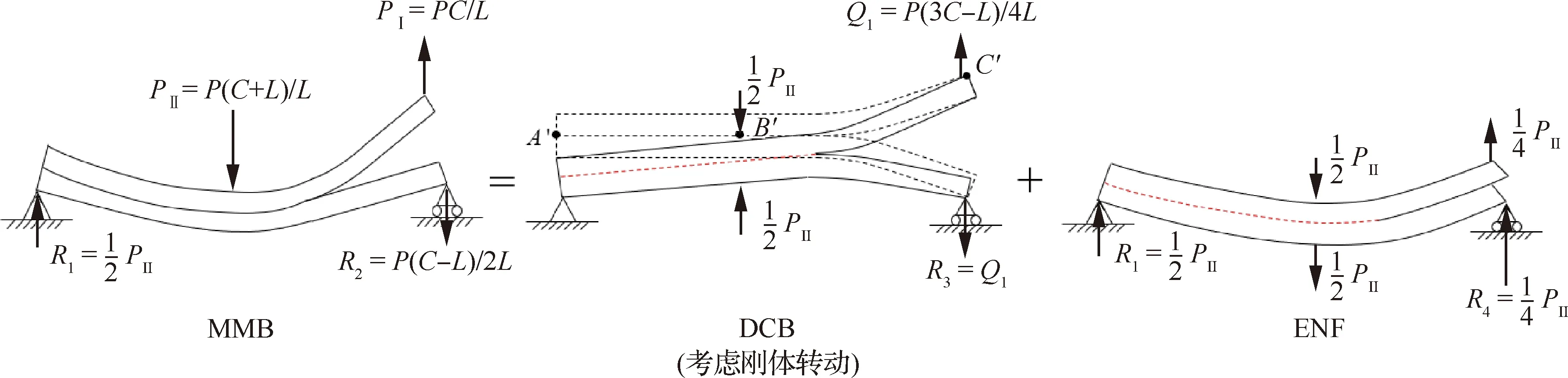
图5 考虑约束变形一致性的MMB试验载荷分解Fig.5 Load decomposition for MMB test considering consistency of constraints and displacement

(8)

(9)

(10)
式中:A11、B11分别为上半板的拉伸刚度与耦合刚度。
此外,Bennati等[20]忽略了DCB试件中PII/2分量的闭合效应对MMB试件的影响,即当裂纹长度超过试件半长时(a>L),由于PII/2分量的存在,DCB试件的I型裂纹可能会发生闭合。此时,根据DCB试件的上半板力矩平衡,MMB试件中的I型裂纹不再扩展的条件为

(11)
式中:ac为MMB试件中的I型裂纹不再扩展的临界裂纹长度。
2.2 求解
根据式(9)和式(10)给出的位移函数叠加模型,可分别对未考虑刚体转动的DCB试件及ENF试件进行求解,DCB及ENF试件的载荷及约束条件如图5所示。在裂纹扩展过程中,DCB试件及ENF试件的裂纹尖端位置应始终保持一致,且当满足裂纹扩展准则时,I型及II型裂纹同时扩展。此外,当裂纹长度超过试件半长时,由于试件中部载荷的作用,可能会出现I型裂纹完全闭合的情况,此时MMB试件中仅存在纯II型分层裂纹,本文通过判定裂纹尖端的法向相对位移是否为负值来确定I型裂纹是否闭合。
鉴于文献[13]详细分析了DCB试件的裂纹扩展过程,本文不再赘述对MMB混合断裂中I型裂纹分量的求解过程;另一方面,现有文献对ENF试件II型裂纹扩展分析仅考虑了裂纹长度小于试件半长的情况[14]。因此,本文着重对MMB试件中II型裂纹分量(ENF试件)的裂纹扩展过程进行分段求解。
3 ENF试件裂纹扩展分析
ENF试件两端受简支约束,并在其中间部位施加垂直试件表面的下压载荷。结合式(1)~式(4), ENF试件II型裂纹扩展的控制方程可简化为
(12)
式中:Δu为ENF试件上下半板的轴向相对位移;D11为上半板的弯曲刚度。
根据黏聚区本构关系,将其力学响应分为3个阶段:线弹性、黏聚区软化及裂纹扩展阶段,进而分段求解挠度函数w(x)及轴向位移函数u(x)的表达式。
(13)

(14)
式中:
φ1=
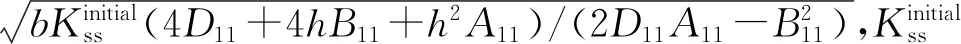
(15)
可得位移函数通解为
(16)

(17)
其位移函数的通解为
(18)
根据图3中ENF分量的载荷和约束情况,其边界条件可表示为
(19)
式中:Mreslt=M1+M2+h(N1-N2)/2为ENF试件中关于中面(断裂面)的合力矩。
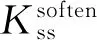
初始裂纹长度。在xE=2L-a-lCZ、xS=2L-a,ENF试件的位移函数w(x)、u(x)均应满足位移连续、转角连续、合力矩连续、剪力及轴力连续条件:

(20)
(21)
式中:Qreslt为上下半板的合剪力。因此,由边界条件式(19)及连续性条件式(20)、式(21)即可确定位移函数w(x)、u(x)中的24个待定系数ai(i=1,2,…,24)。
黏聚区尖端xE=2L-a-lCZ处的位移应始终保持为Δs(xE)=Δonset,由该约束条件即可求得载荷P的值。进一步地,在数值计算过程中,设定黏聚区长度lCZ为增量叠加的过程:
(22)
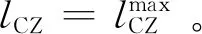
特别地,在加载点处,存在集中载荷P,引起剪力突变,其突变的绝对值为载荷P的大小,即为
P+Qreslt(L-)=Qreslt(L+)
(23)
令Δs(xE)=Δonset,可求得加载时线弹性阶段的最大载荷P0。
当黏聚区满足裂纹扩展条件时,即Δs(xS)=Δultimate,裂纹发生扩展,此时裂纹长度a>a0。在数值计算过程中,设定裂纹长度a为增量叠加的过程:
aj=aj-1+δa
(24)
式中:δa为裂纹长度增量,本文取为0.001 mm。此外,在裂纹扩展过程中,裂尖点xS=2L-a处及黏聚区尖端xE=2L-a-lCZ处的位移应满足以下约束条件:
(25)
4 分析与讨论

(26)

此外,考虑AS4/PEEK为热塑性复合材料,本文采用B-K准则作为裂纹扩展准则。
由于假设加载杠杆为刚性,在试验过程中不发生变形,则MMB试件加载点的位移ΔP可由端部位移Δend及试件中部位移Δcenter的约束关系得到[24-25]:
(27)
为验证本文MMB试件裂纹扩展分析模型的合理性及有效性,将不同混合比下载荷-位移曲线的预测结果与文献[24]中的试验结果进行对比,如图7所示。可见,本文提出的基于CZM裂纹扩展分析模型能较好地模拟I-II混合型裂纹扩展过程,所得的载荷-位移曲线与试验结果吻合较好。
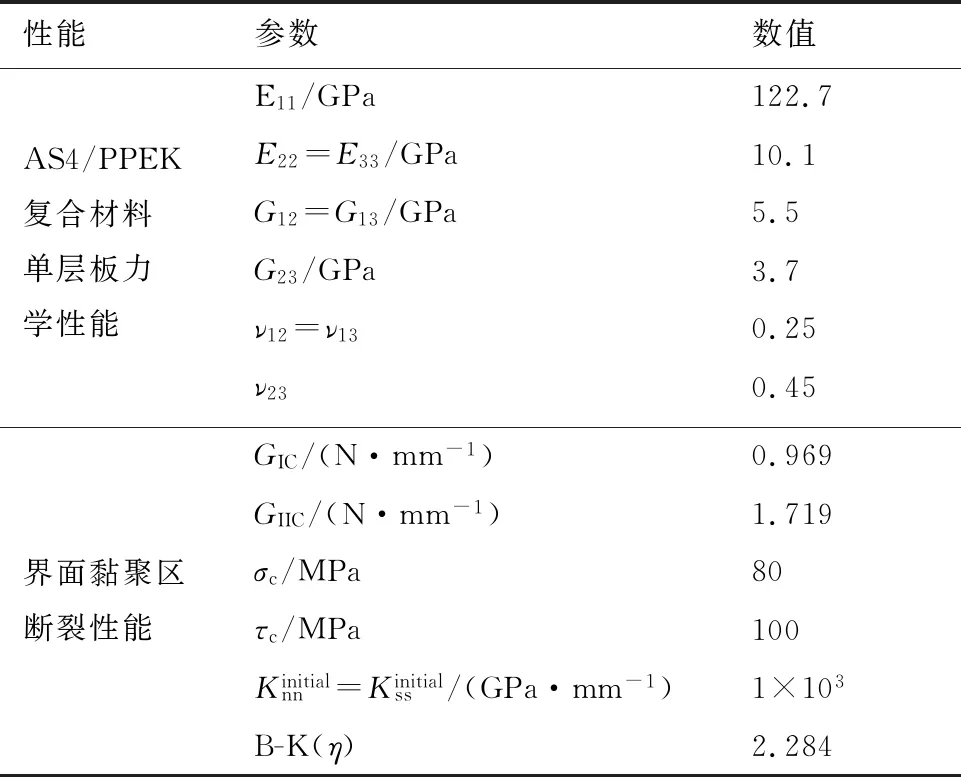
表1 MMB试件材料力学性能参数[24-25]Table 1 Material properties of MMB test specimens[24-25]

表2 不同混合比下MMB试件的几何尺寸[24-25]

图7 MMB试验分层裂纹扩展载荷-位移曲线Fig.7 Crack propagation in MMB tests: load vs displacement curves
图8给出了不同初始混合比下的MMB试件失效载荷预测值与试验值对比结果,图中Pc为最终破坏载荷。由于考虑了黏聚区的软化过程,本文模型的载荷-位移曲线在初始弹性加载段之后引入非线性,使得最终的失效载荷预测小于增强梁模型的结果,更为接近试验值。此外,随着II型裂纹比重的增加,在达到失效载荷之后,持续加载,II型裂纹主导的分层破坏使得MMB试件的结构刚度降低更快。

图8 MMB试件失效载荷预测值与试验值对比Fig.8 Comparison between model prediction and test results of failure loads in MMB tests
不同初始混合比下,图9给出了MMB试件端部(x=2L)相对位移及中部(x=L)变形随载荷变化的响应结果。对比3种初始混合比下的试件中部变形Δcenter随载荷增加的变化情况,可以发现II型裂纹比重较低时,Δcenter在裂纹开始扩展之后出现一定程度的负值(假定结构向下变形为正),如图9(a)、图9(b)所示。由式(10)可知,DCB分量张开的向上位移大于ENF分量产生的向下压弯变形,表明此时I型裂纹是主要的分层损伤形式。初始混合比值GII/GT较大、悬臂长C较小时,如图9(c)所示,试件的端部相对位移Δend也随之减小,其对Δcenter的约束作用降低,使得Δcenter在整个裂纹扩展过程中始终保持为正值,表明试件更多地产生II型裂纹。

图9 不同初始混合比下的MMB试件中部及端部位移响应结果Fig.9 Center and end displacement responses of MMB specimens at different initial mode mixity ratios

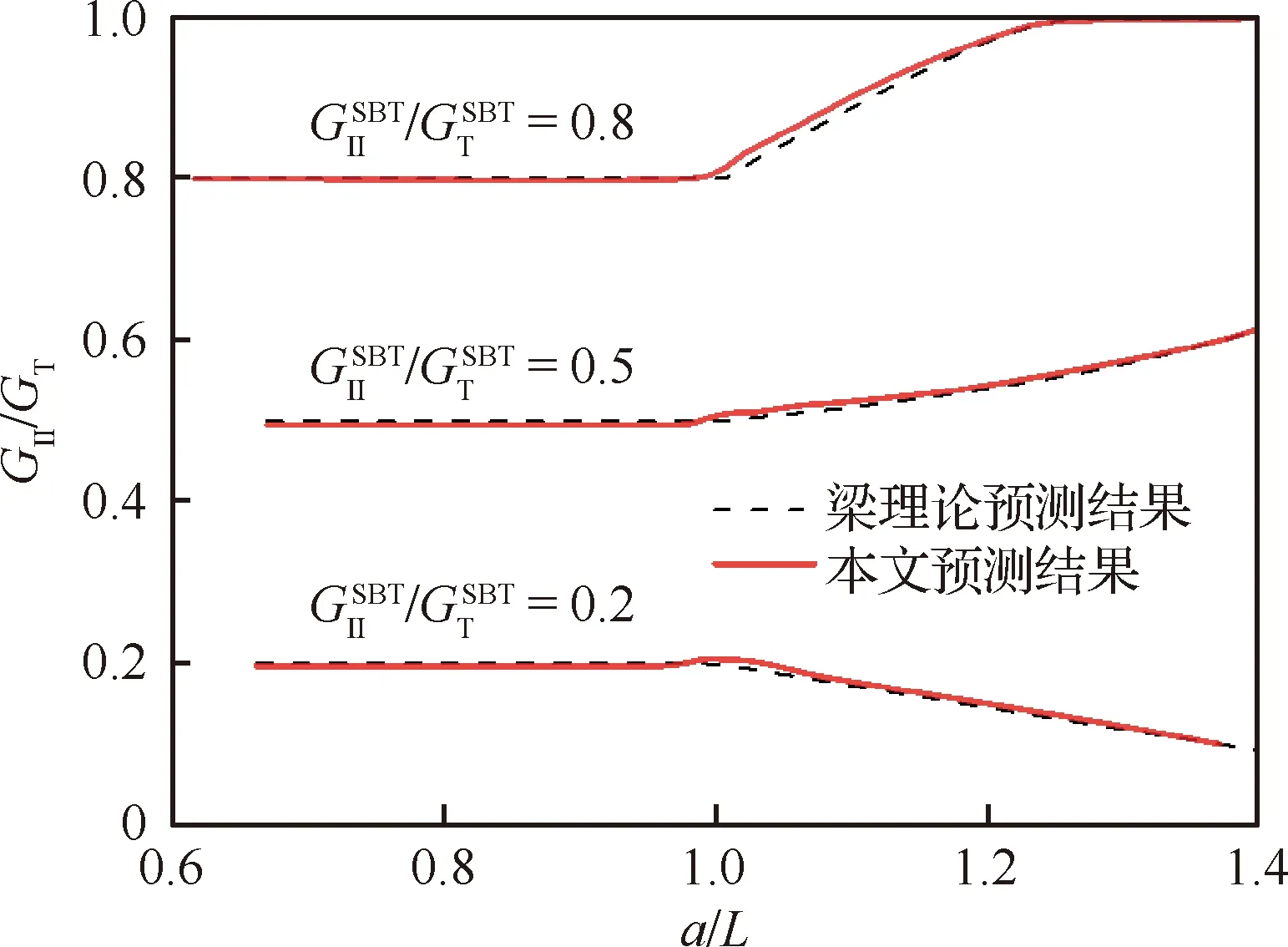
图10 MMB试验中混合比随裂纹扩展的变化趋势Fig.10 Variation trends of mode mixity ratio with crack propagation in MMB tests
5 结 论
基于经典层合板理论及双线性黏聚区本构形式,针对对称铺层MMB试件的裂纹扩展过程,建立了I-II混合型断裂的裂纹扩展理论模型,引入黏聚区的软化行为,同时在裂纹叠加模型中考虑了I型裂纹分量的刚体转动位移及中部载荷的闭合效应,得到了以下结论:
1) 与梁模型预测及试验结果进行了对比,验证了其有效性和准确性。
2) 针对II型裂纹分量,给出了裂纹大于试件半长后ENF试件位移函数的分段通解。
3) II型裂纹的初始混合比较大时,闭合效应更为明显,可能出现I型裂纹完全闭合的情况。
4) 裂纹扩展过程中,当裂纹长度小于试件半长时,断裂混合比基本为常数,随着裂纹扩展超过试件半长,由于中部载荷的闭合效应,裂纹形式逐渐向初始比重较大的单一型断裂退化。
本文研究了I-II型混合断裂对称铺层MMB试件的裂纹扩展,后续工作应进一步分析多种混合型断裂韧性试件的裂纹扩展,同时考虑铺层方式与不同黏聚区本构形式对裂纹扩展的影响,提高预测的准确性及模型的适用性。
[21] REDDY J N. Mechanics of laminated composite plates and shells: Theory and analysis[M]. Boca Raton: CRC Press, 2004.
