类X-37B航天器气动力天地相关性数值模拟

马率，张露，刘钒，孙俊峰，崔兴达

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

跨大气层飞行器气动特性的复杂性在于飞行走廊(即飞行轨道)的参数非常复杂，包括离地高度、马赫数、迎角、侧滑角等流动参数和副翼、升降舵、方向舵、襟翼偏角等控制参数，单纯依靠风洞和飞行试验的手段从耗费、时间等角度来说远不能满足需求。而航天飞行器相比航空飞行器的风洞试验更加困难、外形较简单更适合CFD计算，CFD高效批量生产数据的特点可以对试验数据进行补充，尤其是对地面数据向真实飞行条件的修正与外推的天地相关研究工作具有重要意义[1]。

X-37B是波音公司为竞标美国空军“轨道飞行器项目”而研制的无人且可重复使用的跨大气层在轨飞行器，该机由火箭发射进入太空，是第一种既能在环绕地球卫星轨道上飞行又能自主重返大气层并最终着陆的航天飞行器，截至2014年10月17日，X-37B(OTV3)已完成连续飞行超过674天[2]。

波音公司设计的X-37B特点有：机翼由细长边条翼和后部短小三角翼组合而成双三角翼，机翼后缘设计有全展长的襟副翼、机体上部有一对集方向舵和升降舵作用的V型尾翼、V尾中间有减速板，机体后带有体襟翼，飞行器腹部为平面的翼身组合体布局(也称升力体布局)[3]，见图1。X-37B的气动特性研究主要包括风洞试验(见图2)、数值模拟和飞行试验3个方面，根据波音公司的报告，X-37的风洞试验数据只占了研发与创建用于再入飞行的气动数据库的19%，剩下的绝大部分采用数值计算方法，只有小部分是用飞行试验来验证地面试验和数值计算结果，弥补地面试验的不足[4]。鉴于X-37B项目的成功，国内也先后采用了CFD技术对此类飞行器开展了布局概念设计[5]及气动特性研究[6]。

图1 X-37B的气动控制面[3]Fig.1 Aero-surfaces of X-37B[3]

图2 AEDC风洞中的X-37B气动试验Fig.2 Aerodynamics tests of X-37B in AEDC wind tunnels

为了研究类X-37B布局航天器风洞试验与飞行数据的天地相关性问题，建立了类X-37B航天器相关模型，然后开展了计算模型网格的规模影响及修正研究，在此基础上对比分析了雷诺数和试验状态支架干扰的影响，完成了类X-37B航天器气动力天地差异性分析，以期为今后开展相关研究积累技术基础。

1 计算模型及数值方法

参照已公布的X-37B外形信息及风洞试验图片，生成了类似X-37B的飞行器模型和带支杆1∶24的缩比模型，见图3。计算网格分为真实构型和带尾支撑杆的缩比模型,真实构型的第1层网格距离物面的距离为5×10-6m，而缩比模型的第1层网格距离物面的距离相应为2.3×10-7m，这两个距离在马赫数范围(Ma=0.4～8.0)、离地高度55 km以下都能达到0.3≤y+≤5,围绕飞行器生成的是C型对接网格，在保持相同物面距离的条件下，网格规模在研究网格无关性时为1 000万 ～8 000万。在不同雷诺数和试验状态支架干扰的影响研究中采用的网格规模为1 000万，有关网格规模对计算结果的影响将在下文做详细说明。图4给出了飞行器的相关计算网格。

图3 类X-37B基本模型及带支杆缩比模型Fig.3 X-37B-like base model and model with wind tunnel strut

图4 类X-37B基本模型及带支杆缩比模型计算网格Fig.4 Computational grid of X-37B-like base model and model with wind tunnel strut

计算采用笔者所在课题组自主研发的并行多块结构化网格的数值计算PMB3D求解器[7-8]完成，该程序目前已经升级到了9.0版本，在国内航空航天领域多个复杂流动工程项目的计算模拟中得到了应用与验证[9-12]。本文数值模拟应用了有限体积法求解Navier-Stokes方程，在惯性坐标系下的积分形式为

(1)

式中：状态变量Q=[ρ,ρu,ρv,ρw,e]T用守恒变量表示，分别代表流体的密度、动量分量和总能；HI表示控制体边界面上的对流通量；HV表示黏性通量；Ω表示控制体的体积；S表示控制体边界面的面积；n为边界面的外法向量。计算中黏性项采用中心差分，无黏项采用Roe平均迎风通量差分分裂格式离散，选取Condiff限制器来保证将网格单元格心物理量插值到界面处的精度及鲁棒性，时间格式采用了隐式LU-SGS方法，湍流模型选取了考虑可压缩修正的Menter’sk-ωSST两方程模型，并运用了多重网格、残值平均和局部时间步长、并行加速等高效计算方法。

2 网格规模影响及修正

2.1 网格规模差异对计算结果影响

保证足够大的网格规模对提高计算结果可信度是十分重要的，这里采用从1 000万、2 000万、3 000万、 5 000万直至8 000万网格规模，对类X-37B布局的飞行器网格无关性计算做深入研究。图5给出了1 000万和8 000万网格规模的表面网格比较。以Ma=0.4，迎角α=0°，4°，8°为例，研究网格对纵向气动特性的影响。图6给出了气动系数随网格规模的变化趋势，其中，N为网格格心点数，1/N2/3为AIAA阻力预测会议(Drag Prediction Workshop, DPW)[13-14]归纳的研究气动力预测精度与网格变化关系的参数。

图5 不同网格规模的物面网格比较Fig.5 Comparison of different sizes of surface meshes

由图6可见，轴向力系数Cx随1/N2/3减小基本上线性下降，而法向力系数CN、俯仰力矩系数Cmz随1/N2/3减小变化很小。图6中纵坐标数值是轴向力系数随1/N2/3的线性关系推出的采用PMB3D软件计算Ma=0.4，α=0°、4°、8°状态得到的轴向力系数Cx理论网格收敛值。为进一步研究亚跨超范围内采用1 000万网格和8 000万网格对计算结果的影响，图7给出了1 000万网格相对8 000万网格计算0°迎角时轴向力系数Cx和摩阻系数Cf随马赫数变化曲线，可见在亚跨声速时，两套网格的轴向力计算结果差别较大，在马赫数0.4时误差最大为32.4%，在马赫数1.05以后误差不到5%，而两套网格的摩阻系数计算结果差别较小，最大误差不到6%。另外两套网格在亚跨超范围内法向力系数的误差最大为2.05%， 俯仰力矩系数的误差最大为1.95%，纵向压心的误差不超过0.7%机身长度。

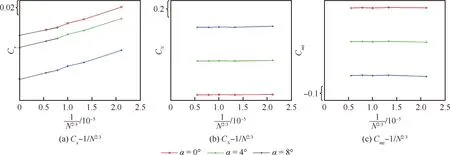
图6 气动系数随网格数的变化趋势(Ma=0.4，β=0°,Re=7.91×107)Fig.6 Varying trends of aerodynamic coefficients with grids (Ma=0.4，β=0°,Re=7.91×107)

图7 α=0°时网格数对Cx和Cf的影响及相对误差Fig.7 Influence of grid numbers on Cx and Cf and relative error at α=0°

综上所述，亚声速来流计算状态网格规模对由压差产生的轴向力影响较大，对法向力系数、俯仰力矩系数和纵向压心影响很小。

2.2 网格影响修正

2.1节研究表明，采用密网格计算的轴向力系数明显比稀网格计算的合理可信，但采用密网格耗费的计算机资源庞大，比如8 000万网格比1 000万 网格的计算机资源占用大出近一个数量级。因此，研究稀网格和密网格计算结果差异的规律性，并运用规律将稀网格的计算结果修正到理论网格收敛值上来是十分有意义的。

研究轴向力系数与迎角的变化趋势可以发现1 000万网格计算的轴向力系数与8 000万网格计算的轴向力系数之间的差异基本上与迎角无关，前体轴向力系数和底部轴向力系数也存在类似的关系。因此可以用表1中0°迎角8 000万网格与1 000万网格计算的轴向力系数之差、前体轴向力系数之差和底部轴向力系数之差作为修正量，来修正1 000万网格计算结果中的轴向力系数、前体轴向力系数和底部轴向力系数，升力系数、阻力系数和升阻比根据轴向力系数和法向力系数对不同迎角的投影而重新计算，其他气动系数由于随网格规模变化基本上在2%以内，不做修正。

由于篇幅所限，图8只给出了在亚跨声速范围1 000万网格、8 000万网格和1 000万网格修正计算得到的轴向力系数Cx、底部轴向力系数Cxb。由图可见，1 000万网格修正后的结果与8 000万网格的计算结果基本重合，说明以上修正方法是可信的，在工程上也是非常实用的。

表1 α=0°时网格影响修正量Table 1 Grid influence correction at α=0°

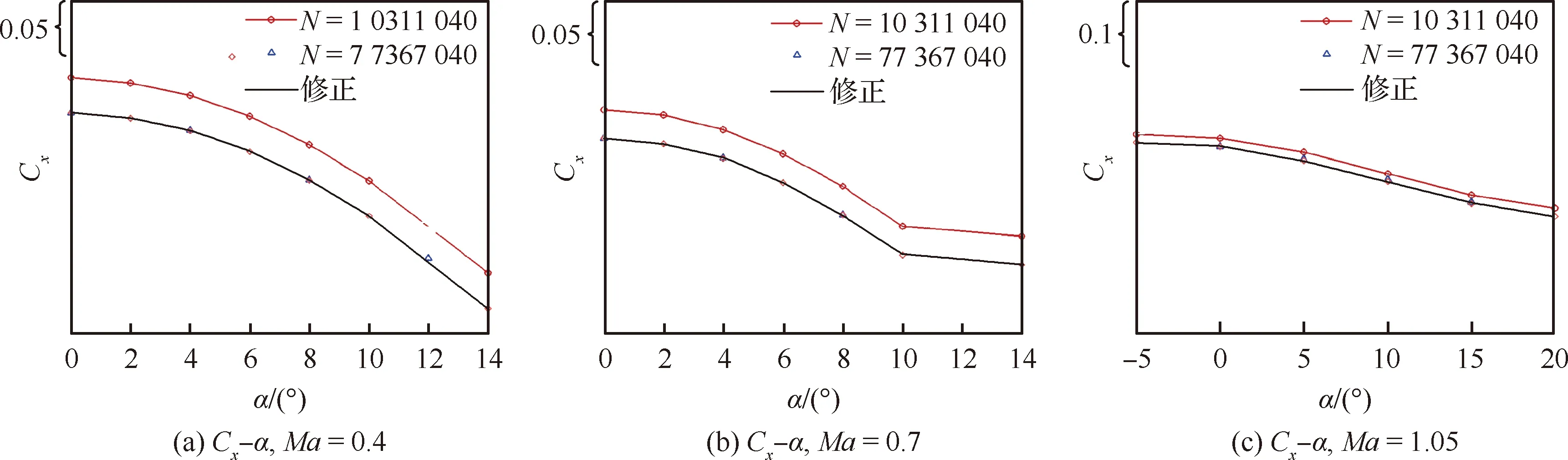
图8 修正后气动特性与采用1 000万、8 000万网格计算结果比较(β=0°，δ=0°)Fig.8 Comparison between correction aerodynamic coefficients and calculation results with 10 million and 80 million grids (β=0°，δ=0°)

3 高空飞行与风洞试验气动差异

3.1 雷诺数对基本外形的气动特性影响

分别按飞行雷诺数和风洞试验雷诺数计算类X-37B飞行器无舵偏无侧滑的气动特性，这里气动特性计算仍然使用1 000万网格并采用了第2节中的网格修正方法来修正相关的气动力结果，高空飞行与风洞试验雷诺数的比较见图9,可见高空飞行雷诺数都要大于风洞雷诺数[15]。

飞行雷诺数、风洞试验雷诺数和风洞试验雷诺数带支杆三者的气动特性部分计算结果见图10。 结果表明在亚跨声速来流时，雷诺数增大使法向力系数CN、升力系数CL和俯仰力矩系数Cmz的绝对值略有增大，随着马赫数增加，雷诺数影响逐渐减小，在高超声速时雷诺数影响量又开始微幅增大。在亚跨声速来流时雷诺数增大使轴向力系数Cx和阻力系数CD明显减小，随着马赫数增加雷诺数的影响量减小，在高超声速时雷诺数影响量又开始略有增大。在所计算的马赫数范围内除0°迎角外雷诺数增大使压心略有后移，但最大后移量不超过机身长度的0.5%。在亚跨声速范围内由于雷诺数对轴向力和阻力系数影响较大，因此雷诺数对此范围内的升阻比影响较大，雷诺数增大使升阻比增大，最大变化在Ma=0.4、α=10° 处，增大量为0.586 22。

图9 高空飞行雷诺数与地面风洞试验雷诺数比较Fig.9 Comparison of Reynolds number of high altitude flight and ground wind tunnel test

在真实风洞试验中，测量得到的模型阻力是很难将摩擦阻力和压差阻力分开并区分准确的，而CFD的优势之一就是能将计算得到的阻力分解为压差阻力和摩擦阻力，这就为飞行器的阻力特性分析提供定性和定量的优势。为研究雷诺数对阻力系数的影响，采用CFD方法对真实飞行状态和试验工况状态的0°迎角阻力系数CD进行了数值模拟，并将其分解为压差阻力系数CDp和摩擦阻力系数CDf，以各自飞行雷诺数的Cx作为归一化系数，它们的构成见表2，可以看到在亚声速阶段，摩阻能占到阻力的近30%，随着马赫数的增大所占比重急剧减小，到Ma=7.0时已不超过阻力的5%。另外飞行和风洞试验的雷诺数差异对压差阻力和摩擦阻力都有一定的影响。根据附体流动的一般规律，雷诺数增大使摩擦阻力系数减小，由于Ma=0.4 飞行雷诺数与风洞试验雷诺数差异最大，因此在Ma=0.4时雷诺数对摩擦阻力系数影响最大。但在Ma=5.0，7.0时，雷诺数的增大并没有使摩擦阻力系数减小，这是因为按风洞雷诺数计算时物面分离导致的，由于风洞雷诺数的边界层厚度相比飞行雷诺数的变厚，机身上的流动顶着逆压梯度前进的能力变弱，风洞雷诺数相比飞行雷诺数在机身上更容易分离，而分离区内靠近壁面的流动实际上变为回流或逆流，导致物面的摩擦力相比未分离时反向，与飞行器总摩擦力方向相反，产生了类似附加推力的作用。图11给出的是Ma=3.0、Ma=7.0按飞行雷诺数和风洞试验雷诺数计算的对称面流场等马赫数图，在Ma=3.0时按两个雷诺数计算的流场没有分离，而在Ma=7.0时可以看到按风洞雷诺数计算的流场机身前体已经明显分离。

进一步把压差阻力CDp分解为前体压差阻力CDfp和底阻CDd，由表2可见，在亚跨声速时，雷诺数对前体压差阻力系数有一定的影响，一方面雷诺数对底部分离流动的影响会传到上游流动，从而改变上游流动的压强分布；另一方面雷诺数对附面层厚度的影响会导致跨声速激波位置的变化从而引起波阻改变。而在超声速时，由于雷诺数对底部分离流动的影响不会传到上游流动，所以雷诺数对前体压差阻力系数的影响非常小。在高超声速时，由于飞行器前体流动分离，使雷诺数的影响分析更加复杂。

图10 雷诺数及有/无支杆对气动特性影响比较(β=0°，δ=0°)Fig.10 Comparison of influence of Reynolds number on aerodynamic characteristics with and without support sting (β=0°，δ=0°)

表2 迎角0°时基于CFD计算结果的雷诺数对阻力系数的影响分析(归一化)Table 2 Re influence correction of CD base on CFD results(normalization) at α=0°

图11 雷诺数对流场的影响(α=0°)Fig.11 Effects of Reynolds number on flow fields (α=0°)

3.2 有/无支杆对基本外形的气动特性影响

模型支杆的气动干扰问题自风洞试验诞生以来就成为阻碍模型风洞试验精准度提高的难题。从更广义的角度上看,由于模型支杆破坏了试验模型的有效外形和支杆本身的绕流特性，干扰了试验模型的流场，这两方面的因素改变了按飞行器外形几何相似缩小的试验模型的空气动力学特性[16]。

目前风洞试验结果都是扣除了带尾支杆影响在内的底部阻力或底部轴向力，这就是试验中常被提及的“前体阻力”或“前体轴向力”，扣除了底阻的带尾支杆支撑的模型风洞试验,很难准确给出依赖于总阻力或总轴向力的试验模型的配平迎角和相关力矩，因此对支杆影响的修正在风洞试验中不可忽视。

本节按风洞试验雷诺数分别计算了有/无支杆情况下的气动特性[17-18]，并通过比较两者之间的差异分析支杆的影响。支杆外形尽量模拟风洞试验的支杆，见图3，值得指出的是，为了使带支杆外形的底阻计算与对应的无支杆外形保持一致，真实风洞中对应的风洞试验底阻计算一般是通过支杆在底部附近布置的n个采样测压点的压强平均获得的，具体为

(2)

式中：CpA、CpB…CpN分别为支杆在底部1～n个测压点的压力系数；Sb为无支杆外形的完整底部面积；Sref为计算参考面积。这样带支杆外形轴向力系数计算值就修改为

(3)

由图10可见，支杆对升力系数CL和俯仰力矩系数Cmz影响不明显，对阻力系数CD影响较大，在亚跨声速来流时，支杆的存在使轴向力系数和阻力系数减小，随着马赫数增大，支杆的影响量逐渐减小，特别是超声速和高超声速，由于下游流动不能向上传递，因此除0°迎角支杆的存在使升阻比增大外,其他状态下支杆的影响量很小。

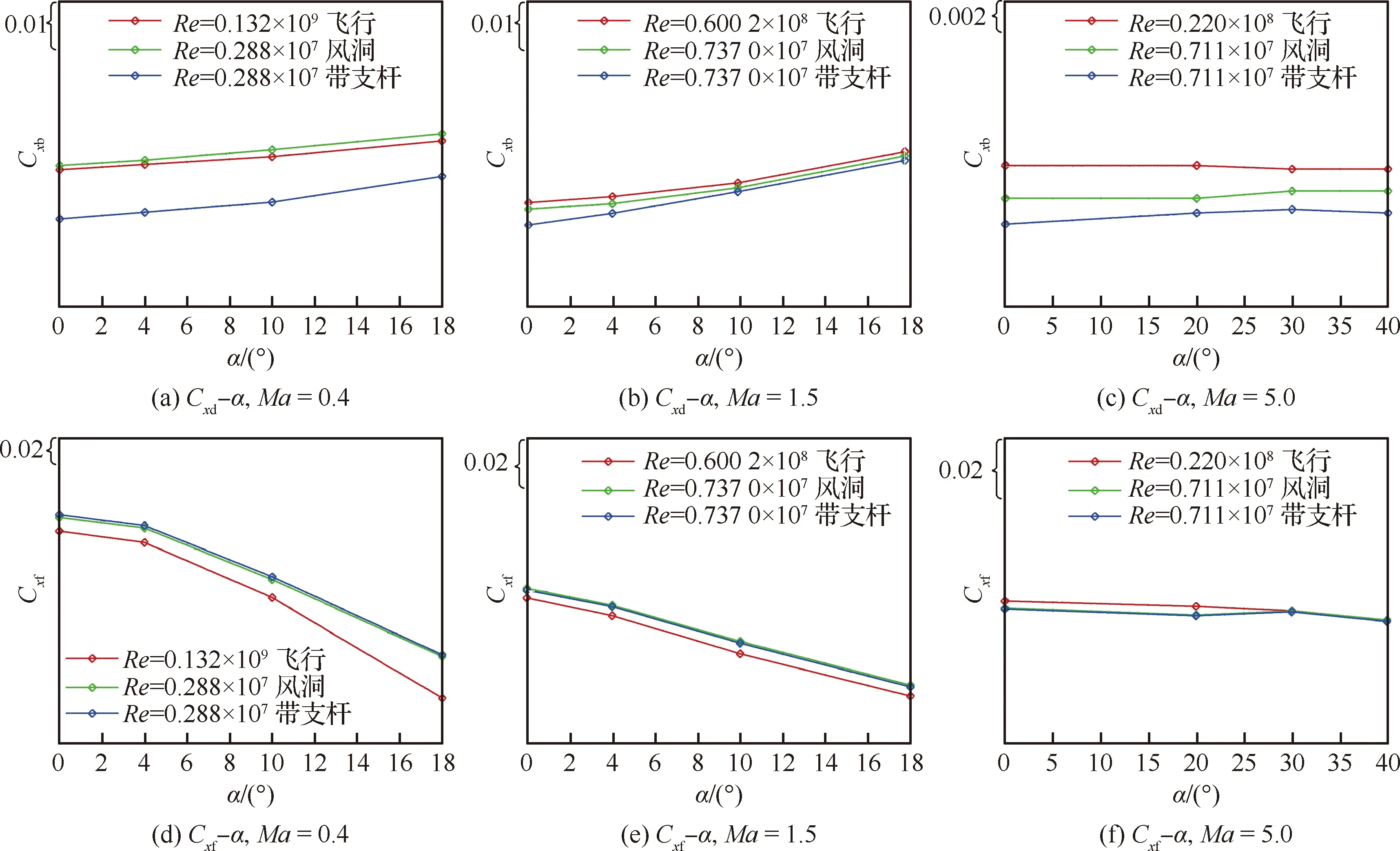
图12 底部轴向力系数和前体轴向力系数在有/无支杆情况下比较 (β=0°，δ=0°)Fig.12 Comparison of Cxb and Cxf with and without support sting (β=0°，δ=0°)

图13 底部测压点示意图Fig.13 Diagram of bottom pressure measuring points

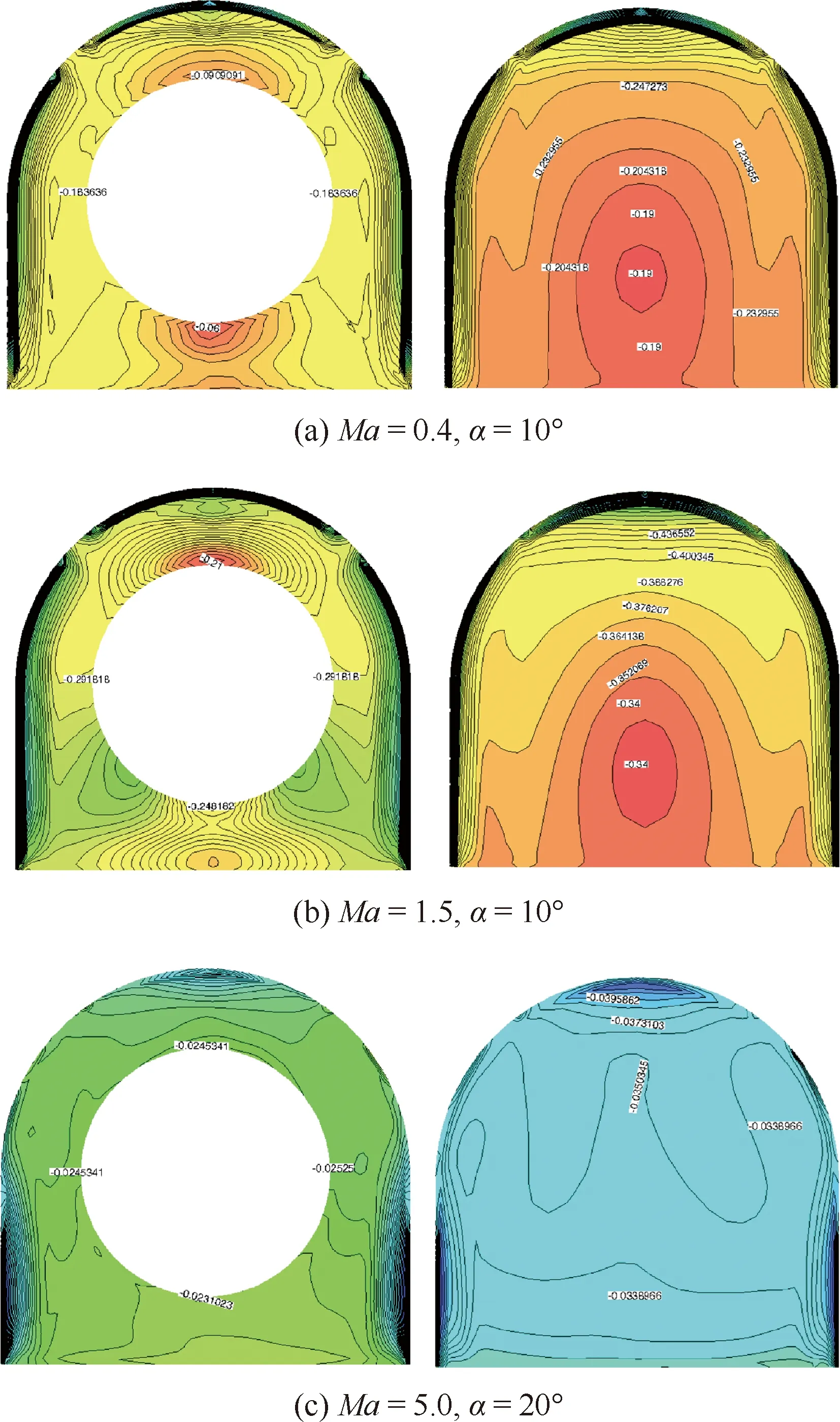
图14 有/无支杆外形底部压强分布比较Fig.14 Comparison of bottom pressure distribution with and without support sting

4 结 论

本文采用数值模拟方法研究了网格规模对类X-37B布局航天器数值计算结果的影响，获得了不同网格规模对纵向气动特性的影响规律，探讨了实用于工程的网格规模影响修正方法，通过对该布局飞行器高空飞行和风洞试验状态数值计算数据分析和研究，得到以下结论：

1) 不同网格规模对类X-37B气动布局航天器的亚声速轴向力系数影响较大，对法向力系数、俯仰力矩系数和纵向压心影响不大。

2) 不同网格规模对轴向力系数的影响基本上与迎角无关，本文提出的网格规模影响修正方法对类X-37B气动布局飞行器的计算结果修正是可信的，在工程上也是非常实用的。

3) 由于风洞试验模型缩比较大，特别是在亚跨声速风洞试验雷诺数与高空飞行雷诺数差一个量级，因此雷诺数对类X-37B气动布局飞行器气动特性特别是轴向力系数、阻力系数和升阻比有较大的影响。

4) 由于风洞试验状态支杆的存在，在亚跨声速来流时对类X-37B气动布局飞行器底阻影响较大，因而对此类飞行器轴向力系数、阻力系数和升阻比有较大的影响。

5) 在本文研究范围内，雷诺数和支杆对类X-37B气动布局飞行器的轴向力系数影响趋势相反，从而使高空飞行与风洞试验状态轴向力系数的差异缩小。