缝合复合材料T型接头拉伸载荷下的有限元数值模拟
2021-03-26文立伟余坤宦华松
文立伟,余坤,宦华松
南京航空航天大学 材料科学与技术学院,南京 210016
缝合复合材料T型接头在拉伸载荷下,接头筋条与蒙皮变形程度较大,缝线受力情况复杂,使得T型接头失效机理分析较为复杂[1-2]。近年来,国内外学者通过理论[3]、试验[4]及数值模拟[5]的方法针对复合材料缝合件进行了广泛研究。
缝合的应用最早是为解决层合板的分层问题,20世纪80年代,Mignery等[6]将碳纤维缝入了层合板,结果显著提高了层合板的层间强度,提高了层合板厚度方向的承力作用。Velmurugan和Solaimurugan[7]研究了缝合与未缝合玻璃纤维增强复合材料的层间断裂韧性以及面内纤维取向对I型层间断裂韧性的影响。朱华东等[8]研究了缝合密度和缝线直径对缝合复合材料层合板 Ⅱ 型层间断裂韧性和分层模式的影响。目前,简单缝合层合板的研究已相当成熟,在缝合层合板的基础上,缝合T型接头将上部筋条与下部蒙皮连接起来,不仅要考虑铺层层间性能,还要考虑筋条-蒙皮连接界面的界面性能。张国利等[9]在试验研究BS3-94-10型环氧树脂性能和缝合件层间剪切和弯曲性能的基础上,优化设计了树脂膜融渗技术和缝合工艺参数,制备了高性能T型加筋壁板试样。经测试,缝合后T型加筋整体壁板平均临界屈曲强力、平均破坏强力、正面和背面相同位置上最大破坏应变分别增加24.6%、18.3%、21.2%和24.6%。此外,Kim等[10]采用一种新的单线缝合工艺制备T形接头,使碳纤维的弯曲程度最小化并防止其断裂。拉伸试验结果表明:缝合纤维密度为0.5%和2%的T型接头的破坏载荷相比未缝合试样提高40.56%~47.47%,并且高于相同增强纤维密度下的Z-pin试样。当前,国内外关于缝合复合材料的数值模拟研究,主要集中于缝合层合板。叶强和陈普会[11]从复合材料的细观结构出发,提出了用于预测粘聚区模型的强度参数的细观模型, 以提高有限元法模拟复合材料分层的精度。孔斌等[12]利用三维有限元模型研究了Z-pin/缝合增强试验件的剪切承载能力,指出应选择拉伸强度较高而拉伸模量较低的缝线来进行缝合增强设计。Iwahori等[13]利用二维有限元模拟了缝合层合板和三维正交互锁织物的双悬臂梁(DCB)试验结果,建立了这2种复合材料分层扩展的力学模型。针对复合材料T型接头的仿真研究多见诸于Z-pin增强件,李梦佳等[14]建立了Z-pin增强T型接头的二维平面应变模型,研究了Z-pin参数对T型接头拉伸性能的影响。Grassi和Zhang[15]在DCB模型中,将Z-pin模拟成只连接上下悬臂梁胶接界面的非线性界面元,发现当脱胶扩展至Z-pin布置区域后,Z-pin能有效地抑制脱胶。
以往的研究更加关注缝合层合板的力学性能[16-18],而复合材料T型结构受自身形状以及筋条-蒙皮间连接界面的影响,在外部载荷下的受力情况与损伤失效行为更加复杂[19]。当前针对缝合T型接头的研究又大多集中于试验分析,极少涉及参数化的数值模拟。本文利用ABAQUS有限元软件对拉伸载荷下的缝合T型接头进行了建模与分析,通过对比有限元结果与试验值,验证了分析方法的可靠性。在此基础上,对缝线进行参数化分析,研究缝合参数对T型接头拉脱承载能力的影响,总结缝线增强规律。研究结果对复合材料T型接头的缝合增强设计具有一定的指导意义。
1 建 模
1.1 材料与试验
缝合T型接头试样的几何尺寸如图1所示,宽度为40 mm,结构由蒙皮、两片筋条及填充物组成。筋条铺层为[0/90]2S,厚度为1 mm;蒙皮铺层为[0/90]4S,厚度为2 mm。结构采用T700/RTM 3312A复合材料,填充区(R区)材料与主体结构相同,材料性能如表1所示。筋条与蒙皮连接区域为缝合区,缝线为Kevlar-29纤维,性能见表2。实验加载速率为0.5 mm/min,加载跨距为120 mm,拉伸试验加载装置如图2所示。

图1 缝合T型接头试样几何构型Fig.1 Geometry of stitched T-joint sample

表1 T700/RTM3312A复合材料的力学性能Table 1 Mechanical properties of T700/RTM3312A

表2 Kevlar-29缝线力学性能Table 2 Mechanical properties of Kevlar-29

图2 拉伸试验加载示意图Fig.2 Schematic of loading of tensile test
1.2 基于内聚力模型的界面模拟方法
内聚力模型(Cohesive Zone Model, CZM)是对复合材料界面行为的简化。黏聚接触行为(Cohesive Behavior)基于内聚力模型,通过定义破坏准则模拟裂纹萌生和扩展,能清楚表现损伤起始和分层扩展,其参数包括能量释放率、界面强度和界面刚度值等力学特征。本文采用双线性内聚应力-相对位移(Traction-Separation,T-S)关系,如图3[20]所示。图中,K为刚度,τ0为单元失效强度,Δf为失效位移,Δ0为发生初始破坏时的位移,GC为单元临界能量释放率(即断裂韧性),D为单元损伤系数,当D=1时,单元出现损伤。
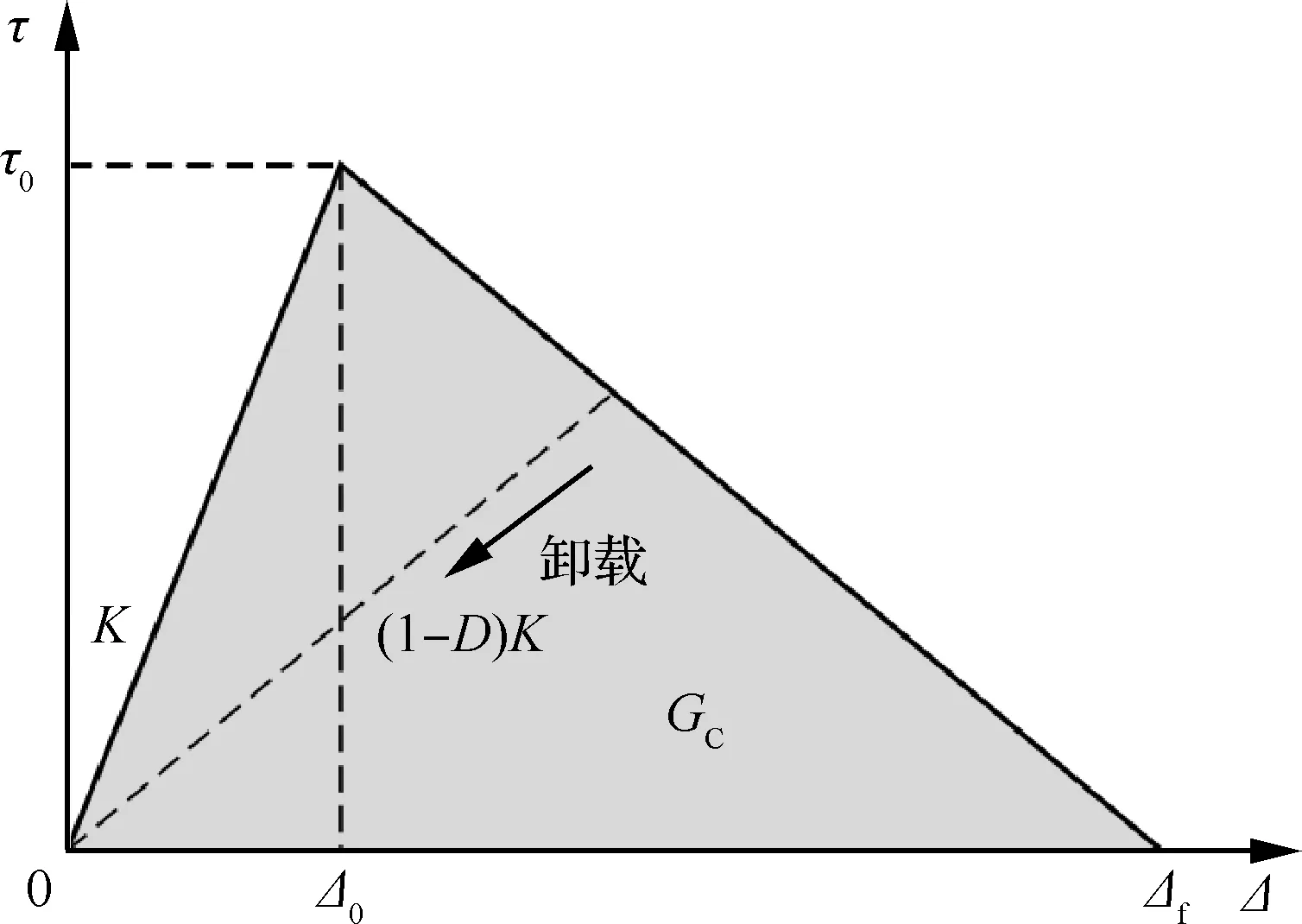
图3 内聚力双线性本构模型[20]Fig.3 Bi-linear constitutive model of cohesion[20]
T型接头筋条-蒙皮连接界面在裂纹的演化及失效过程中受 I/Ⅱ 型混合应力[21-22],因此界面的损伤破坏准则采用BK(Benzeggagh-Kenane)混合准则:
(1)
(2)
式中:GⅠC、GⅡC分别为 I、Ⅱ型临界应变能释放率;GⅠ、GⅡ分别为 I、Ⅱ型断裂应变能释放率;η为损伤因子,一般在0.5~3之间,本文取2。
1.3 缝线桥联律
缝线的桥联律即分层处桥联力T和相对位移δ之间的关系,缝线在层间作用时,不仅会产生法向拉伸变形,还会受到剪切作用,发生横向变形。图4所示是缝线在基体内的变形拔脱图。当缝线被拉伸到层合板的表面时,由于缝线受到底部缝线的拉扯作用,缝线不会立刻离开表面,此时桥连力T也会继续增大直到缝线断裂。当缝线在界面断裂,会出现急剧掉载,随后剩余缝线开始被拔出;当缝线在裂纹处断裂,缝线急剧掉载到零。
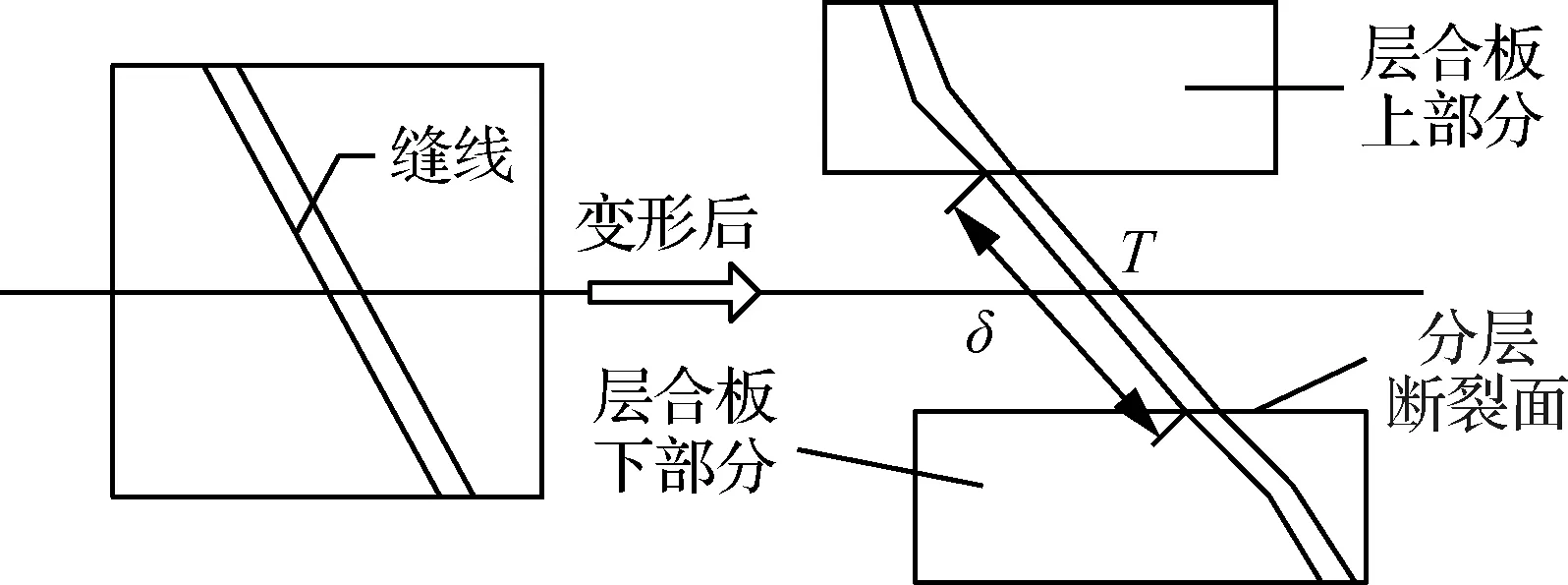
图4 缝线在层间受力示意图Fig.4 Stress diagram of thread between layers
缝线直径不同,其桥联律也不同。缝线直径通常用“旦尼尔(Denier)”来表征,指9 000 m长的纤维在公定回潮率时的质量克数,单位为旦(D),D值越大表示缝线越粗。Kevlar-29缝线的桥联律通过细观力学法计算得到,如图5所示。

图5 缝线的桥联律Fig.5 Bridging law of thread
2 未缝合T型接头三维模型分析
根据T型接头实际尺寸建立三维模型,结合夹具夹持位置,将立筋高度取为35 mm,蒙皮长度取为120 mm,宽度不变仍为40 mm。将蒙皮两端固定,筋条上端施加位移载荷,蒙皮两端约束U1、U2、U3自由度,以防止蒙皮在拉伸过程中发生移动。并同时约束筋条X方向位移,保证筋条在拉伸过程中不会偏离中心,如图6(a)所示。两根筋条和蒙皮采用C3D8I单元,即8节点六面体单元;R区采用C3D6单元,R区受力复杂,承受应力较大,故适当细化网格。模型网格划分如图6(b)所示。在接触面定义表3所示黏聚接触来模拟蒙皮、筋条和R区接触界面的界面损伤行为。


图6 T型接头三维有限元模型Fig.6 3D finite element model of T-joint

表3 未缝合T型接头界面黏聚接触参数定义
未缝合T型接头有限元计算结果如表4所示。该模型在拉伸载荷下,极限破坏载荷为1 190.20 N, 与试验值相对误差为8.2%。初始失效载荷为940.41 N,与试验值相对误差为5.9%。 误差范围在可接受范围内,有限元模拟结果与实际试验吻合。
图7为未缝合T型接头三维模型模拟计算得到的载荷-位移曲线,在R区出现裂纹之后,即出现第一次掉载,随后裂纹沿着筋条向两边扩散,在载荷达到极限后不再继续增加,直到筋条完全脱离蒙皮。曲线基本形状与试验结果匹配较好,第一次掉载位移都在5~6 mm之间,极限失效载荷也与试验值较吻合。且模型的刚度线性段在试验范围内,说明有限元的建模、边界条件及接触属性比较符合真实情况,基于内聚力模型(CZM)的黏聚接触方法来模拟筋条与蒙皮的脱粘行为具有可行性。
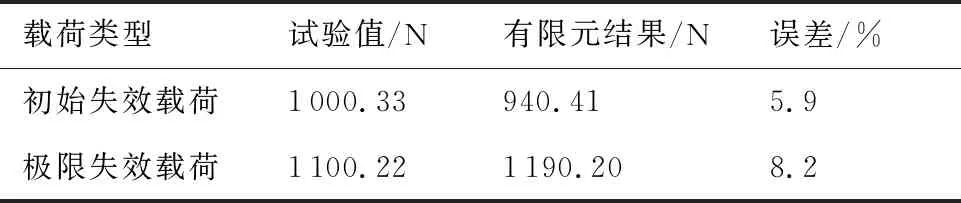
表4 三维模型计算结果Table 4 Calculation results of 3D model
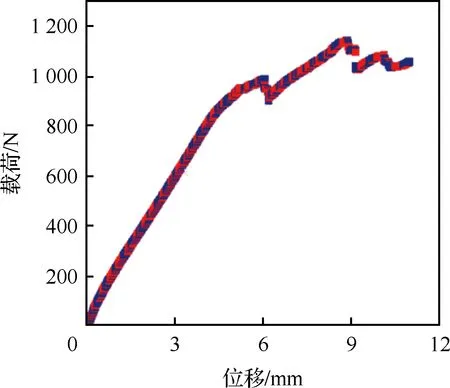
图7 未缝合T型接头模型的载荷-位移曲线Fig.7 Load-displacement curve of unstitched T-joint model
3 缝合T型接头二维模型分析
T型接头三维有限元模型能较好模拟出真实试验情况下T型接头的拉脱性能以及破坏机理。但是三维模型计算量大,模拟时间长,不适合进行参数化分析。为了提高模拟分析效率,尝试简化模型。由于T型接头进行拉伸时,主要是 Ⅰ 型和 Ⅱ 型破坏,Ⅲ 型可以忽略不计[23],因此建立二维有限元模型进行模拟分析,如图8所示。
筋条和蒙皮采用CPE4R单元,即四节点平面应变四边形单元;R区采用CPE3单元。通过在突缘与蒙皮界面相应节点建立非线性弹簧来模拟缝合密度(行距×列距)为10 mm×10 mm的Kevlar-29缝线的增强作用。X方向弹簧模拟界面抗剪切作用,Y方向弹簧模拟界面抗拉脱作用,如图9所示。缝线的桥联律图5已给出。筋条-蒙皮界面参数取为10 mm×10 mm缝合密度的缝合复合材料界面性能,为试验测算而得均匀等效值,见表5。

图8 T型接头二维有限元模型Fig.8 2D finite element model of T-joint
图10所示为缝合T型接头实际拉伸试验与模拟失效云图对比,两者失效形式相似。

图9 非线性弹簧模拟缝线Fig.9 Simulation of thread with non-linear spring

表5 缝合T型接头二维模型界面参数定义Table 5 Interfacial parameters of 2D model of T-joint

图10 拉伸试验与模拟失效云图对比Fig.10 Comparison between tensile test and simulation
图11为有限元模拟得到的缝合T型接头界面失效机制,其中CSDMG表示黏聚接触界面的刚度退化程度,CSDMG值越大表示界面损伤越严重,CSDMG=0表示界面完好无损,CSDMG=1表示界面已完全破坏。有限元结果显示,在拉伸载荷作用下, 损伤首先出现在缘条与R区的界面 (图11(a)),继续加载至结构掉载,缘条与蒙皮间的损伤已大面积扩展(图11(b)),最终破坏时缝线被拉断或拔出,筋条与蒙皮完全分离(图11(c))。缝合不会改变结构的破坏模式,有限元预测的失效机制与试验观察基本一致。

图11 有限元模拟得到的缝合T型接头界面失效机制Fig.11 Interface failure mechanism of stitched T-joint simulated by finite element model
在相同的跨距下,分别对未缝合和缝合二维模型进行有限元拉伸模拟,其中缝合二维模型中分别采用直径400 D、1 000 D和1 500 D的缝线。在有限元中缝线直径体现在非线性弹簧的拉伸强度及桥联律的变化。图12为有限元模拟T型接头拉伸验载荷-位移曲线。
由图12可见,缝合的T型接头的第1次掉载被延后,并且初始失效载荷都高于未缝合模型,这是因为缝合试样中的裂纹扩展受到缝线的阻碍作用,相对于未缝合试样裂纹扩展要缓慢一些。界面裂纹扩展机制如图13所示,在裂纹扩展初期,拉伸载荷线性增长,当载荷增加到一定程度时,裂纹突然扩展,穿越第1排缝线;在裂纹继续向第2排缝线扩展过程中,当第1排缝线形成的桥连区域达到饱合且不足以承受施加的载荷时,第1排部分缝线发生断裂,载荷在此时有一个突降的表现,之后每次载荷突降现象的出现都伴随部分桥连缝线的断裂。与未缝合试样相比,缝合试样载荷波动较为剧烈,桥联区域从出现到饱和,载荷基本保持线性增长,当桥连区域达到饱和,部分缝线断裂,载荷急剧下降,之后又形成新的桥连区域,桥联区域经历“形成-饱和-失效-新桥联区域的形成”这样几个阶段。
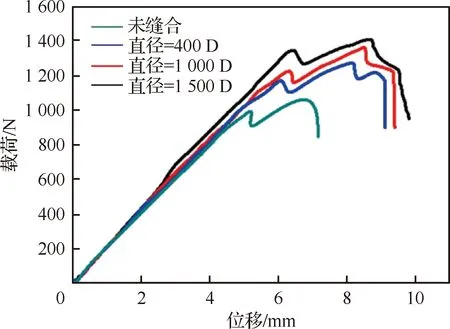
图12 缝合与未缝合T型接头模型载荷-位移曲线Fig.12 Load-displacement curves of stitched and unstitched T-joints
有限元模拟分析结果中,随着缝线直径增加,T型接头拉伸承载力增加,原因是缝线变粗,缝线的桥联力变大,拉伸强度增大,T型接头抵抗拉脱失效的能力提高。值得注意的是,在实际试验中,当缝线直径达到1 500 D时,试样的极限破坏载荷相比1 000 D缝合试样并未提高(表6),原因是有限元模拟分析中未考虑实际情况下缝线可能造成的层合板面内损伤,从而表现为缝线越粗,缝合T型接头的拉伸承载力越高。
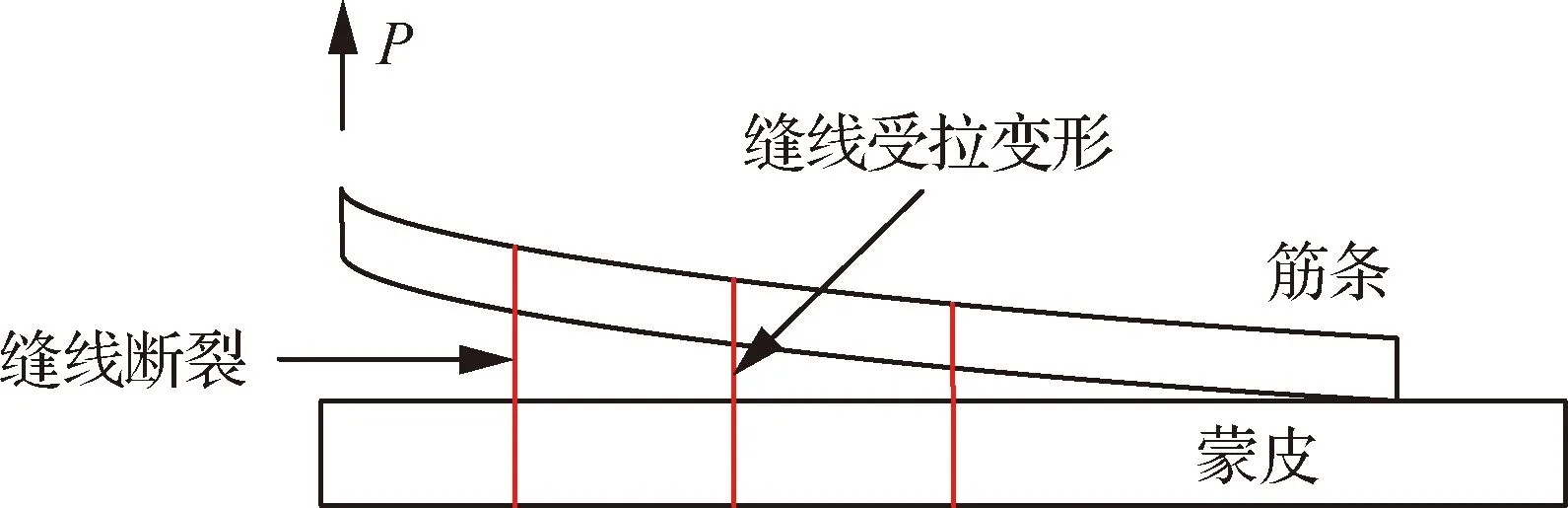
图13 缝合T型接头试样界面脱粘示意图Fig.13 Interface debonding of stitched T-joint sample
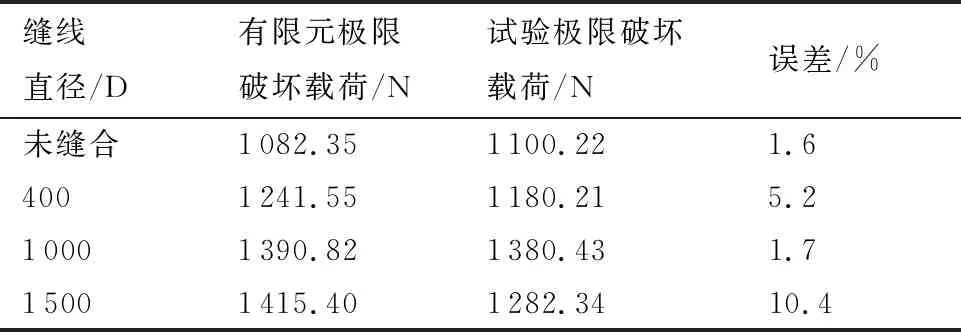
表6 T型接头拉伸承载力模拟值与试验值对比
4 结 论
本文建立了复合材料缝合T型接头的有限元模型,研究了缝合T型接头的界面失效机制及缝合参数对T型接头拉脱承载能力的影响,得出以下结论:
1) T型接头三维模型和二维模型有限元分析结果均和实际试验吻合,验证了分析方法的可行性、合理性。
2) 界面增强不会改变结构的初始破坏位置和最终破坏模式。
3) 缝合能够有效提高T型接头拉伸承载能力。
4) 随缝线直径增大,T型接头极限破坏载荷提高,拉伸承载能力提高。由于模型未考虑缝合对层合板面内性能的影响,忽略了缝线可能造成的材料损伤,当缝线直径增大到1 500 D时,与试验结果存在10.4%的误差。因此,在工程应用中不能一味增加缝线直径和缝合密度,要在达到缝合结构性能目标的基础上最大限度地降低缝合对层合板面内性能的不利影响。
[21] BIANCHI F, KOH T M, ZHANG X, et al. Finite element modelling of z-pinned composite T-joints[J]. Composites Science and Technology, 2012, 73: 48-56.
