基于改进遗传算法的轧机主传动系统参数辨识
2021-03-25张瑞成
张瑞成 李 晨
(华北理工大学 电气工程学院,河北 唐山 063210)
数字孪生的内在发展是让虚拟中的模型不断趋近于现实中的物理模型,以达到在虚拟世界中模拟现实世界的真实情况[3]。在板带轧机的实际生产过程中,轧机主传动系统的数学模型与物理模型之间存在一定的误差,可以通过辨识数学模型的参数来提高系统的模型精度。通过采集实际的数据,拟合实际数据与仿真数据来修正数学模型中的参数使得虚拟越来越趋近于现实,以达到数字孪生的目的。系统参数辨识在1962年被Zadeh[4]所提出:系统参数辨识是指被识别系统按照优化准则在预设模型中优化出与数据拟合最好的模型参数。国内外学者在控制系统的参数辨识中提出了于许多优化算法,例如相关函数法、频率特性法和最小二乘法等。但是这些优化算法在应用过程中逐渐显露出了它们自身的缺点与局限性。最近几十年来,控制算法理论不断成熟发展,产生了多种新型的智能优化算法并且将其运用于参数辨识之中,如遗传算法、人工神经网络与人工蜂群算法等。ERKORKMAZ和KAMALZADEH[5]通过二阶的系统模型,采用实验法修正了系统模型的频响曲线,并且辨识出了质量、阻尼及刚度矩阵等系统参数。ALTINTAS和OKWUDIRE[6]使用二阶系统模型,用最小二乘法辨识出了刚度矩阵、质量及阻尼,成功辨识出了系统质量矩阵的非对角项。张春龙[7]等人采用遗传算法对电静压伺服系统模型进行参数辨识,并对系统的模型参数进行了优化,提高了系统的模型精度。
针对传统遗传算法在轧机主传动系统参数辨识中具有早熟和收敛速度较慢等缺点,运用了改进的遗传算法来辨识轧机主传动系统中的参数[8]。将算法中的交叉算子与变异算子的操作以及自适应交叉概率和变异概率应用于系统参数辨识中。改进之后的算法可以让群体中最大适应度的个体避免陷入变异率和交叉率为零的状态,从而使得优良的个体可以始终保持在交叉与变异的状态从而让轧机主传动系统参数辨识避免出现局部最优的问题并且提高了辨识速度。辨识结果表明,该算法相较于传统的遗传算法来说优化速度更快和具有更高参数优化精度,证明了改进算法的有效性。
1 轧机主传动系统模型
我们可以适当的简化一下轧机主传动系统,把它当成轧辊与电机通过弹性轴连到一起的两惯性质量—弹簧质量系统。且有许多的非线性因素影响轧机运行的,例如间隙、接轴倾角、轧制扰动、时滞、非线性刚度和非线性阻尼等,最终选择非线性阻尼和非线性刚度,因为这两个因素在二质量系统中比较具有代表性,按照上述所言建立系统模型[9]。
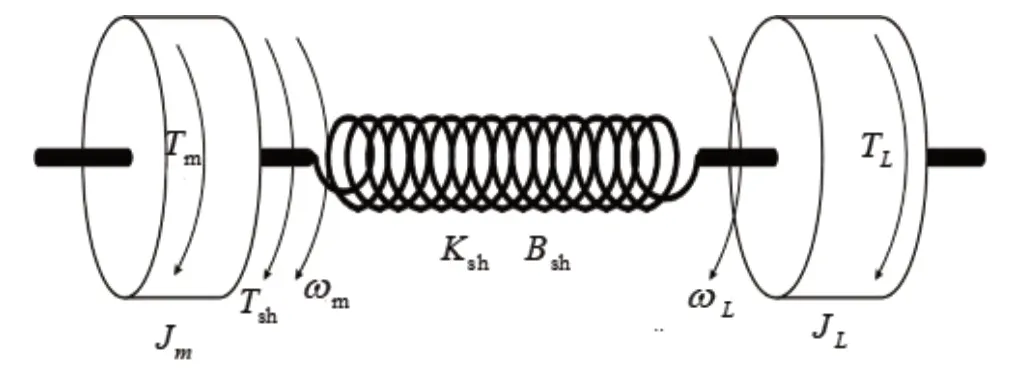
图1 板带轧机主传动系统模型图
ωm为电机端角速度;ωL为负载端角速度;TL为负载阻力矩;Tsh为弹性轴扭转力矩;Jm和JL分别为电机端和负载端的转动惯量;Tm为电机力矩。Ksh为准周期刚度系数,Bsh为非线性阻尼,其表达式为:

式中:α为轧辊与扎件之间的相对滑动速度系数。
根据物理连接特性可以推出系统的微分方程:
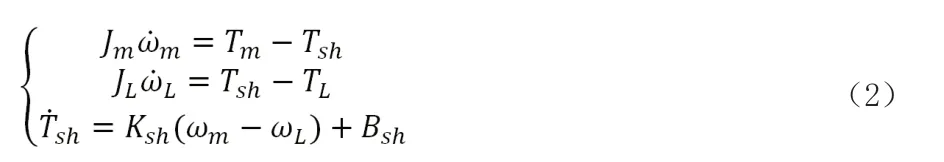
根据现代控制理论,可以写出系统的传递函数为:
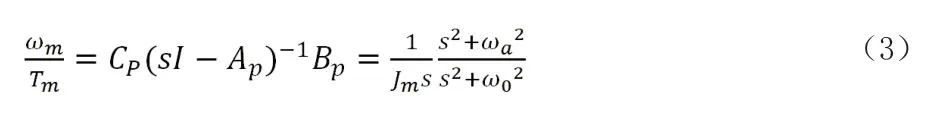
蔬菜苗期常见的主要病害有猝倒病、立枯病,此外还有瓜类枯萎病、番茄早疫病、灰霉病以及沤根、根腐病等;常见的主要虫害有蛴螬、蚜虫、蝼蛄、白粉虱等。苗期病虫害也很难达到预期的防治目的,因此,为了尽可能地少施或不施农药而培育出优质稳产的无公害蔬菜壮苗,就必须采取以预防为主的综合防治措施。
2 基于改进遗传算法的系统参数辨识
2.1 编码
要得到系统的每个时刻的输出值,需要将传递函数离散化。通过辨识模型中的参数Ksh和α,可以得到b0,b1和a1从而得到系统的辨识输出值。从轧机主传动系统的实际情况出发,对染色体采用二进制的方式来编码。
2.2 产生初始种群
采用小区间生成法来产生初始种群,将Ksh和按照其取值范围平均分为若干个小区间,区间总数为种群总数。并在每个小区间内随机的产生一个个体,最后将每个小区间产生的个体组合起来列为初始种群。根据现实实际经验,将Ksh的取值范围设为[5×106,7×106],α取值范围设为[0,1]。小区间生成法产生的初始种群,个体会均匀地分布在整个设立的取值范围之内,而且能确保初始个体之间存在着明显的差异,从而使初始种群能够包含更多的信息,提高了算法最终收敛于全局最优解的概率。
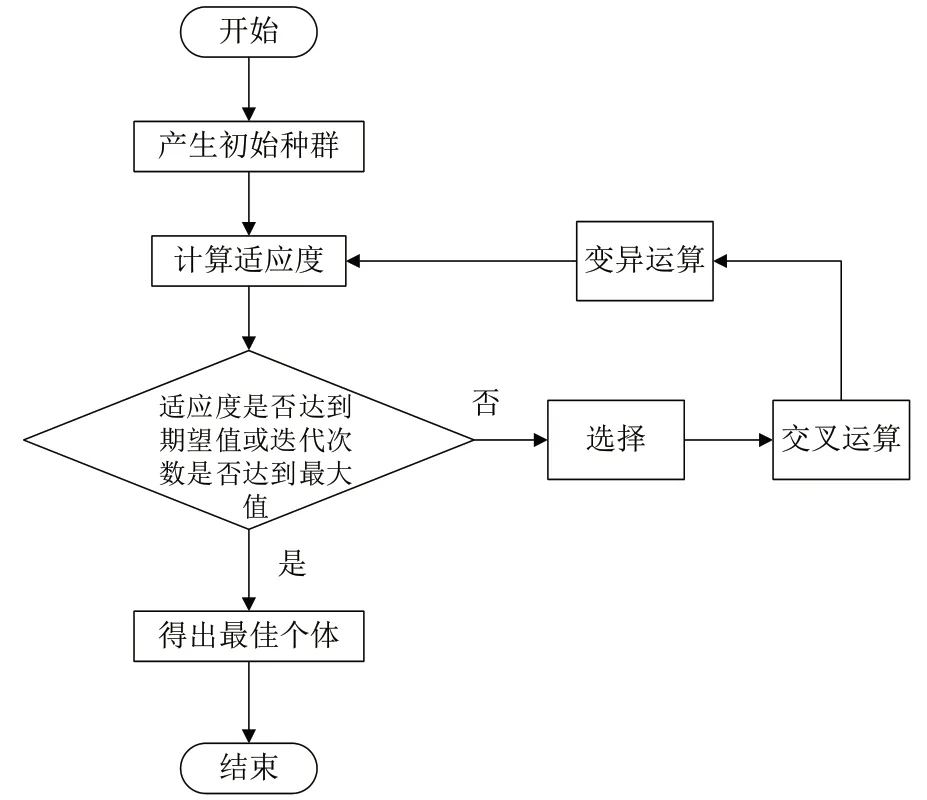
图2 遗传算法流程图
2.3 构造适应度函数
根据轧机主传动系统的实际情况来构造适应度函数,利用每一个T时刻实际输出与模型输出的差值的平方和的倒数来表示适应度 函数。

式中,y′为相同输入下辨识模型的输出;n为采样点的个数;y为实际对象的输出。
2.4 选择操作
轧机主传动系统在应用传统遗传算法时候,变异概率pm和交叉概率pc可能在一些特定的情况下变得很大,从而会使得适应力较好的个体产生变化。所以在改进遗传算法中选择操作中采用精英保留策略来存留种群中的精英个体,精英个体指的是适应度更高的个体。具体操作是将父代中种群最高适应值的个体和每次进行遗传算法后的子代中种群最高适应值作对比,如果父代种群中的最高适应值大于子代的适应值,就从子代种群中随机移除一个个体,并往子代种群中加入父代种群中最高适应值的个体形成新一代的种群。精英保留策略可以让种群之中最优秀的个体不会被变异、交叉等遗传运算改变,保证了改进之后遗传算法的收敛性。
2.5 种群的变异与交叉
变异和交叉运算在轧机主传动系统参数辨识中的性能起了关键的影响。影响交叉和变异运算的主要是取决于如何改变交叉概率pc和变异概率pm。如果交叉概率pc过小,会让搜寻的过程变得缓慢。pc越大,新个体生成的速度就越快,但是当pc过大时遗传中个体被改变的可能性就会越大;对于变异概率pm来说,如果取值过大,遗传算法就会成因为随机性过大从而变成随机搜索算法。如果取值过小,种群就不容易生成新的个体[10]。
对于不同的优化对象,需要进行反复的实验来寻找最合适的pc与pm。为此,Srinvivas等人提出来了一种自适应遗传算法[11]。pc和pm能根据具体情况自行变化。当种群中个体适应值比较分散时,pc和pm减小;当种群个体适应值趋近于局部最优时,pc和pm增大。因此,自适应遗传算法中的pc和pm能提供对于具体问题的最佳pc和pm。而且为了避免算法在运算初期陷入局部最优解,把种群之中适应值最大个体的交叉概率pc和变异概率pm分别增加至某一非零值pc2和pm2,变相地增加了种群当中优良个体的变异概率和交叉概率,让算法不会一直处于停滞不前的状态,让算法以更快的速度不断逼近全局最优解。改进之后的交叉概率pc和变异概率pm的计算表达式为[10]:

式中,pc1,pc2,pm1,pm2均为(0,1)区间上的参数;favg为每代种群的平均适应值;fmax为种群中的最大适应值;f为要变异个体的适应值;f′为要交叉双方适应值较大者的适应值。
3 仿真分析
运用MATLAB编写程序进行仿真。采取某厂2030mm带钢冷连轧机第4机架实际参数建立板带轧机主传动系统模型进行仿真研究。辨识算法参数如表1所示:

表1 辨识算法参数
为验证改进算法的性能,将其与和传统遗传算法进行对比实验。将Ksh的取值范围设为[5×106,7×106],α取值范围设为[0,1]。独立运行20次,并记录其平均值。

表2 传递函数模型辨识结果对比表
在表2中,改进之后的遗传算法对参数α的辨识误差率在2.4%左右,相比于传统遗传算法的4.36%误差率降低了1.96%。对于参数Ksh的辨识,改进遗传算法误差率为0.0425%,传统遗传算法误差率接近0.15%,误差率减少了2.83倍。这表明改进的自适应交叉变异操作和精确保留策略可以有效地提高参数辨识精度。反映了改进之后的遗传算法对系统参数辨识的良好全局搜索能力并且实现更快地收敛到最佳状态。
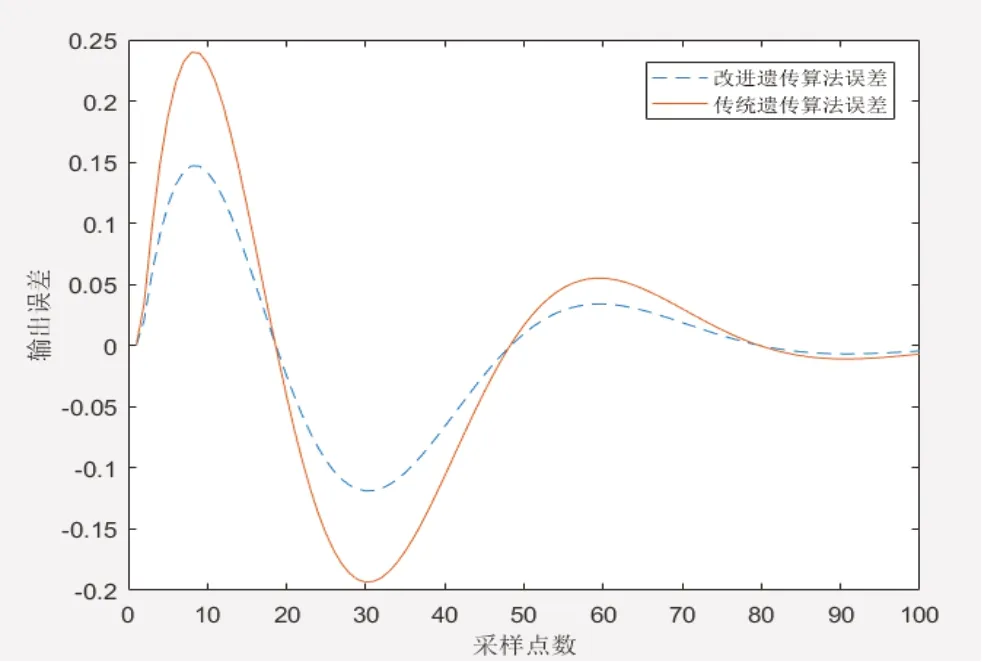
图3 辨识结果误差
图3为分别为采用传统遗传算法和改进遗传算法的转速误差曲线。由图可知,改进之后的遗传算法输出误差在-0.1至0.15之间,传统遗传算法输出误差在-0.2至0.25之间。改进之后的遗传算法相比传统遗传算法每一时刻的输出误差更小,且具有更高的辨识精度,通过辨识程序得到的参数较优,可以获得很好的优化效果。
4 结语
采用改进遗传算法并将其运用于的参数辨识之中。
1)改进后的遗传算法在轧机主传动系统中相较于传统遗传算法在辨识参数误差率和收敛速度都有比较大的提高。
2)改进后的遗传算法可以适用于非线性系统的参数辨识之中,这为解决非线性系统的参数辨识提供了一条有效道路。
3)通过参数辨识提高了轧机主传动系统数学模型的精度使其越来越趋近于现实物理模型。为接下来进一步研究轧机主传动数字孪生系统提供了理论和实验基础。
