基于多目标多约束的生产制造业的计划排产问题研究
2021-03-25解云龙袁鲁平朱宁帅
解云龙,袁鲁平,朱宁帅
(山东联诚精密制造股份有限公司,济宁272100)
随着市场竞争的加剧,保证交期是生产制造业生产制造过程中的核心竞争力之一。中国很多生产制造企业开始转向按订单生产(MTO),甚至按订单设计(ETO)的制造模式[1-2],这种情况下,通过计划排程控制产品最终的交期,变得越发重要。保证产品最终交期,在生产制造过程中体现为最小化生产完成时间。最小化生产完成时间基本上涉及两个目标,即最小化机器闲置时间和最小化订单提前率/延迟率。必须通过考虑所有约束条件(例如优先级、可用机器、机器转换、机器设置、机器容量、大量库存等)来实现这两个目标的最小化。这需要通过高级计划和排程(APS)来实现。APS 本质是实现有限资源的优化配置和调度,需要依靠强大的计划和排程算法驱动,很多学者在这些方面做了大量的研究。文献[3]给出了基于常规遗传算法和基于混合遗传算法的车间作业调度问题的有效解法,文中表明混合遗传算法在比常规遗传算法效果更好,在更短的时间内找到最佳结果;文献[4]和文献[5]提出的基于多阶段的多目标遗传算法(moGA)可以有效求解生产车间计划调度(JSP)过程中多目标多约束的问题,并引出惩罚系数解决遗传算法陷入局部最优解的问题;文献[6]和文献[7]解释了自适应遗传算法的概念,该算法以最佳适应性自适应地生成染色体,实现了在n 个工序(job)的m 台设备/工作中心(machine)上进行计划调度,该过程是一个典型的NP-Hard 问题,求解及其复杂。因此,为了解决这个问题,给出了一种具有基于禁忌搜索的遗传算法,即GATS[8]。GATS 的主要方法是最小化制造时间、处理时间和迭代次数,从而获得更好的结果[9-10]。文献[11]针对多目标高级计划和调度问题的基于偏好的自适应遗传算法研究中心中给出了数值实验,以说明所开发算法的有效性和效率。
综上所述,本文提出了一种基于迭代搜索技术的遗传算法,以实现生产制造生产车间的多目标多约束条件下的计划调度问题。本算法采用通用编程模型的形式,可以满足所有优先级和替代机器容量的限制。基于迭代搜索技术的遗传算法主要考虑3个步骤,即染色体编码、确定适应度函数以及将遗传算子用作选择、交叉和变异3 个步骤,以最小化目标函数并提供更优化的解决方案。
1 车间调度模型
本节描述了典型的装配车间生产计划和排产数学模型,该模型已经在大多数研究中应用[3-7]。
车间调度数学模型的变量列举如下:
K:订单数量
D:位置数量
N:资源数量
Ok:订单K 一组工序
JK:订单K 的工序数
Mm:第M 项资源
Pd:第d 处位置
qk:订单K 的批量
Am:在Mm上资源加工的工序
Pkim:机器m 上的Oki操作的单位处理时间
Lm:设备m 上的产能
tkilj:从Oki操作到Okj操作的设置时间
tmn:设备m 到设备n 之间的单位运输时间
ukij:从运行Oki到运行的订单k 的单位负载大小
Sd:工厂Pd的资源集
Ld:可用于从Pd运输的资源集
rkij:优先约束

考虑到每台机器上每个工序的处理时间的输入数据集,每个工序之间的建立时间和每台机器之间的转换时间,优化两个目标函数所需的各种参数如下:
(1)加工工时

(2)订单k 的完工时间
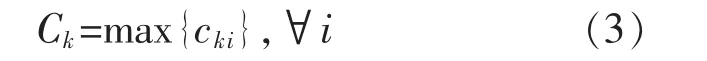
(3)从机器m 到机器n 的总运输时间

(4)设备M 的工作负荷
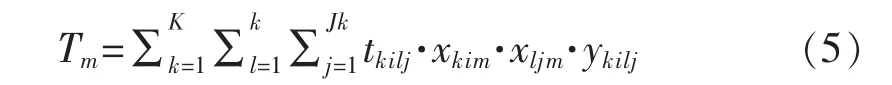
(5)设备总空闲时间

式中:i,j 为工序号序列,i,j=1,2,…,Jk;k,l 为订单号序列,k,l=1,2,…,K;m,n 为资源号序列,m,n=1,2,…,N;d,e 为位置号序列,d,e=1,2,…,D。
在每个方程式中,变量xkim,ykilj称为决策变量,可以通过将条件循环应用为以下变量来应用:


目标函数

这两个目标函数必须通过牢记一些约束来最小化:
(1)如果出现以下情况,机器不能同时处理多个操作

(2)在以下情况下,确保机器之间的中间传递:

必须满足以上两个约束条件,这样操作才能在一台机器上运行而不会产生任何中断。
(3)产能约束条件满足:
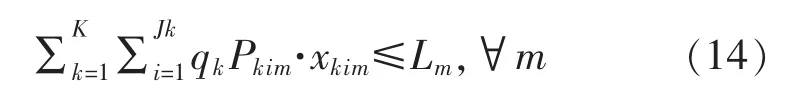
(4)如果没有违反关于优先级限制的保证:
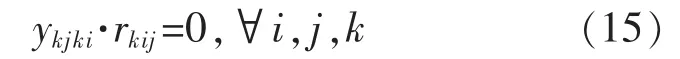
(5)确保灵活的工序(操作顺序):
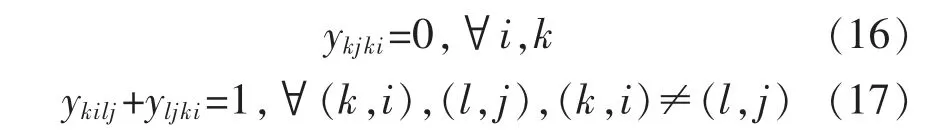
(6)对可变的设备列表选择:
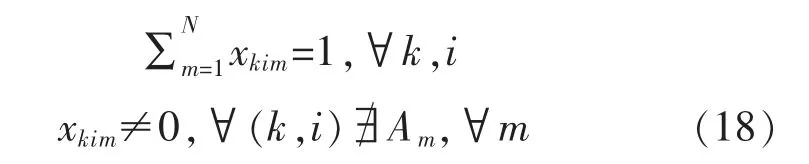
2 计划排产问题
2.1 用例描述
基于上述的数学模型建立车间计划排产问题的数学解法,将问题定义为(订单数量,工序数量,资源数量)。采用经典的数据模型[3-4](2,10,4),(4,17,6),(5,25,8),(8,40,10),(20,70,15)(30,150,20)。对于所有这些要满足的问题,参数和约束需要设置3 个输入数据集,即在各种资源上的每个工序的处理时间,每个工序之间的设置时间以及资源之间的转换时间。其中表1 是对应工序在对应设备/工作中心的加工时间;表2 为不同设备之间的转移时间;表3 为不同工序之间的设置时间(前置时间)。
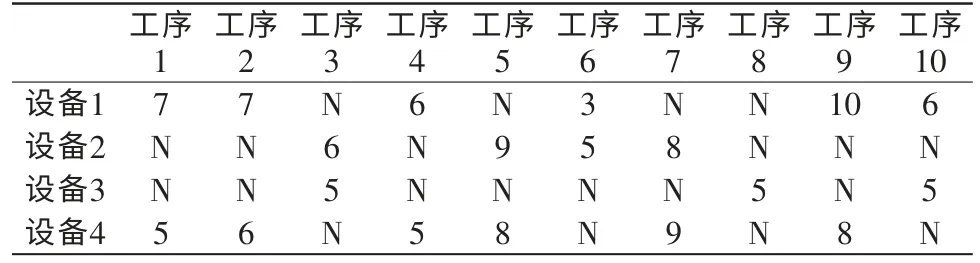
表1 对应工序在对应设备/工作中心的加工时间/(min)Tab.1 Processing time of corresponding process in corresponding equipment/work/(min)
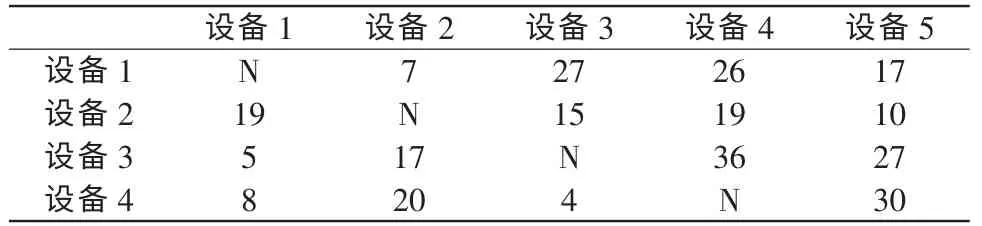
表2 不同设备之间的转移时间/(min)Tab.2 Transfer time between machines/(min )
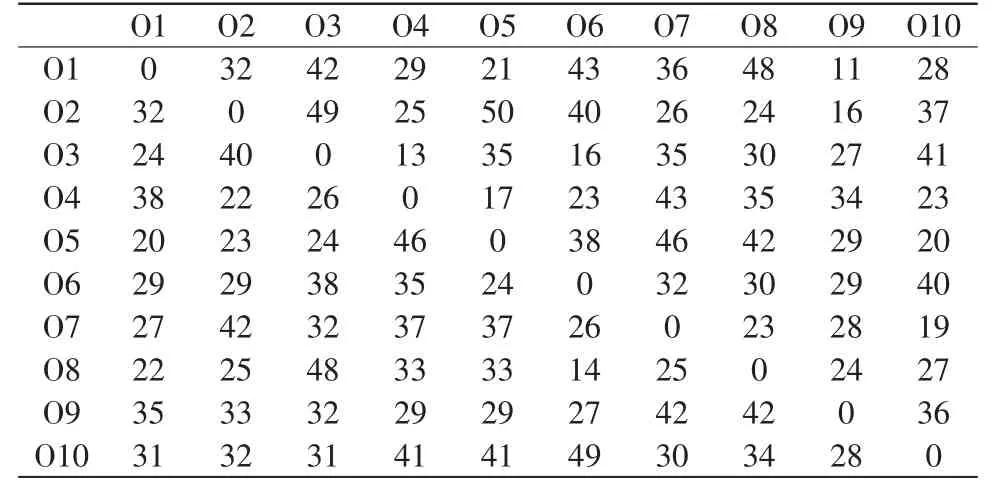
表3 不同任务的安装时间/(min)Tab.3 Setup time of different tasks/(min)
对于数据(2、10、4),所有10 个操作都可以在多台机器上处理,因此称为自由工序。
2.2 基于迭代搜索技术的遗传算法优化
可以通过最小化上述两个目标函数f1和f2来找到给定过程的最优解。相对于给定数据集和约束条件,可以通过应用遗传算法的概念来最小化这两个方程。遗传算法会为给定问题生成随机解的数量,并从中选择适合度最大的一个。这些解决方案将进行多次迭代以找到最大拟合值。具有最大适合度值的解决方案表示最佳解决方案。在遗传算法应用可以通过考虑设置一些基本参数:
最大变种数MG=100;
种群规模Psize=50;
最大迭代数N=50;
目标函数Oj1的权重w1=0.2;
目标函数Oj2的权重w2=0.5;
最早时间的权重α=0.1;
总延迟时间的权重β=0.9;
2.2.1 工序优先级分配向量
这基本上是通过牢记优先约束来随机处理所有工序的分配,以完成所有任务。由于在上述案例研究中有10 个工序。这意味着为机器生成的初始染色体只会随机生成10 个带有随机序列的操作的染色体。用P1表示。
如图1所示,从P1到Pn随机生成工序分配矢量的数量,其中n 表示总代数。
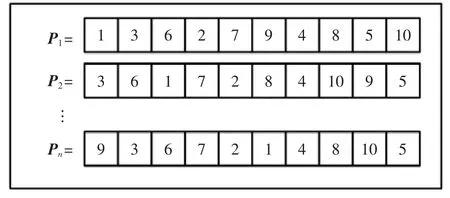
图1 遗传算法中工序优先级分配向量示图Fig.1 Vector diagram of process priority allocation in genetic algorithm
2.2.2 工序的设备分配向量
再次为上述工序随机分配设备/工作中心。由于针对提供的不同设备进行处理时,每个工序都具有不同的加工时间,因此设备分配是寻找遗传算法最优解的有效任务之一,对于每个工序序列,将分配多个设备序列,即从M1到Mn,如图2所示。

图2 遗传算法中工序的设备分配向量示图Fig.2 Vector diagram of equipment allocation in genetic algorithm
(1)适应度函数
最佳解决方案是由对前代具有更高适应性的染色体代表的,公式如下:

式中:w1和w2是基于目标函数的分配权重。
(2)交叉
通过保持对应工序的设备分配向量相同,可以选择具有最高适应性的2 条最佳染色体,示意图如图3所示。
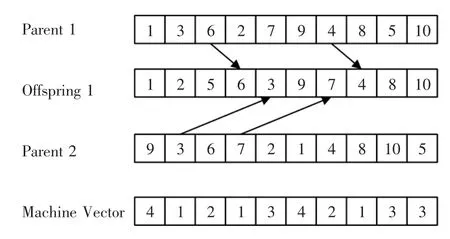
图3 遗传算法中交叉过程示图Fig.3 Diagram of crossover process in genetic algorithm
(3)突变
遗传算法中突变的实际目是检查在杂交过程中产生的后代具有比先前最大适应性的其他可能性。在计划排产问题上表现为从每个工序处理时间的给定数据来看,每个工序在不同的机器上具有不同的执行时间,如图4所示。
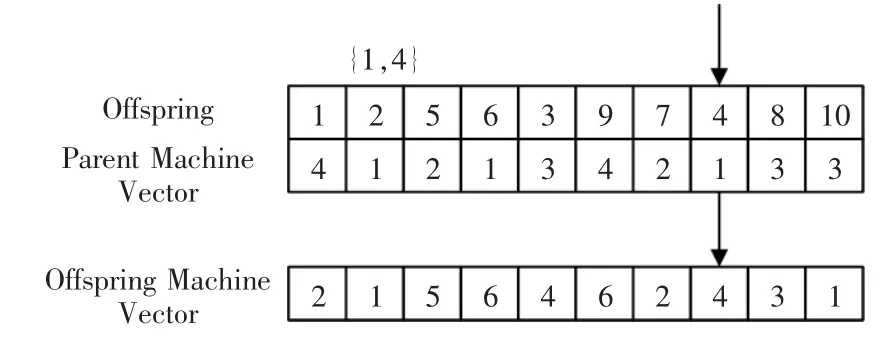
图4 遗传算法中突变过程示图Fig.4 Diagram of mutation process in genetic algorithm
3 结果与讨论
表1 中显示了针对每台设备的优化测试计划。它由行数为1~4 的行的矩阵组成,每台设备的工序顺序为1~10。优化的时间表显示,首先为所有4 台设备选择了所有独立的操作。其余工序将得到优先处理。
对于用例(2,10,4)采用上述基于迭代搜索的遗传算法的优化。得到优化结果如表4所示,图5展示了当前适应度函数的设备利用率。
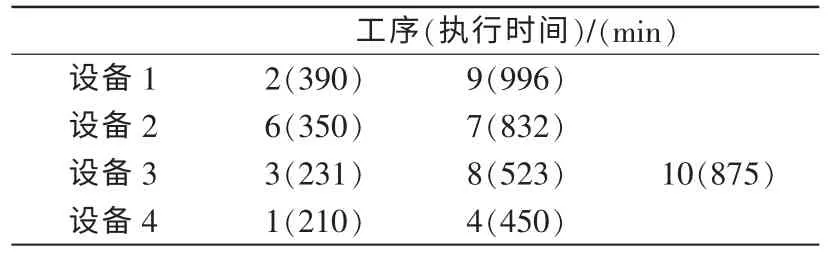
表4 对于(2,10,4)的优化结果Tab.4 Optimization results of(2,10,4)
与以往的研究对比发现[3-5],在相同的目标函数下,优化结果更佳,且计算时间更短。
迭代次数在最小化编译时间的情况下起着至关重要的作用,可以最大程度地减少总生产时间,确保交期,表5 给出了几个数据集下的最小化完工时间。
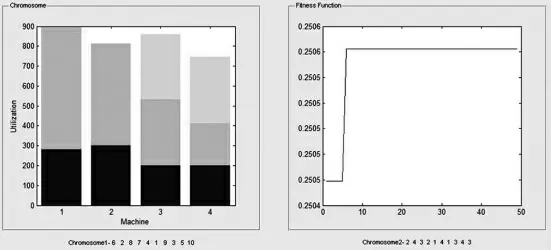
图5 设备利用率Fig.5 Equipment utilization

表5 迭代搜索遗传算法下的最小化完工时间Tab.5 Minimizing completion time under iterative search genetic algorithm
4 结语
本文给出了一种迭代搜素的遗传算法(IGA),该算法提供引入了均值汇编参数,建立基于一个编程模型的遗传算法,可以在满足多约束条件的情况下最小化生产的总生产时间,经与以往研究对比发现,该算法可行。同时针对不同的数据集进行计算分析,这些数据集的求解结果与迭代次数的所需变化有关。因此,对于多目标多约束高级计划和调度,基于迭代搜索的遗传算法可以以较少的计算时间找到给定问题的最佳和最佳解决方案,可以满足实际生产应用中的实时性要求,尤其是在以按订单设计(ETO)、按订单生产(MTO)制造模式为主的生产制造业具备良好的应用性。
