基于神经网络的配变无功补偿装置故障远程监测方法研究

黄 宇，欧家祥，李航峰，张俊玮，沈兴富

（1.贵州电网有限责任公司电力科学研究院，贵阳550002；2.贵州黔驰信息股份有限公司，贵阳550002）

目前用电负荷不断增加，利用无功补偿装置调节电网电压可避免电压低于或高于临界电压。但无功补偿装置的工作故障率较高，影响用户用电及供电局服务水平。因此需深入研究补偿装置故障远程监测方法，及时诊断装置故障[1]。

国内装置故障远程监测技术已取得较大发展，将信号处理技术应用到故障监测中，分析补偿装置故障对电网电路幅值包络的影响，获取故障信号感应规律，利用广义变换的方法，诊断补偿装置的补偿电容，提取装置通信信号时频信息，检验时频信息的频率变化，对故障电容的位置进行定位，实现故障状态的远程监测[2]。

在以上理论的基础上，本文提出基于神经网络的配变无功补偿装置故障远程监测方法。神经网络利用分布式并行信息处理方式，调整补偿装置内部节点的连接关系，分析装置故障。

1 基于神经网络的配变无功补偿装置故障远程监测方法

1.1 采集配变无功补偿装置状态信息

采集配变无功补偿装置通信信号，获取补偿装置的运行状态信息。设置监测主站和采集终端，相互交换补偿装置的状态数据，采集终端使用三层B/S结构，利用具有复杂逻辑操作的C/S 模式，将多种类型的通讯设备，连接到补偿装置[3]。采集终端的通信接口采用RS-485 芯片，通过光电隔离芯片和数字电路，在RS-485 主控电路中添加压敏电阻和气体放电管，以此增加无功补偿装置静电放电的抗性，再利用变压器、隔离电源回路、通信回路、以及RS-485主控电路，为RS-485 电路单独供电[4-5]。采取拨号形式，将监测主站的服务器接入Internet，通过中压电力线载波这一通信信道，接收采集终端的传输信号[6]。此时补偿装置的采集信号可表示为

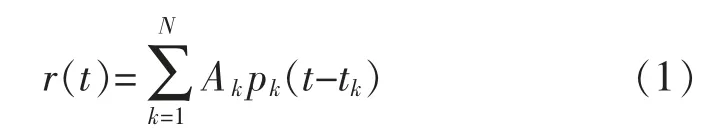
式中：r（t）为t 时刻，监测主站采集的补偿装置通信信号；k 为采集信号的多径数目；N 为多径数目的总数量；Ak为第k 条多径的幅度；tk为第k 条多径的时延；pk为第k 条多径的衰减信号波形[7]。消除采集信号的干扰信号，使用自适应数字滤波器，通过参数可调的方式，对采集信号进行滤波处理，转换为数字信号。对比数字信号和期望信号，得到误差信号，通过自适应干扰消除算法，更新调整滤波器参数，输出干扰程度达到最小的采集信号[8]。假设期望信号与输入信号为联合平稳过程，则自适应滤波算法为

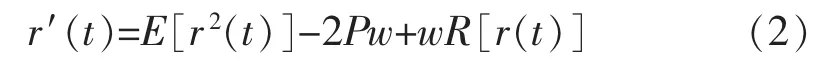
式中：E 为主通道输入信号r（t）的方差；R 为r（t）迭代运算的更新量大小；w 为滤波器最优权值矢量；r′（t）为滤波器t 时刻的输出信号；P 为r（t）的自相关系数[9-10]。

1.2 监测无功补偿装置运行参数

利用传感技术，融合处理补偿装置状态信息，降低采集数据的虚警率和信息熵，在信息状态量之间建立联系，提高信息状态量的有序度，对装置运行状态进行一致性描述，以此识别装置无功补偿参数。获取补偿装置运行状态的有功功率P，公式为

式中：T 为补偿装置监测周期；u（t）为t 时刻补偿装置的瞬时电压；i（t）为瞬时电流[11]。补偿装置的无功补偿量Q 为

式中：cosφ1为装置补偿前功率参数；cosφ2为补偿后功率参数，数值介于0～1 之间[12]。补偿容量应满足的不等式为

式中：P1为最大负荷日平均有功功率；P2为最大负荷日平均无功功率；φ3为采用大负荷日平均功率因数[13]。

监测补偿装置的供电线路，比较额定电压与节点实际电压，计算电压偏差百分数ε：

式中：U1为节点实际电压有效值；U2为该供电线节点，对应标称电压有效值[14]。利用ε 确定节点实际电压与理论值的偏离程度，当偏离程度超过1%时，判断补偿装置供电电压产生偏离。记录电压偏离的越限时间，计算该时间与监测周期的比值，得到补偿装置电压不合格率，设置不合格率的最高限值为2%。测量监测周期内的电压幅值，计算补偿装置的电压波动率d：

式中：W1、W2分别为监测周期内电压幅值的最大值和最小值；W3为补偿装置额定电压幅值，设置电压波动率的最高限值为1%。采用三相电量法，计算补偿装置的三相电压不平衡度。电压不平衡度算子L公式为

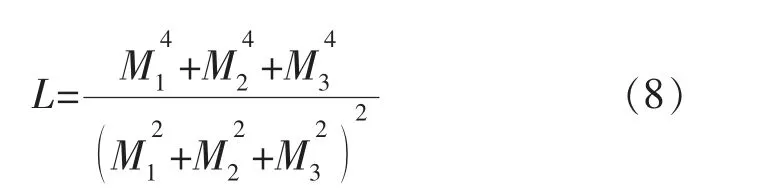
式中：M1、M2、M3分别为三相线电压有效值[15]。补偿装置的三相不平衡度δ 为

设置三相不平衡度的最高限值为2%。最后监测补偿装置的动态响应时间，过程如图1所示。

图1 装置动态响应时间示意图Fig.1 Schematic diagram of dynamic response time of the device

如图1所示，发出控制信号后，装置响应时间应达到无功输出值90%的所用时间，且没有产生过冲。实时监测补偿装置的电能质量数据，对无功补偿容量、电压偏差、电压波动率、三相不平衡度、装置响应时间进行评估，至此完成无功补偿装置运行参数的监测。

1.3 基于神经网络识别无功补偿装置故障类型

当监测参数产生异常变化时，判断无功补偿装置发生故障，对故障类型进行识别，实时跟踪故障参数的变化情况，得到故障样本，传送到监测主站，利用神经网络的人工智能算法，对无功补偿装置故障进行编号分类。通过采集终端，采集装置运行状态的振动信号，针对预处理后的信号，进行小波分解系数单支重构，将振动信号各个频段的谱峰能量值，作为补偿装置的故障特征量，从而获取故障信号数值描述的特征信息，得到神经网络输入的训练样本。再利用模糊关系矩阵和模糊规则，描述振动信号与故障原因、故障种类之间的关系，得到补偿装置的主要故障类型，将其作为神经网络的检验样本。确定神经网络结构，初始化各层接点数量，得到隐藏层和输出层的输出值，调整输入层至隐藏层的连接权值，以及隐藏层和输出层的输出阈值，计算实际输出值与训练样本的偏差。多次更新训练次数，减小输出值与训练样本的误差，实现装置故障特征的神经网络训练，将输出值与检验样本进行对比，识别无功补偿装置的故障类型。记录故障类型和故障时刻，判断装置产生故障的原因，实现基于神经网络，无功补偿装置故障类型的识别。至此完成基于神经网络的配变无功补偿装置故障远程监测方法设计。

2 实验论证分析

进行对比实验，将此次设计方法记为实验A组，两种传统无功补偿装置故障远程监测方法，分别记为实验B 组和实验C 组，比较三组实验识别补偿装置故障的准确率。

2.1 实验准备

以某供电局为实验对象，统计时段为10月1日～10月15日，选取一条典型的10 kV 配电线路的补偿点进行无功补偿，具体参数如表1所示。

表1 实验参数设置Tab.1 Experimental parameter setting

利用无功补偿装置，在补偿点投入相应补偿容量，此时配电线路的各点电压如图2所示。

图2 电网线路无功补偿前后电压Fig.2 Voltage before and after reactive power compensation

三组实验分别对补偿装置的运行状态进行监测。实验A 组对无功补偿装置的常见故障进行数字化归类，划分为正常状况和11 种故障状况，如表2所示。

在表2所示的每种状态中，获取20 组样本，将前10 组作为神经网络的训练样本，后10 组作为检验样本。提取装置运行时产生的信号，处理后提取信号特征，得到神经网络训练的输入值。设故障信号的误差能量为E，此时神经网络输出值与训练样本和检验样本的对比结果如表3所示。

表2 无功补偿装置正常状态及常见故障类型Tab.2 Normal state and common fault types of reactive power compensation device

表3 神经网络实际输出值对比结果Tab.3 Comparison results of actual output values of neural network

如表3所示，训练样本和检验样本与实际输出值的误差能量值较小，最大误差能量为2.81E，说明训练样本和检验样本与实际输出值之间较为吻合，因此实验A 组将神经网络输入端节点数量定为10，对应无功补偿装置的运行状况，以此实现故障监测具有合理性。

2.2 实验结果

2.2.1 第一组实验结果

三组实验采集无功补偿装置的运行状态信号，设置采样频率为50 kHz，信号时速为30 km/h，实际采集的补偿装置信号频谱，在2500 Hz 发生明显频率畸变。在此基础上，利用单边衰减脉冲信号模型，仿真装置故障信号，设置故障频率为2500 Hz，三组实验采集并处理信号后，比较异常信号的中心频率，实验结果如表4所示。

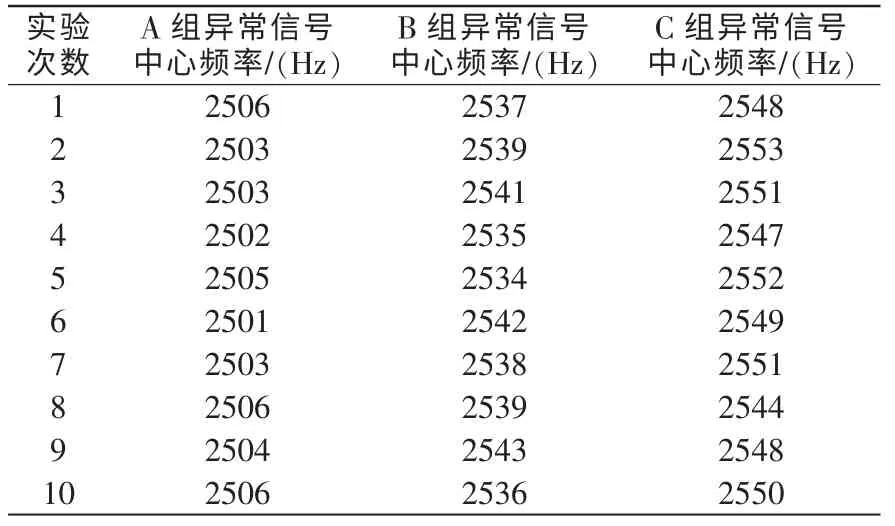
表4 第一组实验结果Tab.4 Experimental results of the first group

如表4所示，实验A 组异常信号的平均中心频率为2504 Hz，实验B 组和C 组的平均中心频率分别为2538 Hz、2549 Hz，A 组与2500 Hz 更加接近。2.2.2 第二组实验结果

在第一组实验的基础上，改变占空比，检验三组实验提取的故障信号，与无功补偿装置故障仿真信号的相似程度。利用互相关系数，衡量故障信号的提取效果，相关系数越大，提取信号与原信号越相似，实验对比结果如表5所示。

表5 第二组实验结果Tab.5 Experimental results of the second group

如表5所示，当占相比增加时，提取信息的相关系数也随之增加，但实验A 组相关系数一直高于B 组和C 组，平均相关系数为0.850，B 组和C 组平均相关系数分别为0.783、0.736，A 组相关系数分别提高了0.067、0.112。

2.2.3 第三组实验结果

三组实验提取故障信号特征信息后，识别无功补偿装置的故障类型，利用Matlab2010b 软件平台，统计三组实验对不同故障状态的诊断结果，计算故障诊断准确率，结果如表6所示。

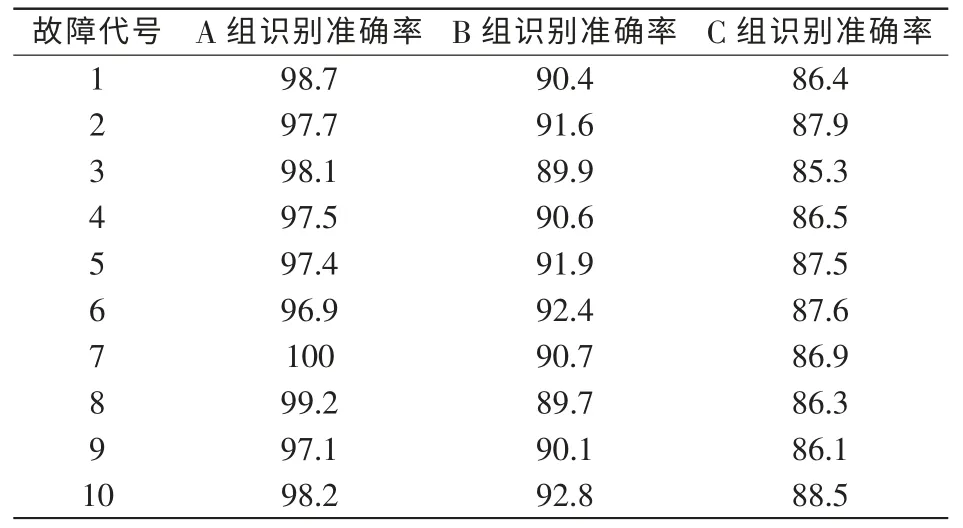
表6 第三组实验结果Tab.6 Results of the third group

如表6所示，针对无功补偿装置的常见故障类型，实验A 组平均识别准确率为98.1%，实验B 组和C 组识别准确率分别为91.0%、86.9%，A 组识别准确率分别提高了7.1%、11.2%。

综上所述，此次设计方法相比传统方法，减少了故障信号采集频偏，提高了故障信号提取效果，采集异常信号的中心频率更接近实际故障频率，与实际故障信号更加相似，在此基础上提取故障信号特征量，利用神经网络识别故障，提高了无功补偿装置故障类型的识别准确率。

3 结语

此次设计方法利用神经网络，对补偿装置故障进行识别，提高了故障诊断准确率。但此次方法仍存在一定不足，故障参数监测局限于稳态评估，在今后的研究中，会对比无功补偿装置的补偿性能，实现暂态部分的电能质量分析。