小型民用飞机颤振试飞数据处理研究

寇宝智，卢晓东

（中国飞行试验研究院飞机所，陕西 西安710089）

关于小型民用飞机的颤振适航验证问题，中国、美国和欧洲等国家和地区都在适航规章中都有明确的相关要求，即所有新设计型号或对颤振特性有重要影响的重大改进型号，都必须通过理论分析、地面试验、颤振飞行试验或其他必要的手段，表明飞机在气动弹性稳定性要求的包线内都不发生颤振。中国适航规章CCAR23部《正常类、实用类、特技类和通勤类飞机适航规定》在23.629“颤振”条款中给出了颤振适航验证的相关要求，通过条款要求可知飞行颤振试验是必须的符合性验证方法。CCAR23.629（b）条规定必须用飞行颤振试验表明飞机没有颤振、操纵反效和发散，并表明在直至VD的速度范围内采取了合适的和足够的步骤来激发颤振，试验中结构的振动响应表明不发生颤振，在速度VD时阻尼有合适的余量，接近VD时阻尼没有大而迅速的衰减。由此可见，在小型民用飞机颤振试飞中，关键模态的阻尼辨识是试飞数据处理中的关键技术，阻尼辨识关系到飞机试飞效率与安全。

目前颤振飞行试验工程实用的阻尼辨识算法很多，主要依据所采用的结构激励手段选择。对于借助电传类飞机飞控系统的操纵面激励[1-2]与基于现代计算机控制技术开发的旋转小翼[3-4]及惯性激励[5]，由于激励信号已知，可得到系统的传递函数，一般可采用正交多项式拟合、频域子空间、最小二乘复频域等算法进行模态阻尼辨识；对于固体小火箭激励和脉冲驾驶杆舵这类激励，一般采取多项式拟合算法进行数据处理[6]；对于大气紊流结构激励，一般使用增强频域分解算法和频域空间域分解算法。在实际颤振试飞中，根据飞机的具体系统和结构形式，考虑试飞安全、有效结果和经济的原则，选择合适的激励手段与数据处理方法。

1 小型民用飞机颤振试飞

小型民用飞机颤振飞行试验与其他类型飞机颤振飞行试验基本类似，由于飞机结构与系统较为简单，飞机基本不会使用电传系统，所以不存在气动伺服弹性的问题。由于飞行高度及飞行速度均较小，大部分为亚音速飞机，少部分喷气公务机可达到高亚音速，所以一般颤振试飞可不考虑马赫数的影响，高度选择上一般选取一个在大速度俯冲中可安全改出的合理最低高度，速度以校准空速为准进行。试飞方法采用逐步逼近的方法，每外扩一个速度点，计算该速度点下各主要模态的阻尼，通过所有已有速度点主要模态阻尼变化趋势来研判下一速度点安全性，直到将速度扩展到设计俯冲速度VD，其中每往前扩展一个速度，都需要飞机操稳试飞结合对飞机进行检查。

计算分析和风洞试验作为颤振试飞中速度扩展的前提以及重要支撑发挥着重要作用。由于小型民机结构较为简单，非线性特性不强，且飞行速度一般都在亚音速段，特别模型经过地面共振试验的数据修正后，基于结构有限元模型与非定常气动力模型的颤振计算准确度较高。风洞试验中，小型飞机速度较慢，有的飞机甚至直接使用全机模型在大尺寸风洞中完成风洞试验，消除了大部分模型缩比带来的误差，飞机颤振吹风试验结果具有极高的准确度。

小型民用飞机颤振试飞一般选择固体小火箭、脉冲驾驶杆和大气紊流的激励手段。运12F飞机在颤振适航审定试飞过程中采用了小火箭脉冲的传统激励方式[7]，是一种可靠性较高、理论基础完整、频带较宽且充分的激励，但这种激励有成本过高的缺陷。脉冲驾驶杆的激励方法只能对较低频带内的模态进行激励，且飞机速度较快时，获取的响应信噪比往往较差。随着工作模态分析方法的发展，基于大气紊流的激励方法在工程应用中取得了较好的应用[8]，这其中基于大气紊流激励的增强频域分解算法（enhanced frequency domain decomposition，EFDD）在ARJ21-700飞机颤振试飞中取得了较好的效果[9]。EFDD算法[10]已经在很多商业化软件中被应用，如B&K公司的Pulse软件模块中就包含该算法实现。频域空间域分解算法（frequency and spatial domain decomposition，FSDD）是王彤与张令弥于2006年提出的一种运行状态模态分析方法[11]，在部分飞机颤振试飞中也得到了应用验证。实际应用中发现，EFDD与FSDD算法对密频模态均有较好的辨识效果，但对于部分特别高频率的模态辨识中，会出现辨识结果不稳定的情况，阻尼辨识结果可能会有较大偏离。随着基于时域分解算法的发展，基于自然激励技术（natural excitation technique，NExT）[12]和经验模态（empirical mode decomposition，EMD）分解的模态辨识技术在桥梁和大坝结构辨识中取得较好的发展与应用[13-14]，基于EMD分解的辨识技术在小火箭激励响应中也取得较好应用[15]。将基于时域分解的算法应用到基于紊流激励的颤振试飞数据处理中是对基于频域分解算法的一种有力补充。

飞机的颤振适航性要求，是随着科学技术和飞机设计理论的不断发展而发展改进的。同时，适航规章条款也会考虑一定的社会成本经济性，从而才能在充分保障公众利益的基础上，促进民用航空事业的健康发展[16]。在保障安全的情况下，低速小型民用飞机颤振试飞中可采取一些经济性的方法来逐步完成包线扩展，验证飞机对CCAR23.629颤振条款的符合性。所以考虑经济性及安全性的平衡，以计算分析与风洞试验为支撑，以大气紊流激励为主、飞行员杆舵脉冲激励为辅进行结构激励，采用多种成熟的基于紊流激励的辨识算法进行颤振试飞是工程可接受的方法。海鸥300水陆两栖飞机和小鹰700飞机的颤振试飞中即采用该工程方法，在颤振试飞中，基于紊流激励的颤振试飞模态参数辨识的准确性和稳定性直接关系到速度扩展过程的安全性。以下就颤振试飞数据处理中常用的FSDD和EFDD算法及部分工程应用的基于NExT和EMD的模态辨识算法进行分析。

2 模态辨识算法

基于大气紊流激励的辨识算法中，基本都认为气弹系统的输入为类似白噪声的平稳随机激励，在实际工程中所关心的较短频段内大气紊流激励满足输入激励是平直谱的假设，自然界的脉冲激励基本也可认为具有平直谱。EFDD算法对响应谱矩阵进行奇异值分解，以奇异值所在峰值的奇异值向量为参考，计算峰值两侧各频率点奇异值向量的模态置信准则（Model Assurance Criteria，MAC）值，设定合理的MAC允许值，得到某阶模态的的增强功率谱密度函数，将增强功率谱密度函数经逆傅里叶变换后，在时域采用对数衰减法识别衰减系数与阻尼。FSDD算法也是对响应谱矩阵进行奇异值分解，通过最大奇异值所在的峰值附近的窄频带内构建某阶模态的增强功率谱密度函数，而后通过构造与增强功率谱密度函数对应的含辨识模态的响应谱矩阵表达式，通过最小二乘法辨识求解出该阶模态的频率和阻尼，所以FSDD是一种在有限条件下的简化方法，不需要进行逆傅里叶变换。基于NeXT和EMD的模态辨识算法考虑结构在白噪声载荷激励作用下的脉冲响应函数可由NExT获得，对获得的脉冲响应函数进行EMD分解，得到关心模态的单自由度脉冲响应函数，通过希尔伯特变换和最小二乘算法获得模态频率和阻尼。

这三种算法在计算上具有一些相通的特性。FSDD和EFDD算法均是通过频域分解算法得到单自由度的增强频域函数，而基于NExT和EMD分解算法通过时域分解获得单自由度模态时域衰减函数。FSDD方法也可以借鉴EFDD方法中采用MAC判定来求得增强功率谱密度曲线，这样比经验选择更加有效，同时FSDD方法中的振型计算也可以参考EFDD方法的奇异值向量加权平均法获得。EFDD算法得到单自由度衰减响应函数后也可以采用希尔伯特变换来进行模态频率与阻尼辨识，而NeXT和EMD算法得到单自由度衰减函数后也可以采用指数衰减法进行模态频率与阻尼辨识。也有学者得到单自由度衰减响应函数后采用时间序列法ARMA模型进行结构模态辨识[17]。

2.1 频域空间域分解算法

输出响应的功率谱矩阵可表示为：

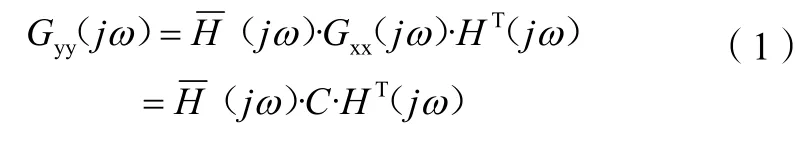
式（1）中：Gyy（jω）为响应谱矩阵，为Hermite矩阵；H（jω）为传递函数矩阵；C=Gxx（jω）为输入谱矩阵，由于输入的直平谱假设，C为实常数对角矩阵。

对响应谱矩阵取转置，有：

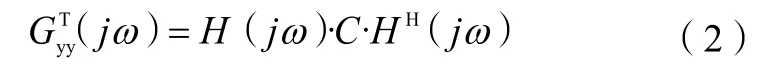
直接对为正规矩阵的响应谱矩阵进行奇异值分解，可以得到：

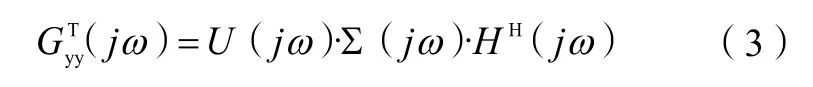
式（3）中：U（jω）为奇异值向量组成的酉矩阵；Σ（jω）为奇异值构成的实数对角矩阵。

将传递函数矩阵H（jω）表示为部分分式形式，在特定窄频带内，对响应信号贡献大的一般只有几个，响应谱密度矩阵可写成如下形式[10]：

式（4）中：sub（ω）为对这一模态贡献较大的频带；dr为一比例常数；ψr为模态振型；为该阶模态极点。

假设结构阻尼较小，这满足颤振试飞中模态的情况，即假设第r阶极点中结构阻尼ξr远小于固有频率ωr。在第r阶模态频率ωr的邻近谱线上，式（4）中后一项的分母远大于前面一项的分母，因此可以近似忽略，可得：

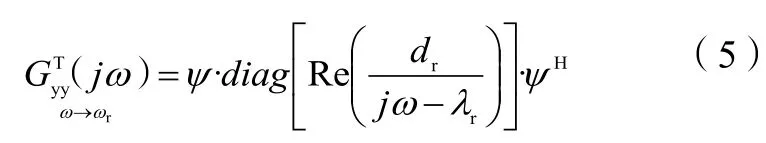
式（5）中：ψ为模态振型矩阵。

对比式（3）与式（5），多自由度系统模态振型在归一化以后为酉矩阵。所以式（3）中的奇异值向量与式（5）中的模态振型相对应，奇异值等于dr除以频率点到极点距离的实部。最大奇异值所在位置为，由于ξr为一小值，所以最大奇异值所在位置近似为该阶模态自然频率。实际应用中，所关心的窄频带内，第r阶模态的增强功率谱密度定义为：

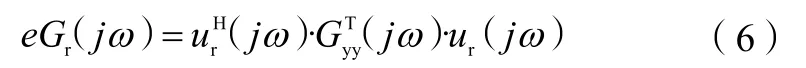
式（6）中：ur（jω）为第r阶左奇异值向量。

增强功率谱函数为一个单自由度函数，其正好是对应第r阶模态对应响应谱矩阵中的奇异值。

将极点表达式代入上式，变换得到：

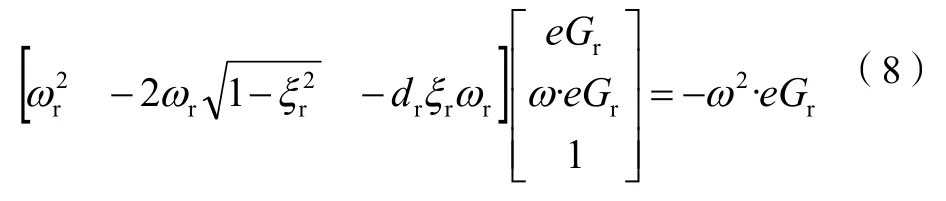
在关心的窄频带范围内，给定所有频率点频率和增强功率谱密度值，即可通过最小二乘求解得到该阶模态的频率和阻尼，从式（8）可知，拟合频率点应不小于3个，且通过式（7）可以给出拟合的增强功率谱数据，并可与原数据通过曲线绘图进行对比来判断辨识情况。模态振型与EFDD方法一样，可以由所选频带范围内各频点处奇异值向量通过奇异值加权平均获得。

2.2 增强频域分解算法

增强频域分解算法也是从输出谱矩阵的奇异值分解出发，方法与FSDD一样，如式（3）所示。在响应谱矩阵奇异值分解曲线中选定的峰值频率上，以该点处的奇异值向量作为模态参考振型向量，计算它与两侧各频率点处奇异值向量间的模态置信准则（Model Assurance Criteria，MAC）值，如下式所示：

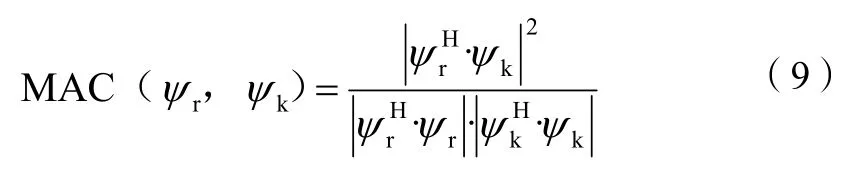
MAC表明了2个模态间的相关程度，一般在0～1之间，设定合理的MAC阈值，对于满足MAC值要求的频点，纳入增强功率谱曲线计算范围，该奇异值也就包含在了该阶模态频谱曲线中。最终，该阶模态振型通过所选频带范围内各频点处所选奇异值向量通过奇异值加权平均估计获得。最后在所选频带范围内采用式（5）得到该阶模态的的增强功率谱密度函数，将增强功率谱密度函数经逆傅里叶变换后，得到时域内的自由衰减函数（单自由度的相关函数），用来计算该阶模态频率阻尼。

式（10）中：δr为对数衰减率；r0为衰减函数的初始峰值；rp是第p个峰值。

则该阶模态的阻尼比为：

通过计算穿零点个数与时间的线性回归估计有阻尼自然频率fdr，则无阻尼自然频率为f0r：

2.3 基于EMD与NExT的辨识算法

NExT法的基本思想是：线性系统在白噪声激励下两点响应的互相关函数和脉冲响应函数的数学表达式完全一致。一般情况下，选取响应较小的测点为参考点，计算其他测点与该参考点的互相关函数，然后将计算出来的互相关函数作为输入数据，进行模态参数辨识。

将NExT法提取的脉冲响应函数进行EMD分解得到各阶ⅠMF分量，即为结构的各阶自由衰减响应，其表达式为[13]：

式（13）中：A0和φ0为幅值和相位初始值；ζr、ωr、ωdr为第r阶模态的阻尼比、无阻尼自然频率、有阻尼自然频率。

对该式进行Hilbert变换，得到该衰减响应的解析信号：

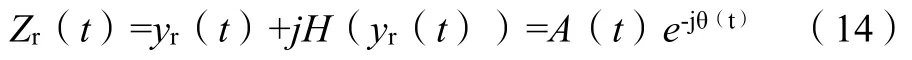
当系统的阻尼较小、频率相对较高时，上式中的幅值和相位可进一步表示为：

通过对上式幅值求对数和对相位求微分可得：

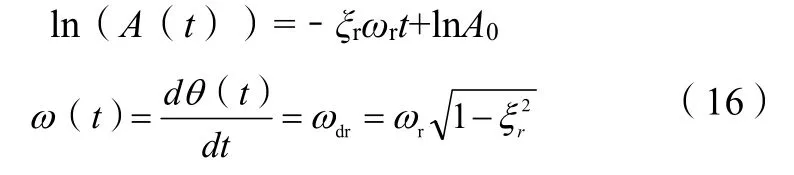
通过最小二乘拟合，可由上式得到该阶模态的固有频率ωr和阻尼比ξr，该方法无法求得模态的振型，需要实际应用中参考飞机的地面共振试验和颤振计算分析报告来判定具体模态振型形式。通过最小二乘拟合曲线的平直程度，可评价所提取的固有模态函数是否为单一主模态占优。

3 功率谱估计

从FSDD方法与EFDD方法的算法推导中可以看出，辨识算法的出发点均为响应的功率谱密度估计。基于EMD与NExT的模态辨识算法虽然是从响应的互相关函数开始进行，但互相关函数也可以通过互功率谱密度的反傅里叶变化获取。所以在各种基于大气紊流激励的模态参数辨识算法中，响应的功率谱估计都是模态辨识的基础。颤振试飞数据不同于地面试验或实验室试验数据，需要飞机在试飞状态点（一定的高度、速度及姿态）进行状态保持，特别是接近VD的长时间状态保持比较困难，所以一般有效试飞数据长度均有限，因此希望从有限样本数据中计算随机序列的真实功率谱，属于典型的估计问题。功率谱估计有多种方法，主要有非参数谱估计和参数化谱估计（现代谱估计），非参数的谱估计又分成间接法和直接法（周期图法），非参数方法为目前飞行试验中使用最为广泛的一种方法，这其中比较常用的方法为Welch方法。Welch方法通过分段重叠求得平均来降低估计方差，通过加窗平滑来减小偏度，集平均与平滑的优点于一身，但同时也带来了两者的缺点，是一种折中的方法[18]。

在实际颤振试飞数据功率谱估计中，数据长度和采样率一定的情况下，选择合适的FFT点数（数据块大小）是取得合理估计的关键。数据块取值小，则频率分辨率变小，对模态频率估计会有偏差，且密频模态不能很好识别；数据块取值过大，由于数据样本长度有限，平均次数不够，估计方差增大，则谱估计不够平滑，模态不容易选择，且阻尼估计值会有较大偏差。数据处理中可以选择奇异值分解曲线作为参考，通过不同块大小参数下的曲线对比，结合地面试验模态频率分布情况，选择合适的块大小。

某小型民机颤振试飞某状态紊流激励，不同块大小取值情况下，机翼部位振动响应功率谱估计矩阵的奇异值分解曲线对比如图1所示，数据长度为60 s，采样率为256，选择hanning窗函数，数据块重叠率为50%。依据该机地面共振试验结果，结合图1所示的功率谱奇异值分解曲线，该区域有4个可辨识模态。选用块大小为256个点，曲线光滑，但分辨率较小，且无法分辨出部分模态频率；选用块大小为2 048或4 096，则分辨率较高，但平均次数减少，曲线不够光滑，不易选取与拟合；选择1 024块比较合适，分辨率为0.25 Hz，曲线较为光滑，也包含所需模态。使用Welch法进行功率谱估计，窗函数、重叠率等参数的选择也可以参考块大小的选择方法。采用参数化功率谱估计方法，块大小确定后，阶数的设定也能以奇异值分解曲线为参考来进行确定，选择合适的阶数使得在需求和计算量方面取得平衡。通过多项颤振试飞实践发现，一般选取的合适数据段长度在32～64 s，在进行功率谱估计时，选取hanning窗或hamming窗，重叠率一般不小于0.5，分辨率选择0.25 Hz进行计算比较合适。

4 试飞应用

某小型民用飞机进行适航审定颤振试飞，采用大气紊流进行结构激励，全机安装25个加速度传感器，采样率256，选取高度2 000 m，各试飞速度点稳定状态数据32～64 s。分别使用FSDD、EFDD和基于EMD的辨识算法对紊流数据进行模态辨识，功率谱估计选用hanning窗，块大小1 024，重叠率0.75。

图2为垂尾一弯模态的频率-速度-阻尼（f-Vc-g）图，其振型如图3所示；图4为垂尾一扭模态的f-Vc-g图，其振型如图5所示。图6为平、垂尾某高频局部模态的f-Vc-g图，其振型如图7所示，取名为“平垂尾模态一”；图8为平、垂尾另一高频局部模态的f-Vc-g图，其振型如图9所示，取名为“平垂尾模态二”。

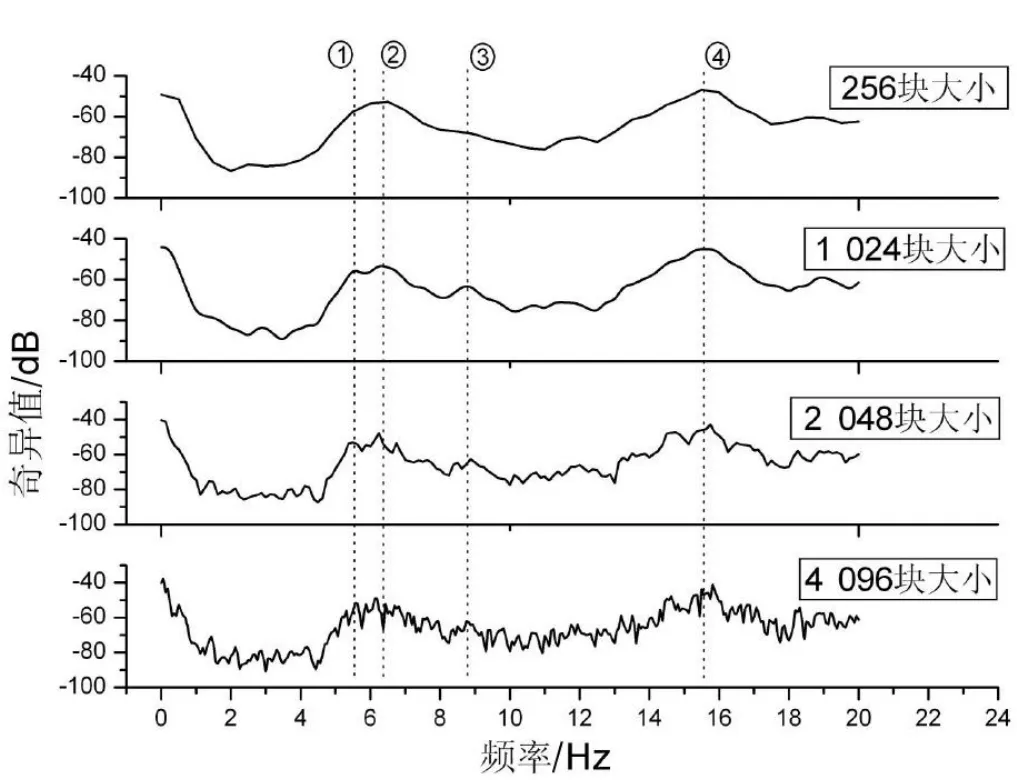
图1 不同块大小功率谱矩阵奇异值分解曲线对比

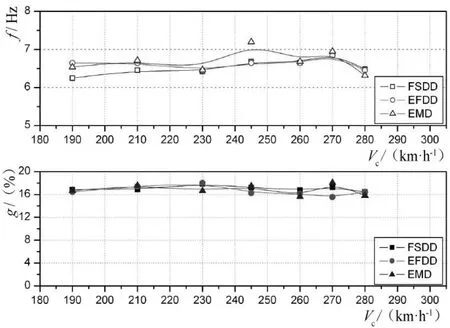
图2 垂尾一弯f-Vc-g图

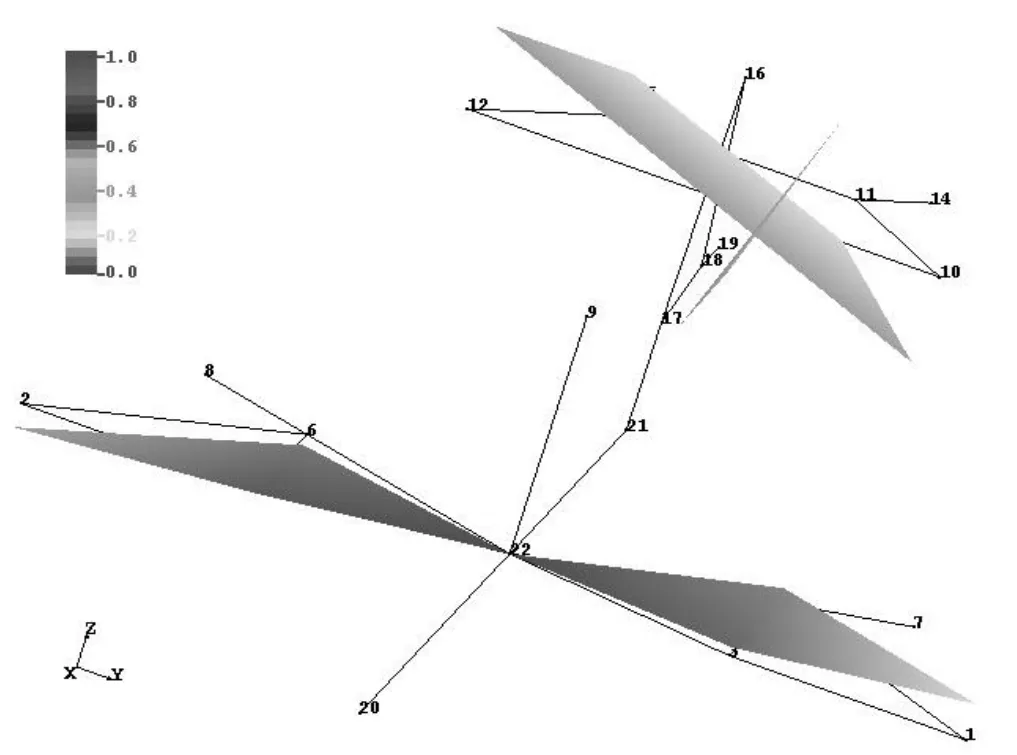
图3 垂尾一弯振型

图4 垂尾一扭f-Vc-g图

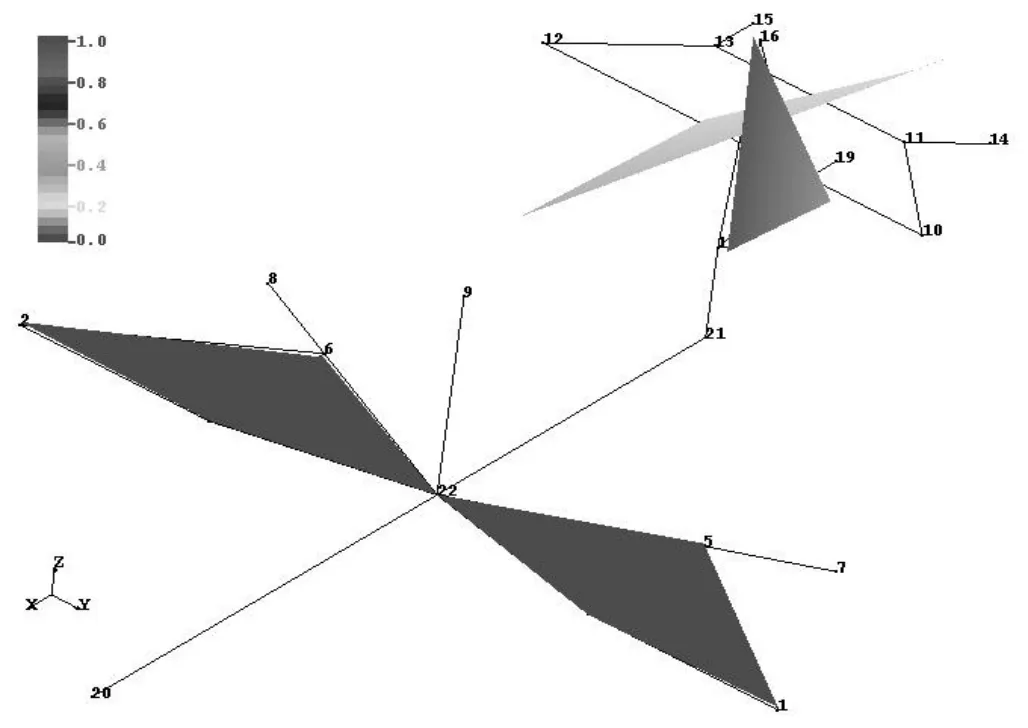
图5 垂尾一扭振型

图6 “平垂尾模态一”f-Vc-g图

图7 “平垂尾模态一”振型

图8 “平垂尾模态二”f-Vc-g图

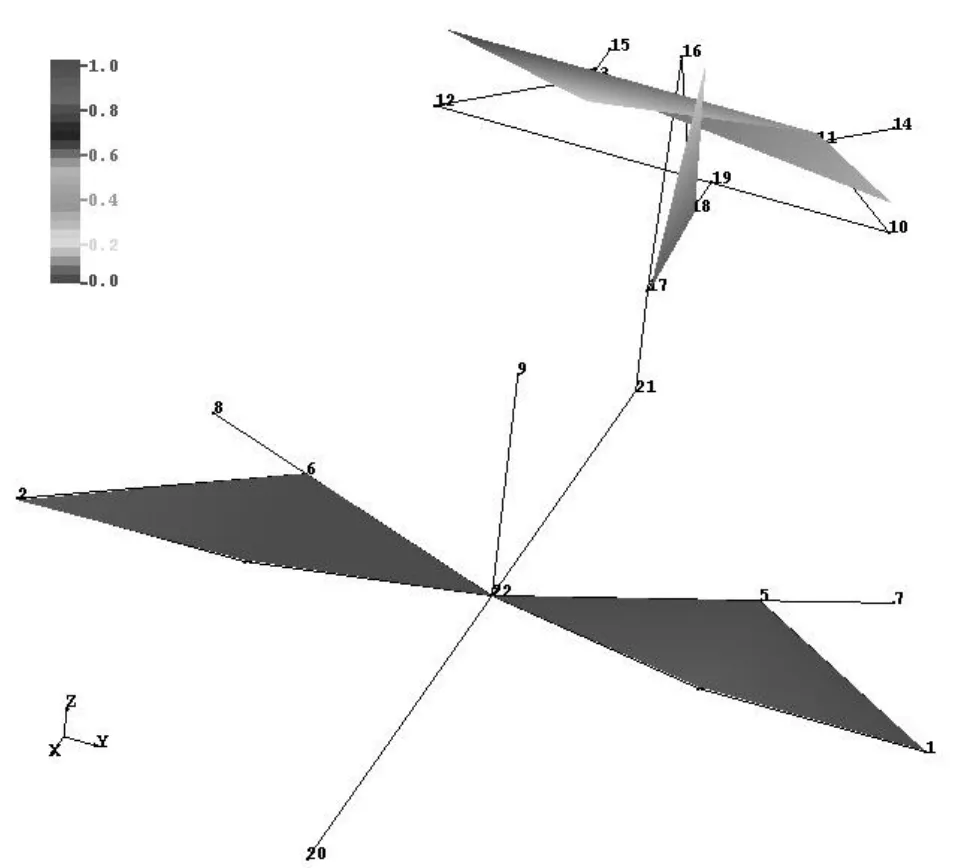
图9 “平垂尾模态二”振型

适航规章CCAR23.629（b）款规定中有规定，在速度VD时阻尼有合适的余量且接近VD时阻尼没有大而迅速的衰减。颤振试飞中一般参考国军标，阻尼余量参考值取3%。从图2和图4可知垂尾一弯和一扭这两个低频模态的频率和阻尼，采用三种方法辨识结果都比较一致，且阻尼均远大于3%，阻尼变化趋势平缓，没有陡然下降的趋势，满足规章要求。但对于平垂尾一模态和二模态这两个局部高频模态，从图6和图8可知三种方法的频率辨识基本较为一致且都比较稳定。高频模态阻尼辨识中，FSDD和EFDD这两种频域分解辨识算法的阻尼值受气流高频激励能量、数据噪声、人为经验等各种因素影响，造成阻尼变化较大且一致性较差，有部分辨识阻尼值基本到达3%，给速度扩展飞行决策及试飞安全评估带来极大影响；基于EMD的方法所得阻尼较为平稳，阻尼结果适中且可接受，但该方法严重依赖人员经验，辨识过程需要对数据进行各种滤波、筛选等前处理，EMD分解还面临端点效应和混频等因素困扰。所以在基于紊流激励的颤振试飞中，采用多种辨识算法进行对比分析是必要的，也有利于速度扩展安全和结果的准确性。

5 结论

本文所述三种基于紊流激励的工作模态辨识算法在小型民用飞机颤振试飞数据处理中可有效获取所需结构模态参数，适用于工程需要。对于环境激励模态分析，有必要用多种分析方法进行比较，有利于剔除虚假模态，避免模态丢失。同时多种方法分析结果对比可以稳定阻尼值，给颤振试飞速度扩展提供一个较宽阻尼范围参考，避免单方法阻尼估计偏离过大带来的风险。

试飞的特殊性，造成有效的试飞数据样本长度往往有限，功率谱密度估计对基于紊流的颤振试飞中模态参数辨识有重要影响，增加数据块长度往往造成平均次数减少，估计方差增大，缩短数据块长度又会造成频率分辨率下降，无法区分密频模态。实际颤振试飞数据处理中需要通过变参数分析并结合地面试验的结果来选取合适的功率谱估计参数。

工程实践中，EMD结合NExT进行模态参数辨识方法，是对EFDD与FSDD方法有利的补充，在部分功率谱峰值不好估计或质量较差情况下可选择该方法进行辨识，受限于EMD分解的质量，存在模态混叠与端点效应的影响，是一种可进一步研究发展的工程方法。