基于近端优化的永磁同步电机温度预测方法＊

岑岗 张晨光 岑跃峰 马伟锋 赵澄

（1.浙江科技学院，杭州 310023；2.浙江工业大学，杭州 310014）

主题词：永磁同步电机 温度预测 近端策略优化算法 强化学习

1 前言

永磁同步电机是电动汽车和混合动力汽车的核心部件之一，但其负载能力会受到温度等因素的影响[1-2]。为保证电机的安全、稳定运行，需要一种有效的温度预测方法帮助其提升在温度方面的抗风险能力。

在最近的研究中，Li 等人[3]通过构建基于半实物的温度等效模型实现了电机的温度预测，但该模型不能有效反映电机的真实运行环境。Kral 等人[4]构建了一种含有2个热节点的电机等效热传递模型，模型本身的温度估计失真却无法消除。Abdalla 等人[5]提出了一种永磁同步电机的集总参数热模型（Lumped Parameter Thermal Network，LPTN），该模型能够对电机的各部分温度进行计算。Wallscheid 等人[6]提出了一种永磁同步电机温度动态测量方法，但该方法要求电机在中、高速条件下运转。兰志勇等人[7]利用LPTN对永磁同步电机进行了温度场分析，但对于电机过热点的捕捉缺乏优化处理。Sciascera 等人[8]提出了一种LPTN 的变异热模型，相对于原始LPTN的计算量更小、预测精度更高，但是模型设计的复杂度依然很高。刘平等人[9]利用信号注入方法实现了电机的温度监测，但未给出电机过载情况下的温度估计结果。Wallscheid等人[10]利用磁链观测器实现了永磁同步电机的永磁体温度实时预测，使欧式范数最坏的情况小于10。杜爱民等人[11]利用有限元分析法建立了电机的电磁场有限元模型，得到了额定工况下电机各部件的温度分布。每个等效热模型都需要准确描述电机运转时的温度变化特性，这将导致经验丰富的设计人员需要在电机的热模型设计方面做出更多的努力。

人工智能技术在许多温度预测领域都得到了应用。Xu等人[12]提出了一种基于新型深度学习的公共建筑室内温度预测方法，验证了深度学习在室温预测上的有效性。Liu等人[13]提出了一种基于时间相关性的海洋温度预测方法，在预测性能上较支持向量回归（Support Vector Regression，SVR）和多层感知器回归（Multilayer Perceptron Regressor，MLPR）均具有更好的表现。Wallscheid 等人[14]将长短期记忆（Long Short Term Memory，LSTM）网络在电机温度预测领域进行了首次应用，但LSTM记忆块的引入以构建更加复杂的拓扑关系为代价。

针对上述预测模型或方法存在的问题，本文通过引入近端策略优化（Proximal Policy Optimization，PPO）算法[15]，并利用强化学习（Reinforcement learning，RL）网络完成模型构建，实现永磁同步电机的温度预测。

2 基于PPO-RL的温度预测模型

2.1 PPO算法原理

PPO最初应用于复杂智能体机器人的控制过程，其优势体现在智能体训练的监督过程中能够很容易地实现训练超参数的调节和梯度下降，在训练的每一步迭代中都会更新策略，尝试将训练目标的损失函数最小化，同时保证相邻2 次迭代产生的策略不会产生较大的偏差。PPO算法的目标函数L(θ)为：

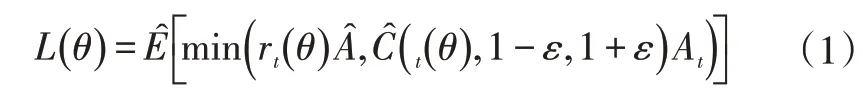
式中，ε为算法的超参数；rt(θ)=πθ(at|st)/πθold(at|st)为新策略与旧策略的比值；为策略更新后相对于旧策略的优势值，此处采用Crtic 网络的预测偏差表示；为平均值计算函数；C为截断函数，用来限制rt(θ)的更新范围；πθ(at|st)为更新后的策略；πθold(at|st)为旧策略；at、st分别为t时刻的动作和状态值。

目标函数L(θ)中，第1 部分是rt(θ)和的乘积，第2部分是将rt(θ)在区间[1-ε,1+ε]进行截断后与的乘积，最终得到未截断目标和截断目标中的最小值。此处，选取Actor 网络的损失误差作为PPO 的目标函数，通过最小化该目标函数实现电机温度的准确预测。

2.2 RL网络

为了实现电动汽车永磁同步电机主要部件温度的准确预测，考虑将强化学习通用的Actor-Critic 学习框架[16]作为本文预测网络的基础。Actor-Critic 兼备了Actor-Only 和Critic-Only 的优点，能够在训练过程的梯度更新中获得更好的估计量，改善局部优化问题，图1给出了该学习框架的一般结构。

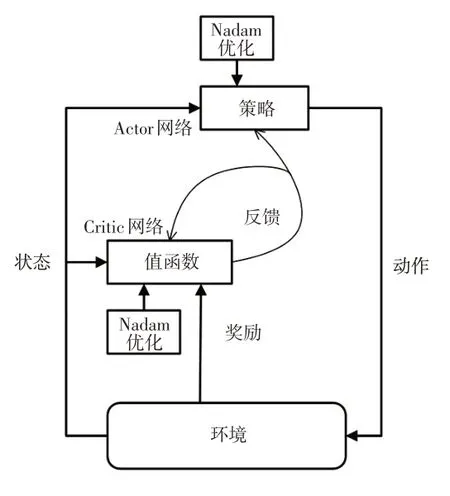
图1 Actor-Critic框架

Actor网络和Critic网络是该框架的主要组成部分，交互环境中的状态值来自永磁同步电机的记录数据集，动作值对状态值的动态选取是模型训练的基础。模型的预测结果由Actor网络给出，同时Critic网络给出预测结果优劣的判断，并将判断结果通过值函数反馈到Actor网络进行梯度更新策略调整，因此Critic网络在预测过程中对Actor网络的反馈显得尤为重要。网络的梯度优化由Nadam算法实现，而迭代过程的奖励值在每一次策略更新时均会进行叠加，可进一步反映训练的优劣。

2.3 PPO-RL预测模型

电动汽车永磁同步电机温度预测模型如图2 所示，Actor 网络和Critic 网络分别含有1 层输入层和1 层输出层，hi(i=1,2,…,5)为隐含层。图2 中，θ和θold分别为Critic 网络关于预测值和真实目标值的映射关系。

模型中各隐含层的定义方法为：

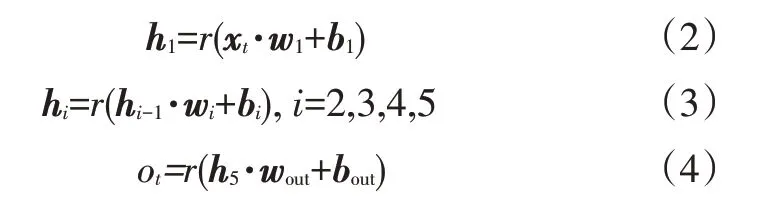
式中，xt为t时刻的输入数据矩阵；wi、bi、hi(i=1,2,…,5)分别为网络各隐含层的权重、偏置和隐含层；wout、bout分别为网络输出层的权重和偏置；ot为网络在t时刻的最终输出；r函数为relu激活函数。

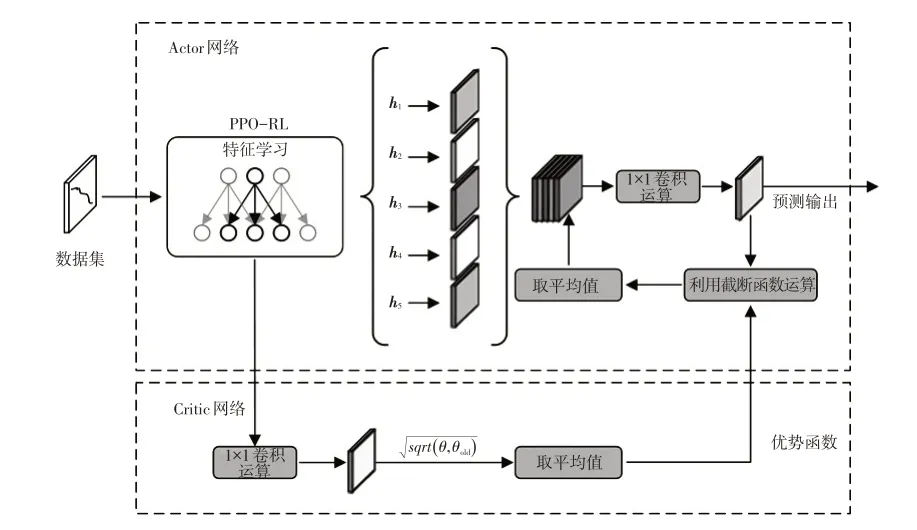
图2 基于PPO-RL的电机温度预测模型

设每次训练输入批次数量为N，预测过程如下：

a.根据式（1）确定训练模型的损失目标函数，该目标函数中的和rt(θ)分别为：

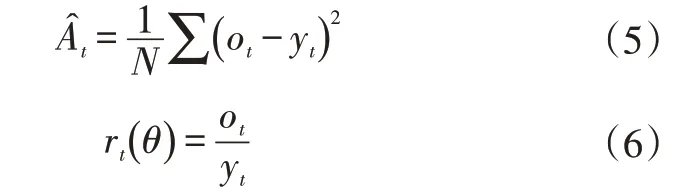
式中，yt为真实目标值。

b.根据图2 建立温度预测模型，其Actor 网络和Critic网络共享5层隐含层，且第1～5层网络神经元数量分别为512个、256个、128个、64个和32个，均使用relu函数作为激活函数。设输出层神经元数量为1个。

c.取步长为5，依次选取5×Nn（Nn为输入特征数量）的输入序列作为模型的输入数据，来预测下一时刻的目标值，通过选取步长为5，可以有效避免数据集中失真对预测精度的影响，降低预测误差，本文模型的输入特征数量为14 个。在逐次迭代训练过程中，根据每一步更新得到的和rt(θ)计算模型训练的目标L(θ)。

d.为了加速目标函数收敛，使梯度更快地达到全局极小值，利用Nadam 算法对训练的梯度进行优化更新。该算法相比于Adam 算法引入了t时刻梯度gt的校正量，并引入一阶矩估计mt的平均值替换其修正量用于计算更新后的梯度Δθt：

式中，ui为i时刻的一阶矩估计的动量因子；η为Nadam算法学习率；为t时刻梯度的二阶矩估计的校正量；ξ为接近于0但不为0的正数。

e.利用训练好的预测模型进行测试集的预测验证，最终获得模型的预测输出值。

3 评价指标

在预测试验中，选择合适的评价标准能够更直观地体现预测方法的性能表现。在许多经典的预测研究中，常采用均方根误差（Root Mean Square Error，RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）作为预测方法的定量评价指标[17]：

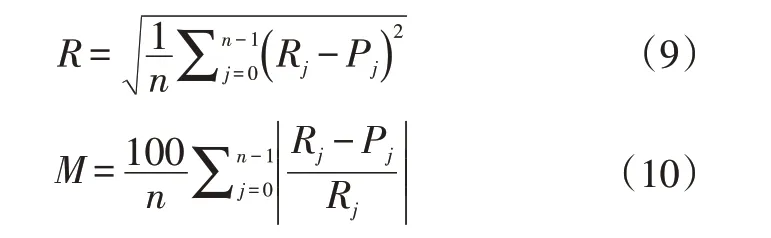
式中，R、M分别为均方根误差和平均绝对百分比误差；Rj为真实数据；Pj为预测的目标温度；n为测试数据量。

为了全面评估不同方法的预测表现，仅使用上述评价指标是远远不够的。范数具有长度的概念，在矢量空间中被描述为一个从原点出发的带有箭头的有向线段，可用于衡量向量的大小。本文通过引入欧几里得2 范数L2和最坏情况无穷范数L∞，可以讨论预测结果的逼近程度，进一步对不同方法的预测表现进行评估：

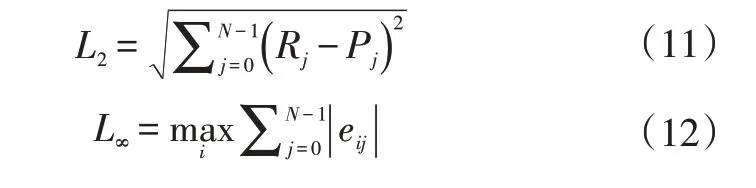
此外，采用拟合优度R2来计算预测结果的精度：

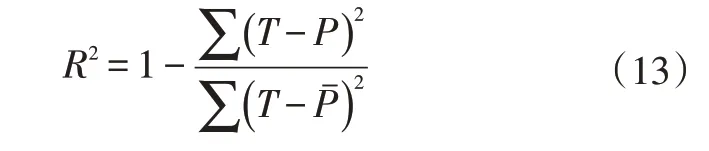
式中，T为真实数据；P为预测值。

4 试验分析

4.1 数据描述与处理

试验使用的基准数据来自Kaggle 数据科学竞赛平台，数据测量和收集工作由德国帕德博恩大学电力电子与电气传动系（LEA Department of Power Electronics and Electrical Drives）完成，且基准数据已规范化处理。基准数据标签包括环境温度Ka、冷却液温度Kc、电压d轴分量ud、电压q轴分量uq、电流d轴分量id、电流q轴分量iq、电机转速nmech、扭矩Tm、永磁体温度Kpm、定子轭温度Ksy、定子齿温度Kst、定子绕组温度Ksw和唯一ID 标识Sid。测试目标包括定子轭温度Ksy、定子齿温度Kst和定子绕组温度Ksw。基准数据共包含52 个测量会话，每个测量会话可通过Sid加以区分，所有测量记录均以2 Hz的采样频率在安装三相永磁同步电机的测试台上完成。

基准数据中的测量序列基本涵盖了永磁同步电机电热变化的完整过程。但为节约计算成本，同时覆盖电热变化全部范围，本文按照基准数据中每个测试会话的数据量平均分配30 000 条测试样本进行采样，并选取300条样本作为测试数据集，剩余样本作为训练数据集。

在上述数据集基础上，考虑部分额外特征量，包括以d-q坐标系为基准的电压分量的合成电压us、以d-q坐标系为基准的电流分量的合成电流is和电机功率Sel：

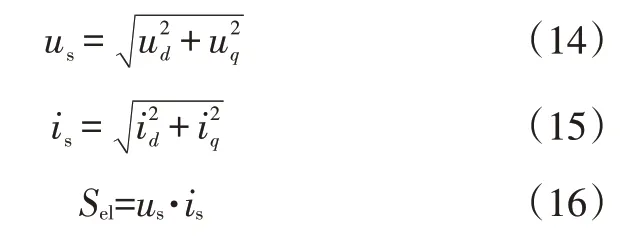
本文实际输入的特征需要除去Sid和拟合目标，因此实际的输入为1个含有14个特征量的张量。

4.2 试验环境及参数定义

使用64 位Windows 10 操作系统，计算机配置为3.4 GHz Intel Core i5 处理器，16 GB 内存。编译环境为Spyder 3.3.4，Tensorflow 1.13.1框架。

表1列出了试验过程中考虑的一些超参数，包括循环神经网络（Recurrent Neural Network，RNN）、LSTM、PPO-RL 和指数移动加权平均（Exponentially Weighted Moving Averages，EWMA）4种预测方法。

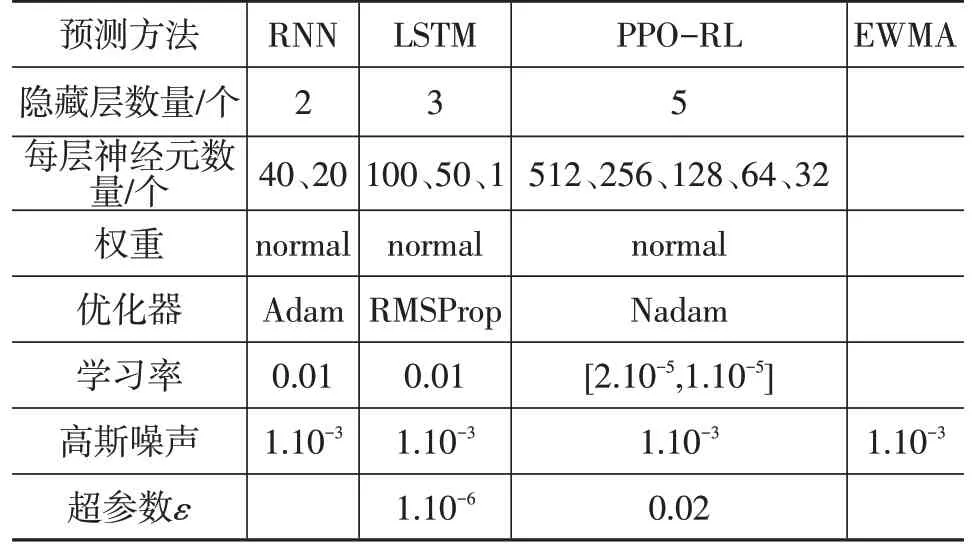
表1 超参数

除表1中能够自我解释的参数类型外，未具体提及的超参数应当被解释如下：预测网络在进行权重初始化时，最简单的方法是将权重的值随机分配到[-1,1]区间。当然，一些更为复杂有效的权重初始化方法也可以考虑，如单位正态分布或均匀分布。

4.3 试验结果与分析

利用测试样本进行测试，比较EWMA 网络、RNN、LSTM网络和本文预测方法对Ksy、Kst以及Ksw的拟合性能。

为了验证本文所提出的预测方法的可行性，分别采用上述4种方法进行30次训练迭代试验，得出各预测网络的预测精度、训练时间和预测时间如表2所示。从表2可以看出，PPO-RL网络的训练时长较长，其预测时间较LSTM 增加了0.27 min，这是由于其网络深度较深造成的，而且该网络的神经元节点数量最高达到了512个，这也表明PPO-RL网络具有较高的时间复杂度。

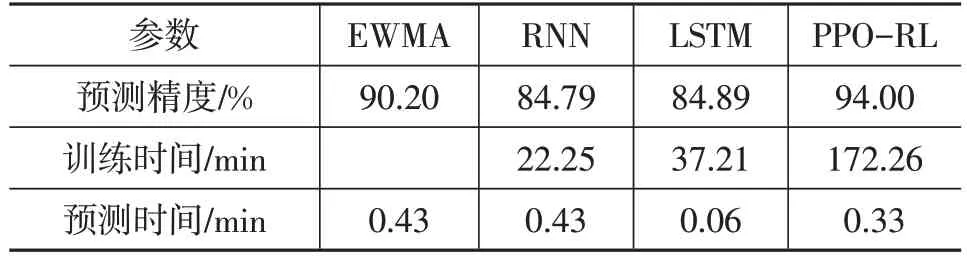
表2 定子轭温度预测精度和训练时间对比

定子轭温度迭代损失变化情况如图3 所示，由图3可以看出，在迭代周期为10次时，定子轭温度迭代的损失曲线趋于水平，说明模型能够实现稳定的拟合。

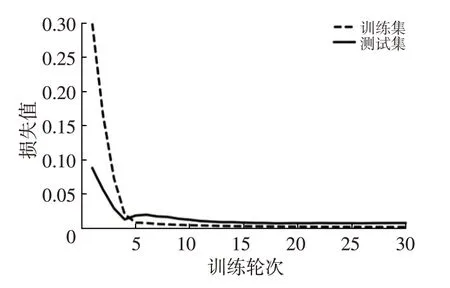
图3 定子轭温度迭代损失变化曲线

图4给出了4种预测方法对Ksy的拟合曲线。由图4可知，在几种预测方法中，LSTM网络拟合的曲线存在较大波动，与真实目标值偏差较大，而使用PPO-RL 模型得到的预测曲线能较好地符合目标曲线的走势。

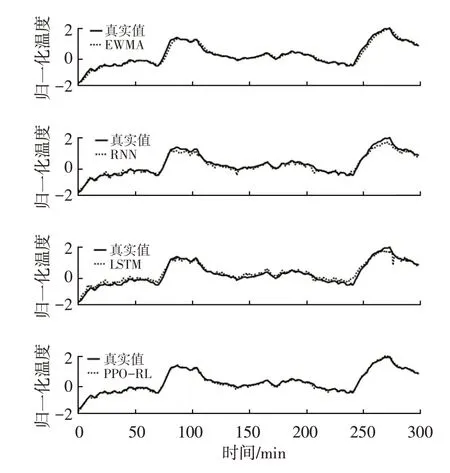
图4 定子轭温度拟合曲线对比

4 种预测方法对定子齿温度预测的精度和训练时间如表3 所示，迭代损失变化情况如图5 所示。由表3可知，虽然PPO-RL 训练花费了较长的时间，但是在迭代训练30次后，PPO-RL的预测精度仍能保持在90%以上，并且由图5可以看出，在迭代次数达到5次时，定子齿温度即可实现较好的拟合效果。

图6 给出了4 种预测方法关于定子齿温度Kst的拟合曲线。由图6可知，EWMA方法给出的预测目标曲线虽然在走势上与真实值曲线大致相同，但由于其自身伴随有较大的时延特性，因此难以为实时的永磁同步电机温度预测提供合适的观测点，PPO-RL模型在几种对比方法中依然具有较好的预测性能。

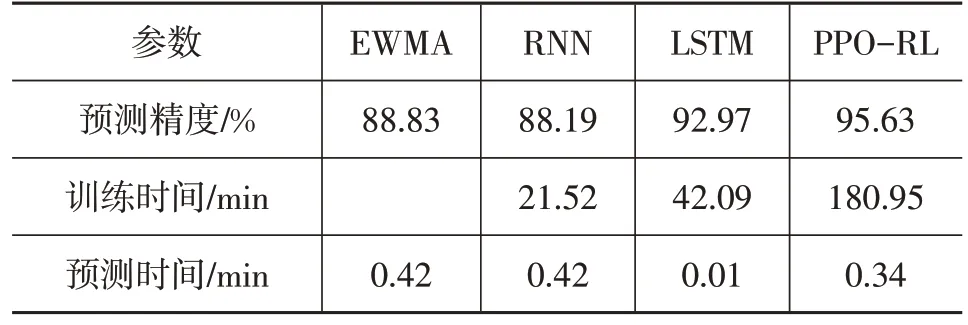
表3 定子齿温度预测精度和训练时间对比

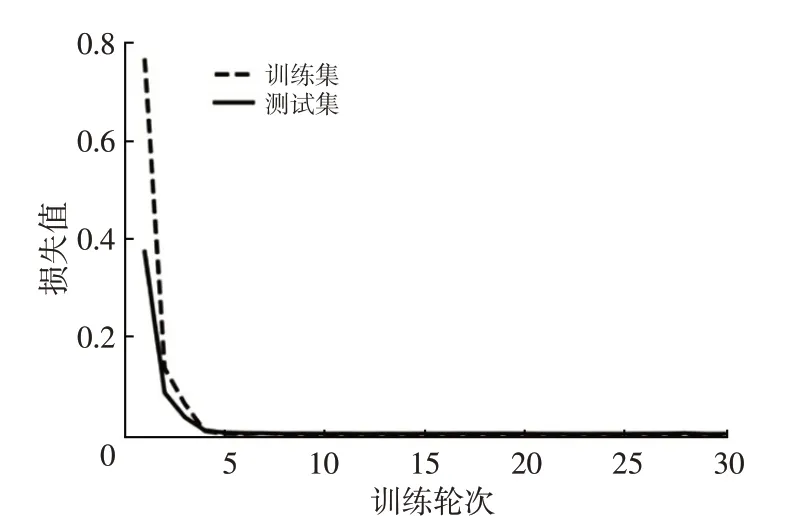
图5 定子齿温度迭代损失变化曲线

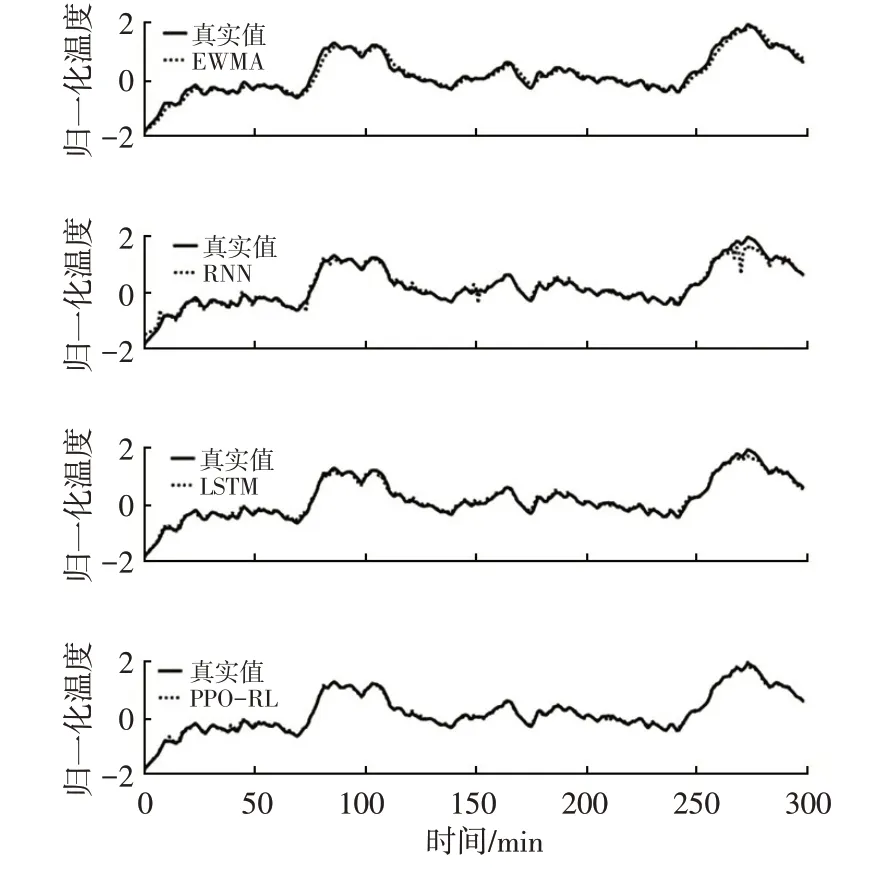
图6 定子齿拟合曲线对比

表4所示为4种预测网络对定子绕组温度的预测精度、训练时间以及预测时间对比结果。由表4 可知，PPO-RL 的预测时间达到了0.30 min，其预测精度为92.05%，并且该精度较LSTM和RNN的预测精度分别高出4.63百分点和8.43百分点。同时，其迭代的损失变化曲线如图7所示，由图7可以看出，PPO-RL在迭代30次后，能够得到较好的拟合性能。

图8 所示为4 种预测方法对定子绕组温度Ksw的预测曲线。由图6 和图8 可知，在预测目标Kst和Ksw的拟合曲线上，LSTM网络和RNN在预测开始时能够基本符合真实的目标曲线趋势，但结束时却存在较大的偏差。而在针对本文试验的3 个预测目标进行测试的过程中，PPO-RL拟合的目标温度曲线均表现出了较小的偏差。

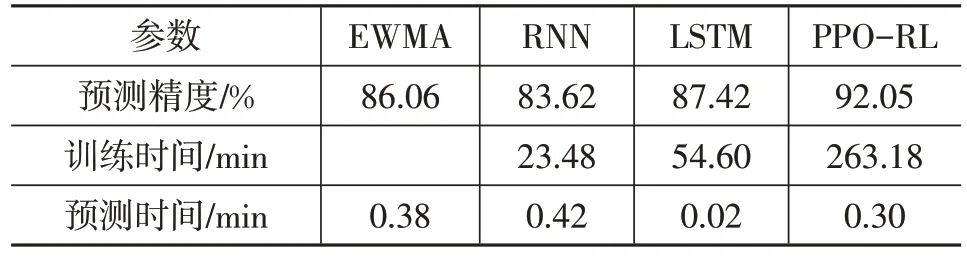
表4 定子绕组温度预测精度和训练时间对比

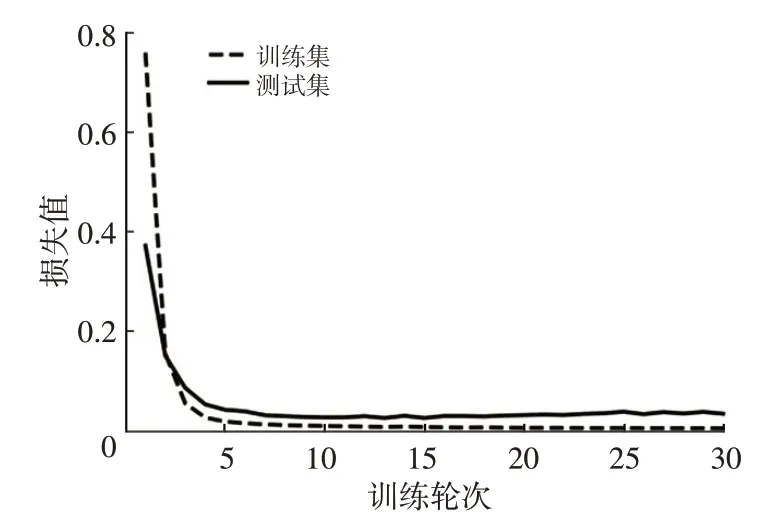
图7 定子绕组温度迭代损失变化曲线

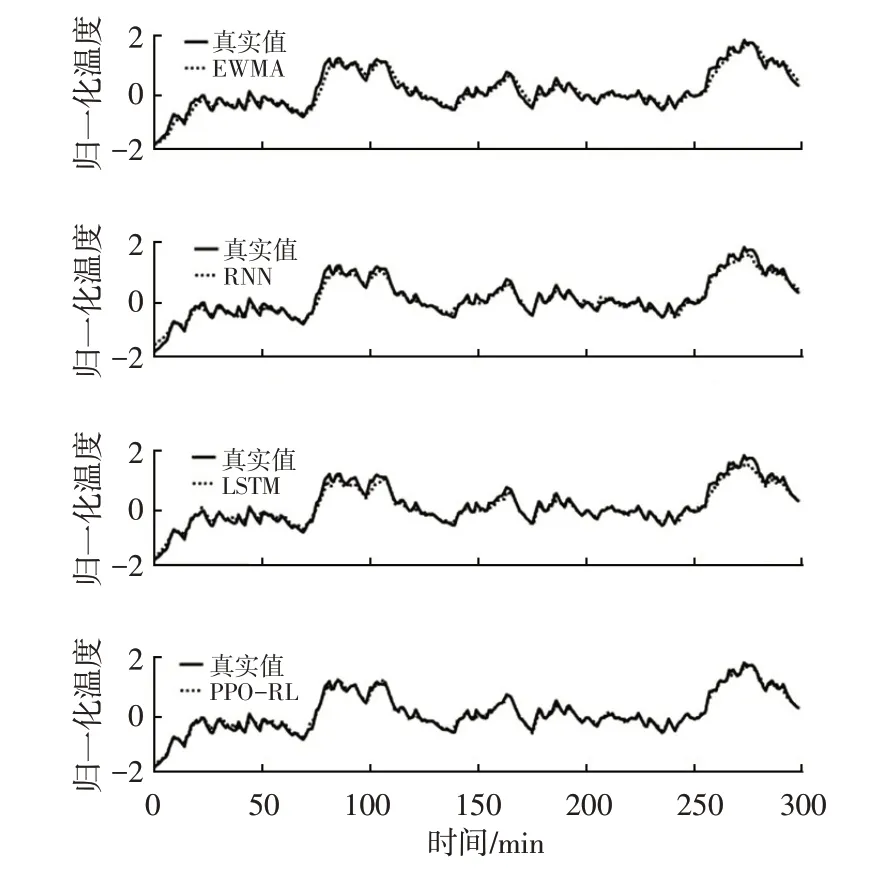
图8 定子绕组拟合曲线对比

为了进一步对比不同预测网络的温度预测性能，表5、表6和表7分别给出了针对Ksy、Ksw以及Kst的定量评价指标，其中包括R、M、2范数和无穷范数。

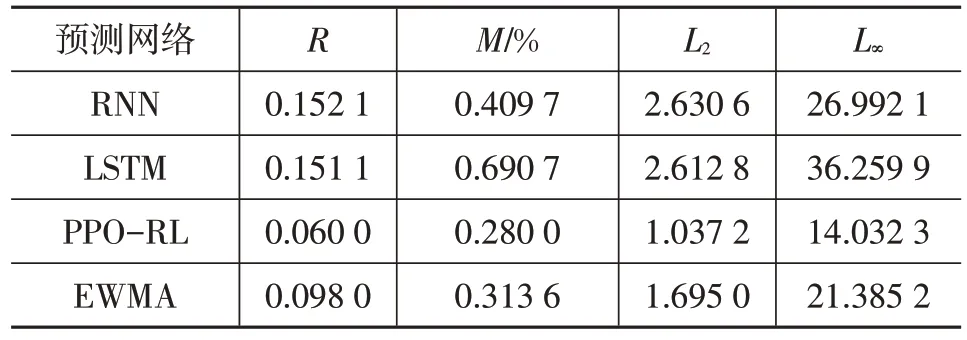
表5 定子轭温度预测误差对比

表5 结果表明，PPO-RL 在4 种定量分析指标中均处于最低值。在相同的条件下，LSTM在Ksy的温度预测方面没有表现出明显的优势，甚至在4种预测网络中的表现最差。进一步可以发现，EWMA 预测方法的预测性能似乎超过了经典的LSTM和RNN。

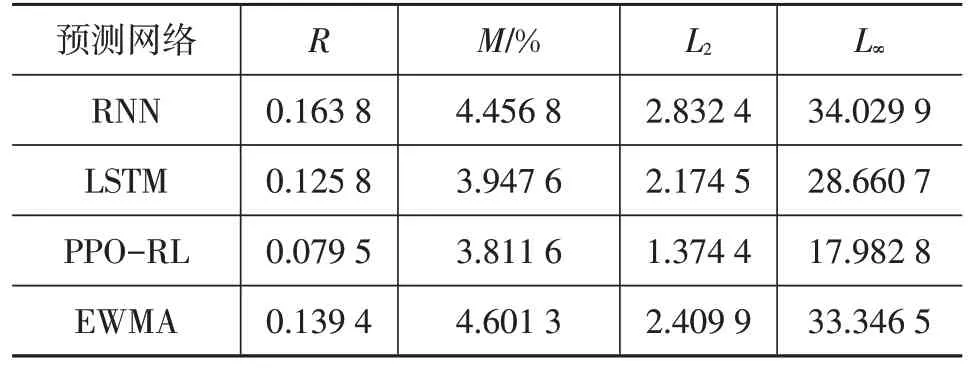
表6 定子绕组温度预测误差对比

表7 定子齿温度预测误差对比

由表6可知，PPO-RL相比其他3种方法整体上表现出良好的优势，PPO-RL 在4 种评估指标上均达到最低值，且其MAPE 与LSTM 和RNN 相比分别降低0.136 0%和0.645 2%，同时其无穷范数减少到接近LSTM的一半。

由表7 可知，PPO-RL 在Kst预测方面相比其他3 种网络具有更低的预测误差，其2 范数的值达到0.755 9，相比LSTM降低了0.459 2，在一定程度上表明其预测性能优于其他3 种经典预测方法。值得注意的是，LSTM网络虽然在预测Ksw和Kst时误差值较RNN 和EWMA 明显降低，但其在预测Ksy时却达到了最大预测误差。

5 结束语

本文借鉴了近端策略优化算法对目标函数裁剪的方法，构建了一种结合Actor-Critic 模型的永磁同步电机温度预测模型。模型利用Actor 网络实现数据集的训练学习，并采用Critic 网络的值函数反馈判断模型训练的优劣，通过30次迭代训练，使PPO的目标函数达到最小值，并对基准数据集进行采样和处理后，进行预测验证。将该预测方法与其他3 种经典预测方法进行对比分析，验证了提出方法的有效性。