基于数学核心素养下变式、变法练习设计方案探究
2021-03-24范萍莉


摘 要:变式教学的教育思想主要是通过数学解题理解数学知识、学会数学知识、学会数学方法的运用。有效的变式练习可以突出教学重点难点,突破数学教学难点。学生通过一题多变、一题多解能够掌握知识间的联系,容易激发学生自主学习研究的兴趣,从不同角度分析解答问题,解题过程由学生自己分析,增强学生的数学能力,优化认知结构,提高数学思维。
关键词:变式练习;一题多变;一题多解;自主学习
一、 引言
著名数学家波利亚曾说:“问题是数学的心脏。”数学教学就是问题的设计,课堂教学重点、难点的突出,突破是课堂一题多变的核心。有效的题目设计,题目变化更能让学生体会知识的实质,知识的联系。
变式练习的设计,就是有效地通过数学解题,教会学生去理解数学、深化认识、学会学习。有效的变式练习设计能够让学生对理论知识的理解、促进思维的提升。文章从教学实际,谈谈如何变式练习、一题多解,让学生理会到知识的内涵与联系,激发学生兴趣,从而有效突破教学重点、难点,提高学生自己学习的能力。
二、 变式练习的优点
(一)一题多变
通过变式练习中的一题多变,有助于帮助学生体会同一知识点在不同方法下的知识精髓,具体表现可从以下两点进行说明。
1. 一题多变对学生归纳能力和联想能力的培养
苏教版七年级有一些题目,要求学生看出题目的不同变式,要求老师在教学中对这类题目整理、比较,引导学生感悟题目的联系,从而培养学生思维的深度,即归纳能力,并逐渐形成数学思维方法。
小学阶段学生已经了解到高斯定理:1+2+3+…+n=n(n-1)2,学生在这个基础上可以归纳推理写出:
5+4+3+2+1=10,可以从一个数学模型归纳出一个算式,解决这个问题。学生从这个实际问题发现就是等差数列的运用,透过现象看到题目本质,从而培养学生的归纳能力,提升学生的数学能力。
例:有6个乒乓球选手参加单循环赛,两个选手比赛一场,共要几场?
变式1:在沪宁线上的一列高铁,从上海到无锡,中间有昆山、苏州两个站,请问从上海到无锡的火车票往返共有几种?
变式2:一次参加宴会,每两个同学互相握了一次手,本次聚会共有6为同学,共握几次手?
变式3:如果上题改成互送礼品,共要送多少份礼品?
2. 一题多变有助于学生逆向思维和数形结合思想的培养
利用上面的模型,把原本纯粹的代数问题,转化为几何问题,让学生学会从数到形,从形到数,数形结合思考,为今后的数形结合思想奠定基础。
变式4:一条线段上有6个点,这条线段上共有多少条线段?
变式5:一条直线上有6个点,这条直线上共有多少条线段?
变式6:如果从一个角的顶点,在内部引三条射线,图中共有几个角?
通过变式训练,学生学会了根据条件,归纳总结,学会数形的转化,使题目得到深层挖掘,让学生从数形转化过程中,体会知识的联系,以及今后数形结合的重要性,有助于培养学生的归纳创新能力,提高学生发现思维的積极性。
(二)一题多解
变法练习中一题多解有助于拓展学生的思维能力,从不同角度解析知识巩固知识,提升学生思维的深度、广度。
1. 一题多解有助于学生创造力和思维能力的提升
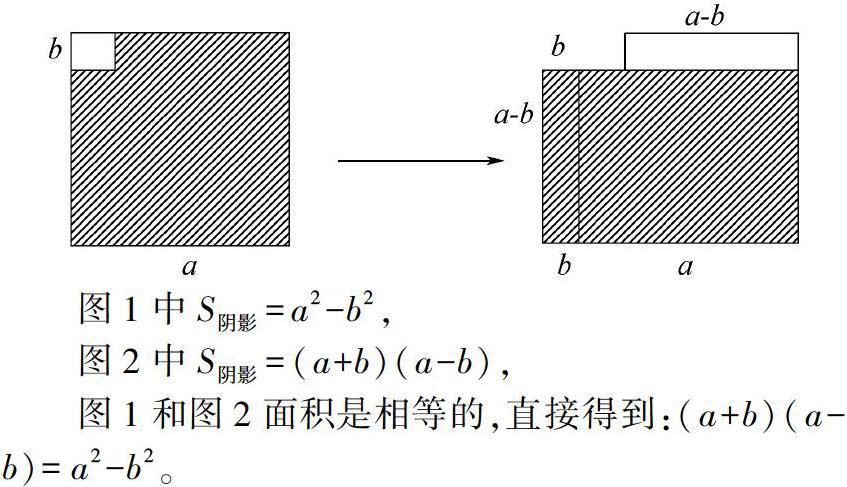
一题多解让学生的解题思路更清楚,多角度思考问题,提升他们的创造力和思维能力。如在证明平方差公式的时候,总结证明方法:学生通过具体数字的计算知道
学生在这个证明过程中能够感受到知识之间的联系,每一个新的知识,陌生的知识都可以通过已有的知识推导或者证明出来。同时通过代数式的计算感受到数的应用,图2学生体会到数有了形更为直观,反映出数形结合的具体性、直观性,传递给学生的信息是:以后无论做任何题目要多思考,用不同方式,多角度思考问题,解决问题的难易程度各不相同,因此要学会在学习过程中多思考,学会多种思考方式。一题多解以不同的论证方式,从不同角度反映条件、结论的联系,运用一题多解的方法长期思考问题,可以了解学生的思维过程、能力,还可以拓展学生思维,让学生了解知识之间的内在联系。
2. 一题多解有助于激发学生学习兴趣,提高自主学习的积极性。
素养是培养学生持续发展,自主思维能力,提高学生的良好的学科素养,培养学生的思维习惯和解题习惯。从不同角度、多层次、宽视角研究知识背景和问题特点,进行一题多解、一题多变。因此要学生养成深度思考的习惯,必须充分挖掘问题的隐含条件,培养学生思考问题的视角,提高探究意识和思维能力,从而达到融会贯通,走出刷题贪多的习惯,从量到精,全面提升学生的分析能力,成为真正的思考者。这样才会激发学生自主思考和学习,自主学习就是要学生能够参与,认识到题目思考的多途径,而不是教师一言堂。数学思想方法是最持久的,它能使人终身受益。掌握基本的数学思想和方法,能使数学更易于理解和记忆。培养学生的自主学习能力,让学生主动地学习,是一个漫长的过程,而且是渐进的过程,只有把知识方法的广度、深度帮助学生挖掘到位,才会激发自主思维提高思维能力。
三、 变式练习的教学方式
数学的核心素养在于激发学生的自我学习意识,提高创新能力。于是在教学过程中多角度思考问题是激发自主学习的关键。这样才会激励学生去思考。如:在讲授平方差和立方差的时候笔者以对比的方式让学生进行对比自主学习,通过学生任意数的平方都是非负数,于是得到被开方数的范围。在平方根所有的知识点回顾后,可以自主学习,做以下的变式:
在知识的归纳类比的基础上进行类比变式,学生进行自主探究,老师引导学生总结、归纳,从而提高课堂的容量,学生的参与度。提升课堂的效率,达到真正的学生为主的自我学习。
四、 变式练习中的题目设计
变式教学中一题多变、一题多解要注意题目设计,注重题目的方法引领,联系以及渗透思想。只有题目设计能够涵盖要讲的知识,有知识间的联系。这样既能复习知识,又能提高数学思维能力,学生举一反三,触类旁通。同时,学生在学习过程中能够做到在认知的基础上,提炼知识间的联系,概念本身,理解内涵,总结学习方法,从而激发学生学习兴趣,提升自学能力和水平。在上面的題目设计中包括了归纳法、变式练习、类比,学生类比模仿完成上面的知识,同时在解方程的时候用到了一元一次方程的基本知识,复习并巩固了一元一次方程的知识,老师归纳时要总结这些题目的思路方法:一、 归纳、总结,二、 类比、转化,高次方程要转化为一元一次方程,转化的思想。这样,学生今后在做题的时候就会注意到方法,自己学习归纳。良好的题目设计,会清楚地呈现知识方法的联系,数学知识结构的明确,会做到精讲精练,从而提高思维的深度,因此,题目设计中要注意思想方法渗透。只有数学的思维方法才能够让学生把握数学学习的核心,让学生学习效果最佳。
五、 结束语
数学的核心素养就是培养学生终身学习的能力,不断完善学生的认知。良好的数学教育教学就是促进提高学生的终身发展,培养学生的解题能力,完善思维能力。于是,教学过程中,通过变式、变法,即一题多变,一题多解,提高孩子对于知识的理解能力以及知识之间的内在联系,从而达到举一反三、触类旁通的效果。进一步通过一题多变、一题多解,提高学生对于知识的认知,拓宽学生的思维深度和广度,激发学生的自学能力。
参考文献:
[1]王在刚.一道月考题的多视角探究与自觉分析[J].中学数学教学参考,2019(4):35-36.
[2]刘娟.用题组设计感悟“增根”与“无解”[J].中学数学教学参考,2019(4):21-22.
[3]曾安利.变式教学中学生思维能力的培养[J].中学数学教学参考,2019(4):14-16.
[4]庄文芬.学生问题解决与创新能力的培养[J].中学数学教学参考,2019(4):12-13.
[5]林闯,朱能荣.对一道竞赛题的解法探究及思考[J].中学数学教学参考,2019(11):56-57.
作者简介:范萍莉,江苏省无锡市,无锡市凤翔实验学校。
