短除法教学争鸣

泮玲玲

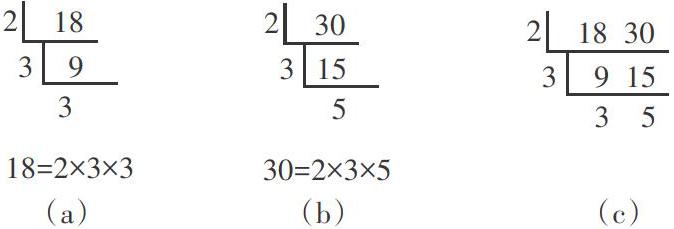
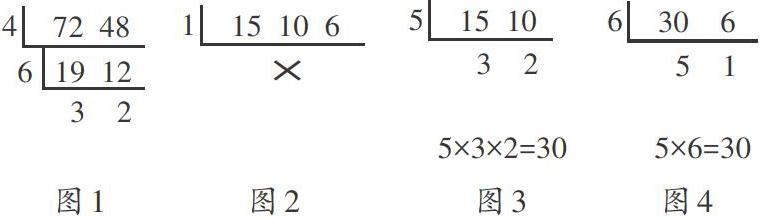
[摘 要]短除法作为计算两个数最大公因数和最小公倍数的一种偏方，不失为一个简明实用的方法，但是，其中涉及的算理颇为复杂，计算两个数的最大公因数和最小公倍数时，又有交叉的部分，不如列举法来得直观明了，因此在教学处理时需要慎重对待。

[关键词]短除法;算理;公因数;公倍数;最大;最小

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）08-0028-02

有幸拜读刘畅老师的论文《重在怎样教“短除法”》（下文统称为“《刘版》”）和陆晓林老师的论文《也谈“短除法”》（下文统称为“《陆版》”），读罢两文，笔者不禁掩卷而思。对于短除法，在现行课标部署下，教材一般作出两种处理方案：一种方案是将短除法这一知识点作为计算最大公因数和最小公倍数（后文简称“两最”）的拓展内容，作为番外篇单独编排在附录中，是否教学该内容让一线教师难以取舍。另一种方案是将短除法作为正式内容放入主篇幅，简省了算理分析只教算法，这样一来，虽然是必修内容，但是讲不讲解算理也让教师颇为踌躇。

《刘版》的看法是教短除法责无旁贷，并从算理的角度作了详细论述;而《陆版》则以实验班和普通班作为对象进行对照试验，倾向于放弃短除法的教学，认为“弃用短除法启用列举法才是两利相权取其重”。下面结合两位前辈的观点与笔者个人的教学实践浅谈个人思考。

一、短除法的算理剖析

运用短除法求算“两最”的理论基础是分解质因数，对两个数分别分解质因数，然后提取共有质因数（相同质因数要重复计算），这样一来就会罗列出两个数的全体共有质因数以及各自的独有质因数，最终将各个共有质因数相乘求出最大公因数（全体共有质因数相乘的积），全体共有质因数与各自独有质因数相乘求出最小公倍数。分解质因数的通用方法是短除法，如下图中（a）和（b）所示;在求“两最”的实际演算操作中，往往将分解质因数和筛选共有质因数合二为一，同步推进，将两个数放入一个短除号内进行同步分解，如下图中（c）所示，因此求几个数的“两最”的短除算式应运而生。

分解质因数的理论基础是算术公理，其内容是：任意一个大于1的自然数，都能分解成若干个质数的积，并且如果不计较排序，这样的分解式是独一无二的。显然，将一个数分解质因数后，得到的质因数乘式是唯一的，即任何一个数的质因数的大小与数量是固定的，因此，两个数的共有质因数的大小以及数量也是固定的，剩下的独有因数也是不变的;另一方面，由于每个数都是通过一步步做除法求出质因数，各个质因数之间是相乘的关系，这也证实了利用“乘积”求出“两最”的合理性。求“两最”的短除法与分解单个数的质因数如出一辙，唯一加以改造的是，利用“两个数的所有共有质因数是它们最大公因数的因数，两个数的最小公倍数是它们所有共有质因数和独有因数的乘积”这一定律。

现以计算18和30的“两最”为例来阐述。把18和30分别分解质因数：

（1）求它们的最大公因数的原理剖析：

18=2×3×3

30=2×3×5

由分解质因数的结果可以直接判断，18和30的共有质因数为一个2和一个3，于是全体共有质因数的乘积为2×3=6。毫无疑问，这个乘积是18和30的公因数，且这个乘积是将所有共有质因数求积得出的，它必然是公因数中最大的那个。如此，两数的最大公因数必然是两数所有共有质因数的乘积。

（2）计算两数最小公倍数的原理剖析：18和30的所有公倍数，一定都是18的倍数，根据倍数的传递性，势必同时是18的所有因数（包括非质因数）的倍数，同理，18和30的所有公倍数也一定是30的倍数，同时也是30的所有因数（包括非质因数）的倍数，等于是两个数所有因数的乘积的倍数。而我们要求的是最小公倍数，所以，其中包含的质因数应该尽可能少，唯一的可能是在所有的共有质因数上做文章，对每个共有质因数只算一次，不重复计算，于是18和30的最小公倍数=2×3×3×5=90。这个乘式中，2和第一个3是两数的共有质因数，第二个3和5分别是两数的独有质因数，为了确保结果是两个数的公倍数，要一一计算。不言而喻，两个数的最小公倍数，其实就是两数所有共有质因数与独有质因数的总乘积。

二、“短除法”的教学反思

1.短除法是小学生的必备技能。短除法的格式简洁直观，充分體现了求“两最”的流程、算理、技巧，算式美观整齐，易学易懂易操作。实践证明，学生在求“两最”时，乐于使用短除法。比如：在“求最大公因数”的综合应用题中，计算、约分等步骤，一般都是处理两个数，按照短除法的原理，先预判两数是否为2、3、5的倍数，然后直接用两个数的共有质因数进行整除，一步步化为最简分数。再如解答“最小公倍数”应用题时，在计算、分母通分时，用短除法更容易找出两个分数的最小公分母，步骤简练，计算的效率和准确性也有了保障。

2.不教算理，只学算法。从教材承担的功能来说，无论是正式篇章还是插叙的内容，通常都安排在列举法之后，以“小窍门”的形式出现，这样的编排设计，目的显而易见，重在“算法”而非“算理”，通过对短除法的学习和掌握，使学生用惯这种求“两最”的方法，牢牢记住短除法的格式和流程，以及短除收尾的特征和“两最”的具体计算方法。笔者通过实践发现，用短除法求“两最”，只要不深挖算理，只是单纯学习算法，学生学起来速度惊人。运用短除法的要领是确定每一步整除的除数，根据教材的不同意图，可采用三种方案来处理：第一种是用两个数的共有质因数去一步步整除;第二种是用两个数的公因数去整除;第三种是先观察两数，直接用2、3或5等质数去整除。三种方案大同小异，确定除数时通常是从质数2、3、5开始，这样能迅速确定质因数。笔者在教学实践中发现，第三种方案更加容易上手。

3.短除法有一定的灵活性。如在求取最大公因数时，每一步提取的公因数不一定非要是质数，也可以是合数，只要这个合数是待测数的公因数即可，大小不限，如果能够一步到位找准两数的最大公因数也未尝不可，如果不能就一步步检索完两个数的所有公因数，尽可能用最少的步骤快速找完所有并列的公因数。值得注意的是，与列举法不同，用短除法每一步找出的公因数（合数）都是互斥的，互不交叉包含。如图1，对72和48短除时，第一次短除提取的公因数是4，第二次短除提取的公因数是6，两数独立互斥，各自包含一个质因数2，72和48的最大公因数就是这两数的积：4×6=24。由此可见，短除法每次提取的公因数可以是合数，大小不限，但是一直要除到剩余因数互质为止，如上例中剩余因数为3和2，互为质数，说明短除已经触底。

另外，在求多个（三个及以上）数的最大公因数时，方法相似，可以将三个数一并短除;但是，在求多个数的最小公倍数时，则不能一并短除，而要两两短除，先求出两个数的最小公倍数，再用这个最小公倍数与第三个数短除，求出三个数的最小公倍数。如图2、图3、图4。

三、两种观点的冲突与协调

《刘版》认为“没有学习分解质因数也可以直接学习短除法”，增设了一个短除法的“过渡形式”，显而易见，所谓的过渡形式就是分解因数。笔者认为这样做有悖常理。理由如下：

其一，所谓的“过渡形式”，无非就是将一个数改写成多个数的积，只不过偷梁换柱用“因数”代替“质因数”，达到去质因数化的目的。然而，按照算术原理，一个数只有分解成多个质因数的积，且忽略顺序时，表达式才是唯一确定的。而若按照“过渡形式”写成因数的乘积，那么表达式则变化多端。如文中所列举的两数24和30，如果只是分解因数亦可写成24=1×4×6，30=2×3×5，如此一来，就会得出两数没有公因数的谬论。显然，用“过渡形式”取代分解质因数是欠妥的。

其二，文中提出，采用“过渡形式”寻找的公因数是“互斥”的说法，也站不住脚。其实，利用分解质因数法求出的共有质因数确实互斥，但却可以重复（如左短除式中重复出现的3个2）;而在做短除法的过程中，可以用非质因数去整除，这样就会出现相互包含交叉的情况（如右短除式中的除数4和2）。

其三，文中认为教短除法，只需要教会学生记住“列举法的公因数和互质这两点”，也经不住推敲。“列举法找出的公因数”是两个数的所有公因数（可以是合数）;与利用分解质因数法找出的两个数的共有质因数（必定是质数）是两码事。如72和54，列举法找出的所有公因数是1、2、3、6、9和18，而分解质因数后找出的公因数只有2、3和3，一律为质数。在计算“两最”时，两数的最大公因数只能是所有共有质因数（相同数字重复计算）的乘积2×3×3=18，而非列举法下所有公因数的乘积。

《陆版》中“弃用短除法启用列举法是丢卒保车”的观点，是将两种办法视为互相矛盾，好像教了短除法就会削弱列举法的影响，其实列举法只是一种基于公因数定义的基本方法，完全是按照“兩最”概念来演绎的，通过“罗列”出所有共有因（倍）数，从而找出最小和最大，强化列举法，重在对概念的回顾和理解，而不是机械重复查找的程序。

至于通过列举法可能让学生记住某些数的特性，做题时连估带猜一下子想起“两最”，这与方法训练无关。其实短除法之所以只是出现在附录中，就是考虑到算理理解上的困难，并不是否定短除法的价值。

（责编 吴美玲）