半开式离心叶轮气动阻尼的影响规律研究*
2021-03-24陈旭东杨树华王晓放刘海涛
陈旭东 杨树华 王晓放 刘海涛
(1.大连理工大学能源与动力学院;2.沈阳鼓风机集团股份有限公司)
0 引言
高压比、大流量、高效率、宽运行工况是离心压缩机设计的发展趋势[1]。复杂的运行工况带来的各种激振力可导致叶片动应力过大,从而引起叶片的高周疲劳破坏,疲劳破坏已是压缩机主要的破坏形式之一[2]。准确计算叶片的动应力是叶轮强度设计中的重要问题[3]。由于离心压缩机叶轮结构的振动模态密集,叶轮转速变化等因素影响,使得气流激振力的频率范围宽泛,叶轮共振校核难以完全满足要求。对于不满足共振要求的振动模态,需要进一步进行详细的叶轮动应力计算。叶轮结构阻尼的计算是否准确直接决定了叶轮动应力的计算精度。
对于半开式离心压缩机,叶轮总阻尼包括材料阻尼和气动阻尼。国外学者在叶轮阻尼的实验测量方面做了相关研究,Kammerer[4]通过实验测试得到了某离心压缩机叶轮的阻尼,以及材料阻尼和气动阻尼在总阻尼中所占的比例。Zemp[5]等利用类似的实验方法,研究了某离心压缩机的气动阻尼以及材料阻尼。相关实验测试的主要方法是:首先在真空环境中测量叶轮的阻尼,此时得到的是材料阻尼。假设材料阻尼是常数,再测量实际运行工况下的阻尼,从中减去材料阻尼部分即可得到气动阻尼。这种方法得到的总阻尼虽然比较精确,但实验测量很难考虑叶轮的所有模态以及机组的各种工况,并且实验成本也比较高。此外,假设材料阻尼比在各种工况下是常数也并不合适,Rao[6]得到了材料阻尼比与结构应力幅值的非线性关系。因此,采用实验测量得到的材料阻尼和气动阻尼的比例可能与实际情况差别较大。
利用数值计算方法准确估计不同工况下叶轮的气动阻尼成为关键问题。Parthasarathy[7]利用数值计算,得到了某超音速风机叶片的气动阻尼,并研究了叶间相角对气动阻尼的影响。池志强[8]通过数值方法分析了风力机柔性叶片在多种隐态风速下一阶模态的气动阻尼。相关研究[9-10]主要针对轴流透平,对离心透平的研究较少。由于转子叶盘的结构特点,轴流透平的叶片往往呈现行波型振动,特别对于轴流叶片一类高而短的结构,可假设所有叶片均固支于其根部振动,各叶片以同样的频率和振幅做简谐振动,相邻叶片的振动只相差一个叶间相角,该方法被广泛应用于轴流叶片气动阻尼的计算中。但对于离心叶轮结构,因其叶片展向短而弦向长,叶-盘振动必须整体分析,不同节径的振动不仅叶间相角不同,频率亦发生变化,故离心叶轮气动阻尼的分析方法与轴流叶片有所不同[11]。近年来,工业离心压缩机叶轮的疲劳破坏时有发生,叶轮结构的疲劳强度校核是技术关键[12],对离心叶轮气动阻尼特性的深入研究有助于提高叶轮动应力计算的精度,进而提升叶轮可靠性分析的技术水平。
本文首先介绍了气动阻尼的数值计算方法。通过模态分析,得到叶轮的固有频率、振型等数据。然后通过线性插值的方式将振型数据传递到流体仿真模型中,进行气动阻尼计算及分析。在此基础上,研究了叶片振幅、压缩机进口的流量、介质温度等对叶轮气动阻尼的影响。
1 气动阻尼计算方法
叶片表面的非定常气动载荷阻碍叶片振动时,气动载荷做负功,消耗结构振动能量,即气体介质具有正阻尼效应;相反,气动载荷对振动中的叶片做正功时,将使叶片振动能量增加,引发叶片的颤振。由于小幅振动引起的流场扰动具有线性特点,所以在叶片一个振动周期内,叶片表面对流体所做的功(即阻尼耗功)为

式中,t0是一个振动周期的开始时刻;T是振动周期;p是叶片表面压力;v是振动速度;n是叶片表面的单位法向量;A是叶片表面面积。叶片振动的周期、频率、振型等振动数据,由叶片的模态分析得到。根据等效黏性阻尼的定义[13],叶片气动阻尼比为

式中,U0为叶片一个振动周期内的最大变形能,定义为
式中,v是叶片体积。
本文采用流固弱耦合方法来求解气动阻尼。流固弱耦合方法的主要思想是分别求解结构方程及流体方程,利用线性插值方法将叶片的运动施加到流固耦合边界上,实现叶片在流场中的振动。由于Moffatt 和He[14]假设叶片的模态和固有频率不受气动载荷的影响,因此在结构动力学分析中只需考虑无阻尼自由振动。主要过程分为以下3步:
1)计算叶片的固有模态,得到振型及频率;
2)利用线性插值方法,设置最大振幅,将叶片按某阶固有振型振动的运动规律施加到耦合边界上,对流场进行扰动;

3)计算流场,得到非定常气动力,并结合已知的叶片振动位移,得到一个叶片振动周期内的非定常气动功。
气动阻尼计算利用的是傅里叶变换法(Fourier Transformation Method)。傅里叶变换法的主要思想是,在不同时刻的情况下,相邻节距边界是具有周期性的。这种方法不需要储存整个周期所有节距边界上的信号,只需储存傅里叶系数Am来得到任意时刻的解[15]。时间傅里叶级数展开如下

这种算法需要利用至少两个叶片通道,如图1 所示。计算中,采集的是相邻两个叶片通道交界面上(边界2)的傅里叶系数。交界面离周期边界远,信号质量高,计算比较准确。

图1 叶片通道简化模型Fig.1 The simplified model for passages

图2 相邻振动叶片间的相位差Fig.2 The phase difference between adjacent vibrating blades
对于典型的叶轮机械气体动力学问题(即叶片颤振和强迫响应),叶片-轮盘结构通常为周向匀速旋转的循环对称模式。对于这类叶片振动分析,相邻振动叶片间的相位差如图2所示,它可以表示为


2 叶轮模态分析
本文研究对象为一离心压缩机半开式径向叶轮,其出口直径1 179mm,出口宽度90.39mm,叶片数为19。由于叶轮是循环对称结构,可以采用叶轮扇区模型进行有限元分析。图3是叶轮有限元分析模型,叶轮叶片部分采用结构化网格,轮盘部分采用非结构化网格。考虑叶轮离心力的影响,采用有限元分析软件Ansys进行模态分析。叶轮一阶模态频率为384.6Hz,一阶模态振型如图4所示。

图3 叶轮有限元模型Fig.3 FE model for impeller

图4 叶轮一阶模态振型Fig.4 Deformation for the 1st impeller mode
3 半开式离心叶轮气动阻尼分析
3.1 气动阻尼计算参数和设置
叶轮流体域和固体域交界面网格节点不一一对应,需要通过线性插值的方式,将叶片振型的节点位移数据传递到交界面上的流体域网格节点。额定工况下,叶轮的进口总压为99 000Pa,进口总温为298K,质量流量为54.88kg/s,转速5 556r/min。Ansys CFX中叶片通道的网格划分如图5所示,单个通道网格单元总数约为14万。计算工质为理想空气。由于离心叶轮中存在较强的逆压梯度,其可能导致流动分离。而SST模型对于强逆压梯度的边界层流动和流动分离预测有很好的表现,故湍流模型采用SST模型[15]。CFD计算模型如图6所示。

图5 叶片流道网格Fig.5 Mesh of passage for CFD calculation

图6 CFD计算模型Fig.6 CFD calculation model
瞬态CFD计算以定常计算结果为初值,计算中,一个振动周期设置70 个时间步。额定工况下,叶轮一阶模态的气动阻尼计算结果如图7 所示,由式(1)计算得到气动阻尼在一个振动周期内的耗能为0.000 284J。根据式(3)可得叶片的应变能为U0=0.018 2J,再由式(2)得气动阻尼比为0.001 24。

图7 气动阻尼耗功收敛曲线Fig.7 Convergence for aerodynamic damping work
为了尽量消除网格数量引起的离散误差,本文选择4 种网格数进行网格无关性分析,结果如表1 所示。由表1可以发现,网格数14万时计算结果基本满足计算精度要求。因此,综合考虑计算时间和计算资源,本文决定采用14万网格数。
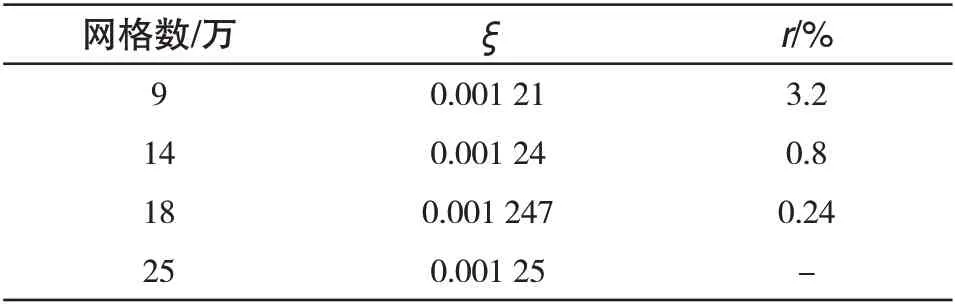
表1 网格无关性分析Tab.1 Grid independence analysis
3.2 叶片振幅对气动阻尼的影响
在叶轮阻尼及动应力未知的情况下,叶片的振幅是无法准确估计的。这里研究叶片振幅大小对气动阻尼的影响,考察了额定工况半开式离心叶轮前三阶模态的气动阻尼比,计算结果如图8 所示。对于同一模态,在不同振幅下,叶片的气动阻尼比基本保持不变,相关文献也得到了类似结果[16-18]。Bidkar[18]引进了一个无量纲量KC:

其中,A是振幅;c是结构特征长度。
当KC 值远小于1 时,气动阻尼比几乎与振幅无关。对于离心压缩机叶轮而言,振幅A 的范围在10-5~10-3m,特征长度c的范围在10-1~1m,KC值远小于1。因此,在同一工况某模态下叶片气动阻尼比可近似为常数。

图8 前三阶模态不同振幅下的叶片气动阻尼比Fig.8 Aerodynamic damping ratio for different modes
3.3 进口气体流量及温度对气动阻尼的影响
在机组实际运行时,根据生产工艺需求,需要改变进口气体流量。为了研究流量对气动阻尼的影响,本文计算了不同流量下叶片一阶模态的气动阻尼比,结果如图9所示。
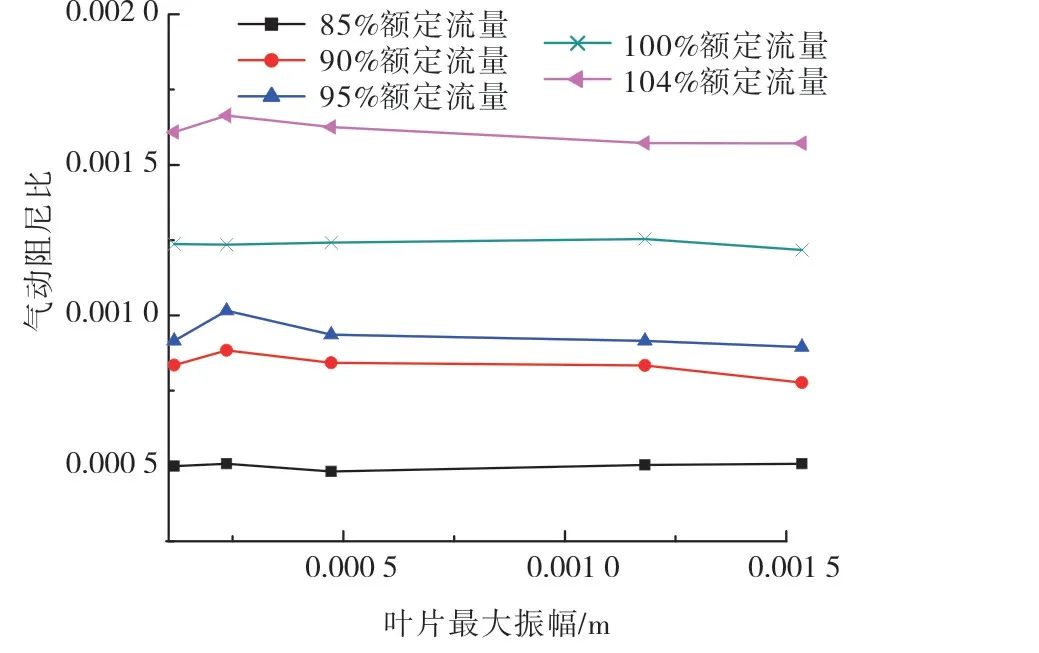
图9 不同流量下的叶片气动阻尼比Fig.9 Aerodynamic damping ratio for different flow rate
可以发现,同一模态同一工况下,不同叶片振幅下的叶片气动阻尼比基本不变。表2是不同流量下,取了各振幅的气动阻尼比平均值。可以发现,随着进口流量的增加,叶片气动阻尼比显著增大。

表2 不同流量下的平均气动阻尼比Tab.2 Average aerodynamic damping ratio for different flow rate
从压缩机运行特性方面分析流量对气动阻尼的影响规律。离心压缩机轴功率随进口气体流量的增大而增大,功率可表示为

其中,T0为作用在叶片上的扭矩;ω0为角频率。转速不变的情况下,叶片上的扭矩随功率的增大而增大。而作用在叶片上的扭矩由叶片表面的压力差决定。因此,气体流量的增大会使得叶片表面压差(压力载荷)增大。
如图11 和图12 所示是不同流量下,0.5 和0.9 倍叶高处(见图10)的压力面与吸力面气动压力差沿流线的分布(叶片一个振动周期内的平均值)。可以发现,流量增大时,叶片表面压差增大。因此,由式(1)可知,气动阻尼耗功增大,即气动阻尼比随流量的增大而增大。对于本文研究的半开式离心叶轮,进口质量流量由85%额定流量变化到104%额定流量,气动阻尼比由0.000 50变为0.001 61,增大了2.22倍。

图10 叶轮叶片子午流道Fig.10 Meridional view of blade
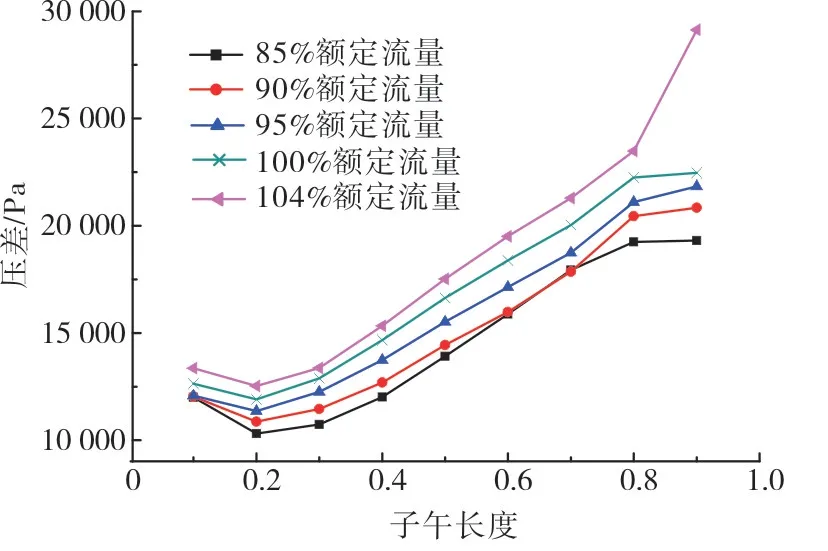
图11 0.5倍叶高处叶片表面的压差Fig.11 Pressure difference of blade surface at 0.5 blade height

图12 0.9倍叶高处叶片表面的压差Fig.12 Pressure difference of blade surface at 0.9 blade height
最后,考察气体进口温度对气动阻尼的影响。由于压缩机进口气体参数为当地大气参数,进口气体温度随环境的变化而变化,不是恒定值。因此,本文研究了两种工况下的气动阻尼结果。这两种工况包括夏季工况,进口温度为25℃;冬季工况,进口温度为-10℃。由于进口压力的变化相对较小,本文忽略压力对计算结果的影响,即两种工况下的进口总压取值都为99 000Pa。
压缩机运行工况的相似条件为:
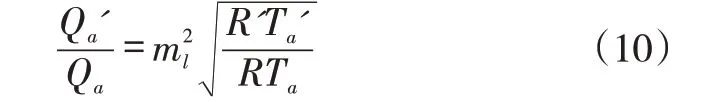
其中,Qa,Qa' 为两种工况下的进口气体体积流量;ml为叶轮结构几何比例;R' ,R 为气体常数;Ta' ,Ta为进口气体温度。对于同一台机组,ml=1;对于同一种气体,R' =R。因此,冬季工况下,进口体积流量为
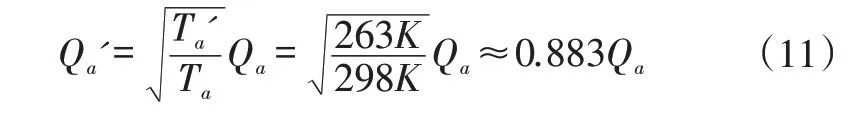
图13 是95%~104%额定流量下的气动阻尼计算结果。冬季工况与夏季工况计算结果类似,气动阻尼比随着进口流量的增大而增大。流量由95%额定流量增大到104%额定流量,气动阻尼比增大了86.1%。

表3 不同进口气体温度下叶片的气动阻尼比Tab.3 The aerodynamic damping ratio for different inlet air temperature
4 结论

图13 冬季工况下不同流量的气动阻尼比Fig.13 Aerodynamic damping ratio for different flow rate in winter
对于本文研究的半开式离心叶轮,冬季工况下,进口流量为额定流量的90%时,数值计算不能收敛。这是由于在冬季工况下,进口气体温度较低,密度较大,质量流量一定的情况下,体积流量减小。机组在冬季变工况运行,如果进口体积流量进一步减小,机组很可能进入非稳定流动状态,甚至发生喘振。此时,数值计算得到的流场也是非稳定的,无法得到一个恒定的气动阻尼值。
最后,由表3可知,额定流量下,对于叶轮的一阶模态,夏季工况(进口气体温度为25℃)和冬季工况(进口气体温度为-10℃)叶片的气动阻尼比分别为0.001 24和0.003 03,冬季工况叶片的气动阻尼比夏季工况增大了1.46倍。
本文研究了某半开式离心叶轮的气动阻尼特性,并且对气动阻尼的影响因素进行了理论分析。流固弱耦合计算可以使固体域与流体域分别建模,通过线性插值完成位移载荷的传递,从而使计算大大简化,实现任意固有频率及不同流场状态下的气动阻尼的计算。
分析发现叶轮在同一工况同一模态下的气动阻尼比与叶片振幅基本无关。数值计算结果表明,进口气体温度一定时,叶轮气动阻尼比随流量的增大而增大;而质量流量一定时,叶轮气动阻尼比随进口气体温度的减小而增大。因此,在设计中需要考虑变工况对气动阻尼的影响。
半开式叶轮的总阻尼包括气动阻尼和材料阻尼两部分,本文只对气动阻尼特性进行了初步研究,需要进一步综合考虑气动阻尼和材料阻尼的共同作用,才能获得准确的动应力计算结果。
