基于单神经元PID的采煤机滚筒调高控制系统

2021-03-24候德安

煤矿机电 2021年1期

候德安

(山西焦煤集团西山煤电屯兰煤矿，山西太原 030052)

0 引言

由于地下煤层的地质赋存条件复杂，回采过程中，沿倾向的煤层厚度、倾角等存在较大变化，因此，为防止采煤机滚筒截割到煤岩，同时最大化采收当前位置煤炭资源，应依据煤层厚度等因素及时调整采煤机前后滚筒的高度。采煤机司机可采用人工调整方式，但这种方法对工作人员的经验和操作准确性都有较高要求，随着煤炭开采自动化技术的发展，滚筒自动调高控制技术已得到广泛应用。

由于工作面实际工况的复杂性，采煤机自动调高控制系统具有显著的时变性和非线性特点，为提高控制过程的稳定性，一般采用PID闭环反馈算法进行优化控制。常规PID控制结构简单，易于实践，但其控制参数仍依赖于人为经验设定，对于较为复杂的采煤机调高控制，可能因参数设置不当而出现控制不稳定现象[1-3]，因此仍需寻找一种效率更高和更稳定的滚筒调高闭环控制方法，本文将对此进行研究。

1 采煤机滚筒调高系统组成

如图1所示，采煤机滚筒调高系统主要由液压控制系统、电气控制系统、检测装置和机械执行机构等组成。其中，液压控制系统包括电液比例换向阀、泵、电动机、安全阀、液压锁等，电气控制系统包括控制器(具有PID算法功能)、D/A转换器、功率放大器等，检测装置采用线性传感器，机械执行机构则包括调高油缸、摆臂等[4-6]。

图1 采煤机滚筒调高系统

滚筒调高控制过程如下：控制器接收外部调整指令，经过D/A转换，将数字控制信号放大后作用在电液比例阀相应位置的电磁铁上，控制阀芯按指定数值位移，然后液压泵将高压乳化液注入阀芯移动后形成的液压管路，并进入调高油缸的相应腔体内，控制油缸杆伸出或缩回，滚筒高度相应调整，同时，油缸内的线性传感器将位移信号传回电气控制系统，经A/D转换后进入控制器，控制器将实际位移信号与输入位移指令进行对比，得出位移偏差，然后经过PID处理后再次输出控制信号，阀芯微动，滚筒位置做出微调，上述过程呈动态进行，由此可保证滚筒调高过程的自动化和稳定性。

2 闭环控制系统数学模型

2.1 控制原理

若要对控制系统的特性进行分析，应首先绘制控制原理图。滚筒调高控制系统的控制过程及原理如图2所示，在此基础上，需进一步建立方框内各控制元件的传递函数，以便后续建模计算和分析。

图2 滚筒调高系统控制过程及原理

2.2 传递函数模型

2.2.1 功率放大器

由于控制器输出功率较小，因此需通过功率放大器将输出的电压信号按比例放大为电流信号，特定大小的电流作用在电液比例阀的电磁铁上产生磁力，并控制阀芯按比例位移值移动。由于该环节主要是通过比例运算进行功率放大，因此其传递函数表示如下：

G1=Km

(1)

式中,Km为功率放大系数，取Km=0.75 A/V。

2.2.2 电液比例换向阀

相比于调高液压缸，电液比例换向阀的响应速度更快，频率更高，其在控制系统中的作用类似于比例环节，因此该元件的传递函数如下：

G2=Ksv

(2)

式中,Ksv为比例阀增益系数，取Ksv=0.89×10-3m3(s·A)-1。

2.2.3 阀控调高液压缸

阀控非对称调高液压缸是控制系统的重要组成部分，假设系统供液的压力、温度、密度均恒定不变，回液压力为零，且换向阀的阀口为紊流，液压缸各处泄漏为层流，则该部分的传递函数表示如下：

(3)

式中:Kq为流量增益系数，Kq=1.6×103L/(s·m)；Xv为换向阀阀芯位移值，Xv=0.01 m；Kce为总流量系数，取Kce=7.96×10-11m5/(N·s)-1；Am为非对称液压缸两腔的平均面积，Am=21.7×10-3m2；A1为非对称液压缸无杆腔面积，A1=25.4×10-3m2；Vt为液压缸的等效容积，Vt=6.10×10-3m3；βe为压力介质的体积弹性模量，取βe=7×108N/m2；FL为外负载力，FL=2×105N；Wh为液压缸的固有频率，Wh=194.9 r/s；ξh为液压缸的阻尼比，取ξh=0.2。

2.2.4 位移传感器

位移传感器安装在液压缸活塞尾部，一般采用磁致伸缩式，可将活塞的位移信号转化输出为电压信号，其响应速度较快，可简化处理为比例环节，传递函数表示如下：

G4=Kf

(4)

式中，Kf为传感器增益，取Kf=40 V/m。

2.2.5 PID控制器

当前PID控制算法种类较多，相应传递函数也不相同，功能差异较大，以常规PID算法为例，其传递函数如式(5)所示，式中Kp、Ti、Td3个参数一般需根据经验进行设定。

(5)

式中:Kp为常规PID算法的比例常数，取Kp=0.6；Ti、Td分别为积分和微分常数，取Ti=0.9、Td=0.8。

2.3 控制系统传递函数

采煤机调高控制系统的传递函数框图如图3所示。

图3 调高控制系统传递函数框图

3 单神经元PID优化算法

常规PID算法可满足一般线性控制系统要求，但对于滚筒调高控制，其系统非线性、时变性特点明显，且外负载扰动较大，因此常规PID算法的参数取值尤为困难，实际的控制精度和性能已无法满足现代采煤工艺要求。神经元算法是近年来工业应用较多的优化算法，可实现在线模型参数自学习、自适应等功能，从而适应复杂系统的精确控制。单神经元PID优化算法将神经元法和常规PID算法相结合，可对常规PID算法中的Kp、Ti、Td3个参数进行在线自适应调整，提高系统响应速度和适应能力。

单神经元PID优化算法的控制原理如图4所示，其中W1(k)、W2(k)、W3(k)为神经元权值，对应常规算法的Kp、Ti、Td3个参数，控制偏差e(k)是单神经元PID算法的输入信号，令X1(k)=e(k)-e(k-1),X2(k)=e(k),X3(k)=e(k)-2e(k-1)+e(k-2)，则该PID算法的输出信号为：

(6)

式中:k为反馈循环次数；K为神经元的比例系数，取K=0.2，K对系统较为敏感，K越大，系统响应越快，超调量增大；K越小，系统响应越慢，超调量减小。

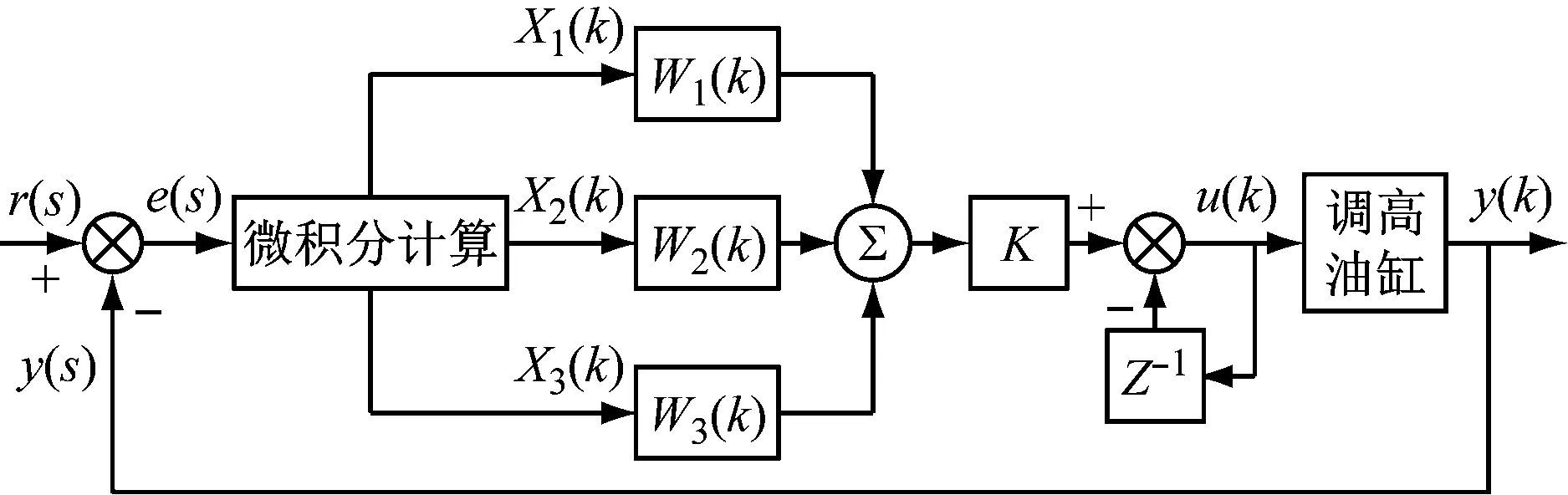
图4 单神经元PID优化算法控制原理

4 基于数学模型的仿真分析

4.1 仿真模型

根据上述研究结果，利用MATLAB/Simulink软件分别建立基于常规PID算法和单神经元PID优化算法的滚筒调高控制系统模型，其中，单神经元PID优化算法仿真模型如图5所示。

(a) 优化算法总模型

4.2 仿真结果分析

4.2.1 系统响应

为对比两种算法对系统响应的影响，分别给定相同的目标阶跃信号和外负载扰动，仿真时间10 s，调高油缸位移响应曲线如图6所示。由图6可见,单神经元PID算法的响应速度更快，约1.6 s即达到系统稳定，超调量也更小，最大超调量为0.11 mm；而常规PID算法的响应速度为4.2 s,超调量为0.23 mm。由此可知，通过合理设置单神经元PID算法的相关参数，可使其控制系统的响应速度加快、稳定性增强。

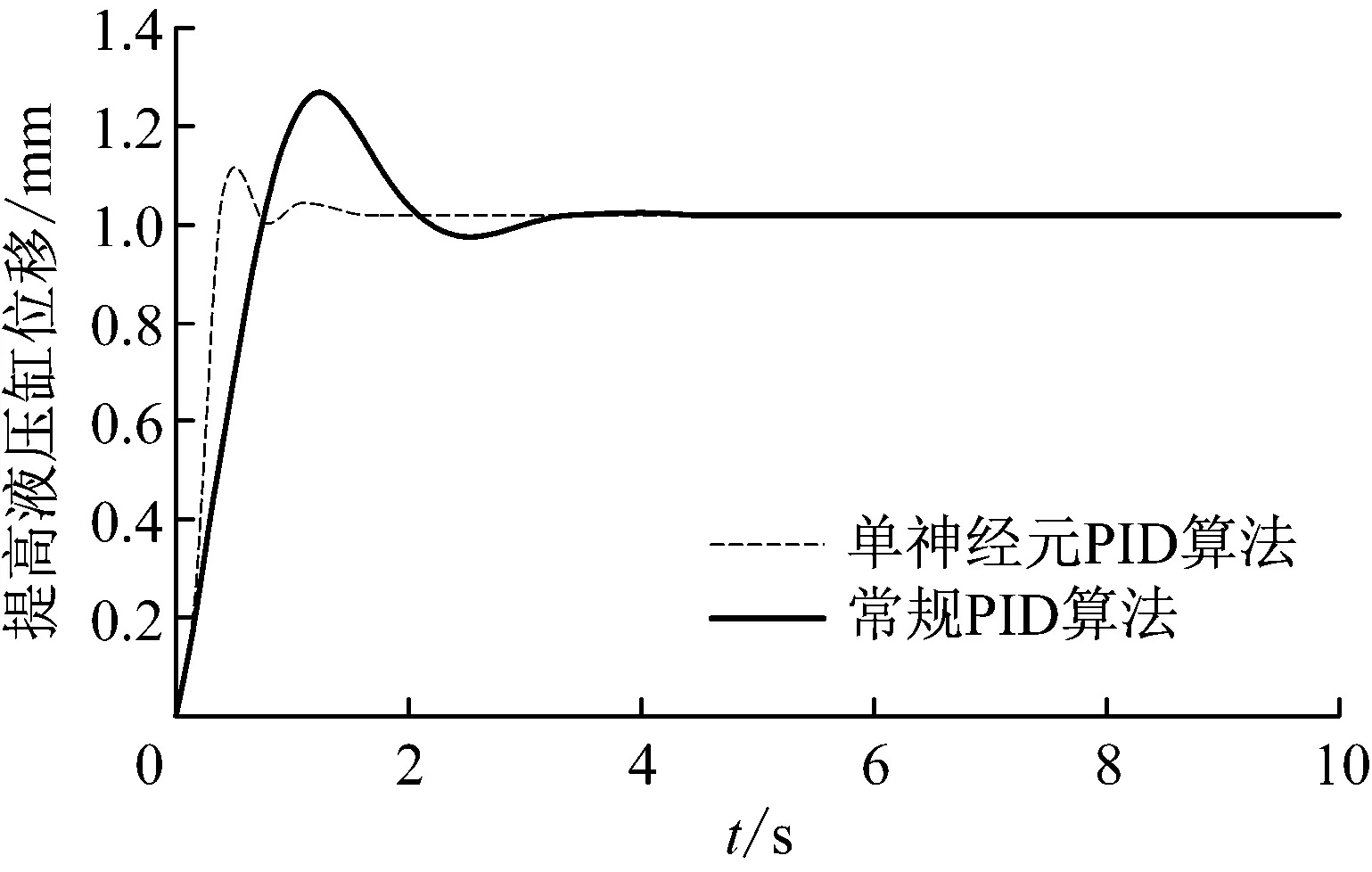
图6 不同PID算法对系统响应的影响

4.2.2 抗负载扰动能力

为对比两种算法在外负载扰动下的抗干扰能力，在上述阶跃信号的基础上，在6 s时将外负载由200 kN突变至400 kN，响应曲线如图7所示。由图7可见,单神经元PID算法可在1.5 s内快速恢复稳定，且波动幅度较小，而常规PID算法的平衡时间达到2.3 s，因此说明单神经元PID算法对负载较大扰动工况有良好的适应性。