通用脉冲雷达信号仿真软件设计与实现*

张华杰

（新乡学院物理与电子工程学院，河南 新乡 453000）

0 引言

雷达系统在军事和民用领域都有着很广泛的影响，长期以来我国的雷达制造水平有了长足的发展，但在系统的仿真领域起步较晚，而且缺乏统一的规划。随着雷达系统的日益复杂，进行雷达系统软件仿真的难度也越来越大，软件系统的规模和复杂性也日益增加。

雷达信号仿真系统的设计与实现是雷达信号理论工程实现的重要途径之一，雷达系统仿真就是通过建立雷达系统模型，利用软件和硬件的手段复现雷达系统的动态工作过程。它仿真的对象是雷达系统，包括雷达本身（硬件及软件），雷达回波和回波环境；仿真的方式是复现蕴含雷达回波场景信息的雷达回波信号及其传递、处理的动态过程，从时间关系上看，就是重现一个随机的时间序列。由于雷达发射波形不仅决定了信号处理方法，而且直接影响系统的分辨力、测量精度以及抑制杂波能力等潜在性质。于是，波形设计就成了雷达系统最佳综合的重要内容，逐渐形成现代雷达理论的重要分支。综上所述，雷达信号理论的形成与发展，目的在于提高雷达信号传输的可靠性和有效性。

1 典型雷达的脉冲信号

将幅度A 归一化为1，得到单载频矩形脉冲信号的模糊函数表达式

以上三式可合并为

取模得到

线性调频矩形信号表示为

线性调频矩形脉冲信号，其载频在脉冲宽度内按线性规律变化，即用对载频进行线性调制的方法展宽信号的频谱，使其相位具有色散特性。同时，在发射信号的峰值功率Pi受限的情况下，为了充分利用发射机的功率，通常采用矩形宽脉冲的信号包络。

其中，调频带宽

Δf 成为调制频偏。用对应的角频率表示可以写为ΔΩ=2πΔf，故调频斜率为

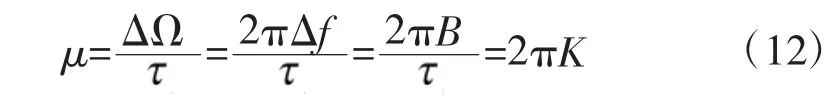
若信号的载波中心角频率为Ω0=2πf0，则线性调频矩形脉冲信号的角频率变化规律为

因而，信号的瞬时相位φ（t）为

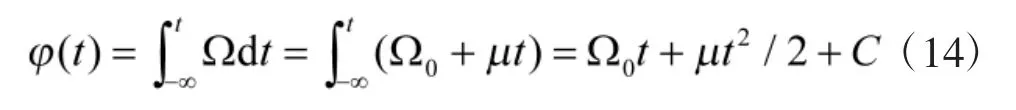
这样，线性调频矩形脉冲信号的表达式为

其中，μ=2πK。为了方便计算分析，将信号s（t）用复数形式表示为

对信号s（t）进行傅里叶变换，得信号的复频谱函数为

则信号的频谱函数表达式为

1.1 幅频函数及特性

线性调频矩形脉冲信号的幅频函数为

当f=f0时，可得

当D>>1 时，有c（v1）=c（v2）≈0.5，s（v1）=s（v2）≈0.5

所以，可得幅频函数为

当f=f0+Δf/2 时，可得v1= 2D ，v2=0

当D>>1 时，有c（v1）=c（v2）≈0.5，s（v1）=s（v2）≈0

可得，（22）

即幅度频谱为中心角频率f=f0时的一半。

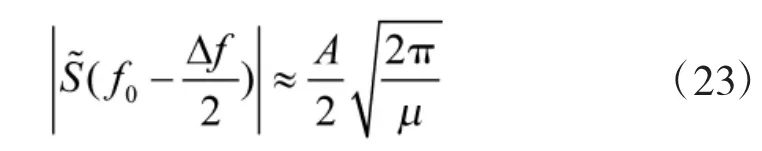
即幅度频谱也为中心角频率f=f0时的一半。

当压缩比D 不同时，幅度频谱的特性也随之变化。D 值越大，则幅频特性在（f0-Δf/2）～（f0+Δf/2）之间越平坦，在这个频带之外幅度下降越快，信号的能量主要集中在此频带范围内。计算结果表明，当D=10 时，则95%的信号能量包含在此频带范围内；当D=100 时，则98%的信号能量包含在此频带范围内。由于实际使用的线性调频矩形脉冲信号通常均满足D=B>>1，故其幅频特性很接近矩形，所以可近似表示为，

1.2 相频函数及特性

线性调频矩形脉冲信号的幅频函数为

它包含平方相位项和剩余相位项两部分，反映了信号的相频特性。

其中，平方相位项为

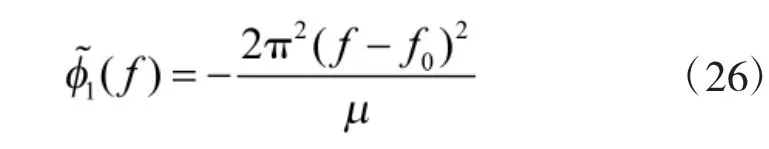
剩余相位项为

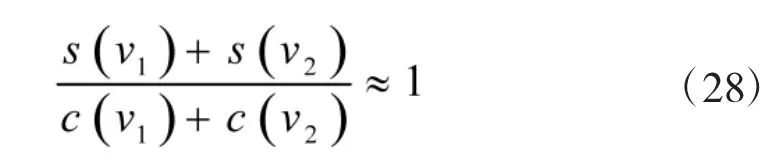
因而

当D>>1 时，线性调频矩形脉冲信号的相频函数可近似表达为

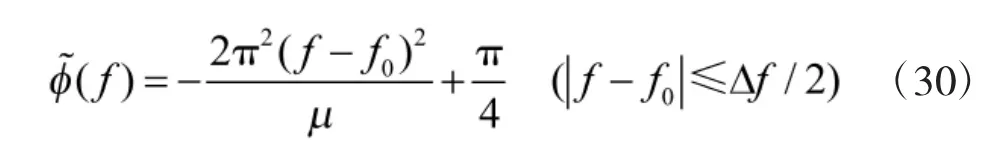
这样，当压缩比D 很大时，线性调频矩形脉冲信号的相频函数可表示为

综上讨论，线性调频矩形脉冲信号具有如下主要特点：

2）线性调频矩形脉冲信号具有近似矩形的幅频特性，D 值越大，其幅频特性越接近矩形，频谱宽度近似等于信号的调频宽度B=Δf。

3）线性调频矩形脉冲信号具有平方律的相频特性，在设计匹配压缩滤波器时要考虑到相位频谱函数的这一特性。

将线性调频矩形脉冲信号的幅度A 归一化为1。根据模糊函数的性质4，时域引入平方相位项对模糊函数的影响，线性调频矩形脉冲信号的模糊函数可由单载频矩形脉冲信号函数按下列关系

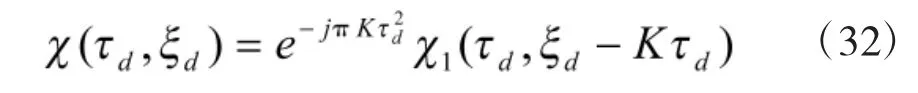
直接导出。可得

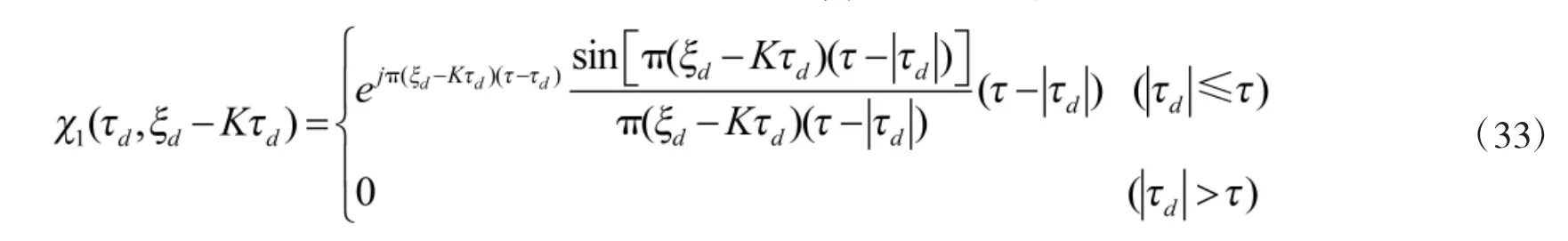
于是得到

取模得到

伪随机二相编码信号的复包络为

伪随机二相编码信号的表达式为

伪随机相位编码信号的复信号表示为

式中，φ（t）为相位调制函数。

对二项编码信号来说，φ（t）只取0、π 两个数值，可用二进制相位序列{φk=0、π}表示，也可用二进制数字序列{ck=ejφk}=±1 表示。如果二相编码信号的包络为矩形，即

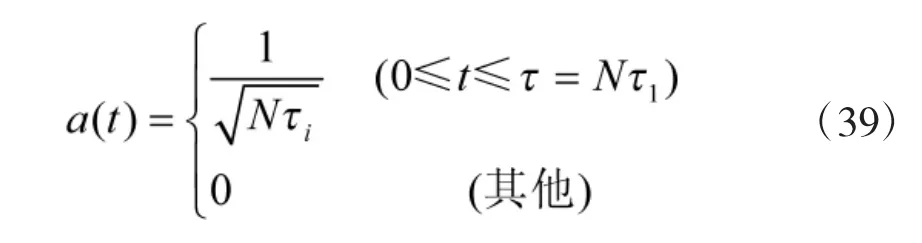
则二相编码信号的复包络可写成

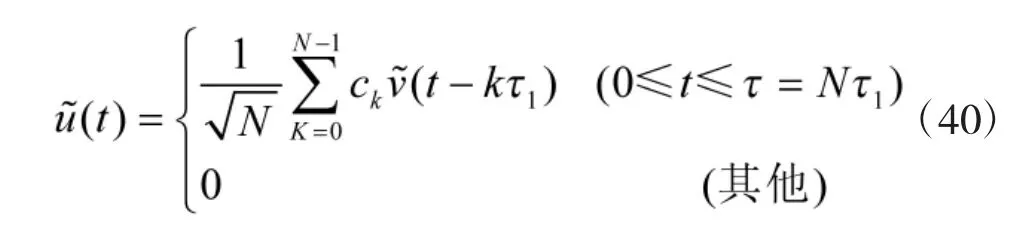
应用傅里叶变换对

和傅里叶变换的性质，可得

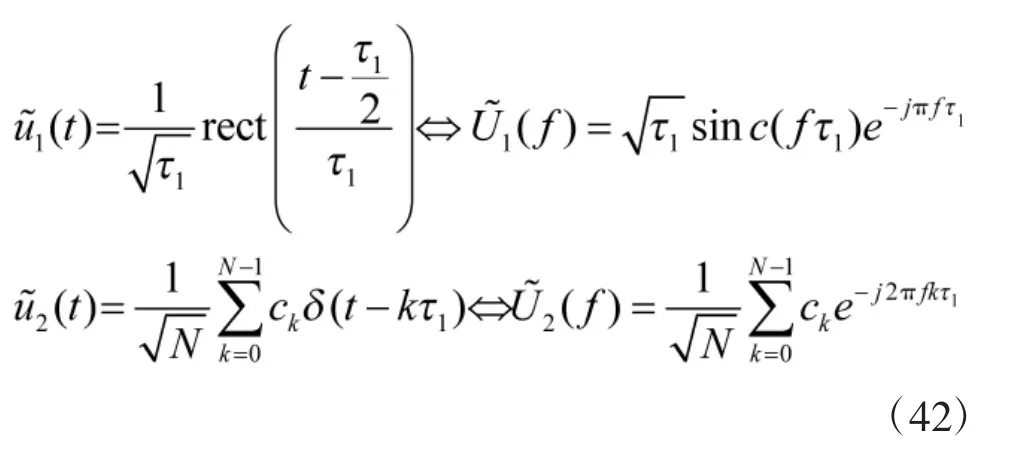
由傅里叶变换的时域卷积定理，得伪随机二相编码信号的频谱函数为

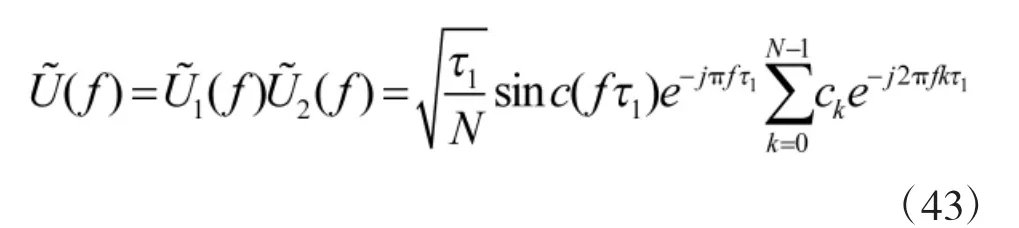
式中

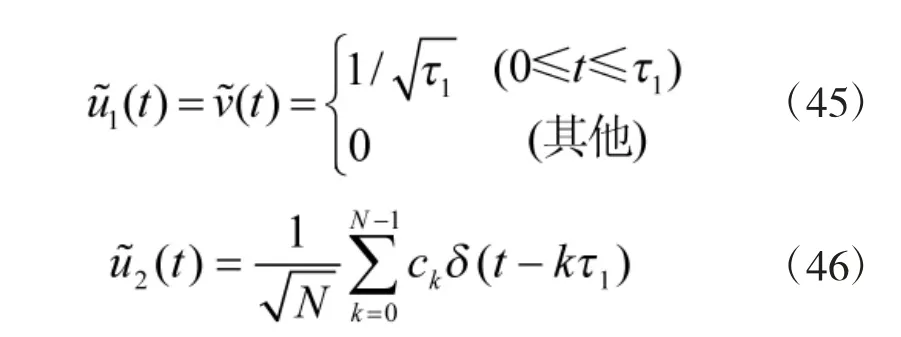
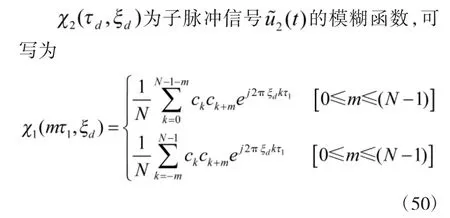
伪随机二相编码信号的模糊函数，就是它的复合自相关函数，根据定义为

利用线性卷积的运算性质，得伪随机二相编码信号的模糊函数为

2 仿真软件的结构与功能

通用雷达信号仿真软件可以简便快速地获得各种载波频率，脉冲宽度等数据的单载频矩形脉冲信号、线性调频矩形脉冲信号和伪随机二相编码信号的数据、波形、频谱，包括模糊函数。

从而，在学习的过程中，学员能够直观形象地学习和理解各种雷达脉冲信号，同时对于相关的科研工作，能够提供所需的各种雷达信号数据，为雷达信号处理相关算法研究提供数据支撑。

为了实现上述功能，设计了通用脉冲雷达信号仿真软件，如图1 所示为设计仿真软件的结构图。

图1 仿真软件结构图

其中，左上部分是3 种典型雷达信号的脉冲信号选择，包含了单载频矩形脉冲信号，线性调频矩形脉冲信号以及伪随机二相编码信号。

左下是各种雷达信号参数的设置，包括载波频率、脉冲宽度、脉冲重复间隔、信号幅度、初始相位、信噪比、起始频率、调制带宽、采样频率和采样时间。

右侧是仿真所得到的4 种结果图，分别为信号幅度-采样时间图、信号幅度-采样点数图、信号频谱图以及模糊函数图。通过此软件即可实现对雷达信号的波形，复包络，频谱，以及模糊函数的提取。

参数设置如下：

载波频率：3 MHz，脉冲宽度：75 us，脉冲重复间隔：300 us，信号幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始频率：3 MHz，调制带宽：1 MHz，采样频率：20 MHz，采样时间：5 ms。

图2 单载频矩形脉冲信号时域描述图

通过观察图2，可得到脉冲宽度为75 us，脉冲重复间隔为300 us，符合参数设置。

图3 单载频矩形脉冲信号单个脉冲图

通过观察图3、下页图4，可得到载波频率为3 MHz，调制带宽为1 MHz，符合参数设置。

通过观察图5，可得到单载频矩形脉冲信号的模糊函数图为正刀刃型，符合该信号模糊函数的特点。

图4 单载频矩形脉冲信号频谱图

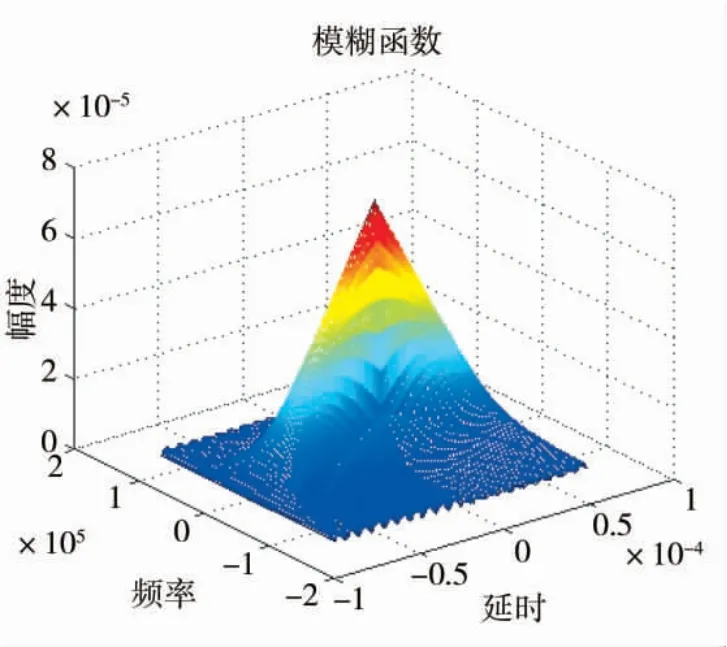
图5 单载频矩形脉冲信号模糊函数图

参数设置如下：

载波频率：10 MHz，脉冲宽度：25 us，脉冲重复间隔：200 us，信号幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始频率：10 MHz，调制带宽：1 MHz，采样频率：50 MHz，采样时间：5 ms。

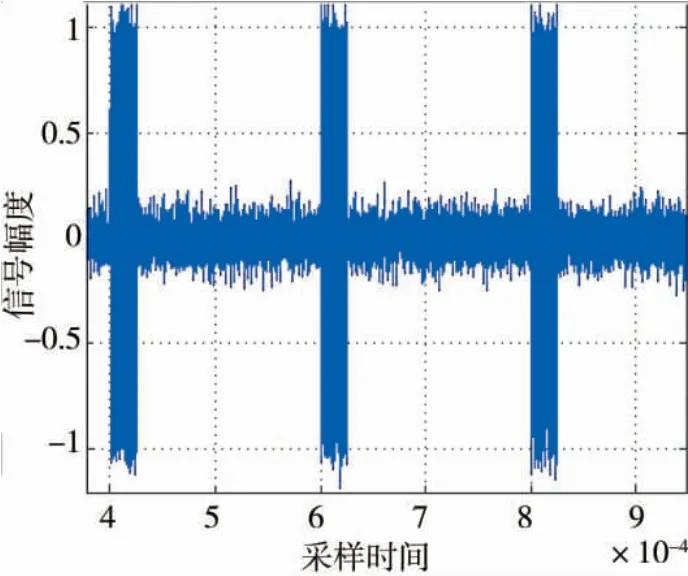
图6 线性调频矩形脉冲信号时域描述图

通过观察图6，可得到脉冲宽度为25 us，脉冲重复间隔为200 us，符合参数设置。

通过观察图7、图8，可得到载波频率为10 MHz，调制带宽为1 MHz，符合参数设置。

通过观察图9，可得到单载频矩形脉冲信号的模糊函数图为斜刀刃型，符合该信号模糊函数的特点。

参数设置如下：

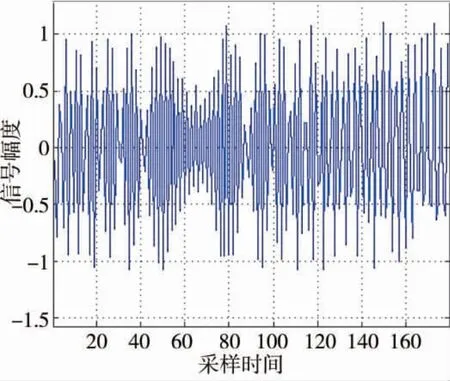
图7 线性调频矩形脉冲信号单个脉冲图

图8 线性调频矩形脉冲信号频谱

图9 线性调频矩形脉冲信号模糊函数图

载波频率：5 MHz，脉冲宽度：50 us，脉冲重复间隔：300 us，信号幅度：1 V，初始相位：0 rad，信噪比：20 dB，起始频率：5 MHz，调制带宽：1 MHz，采样频率：20 MHz，采样时间：5 ms。

通过观察下页图10，可得到脉冲宽度为50 us，脉冲重复间隔为300 us，符合参数设置。

通过观察图11、图12，可得到载波频率为5 MHz，调制带宽为1 MHz，符合参数设置。

通过观察图13，可得到单载频矩形脉冲信号的模糊函数图为钉型，符合该信号模糊函数的特点。

3 结论

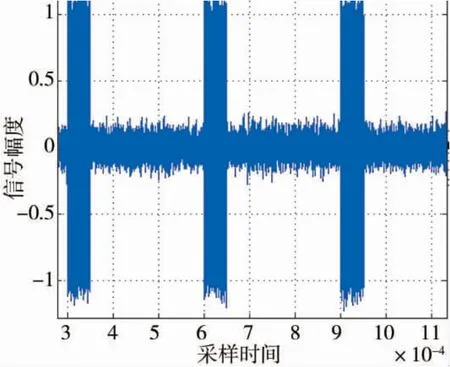
图10 伪随机二相编码信号时域描述图

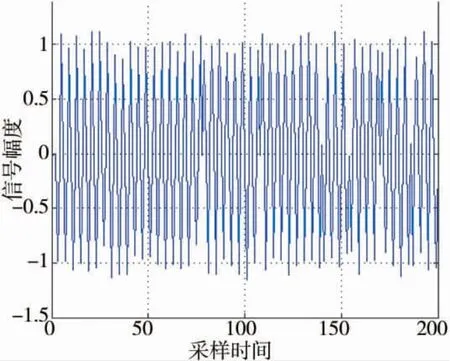
图11 伪随机二相编码信号单个脉冲图

图12 伪随机二相编码信号频谱图

图13 伪随机二相编码信号模糊函数图

本文以雷达信号的基本理论为引子，从雷达信号的时域表示、频域表示以及模糊函数开始入手，阅读搜集了大量雷达信号理论方面的资料，归纳总结了3 种典型的雷达脉冲信号的复包络、时域描述、频谱函数、模糊函数及其特点，以此为基础建立了3 种雷达脉冲信号的完整的数学模型，最后，基于Matlab 仿真软件对3 种典型的雷达脉冲信号进行了仿真实现，设计并编写了通用雷达脉冲信号仿真软件。通过对比试验结果图，发现与理论分析是一致的。

通用脉冲雷达信号仿真软件的实现，不但解决了军校学员在学习雷达理论时无法很好地理解相关知识的难题，还能够为相关的科研工作提供所需的各种雷达信号数据，完成雷达信号处理相关算法研究。

但是，在本次研究设计中，仅仅完成了3 种典型雷达脉冲信号的仿真设计，在繁复的雷达种类中，要想更好地获取相关实验数据，如信号复包络、模糊图等，仍缺少相应的手段。因此，在下一步工作中，会针对其他的各种复杂雷达信号进行学习分析，并努力归纳整理出相关的理论，逐步地完成更加复杂的雷达信号的仿真设计与实现。