基于多源传感器的单星定位算法与精度分析

邓彦鑫，郭 伟，李柯陶

（中国航空无线电电子研究所，上海 200241）

0 引言

全球导航卫星系统（Global Navigation Satellite Systems，GNSS）凭借其高精度、应用便捷、覆盖范围广且全天候全天时服务等诸多优势成为目前性价比最高、应用领域最广的定位导航授时系统［1］。但其存在一个重大的问题，就是卫星信号的羸弱性。卫星信号从几万公里的太空传到地球表面，信号极易受到干扰，遮蔽和欺骗。当卫星信号由于受到建筑物，山体等遮挡而导致接收机接收到的卫星空间分布不好甚至卫星数少于4 颗时，卫星导航接收机将无法提供实时定位。或在极端战争时期，GNSS 可被各式反卫星技术轻易破坏或摧毁而失效，应急响应发射备用卫星时，往往很难同时发射4 颗及以上数量的卫星并完成快速组网提供服务。此外卫星空间载荷异常、地面控制端出现故障等也可能造成GNSS 的定位，导航和授时（Positioning，Navigation and Timing，PNT）服务中断。因此，实现可见卫星数目不足时的应急定位至关重要，国内外的诸多学者针对该问题，提出采用单星定位系统作为卫星导航星座拒止服务环境下的应急响应系统，采用大椭圆轨道并在轨道远地点为用户提供定位服务，以满足长时间服务的要求，而在近地点卫星会快速通过非服务区［2］。对国内外近些年已公开的文献分析可知，这种定位方法卫星的定轨精度较低，所以定位误差较大，仅凭单颗卫星的测量信息是无法完成高精度的定位功能，其定位精度总会受到相关因素的制约［3-8］。因此，需要考虑加入高精度外部传感器的方式辅助定位。

本文在假设接收机只获得一颗卫星信号的极端条件下，分析利用多源传感器信息辅助单星定位的可行性，提出了基于多源传感器信息的单星定位算法。通过添加高精度气压高度计提供系统高度信息以及芯片级原子钟（Chip Scale Atomic Clock，CSAC）消除接收机时钟钟差的方法，增加卫星定位测距算法中的辅助方程，从而实现使用更少时刻的卫星数据提供定位服务，最终解决单星定位过程中由于卫星空间分布差造成定位精度低的问题。通过理论分析、数字仿真实验和静态试验的方法，对提出的算法精度和有效性进行了分析和验证。

1 定位方法

1.1 定位原理

多源传感器信息辅助下的单星连续测距定位原理如图1 所示。即假设用户静止不动，接收机持续观测收集不同时刻t 卫星的伪距测量值，以及各项偏差、误差成分的校正量（卫星部分误差校正量）、I（t电离层延时校正量）、T（t对流层延时校正量）和（多路径误差校正量）等，从而获得各时刻校正后的卫星伪距观测值，以及各时刻由卫星星历计算并经地球自转校正后的卫星位置坐标。

由于利用CSAC 代替TCXO 作为接收机内部时钟，可认为由接收机时钟误差造成的伪距测量误差（厘米级）可忽略不计。

图1 单星连续测距定位原理图

假设未知用户的位置坐标为（x，y，z），根据t1、t2到tn这n 个时刻的伪距测量值可建立如下非线性方程组：

在接收机的三维位置坐标经度、纬度和高度中，通常高度信息可通过外部辅助设备（如气压高度计、电子地图等）测定，或在一个区域内可认为高度值固定已知，此时只需求解接收机在水平方向上的二维位置坐标分量，便可精确获得接收机的位置。同时减少未知数的求解可增加定位时的信息冗余度，从而提高接收机在水平方向的定位精度。

具体到方程组的求解时，虽然已知用户的高度值，但该高度是指地球坐标系g系中运载体的高度h，而在地心地固坐标系e 系中运载体的三维坐标（x，y，z）仍均为未知数，因此，不能通过直接减少一个未知数来完成定位求解，而是增加辅助方程个数，即建立高度与运载体三维坐标间的关系式并添加到定位方程组中使得系统只需观测两个时刻的卫星数据便可完成定位解算。

用户高度h 与其三维位置坐标（x，y，z）之间的关系式如下：其中，Re、Rp和RN分别为地球的长半轴、短半轴和运载体所在地的卯酉圈曲率半径。简化计算可得用户的高度曲面方程

其中，e 为地球偏心率。

与传统定位方法相比，单星连续测距定位采用“以时间换空间”的原理，利用卫星随时间在空间几何位置的变化弥补了系统的可观测性，为系统提供了足够的量测信息用于求解方程组，采样时间间隔越长，卫星不同时刻间的位置几何分布越好，定位精度越高。同时该方法利用了CSAC 的高精度授时功能，降低了定位时的测量维度，提高了系统的性能。

将式（3）加入到式（1）中组成基于多源传感器信息的单星定位方程组，采用最小二乘法进行求解，具体解算过程因篇幅原因不做赘述，可参考文献［10-11］。

1.2 精度分析

考虑接收机观测卫星并获得伪距过程中tn时刻的伪距测量误差，则由最小二乘法解得线性化矩阵

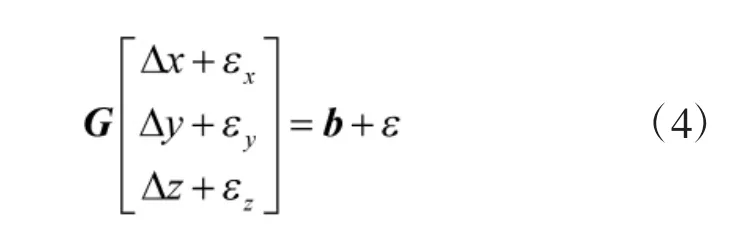
其中

式（6）表明了伪距测量误差与定位误差之间的关系，一般以均值和方差来描述测量误差对定位误差的影响大小，从简化定位精度理论分析考虑，我们做以下两点假设分别阐述。

则测量误差向量ε 的均值为

假设各时刻卫星测量之中伪距测量误差的各部分误差相互独立，则有

其中，σS代表由卫星时钟误差和卫星星历误差造成的伪距测量误差标准差，值约为3 m，σP代表卫星信号传播中电离层延时和对流层延时造成的伪距测量误差标准差，值约为5 m，σR代表与接收机和多路径有关的误差造成的伪距测量误差标准差，值约为1 m。计算可得伪距测量误差造成的定位误差约为5.9 m。实际中的估算方法要更复杂，包括考虑卫星信号强度，卫星仰角值和接收机跟踪环路运行状态等具体指标，这里不做深入探讨。

2）假设卫星各时刻间的测量误差不相关。

此时测量误差向量ε 的协方差矩阵Kε为

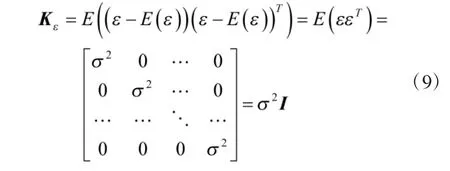
其中，I 为n×n 的单位阵。实际测量时，由于是接收同一颗卫星的发射信号，不同时刻间的测量误差间肯定存在相关性，此处假设只是为简化定位误差协方差矩阵的推导。则由式（6）和式（9）可得

采用几何精度因子GDOP 来表示误差的放大倍数，其计算方法为

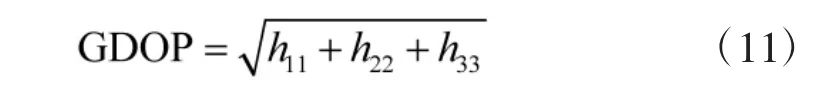
将定位误差从地心地固坐标系转化到地理坐标系中有

其中

为地心地固坐标系到地球坐标系的方向余弦矩阵。

则式（10）在地球坐标系下的表示为

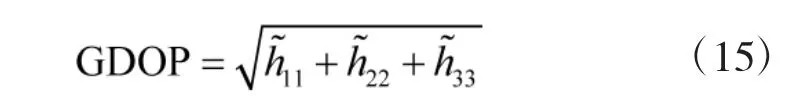
GDOP 值越小，定位误差越小。

将式（4）不考虑伪距测量误差投影到地球坐标系中有

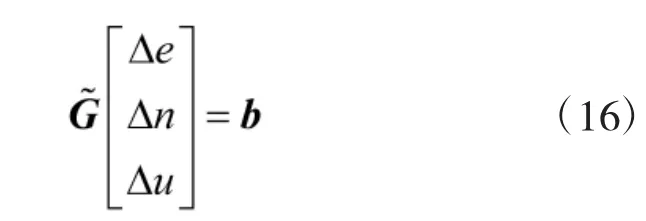
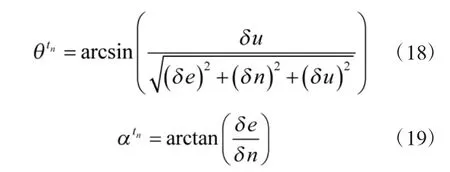
2 验证分析

为了验证所设计的基于多源传感器的单星定位算法的有效性和精度，本文采用数字仿真验证和跑车动态试验方式进行验证。1）数字仿真验证：通过仿真卫星的轨道实现卫星的仿真数据激励，模拟静态载体长时间只接收一颗卫星的星历数据，对不同数量传感器辅助下的单星定位算法进行了有效性仿真验证，采用蒙特卡洛分析法对算法的定位精度数据进行了统计分析；2）静态试验验证：利用GNSS 单频接收机、高精度气压高度计和CSAC 搭建基于C 多传感器的单星定位静态试验环境，完成对一颗卫星信号的持续观测，并利用所获得的试验数据对单星定位系统进行了精度评估，最终验证基于多源传感器信息的单星定位算法在实际应用时的有效性和精度。

2.1 数字仿真验证

利用自行设计的理想圆轨道卫星仿真软件，载入一颗编号为“4”的在轨卫星进行仿真数据激励，其卫星轨道特征如表1 所示。

选择卫星的过顶时间作为单星定位服务时间段，其运行时长为1 h，用户位置为（北纬34.25°，东经108.91°，高380 m），星下点轨迹如图2 所示。

由于短时间内卫星运行距离较短，导致不同时刻的卫星依然集中在一起或在一条直线上，这时不同时刻卫星的几何分布很差，因此，本试验选取t=300 s 时刻为起始解算时刻，即单星定位接收机开机前5 min 只做数据收集工作，从5 min 开始做定位解算，每个时刻t 选取3 个时刻的卫星信息作为伪距量测信息，这3 个时刻分别为1、t/2 和t 时刻，以确保卫星的几何分布结果最好。

表1 “4”号卫星轨道特征表

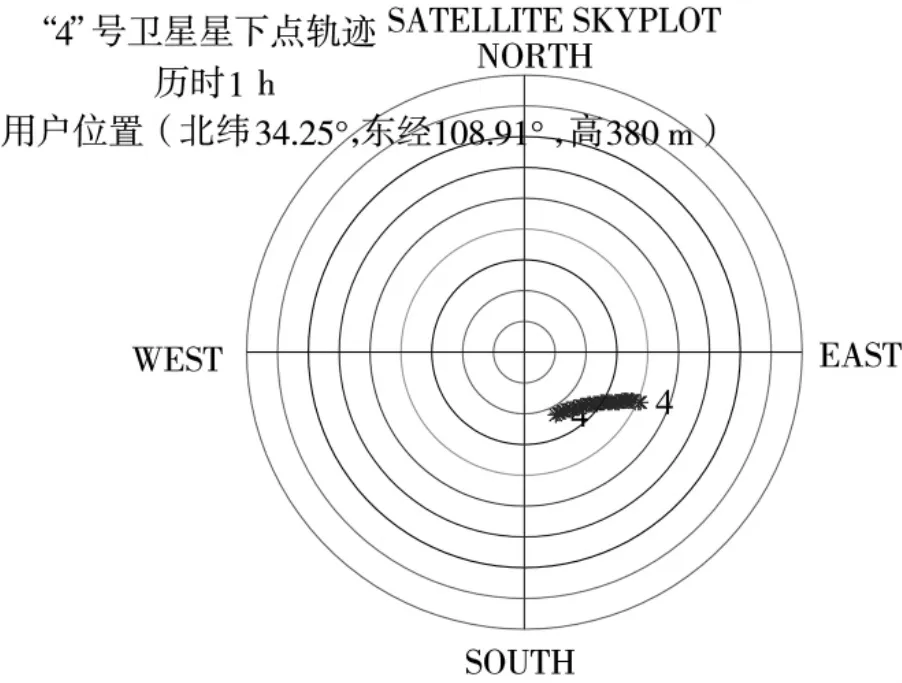
图2 “4”号卫星1 h 运行星下点轨迹图

分别选择注入伪距观测误差均方差为1 m 和3 m，在上述仿真环境下进行单星定位解算，根据上述仿真条件，其中当伪距观测误差均方差为1 m 时，得到用户的三维定位结果误差和几何精度因子GDOP 随时间的变化如图3、图4 所示（程序横坐标轴t 时刻为接收机开机后（t+300）s 时刻）。

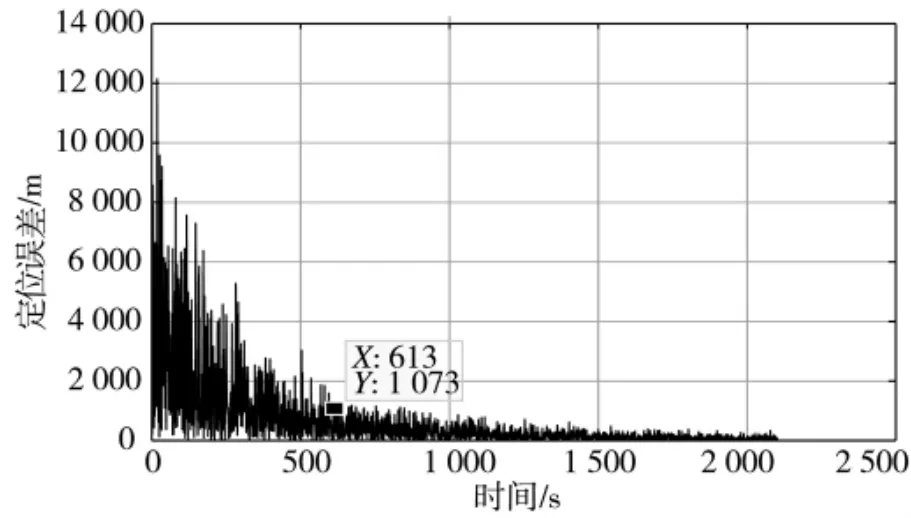
图3 伪距测量误差为1 m 时的单星定位结果

图4 伪距测量误差为1 m 时的GDOP

由图3 可知，当伪距测量误差均方差为1 m 时，仅以CSAC 辅助单星定位解算是可行的，仿真在900 s 左右完成了精度为1 km 的定位。由图4 可知，随着时间的增加，系统的GDOP 值在减小，即所选取3 个时刻的卫星的几何分布越来越好，但在900 s左右时GDOP 值仍在103的数量级别，这表明单星定位短期效果仍远差于传统的多星定位。

利用蒙特卡洛仿真分析单星定位精度的统计特性，分别对用户伪距测量误差均方差为1 m 和3 m，采样时间为600 s 和1 200 s 时的单星定位进行100 次蒙特卡洛仿真，求得其结果的RMS 误差作为单星定位统计精度，其中伪距误差为1 m，采样时间为1 200 s 时的蒙特卡洛仿真统计结果如图5 所示，总的仿真统计结果如表2 所示。

由表2 结果可知，基于CSAC 辅助的静态单星定位虽然可行，但由于仅能利用1 颗卫星的数据，多个时刻卫星的空间几何分布很差，导致GDOP 过大，当伪距测量误差的均方差为1 m 时，需持续观测20 min 方能达到400 m 的定位精度，而当伪距测量误差的均方差只增加2 m（从1 m 到3 m）时，最终定位精度便从365.926 m 上升到1 270.489 m，可见单星定位系统是及其脆弱的，即使利用CSAC 降低了一维的测量维度信息，最终定位结果仍随较小的伪距测量误差的变化发生较大的波动，其根本原因就是短时间测量得到的3 个时刻的3 个卫星位置之间的空间相关性很高，卫星的几何分布很差，从而使得权系矩阵H（或）的元素值过大。

图5 伪距测量误差为1 m 时的100 次蒙特卡洛仿真统计

表2 基于CSAC 的单星连续测距定位精度（RMS）

设置仿真条件同上，并只采用两个时刻（1 时刻与t 时刻）的卫星数据，假设用户高度信息h=380 m可通过外部辅助器件测量获得。考虑实际测量时仍会代入一定的测量误差，设置注入误差：伪距测量误差均方差1 m，高度测量误差均方差3 m。仿真可得基于高度信息与时钟误差约束下的单星定位误差结果如图6 所示。

图6 基于高度信息与时钟误差约束下的单星定位

由图6 可知，基于高度信息与时钟误差约束下的单星系统在约100 s 便完成了1 km 精度的定位，所用时间远小于仅用CSAC 辅助的单星定位系统（约900 s），同时经100 次蒙特卡洛仿真统计可知系统可在200 s 完成327.25 m（RMS）的定位精度，在300 s 完成240.56 m（RMS）的定位精度，系统的整体性能均远优于仅利用CSAC 辅助的单星定位系统。仿真可得当伪距测量误差为1 m，连续观测200 s 时高度测量误差对系统定位精度（RMS）的影响如图7所示。

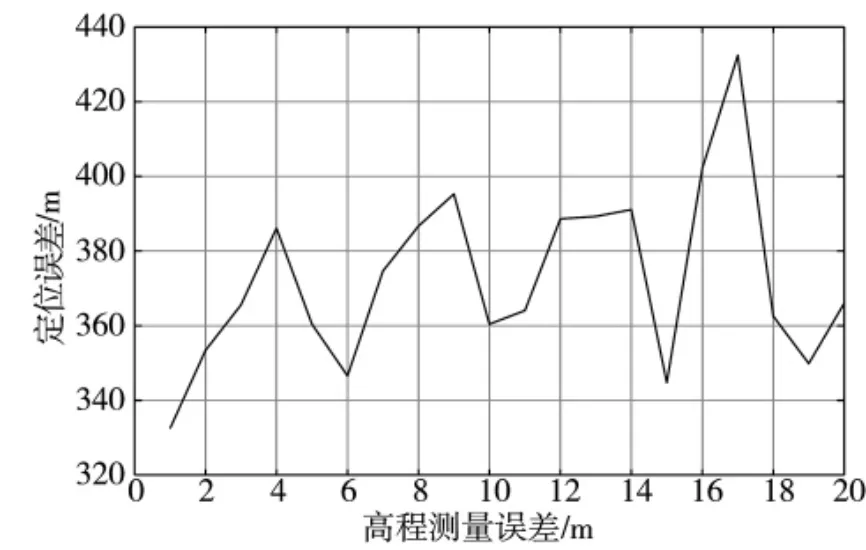
图7 高度测量误差对系统定位精度（RMS）的影响

由图7 可知与伪距测量误差相比，高程测量误差并不是造成高度信息约束下单星定位误差的主要误差源。由于该方法满足在紧急情况下仅利用单星测量数据定位的精度指标（定位时间<5 min，定位精度500 m），因此，可广泛应用于应急定位服务中。

2.2 静态试验验证

由于基于多源传感器信息的单星连续测距定位算法需求接收机对卫星连续观测一段时间方能定位，因此，该方法并不适用于载体动态环境下的实时定位，在利用实际数据对该算法做试验验证时也只能采用静态试验数据。本节利用GNSS 单频接收机、高精度气压高度计和CSAC，搭建基于多源传感器信息的单星定位静态试验环境，在卫星信号拒止环境下完成对一颗卫星信号的持续观测，并利用所获得的试验数据对单星定位系统进行了精度评估，最终验证基于多源传感器信息的单星连续测距定位算法在实际应用时的有效性。

2.2.1 验证环境

为验证所设计的单星连续测距定位算法的实用性，在实验室搭建静态试验数据采集和算法仿真验证环境如图8 所示。实验环境主要由Microsemi公司生产的型号为SA.45s 的CSAC、1 台Novatel OEM 638 高精度GNSS 接收机、台式计算机、1 根GNSS 天线、RAS-2 型气压高度计以及若干导线组成。

在实现单星静态定位试验数据采集与处理前，先进行两个预试验，分别为接收机高度测定试验和CSAC 驯服试验。其中接收机高度测定试验为静态试验提供接收机高精度高度先验信息，CSAC 驯服试验完成CSAC 对接收机内时钟的替代，从而为主试验的顺利完成奠定了基础，由于篇幅原因，本文对这两个预实验不做赘述。

2.2.2 定位数据分析

图8 单星定位静态试验环境

设置观测时间为2019 年9 月29 日22：10 到2019 年9 月29 日22：20。GNSS 接收机天线在该时间内只能接收PRN 编号为“5”的卫星数据，SA.45 s负责提供这一时段的时钟基准，先验高度信息为410.5 m。将接收机在0.5 h 内对“5”号卫星持续观测并记录的卫星星历数据和原始观测信息输入到计算机中分析处理，得到10 min 内卫星的实时位置与伪距测量值，利用高度信息和时钟误差约束下的单星定位算法，对这组数据进行定位解算并与接收机实际位置比较可得算法的定位精度，所得结果如图9 所示。

试验结果可知，真实接收机经过对一颗卫星的连续观测，辅以高精度CSAC 和气压高度计提供时钟和高度信息，可在2 min 内完成500 m 精度定位以及在5 min 内完成200 m 精度定位，完全符合战时应急定位精度需求。但由于CSAC 只能消除接收机时钟误差和钟漂，无法消除多路径效应、电磁干扰和接收机噪声等其他误差对伪距测量误差的影响，接收机内部模型也无法做到完整补偿，因此，仍有小部分噪声的存在引起定位结果收敛后的瞬时跳动。

图9 单星静态三维定位精度

3 结论

本文在假设接收机只获得一颗卫星信号的极端条件下，对基于多源传感器信息的单星连续测距定位算法及其精度分析作了理论分析探讨，在此基础上利用Matlab 软件对上述算法进行了仿真验证，最后搭建静态试验平台完成了C 多源传感器信息辅助单星定位算法的静态数据验证。仿真与实验结果表明，真实接收机经过对一颗卫星的连续观测，辅以高精度CSAC 和气压高度计提供时钟和高度信息，可在2 min 内完成百米级精度定位，完全符合战时应急定位精度需求。