舰艇编队多补给舰海上补给路径规划*
2021-03-24魏振堃赵素丽李阳超
魏振堃,赵素丽,李阳超,郭 湛
(陆军勤务学院,重庆 401331)
0 引言
随着国际局势的变化,我国受到来自海上的安全挑战日益增多,海上军事斗争准备日益艰巨,突破岛链束缚,走向远洋,为我国海外利益提供战略支撑成为当前我海军的重要使命任务。伴随保障是拓展舰艇编队行动半径的有效途径,是海军走向深蓝的重要举措。因此,研究舰艇编队海上补给路径规划问题,提高伴随保障效率,对于提高舰艇编队远洋伴随保障能力具有一定意义。
目前,国内外对舰艇编队海上补给路径规划问题进行了大量有益探索,主要将其视为旅行商问题(Traveling Salesman Problem,TSP)或者车辆路径问题(Vehicle Routing Problem,VRP)[1-7]。在TSP 模型或VRP 模型中,舰艇编队补给方式主要有3 种[8],即送报男孩(Delivery Boy,DB)方式、加油站(Gas Station,GS)方式,巡回牧师(Circuit Rider,CR)方式。DB 方式为补给舰到各个作战舰艇海域实施补给的方式;GS 方式为各个作战舰艇轮流到补给舰海域实施补给的方式;CR 方式为补给舰与作战舰艇共同到达某个海域实施补给的方式,3 种补给方式的示意图如图1 所示。
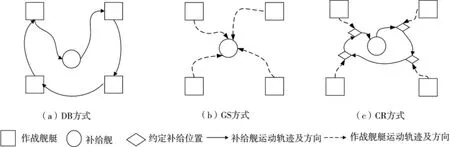
图1 舰艇编队补给策略
其中,GS 方式将所有作战舰艇集中于一处补给,目标相对集中,易受敌攻击;CR 方式同时调整补给舰和作战舰艇位置,舰船航行距离增加,模型复杂度增加,提高了运算成本。根据文献[6],采用DB 方式能最大限度地保证编队的基本作战阵型,随时可以进入战斗状态,同时在求解补给时间和规划方案的结果上更具有优势,因此,本文只考虑DB方式。
3 种方式均将单补给舰补给总时间最短作为唯一目标函数,对于大型舰艇编队往往存在多补给舰的情况,此时目标函数需要调整为在少用补给时间的情况下少用补给舰,此时模型变为双目标函数模型,即补给时间最短和参与补给任务的补给舰最少。国内对舰艇编队海上补给线路规划双目标函数模型比较少,其求解方式为设置函数权重后求和,从而转化成单一目标函数求解[2],这种求解方式主观性太强,结果往往不准确。从本质上讲,舰艇编队海上补给线路规划双目标函数模型是复杂多旅行商问题的衍生模型,难以求得精确解,采用启发式算法仍是求解该模型的最优策略。基于此,本文提出了一种基于改进GA 算法的舰艇编队多补给舰海上补给路径规划模型。
1 舰艇编队多补给舰海上补给路径规划模型
假设k 艘补给舰和n 艘作战舰艇组成的舰艇编队执行海上任务时,补给舰位于编队内部,在得到补给命令时,作战舰艇位置不动,补给舰按照一定顺序前往作战舰艇实施补给任务。
1.1 模型假设条件
抽象出的数学模型与舰艇编队海上补给实际情况略有不同,需要对相关细节进行合理假设,以方便建模求解。
1)舰艇编队中,k 艘补给舰对n 艘作战舰艇实施伴随补给;
2)补给舰从初始位置出发,按照一定顺序对所有作战舰艇实施补给后再回到初始位置;
3)每艘作战舰艇只补给一次;
4)补给舰船抵达作战舰艇补给海域,即刻就能补给,忽略补给准备时间,补给结束后即刻就能出发前往下一作战舰艇补给海域,忽略补给装备撤收时间;5)补给舰匀速航行;6)作战舰位置不动。
1.2 符号定义
N={1,2,…,n}:所有待补给作战舰艇的集合
K={1,2,…,k}:所有补给舰的集合
dij:补给舰从作战舰艇i 到作战舰艇j 所用的时间
ti:作战舰艇i 需要补给的时间
决策变量:

1.3 数学模型
综合考虑舰艇编队海上补给路径规划问题,在参与补给行动的补给舰数量尽量少的前提下,追求补给总时间最少。因此,舰艇编队海上补给路径规划模型为双目标函数模型[9],具体如下:
目标函数:

式(1)和式(2)分别表示补给舰数量最少和补给时间最短目标函数;式(3)和式(4)约束了一艘作战舰只能由一艘补给舰沿一条补给路线进行补给;式(5)约束了补给舰在补给完作战舰i 后,又从作战舰i 所在海域出发,保证线路的连续性;式(6)和式(7)约束了补给舰从初始位置出发并返回初始位置;式(8)参与补给行动的补给舰数量应不多于补给舰总数。
2 求解舰艇编队多补给舰海上补给路径规划模型的改进GA 算法
GA 算法是一种模拟生物界中遗传与进化的算法,通过染色体编码构建解空间、选择运算淘汰劣质父代、交叉运算产生优质子代、变异运算跳出局部最优,从而实现函数全局寻优。传统GA 算法只能进行单目标函数的最值寻优,不符合舰艇编队多补给舰海上补给路径规划模型的要求。本文在研究了舰艇编队多补给舰海上补给路径规划问题求解的具体特征后,在传统GA 算法的基础上增加了多目标函数寻优策略、采用了近时初始化方式构建初始解、改进了交叉和变异运算的运算规则,对问题的解空间进行充分搜索,并利用高效的选择机制,使种群不停向最优解空间聚集,达到快速寻优的目的,算法流程见图2[10]。
2.1 种群初始化
本文采用近时矩阵初始化方法构建初始解,近时矩阵定义如下。
近时矩阵,neartime(i,p)=j 表示舰艇j 是从舰艇i 出发用时第p 短的舰艇,记舰艇i 到自身的时间最长,即neartime(i,n+1)=i。若neartime(1,1)=3,则表明补给舰1 到作战舰艇3 的用时最短。
对于规模为M 的种群,初始化的具体步骤如下:
步骤1:对个体i(i≤M),置染色体X={1},迭代次数t=1;
步骤2:根据近时矩阵,在未被访问的舰艇集中选择到上一个访问舰艇用时最短的舰艇a 作为下一个补给舰艇,并更新X=X∪{a}和t=t+1;
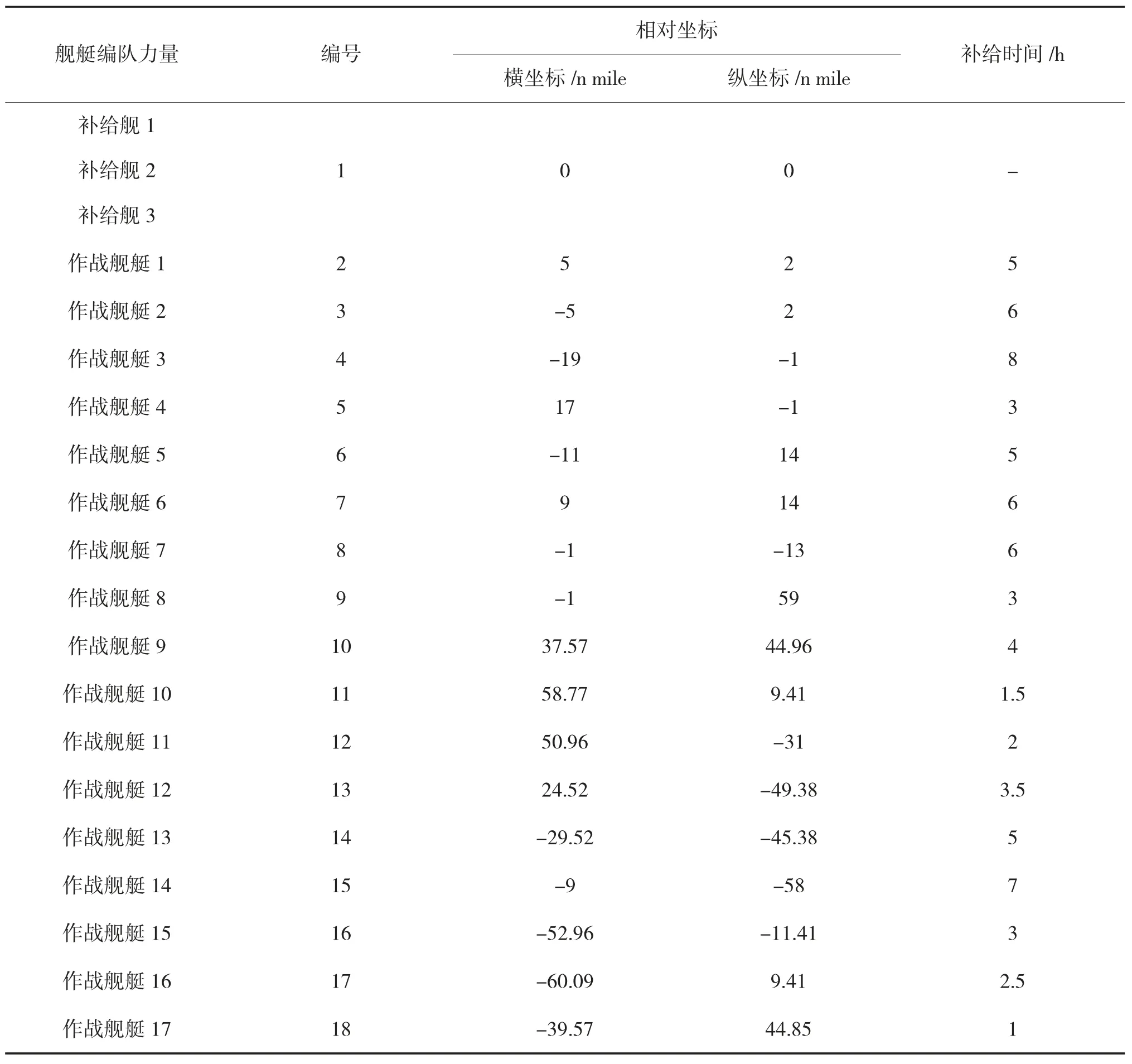
步骤3:若t 步骤4:随机产生k-1 初始断点; 步骤5:若i 图2 改进的GA 算法流程图 图3 染色体编码 本文采用单染色体编码,染色体上的每一个基因表示一个作战舰艇所在位置,用补给舰和作战舰艇所在位置的编号对每个基因进行编码。以8 艘待补给作战舰为例,图3 中2~9 分别为各作战舰艇的位置,1 为补给舰所在位置。当有2 艘补给舰时,会自动生成一个断点位置,若断点位置为3,则第1艘补给舰的补给路径为1→4→2→1,第2 艘补给舰的补给路径为1→5→7→9→6→3→8→1;当有3艘补给舰时,会自动生成两个断点位置,若断点位置为3、7,则第1 艘补给舰的补给路径为1→4→2→1,第2 艘补给舰的补给路径为1→5→7→9→6→1,第3 艘补给舰的补给路径为1→3→8→1。 在遗传算法中,通过适应度大小来区分种群中个体的优劣,故设计合理的适应度函数尤为重要。在求解舰艇编队多补给舰海上补给路径规划模型的改进GA 算法中,适应度函数为补给总时间,优化的目标就是选择能够使适应度函数尽可能小的染色体。 在进行选择运算时,采用保留精英策略,将父代种群中适应度函数最小的染色体复制到下一代种群中,剩余染色体按照轮盘赌的方式选择,这样能够保证遗传算法的收敛,使其向最优化方向进化。 交叉运算采用部分匹配交叉运算,选择进行交叉的父代,根据交叉概率确定是否进行染色体配对,交叉后的染色体作为子代染色体。随机选取两个父代染色体上的两个交叉位置,从而确定一段匹配基因,根据两个交叉位置之间的中间段给出的匹配关系生成两个子代染色体。例如: 对于下面两个父代染色体,随机地选择两个交叉位置“|”。 两个交叉位置之间的基因进行交换,得到 其中,x 代表暂未定义舰艇基因,得到匹配基因段的关系为: 9↔3,8↔4↔6,7↔5 然后将未选定的作战舰艇基因2 保留,于是得到 对于S1 中第7 个舰艇基因x,可以由7↔5,可得为5;对于S1 中第8 个舰艇基因x,可以由8↔4↔6 可得为4 或6,当x=4 时出现重复,于是x=6;对于S1 中第9 个舰艇基因x,可以由9↔3,可得为3;S2 同理,结果如下: 为提高全局搜索的能力,避免过早陷入局部最优解,本文设置了两种变异算子。 一种是普通变异算子,染色体内除1 号基因外任意两个基因片段相互交换,实现基因序列倒位,从而实现作战舰艇补给顺序的调整,例如染色体“123456789”,假设随机交换第2 位和第7 位,则有 另一种是反转变异算子,染色体上任意选择两个基因位置,两基因位置中间的所有基因进行逆序排列,例如染色体“123456789”反转位置为2 和5,则有 随机动态调整断点位置,从而实现对每艘补给舰补给作战舰艇数量的调整。 补给舰数量从k 开始循环,依次减少1,当补给舰数量由m(m∈K)减少到m-1,而最小补给总时间没有变化时,补给舰数量确定为m-1;补给舰数量为m-1 时的最优染色体即为最优补给方案。 运用电脑模拟生成了一组舰队编成,包括3 艘补给舰和17 艘作战舰艇,并以此为例进行舰艇编队多补给舰海上补给路径规划,对所提出的模型与方法进行验证。 3.1.1 原始数据输入 下页表1 为模拟生成的各补给舰和作战舰艇的相对位置,为方便计算,将3 艘补给舰均置于坐标原点,编队中3 艘补给舰位置为1,作战舰艇按照2~18 依次编号。 表1 舰艇编队基本情况统计表 3.1.2 参数设置 1)补给舰平均航速20 节(n mile/h); 2)改进GA 算法的相关参数设置:种群大小M=80,最大迭代次数T=5 000,交叉概率Pc=0.85,变异概率Pm=0.15。 运用改进GA 算法对舰艇编队多补给舰海上补给路径进行40 次MATLAB 实例仿真,选取仿真结果中的一个较好结果,其最优补给路径规划方案如表2。 各舰艇的相对位置和3 艘补给舰的海上补给路径结果见52 页图4 所示。 运用传统GA 算法对舰艇编队多补给舰海上补给路径进行40 次MATLAB 实例仿真,选取仿真结果中的一个较好结果,其最优补给路径规划方案如52 页表3。 表2 舰艇编队多补给舰海上补给路径规划方案 由表2 和表3,两种方案均需要调用3 艘补给舰,但是利用改进GA 算法规划的补给路径方案在补给时间上具有明显优势。 本文研究了舰艇编队多补给舰海上补给路径规划问题,通过模型分析和实例验证,所提模型能够较好地为舰艇编队中补给舰实施补给任务规划路线,实现最短补给时间和最少补给舰参与补给的双重目标。本文研究结论可为舰艇编队海上补给行为提供决策基础依据,具有较强的实用性和针对性。 图4 舰艇编队多补给舰海上补给路径规划图 表3 舰艇编队多补给舰海上补给路径规划方案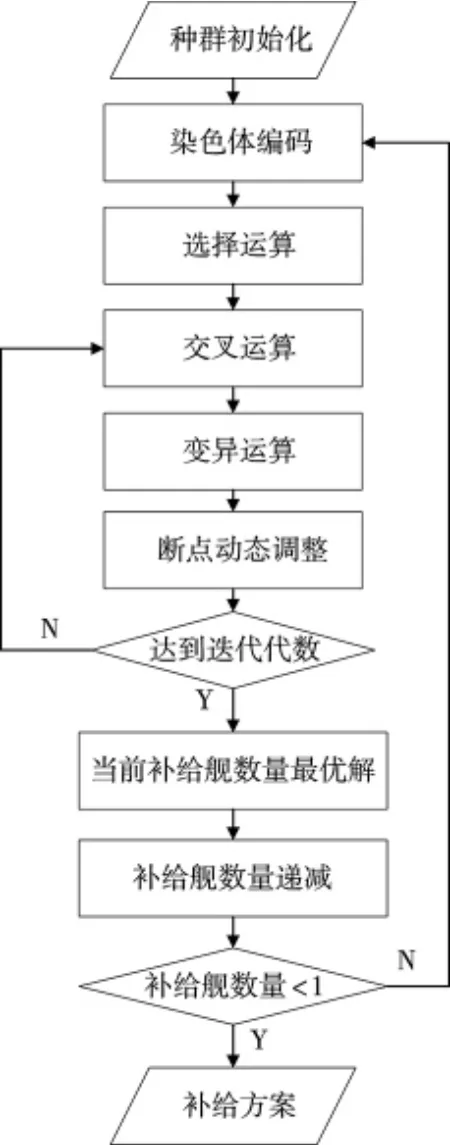

2.2 染色体编码
2.3 适应度函数
2.4 选择运算
2.5 交叉运算




2.6 变异运算


2.7 动态断点调整
2.8 补给舰数量控制规则
3 实例分析
3.1 原始数据输入和相关参数设置
3.2 舰艇编队多补给舰海上补给路径规划结果
3.3 舰艇编队多补给舰海上补给路径规划结果对比

4 结论