有源电力滤波器改进快速重复控制方法的研究*

王素娥，王鹏萱，郝鹏飞

(陕西科技大学电气与控制工程学院，陕西 西安710021)

随着非线性电子元件在生产活动中的广泛使用，使得电网要面对电子元件产生的谐波电流污染。有源电力滤波器(active power filter，APF)是目前抑制谐波有效的手段之一，由于其可以动态滤除各次谐波，且体积小、重量轻而受到广泛的研究与应用。APF 的谐波补偿控制器决定了其抑制谐波的能力[1-6]。 目前补偿电流控制方法中，比例积分(proportional integral，PI)控制可以对直流分量进行无静差控制，但是对谐波的抑制效果较差且对补偿电流跟踪精度较低[7]。 文献[8]将比例谐振控制器作为APF 的控制，可以有效地提高补偿电流跟踪精度，但是每个频率的交流信号都需要一个单独的比例谐振控制器进行控制，在实际应用中较为复杂。重复控制方法是基于内模原理而形成的，可以将其视为多个谐振的并联。 由于其对谐波的抑制能力较好，被广泛应用在APF 中[9-10]。 但是单独使用重复控制时系统瞬态性能较差，在负载突变时，无法快速响应而使得控制系统的动态响应速度受到影响[11]。文献[12]提出PI+重复控制的复合控制策略，但是该控制方法的动态性能受PI 的影响，使得系统的动态性能受到约束。

本文针对快速重复控制动态响应速度慢和稳定性差的问题，以三相并联型APF 为控制对象，采用一种比例控制与快速重复控制相结合的复合控制方法，通过前馈解耦在dq 同步旋转坐标系下实现，用于补偿2k±1 次谐波，从而可以消除所有的奇次谐波。 比例控制与快速重复控制相结合可以提高系统的稳定性，快速重复控制可以缩短固有延迟的周期。比例控制可以提高对基波信号的控制性能。

1 APF 数学模型与系统结构

1.1 APF 在旋转坐标系下的数学模型

三相并联型APF 系统结构图如图1 所示，usa、usb、usc分别为三相电网电压；L 为APF 侧滤波电感；R 为线路的等效电阻；C 为APF 的直流侧电容。 由图1 可得，APF 在三相a，b，c 静止坐标系下的数学模型为:

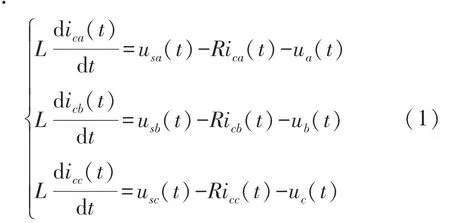
式中:ua，ub，uc为APF 的输出电压。

APF 输出的补偿电流一般由基波分量与谐波分量构成，为了方便控制谐波分量的补偿，将a，b，c静止坐标系下的式(1)经过等幅度变换矩阵M 转换为d，q 旋转坐标系下的式(3)，此为APF 在旋转坐标系下的数学模型。

图1 三相并联型APF 系统结构图

将式(3)做拉普拉斯变换可以得到APF 输出电压到输出电流的传递函数为式(5)，由此即可建立APF 在同步旋转坐标系下的数学模型。

式(7)为APF 输出的补偿电流表达式，可以看出，APF 输出补偿电流中的2k+1 次奇次谐波在旋转坐标系下转化为2k 次偶次谐波。 经过该变换后可以有效地降低重复控制的延时时间。

1.2 APF 的控制系统结构

为了改善控制系统的动态响应速度，控制系统采用双闭环控制。 电压外环使用传统比例控制，将电压环的输出信号与检测到的负载电流iL，abc所得到的指令补偿电流相叠加作为电流环的给定值，将APF 输出的电流ic，abc作为闭环控制，从而抑制非线性负载所产生的谐波。 本文的研究工作主要是电流环的控制策略。

2 改进的快速重复控制策略

2.1 传统重复控制性能分析

重复控制内模结构框图如图2 所示，可得，传统重复控制内模部分的传递函数为:

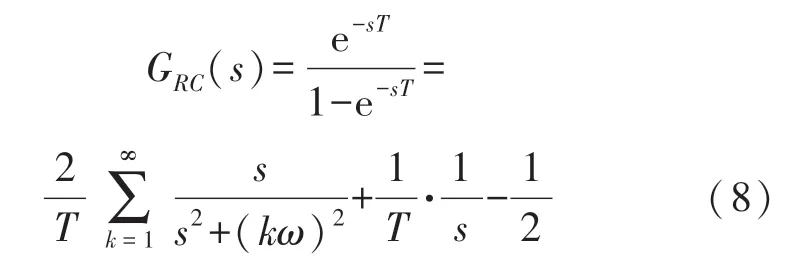
式中:ω 是基波频率；T 为参考信号的基波周期。

图2 重复控制内模结构框图

传统重复控制的伯德(Bode)图如图3 所示，从伯德图可知传统重复控制对各次谐波都具有高增益，并且可以对信号进行无静差跟踪。 但是重复控制应用在APF 控制时，由于延迟环节的存在使重复控制在动态响应过程中有一个基波周期的延迟，当非线性负载出现突变时，动态响应性能较差并产生大幅度的波动，从而影响系统的补偿效果。 为了提高控制系统的动态响应速度，本文使用比例控制与快速重复控制相并联的复合控制作为APF 电流内环的控制策略。

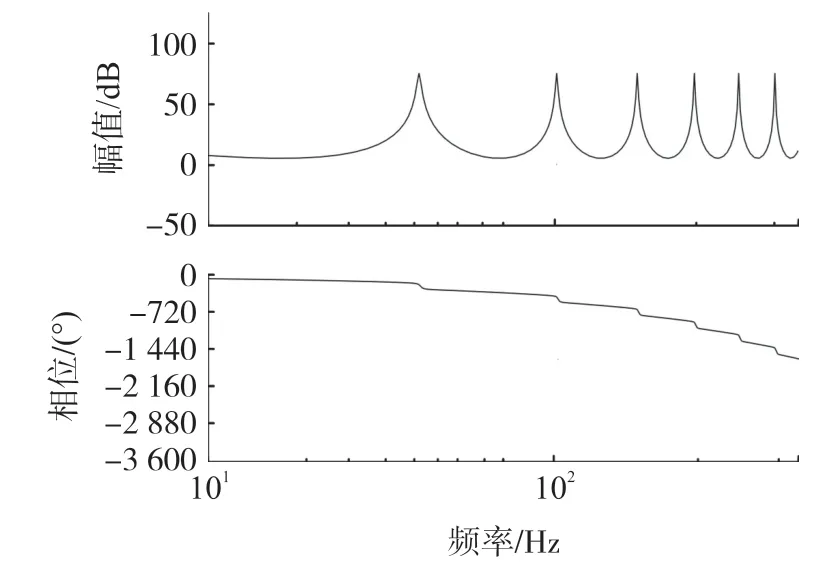
图3 重复控制的Bode 图

2.2 快速重复控制器设计

针对负载电流的奇次谐波经过旋转坐标变换后为偶次谐波的特性，本文提出一种快速重复控制策略，该控制策略可以消除所有奇次谐波。 从延迟环节可以看出，滞后的阶次降低使数据所占内存变小，进而可以实现运算量的减少。 快速重复控制的内模结构如图4 所示，可以得到其传递函数为:

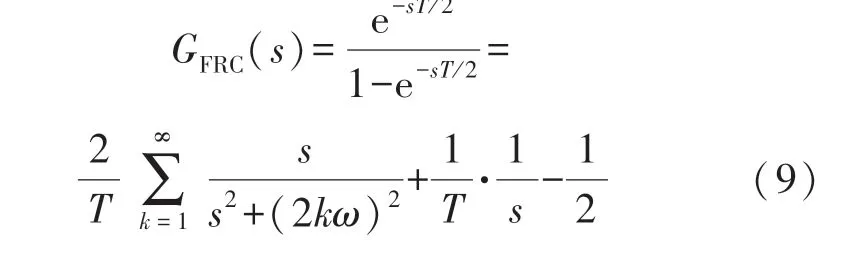
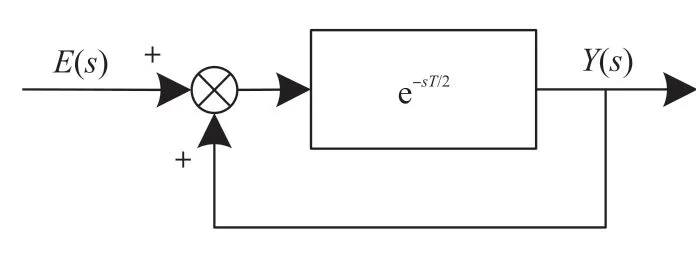
图4 快速重复控制内模结构框图

快速重复控制的伯德图如图5 所示，该控制方法在(2k±1)×50 Hz，k ＝1，2…处具有无穷大增益，可以有效地抑制电网中的奇次谐波。 此外，它还具有零相移的特性，即可以零稳态误差补偿2k 次谐波，保证了快速重复控制的稳定性。

图5 快速重复控制的Bode 图

2.3 快速重复控制稳定性分析

快速重复控制框图如图6 所示，其中，iref(z)为输入信号，ic(z)为输出信号，id(z)为电网中的干扰信号，e(z)为系统输入误差，G(z)为被控对象的传递函数，C(z)为补偿环节，Q(z)为滤波环节，z-N/6为延迟环节，N 为周期采样点数，虚线包含的部分为重复控制器。 进而可以得到系统电流闭环的传递函数为:

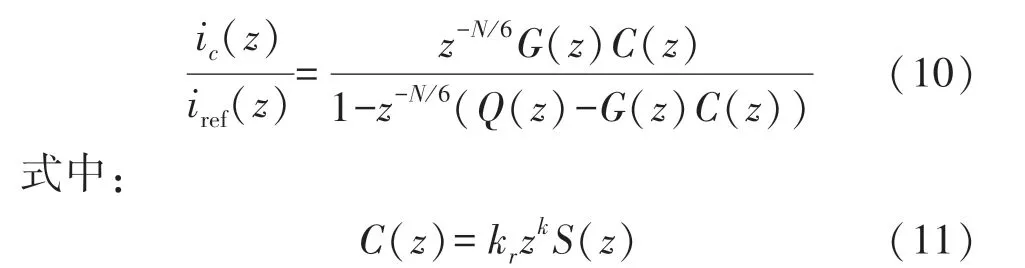
式中:kr为重复控制增益；S(z)为滤波环节；zk为超前环节。

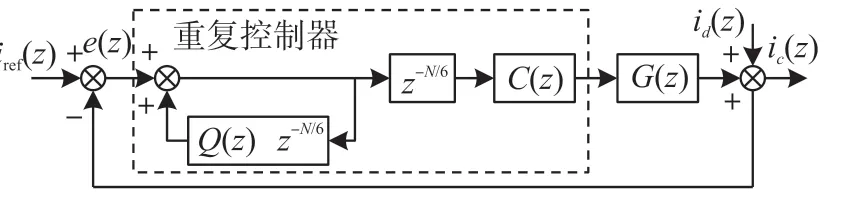
图6 快速重复控制框图

当控制系统稳定时，误差传递函数为

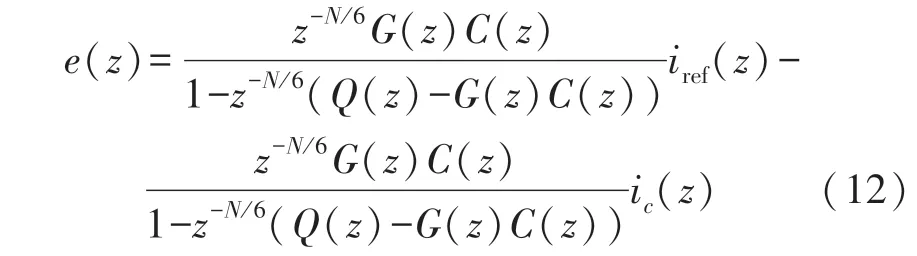
由式(10)与(12)可得，系统稳定的充分必要条件是

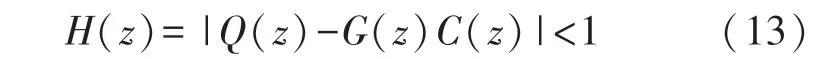
即H(z)的Nyquist 曲线在单位圆内部，就证明系统是稳定的。

根据传统快速重复策略对其控制参数取值，得到系统采用快速重复控制时H(z)的Nyquist 分布图，如图7 所示。 由图可以看出，式H(z)的Nyquist曲线的一部分在临近单位圆的地方，表明系统处于临界稳定状态，其稳定性相对较差。 由此可以看出单一的快速重复控制器在输入信号Iref(z)产生突变时，延迟环节的存在使得控制器延迟一个周期输出，导致动态响应速度较差的同时系统的稳定性也变差。

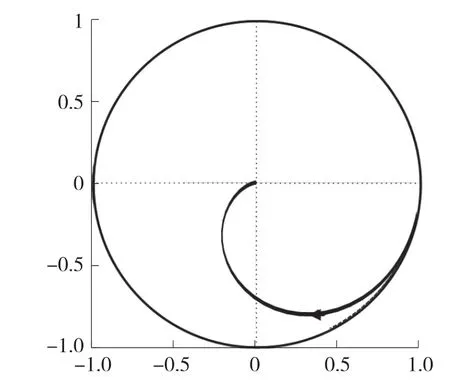
图7 H(z)的Nyquist 曲线

2.4 基于快速重复控制的复合控制策略

针对快速重复控制动态响应性能较差的问题，本文采用一种将比例控制与快速重复控制相并联的复合控制策略，该复合控制框图如图8 所示。 G1(z)为比例控制器，用作跟踪基波信号并提高控制系统的稳定性；G2(z)为快速重复控制器，用作补偿所有的(2k±1)次谐波分量并改善系统的跟踪精度，具体形式如式(14)所示。 复合控制策略可以有效地保证控制系统的稳定性和动态响应性能。

图8 复合控制框图

由式(17)可知，采用比例控制与快速重复控制并联的复合控制策略时，若使系统稳定要同时满足:

(1)单独采用比例控制时，H0(z)＝1+G1(z)G(z)的根全部在单位圆内。

(2)采用复合控制时，要使系统稳定应满足式(18)，其稳定条件矢量图如图9 所示。

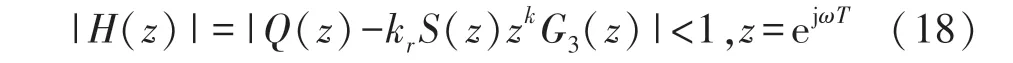
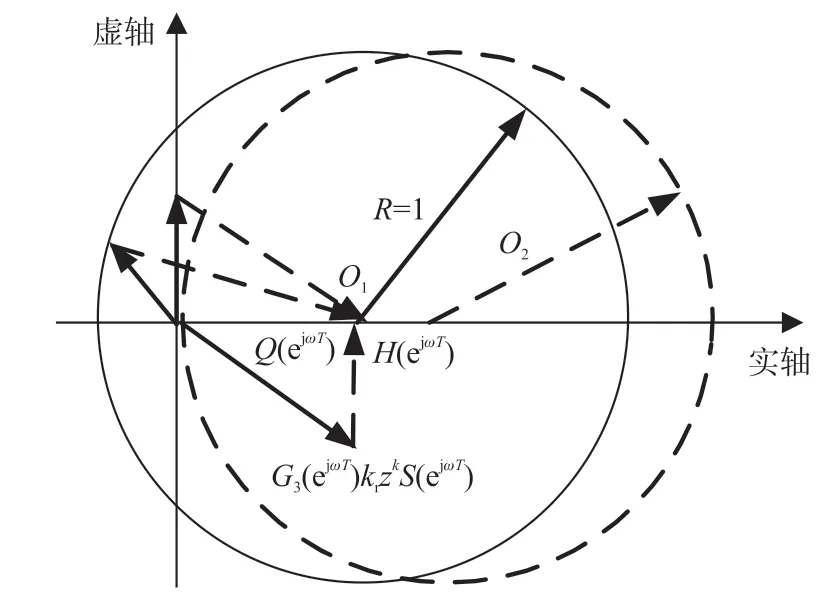
图9 复合控制稳定条件矢量图

2.5 补偿器的设计

kr为重复控制增益，其取值与系统稳定裕度成负相关，与系统的误差收敛速度呈正相关，在实际应用中kr取值通常小于1。

滤波环节S(z)主要对控制系统的幅值和相位进行补偿，从而使系统可以在低频段保证控制对象G(z)中低频段的幅值特性和零相移，还可以有效地加快系统高频衰减速度，从而改善控制系统的稳定性。由APF 的系统结构可知电流环被控对象的数学模型为1/(Ls+R)。 内模校正环节需要对传递函数G3(z)进行校正，可以得到其连续域的传递函数为:

zk为超前环节，通常用于补偿被控对象G3(z)和S(z)的相位滞后问题，可以使系统在中频段与低频段接近零相移。

3 控制器参数选择与仿真验证

本文使用Simulink 仿真平台，通过建立APF 的仿真模型，验证本文所提控制策略的可行性。 对比传统重复控制策略与复合快速重复控制策略的动态性能与稳态性能。 APF 主电路仿真参数如表1 所示。

表1 APF 主电路参数

3.1 控制器参数选择

根据上文所提的控制方法结合APF 的主电路参数设计控制器参数。 由于比例控制对系统稳定性有着很大的影响，因此需要预先设计其控制参数。 比例控制kp的取值根据2.4 节所述的稳定性判据1。 绘制H0(z)随kp变化的参数根轨迹如图10 所示，由图可知当0＜kp＜50 时，H0(z)的根都分布在单位圆内，满足稳定性判据1。 在实际应用中，考虑到稳定裕度，取kp＝1。

超前环节zk的补偿效果如图11 所示，根据系统稳定条件2，为保证系统的稳定，需要保证向量H(z)的轨迹总是在单位圆内，所以Q(z)的取值小于1，本设计取Q(z)＝0.95 可以保证控制系统的稳定；重复控制增益kr取0.2。 本文的采样频率为20 kHz，考虑到在实际应用中APF 用来补偿40 次以内基波频率的谐波，故选取截止频率为2 kHz 的二阶低通滤波器作为补偿器S(z)，可以得到其在离散域下的传递函数为式(20)。

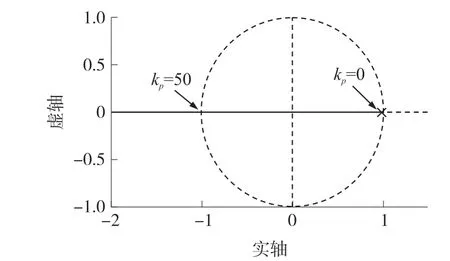
图10 H0(z)随kp 变化的根轨迹

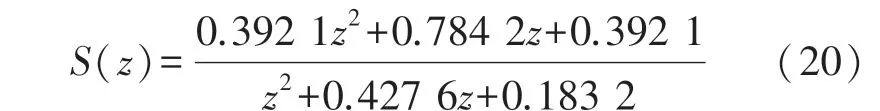
超前环节zk参数的选取由补偿被控对象G3(z)和滤波环节S(z)共同决定，其对S(z)G3(z)的补偿效果如图11 所示。 当取k ＝3 时，可以实现对系统相位滞后的有效校正。

系统采用复合控制时H(z)的Nyquist 曲线如图12 所示。 由图可知该复合控制的Nyquist 曲线在单位元内，根据式(18)的稳定性判据可以看出该复合系统稳定。

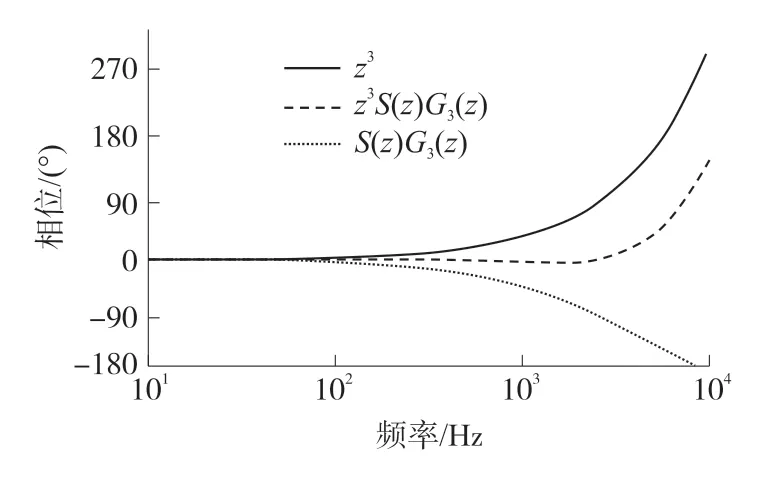
图11 超前环节zk 的补偿效果图

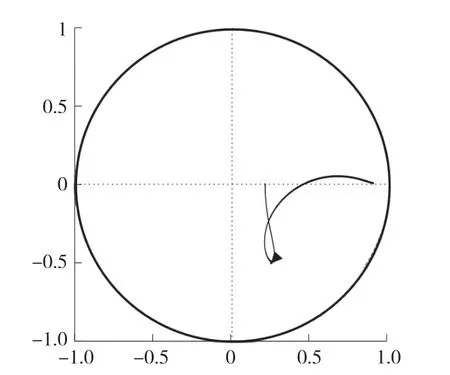
图12 H(z)的Nyquist 曲线

3.2 仿真验证

负载电流的THD 如图13 所示，由图可知负载电流iL中的奇次谐波含量较高，谐波的THD 为29.62%。

系统采用传统重复控制与复合控制时电网电流THD 分别如图14(a)和(b)所示，由图可知，采用复合控制时电网电流isa的THD 值相比于传统重复控制，由4.65%降为3.14%，可以精确地补偿40 次以内的所有奇次谐波，从而证明了该复合控制方法的有效性。 图15 为采用复合控制时系统处于稳态的电流仿真波形，其中isa、iLa和ica分别为电网电流、负载电流和APF 的输出电流。

图13 负载电流THD

图14 电网电流THD

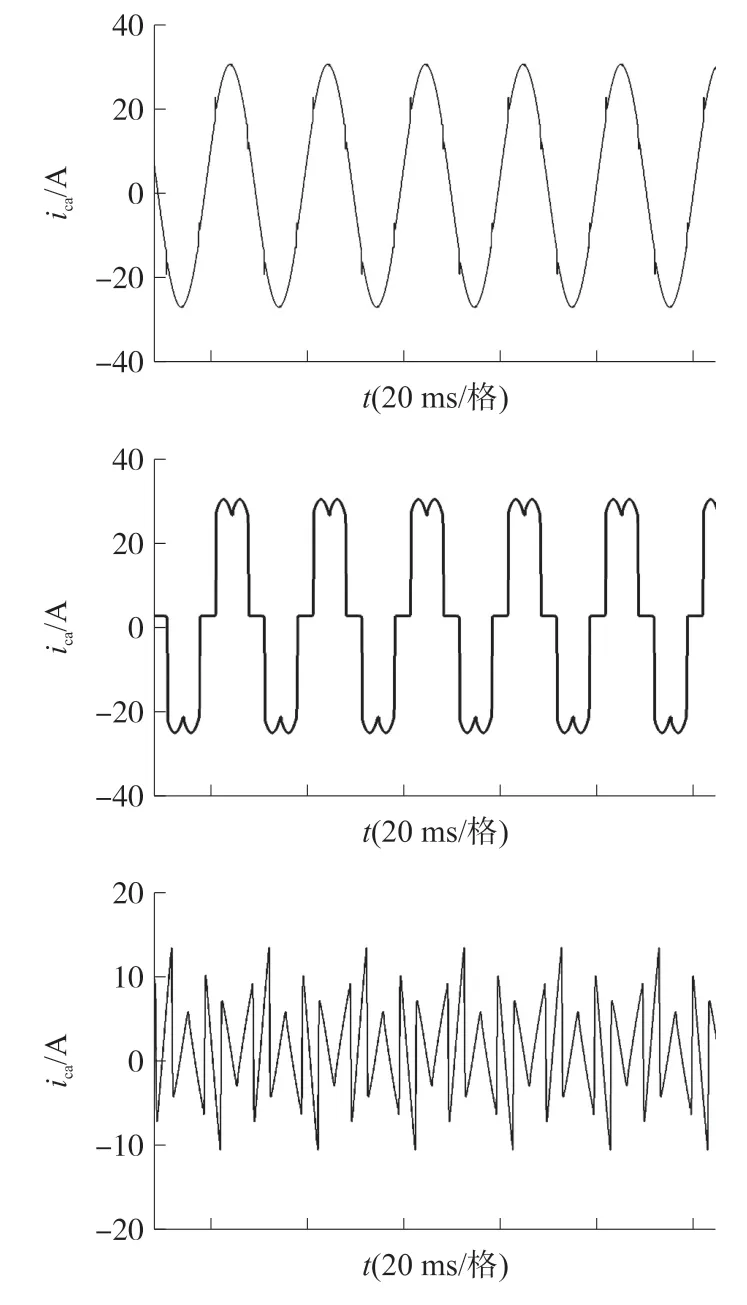
图15 复合控制电流稳态波形

为验证复合控制的动态响应速度，在0.3 s 时将负载在从半载状态变为满载状态，传统重复控制与复合控制的动态响应波形分别如图16 与图17 所示。

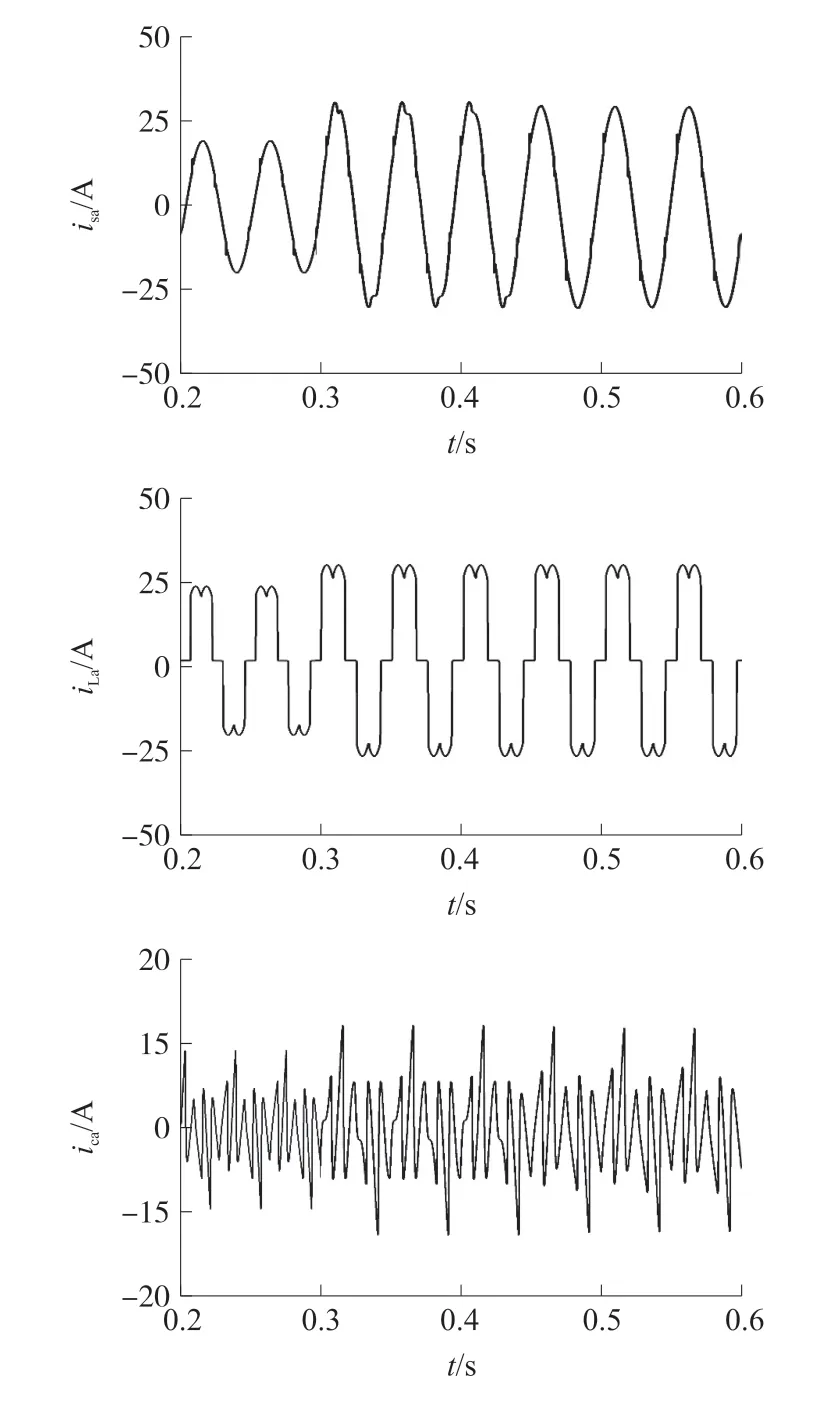
图16 传统重复控制动态响应波形

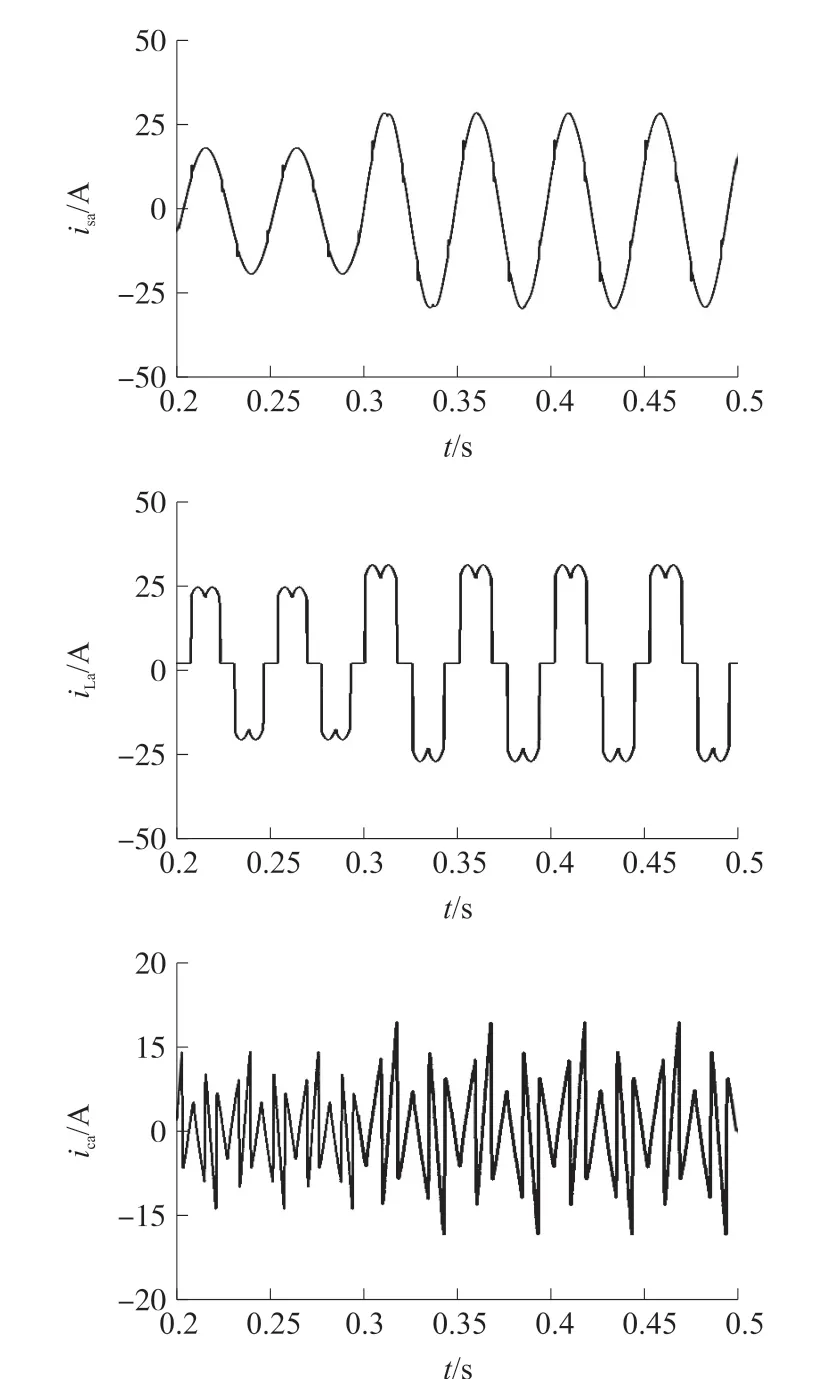
图17 复合控制动态响应波形

由图可知，当负载发生突变时，传统重复控制的电网电流波形需要3 个周期才可以恢复正常，而复合控制在1 个周期以内就可以恢复正常。 相比于传统重复控制，改进型复合控制瞬态响应时间更短。仿真结果表明，该复合控制策略的瞬态响应速度有了较为明显的提高，并且延迟时间也有所减少，其可以快速地对输入电流谐波的变化做出反应并且达到稳定状态。

4 结论

本文针对APF 电流内环采用传统重复控制策略时动态响应速度慢的问题，分析了电网中的电流谐波主要为奇次谐波，奇次谐波经坐标变换，在dq 同步旋转坐标系下为偶次交流分量。 提出了针对奇次谐波的改进快速重复控制策略，即将比例控制与快速重复控制相结合的复合控制策略，并在MATLAB/Simulink仿真平台进行仿真验证。 可以得出以下结论:(1)与传统重复控制策略相比该复合控制策略可以有效地提高系统对奇次谐波的补偿精度；(2)该复合控制策略只有对奇次谐波有抑制效果，可以将内模延时时间减少一半，从而提高了输入电流谐波的动态响应，有效地改善系统整体的响应速度；(3)该复合控制策略缩短了内模环节的延迟周期，数据存储量小，可以有效地节省数据储空间。