用于双有源桥DC-DC 变换器的全局效率最优调制方法

韩会山，毕艳军，梁 舒

(邢台职业技术学院电气工程系，河北 邢台054000)

随着社会进步，新能源的发展逐步成为各个国家的首要战略目标。 双有源全桥(Double Active Bridge，DAB)双向DC-DC 变换器以其控制方式灵活、动态响应快、结构对称等特点，以及易于串并联，适应高低压变化，具备能量双向传输等优点，得到了广泛的关注[1-2]。 同时，DAB 变换器在电动汽车与电网互动(V2G)、储能系统和电源供电系统等方面具有重要的应用前景[3-4]。

自从DAB 变换器被提出以来，相关研究主要集中在其调制策略、功率传输特性、软开关实现以及控制方法等方面。 在调制策略方面，通常包含有单移相调制(SPS)、双重移相调制(DPS)和三重移相调制(TPS)等。 SPS 调制方式是最常用的调制方法之一，其控制方法简单，但无法调节和控制变换器回流功率与电感电流有效值[5]。 一些学者认为DAB 变换器存在功率回流现象造成了传输效率的下降，从减少回流功率方面研究了DPS 等调制方式。 其中，文章[6]所提方法降低了DAB 变换器运行时的无功回流功率。但对于DPS 调制方式来说，电路系统的无功环流仍旧很高，这限制了变换器系统进一步提高传输效率。TPS 调制方式涵盖了SPS 与DPS 调制方式，理论上可以实现更优的控制效果[7]。 文章[8]提出一种TPS调制策略，提高了DAB 变换器的传输效率，计算出了最优控制量使DAB 变换器拥有最小化的电流应力和导通损耗。 该方法虽然减小了电感电流，但并没有直接以效率最优为控制目标，因此其传输效率未在最优状态。 此种方式下，建立精确而复杂的最优效率目标函数将导致全局最优调制参数难以被确定。

本文提出了一种基于粒子群优化(PSO)算法的DAB 变换器全局效率最优调制方法。 其根据变换器系统的电路参数与实时的工作状态建立了精确的最优效率目标函数。 设计三重移相占空比控制器，可以根据给定的传输功率，利用PSO 算法搜索系统最优调制参数，从而得到最优三重移相占空比，使得DAB 变换器在全负载范围内始终工作在传输效率最优的状态。

1 电路拓扑与数学模型

图1 为DAB 变换器的电路拓扑结构，其由开关管Q1～Q8构成的两个电压源型有源全桥、高频变压器T1、谐振电感Lr、以及两个直流母线支撑电容C1、C2组成。 在该拓扑中，Lm为高频变压器的励磁电感。在移相调制策略中，各个桥臂的上下开关管均为互补驱动信号。 一、二桥臂的桥口输出电压为vp；三、四桥臂的桥口输出电压为vs；一次侧直流母线电压值为V1；二次侧直流母线电压值为V2；电感Lr两端电压为vL；电流为iL。 定义变换器的开关周期为2T。

在TPS 调制方式下，DAB 变换器各个开关管的驱动信号波形和桥口电压波形vp、vs如图2 所示。

图1 DAB 变换器电路拓扑

图2 DAB 驱动波形与桥口电压波形

TPS 调制方式下，所有开关管都为50%占空比。其中开关管Q1、Q2的驱动信号分别超前开关管Q5、Q6为D0×180°；开关管Q1、Q2的驱动信号分别超前开关管Q4、Q3为D1×180°；开关管Q5、Q6的驱动信号分别超前开关管Q8、Q7为D2×180°。 其中，移相占空比D0取值范围为-1 ～1，D1取值范围为0 ～1，D2取值范围为0～1。 可以看出，TPS 调制方式拥有三个控制自由度，可以通过适当选取三个控制变量，使DAB 变换器工作在效率最优状态。

如式(1)定义方波函数S(t)，占空比为0.5、周期为2T。

根据图2 可知，桥口电压波形vp(t)、vs(t)为如式(2)、式(3)所示的三电平方波。

根据电路拓扑结构与vp(t)、vs(t)公式，可以简化DAB 变换器的数学模型如图3 所示。 其中，原副边全桥分别被简化为两个串联的电压源，高频变压器在理想情况下被省略，n 为变压器的变比。

图3 DAB 变换器等效模型

根据图3 及电感伏秒平衡公式，可以推导出变换器稳态工作时电感电流的有效值平方表达式与变换器的传输功率表达式，分别如式(4)、式(5)所示。

对于不同的D0、D1、D2，式(4)、式(5)的形式不同，因此传统方法无法对不同工作点进行统一的分析。 设置直流电压V1为500 V，V2为240 V，开关频率为20 kHz，变压器变比为1 ∶1，Lr为47 μH。 根据式(4)、式(5)与TPS 占空比的取值范围，可以建立三维传输功率分布图与电感电流有效值平方分布图，分别如图4、图5 所示。

图4 DAB 变换器传输功率分布图

图5 DAB 变换器电感电流均方值分布图

图4 与图5 中，三维坐标系中任意一点的坐标分别对应三重移相占空比D0、D1、D2。 该点的颜色深浅表示相应取值的大小。 对应于某一给定的传输功率，输入变量有多种不同的组合形式。 对于这些不同组合形式，得到的电感电流有效值不同。 在DAB 变换器中，由于电路存在阻抗，电感电流造成了变换器的功率损失。 通过相关算法对输入变量D1、D2、D3进行合理规划，将会得到一种最优组合，使变换器传输功率一定时，对应的功率损失最小，这样变换器就能工作在效率最优的状态下。

2 改进粒子群优化算法

PSO 算法属于AI 智能算法，具有实现较为简单、控制参数少且不依赖目标函数的特点。 目前，部分学者在电力电子技术相关的问题中尝试应用PSO理论，并取得了很多研究成果[9]。

三维空间中粒子群算法模型如式(6)、式(7)所示。

向量xi(j)表示粒子在三维向量空间中的位置，下标“i”表示第i 个粒子，“j”表示粒子的第j 代；vi(j)为粒子的速度向量，表示粒子运动快慢；向量pg(j)、pi(j)分别为粒子群群体的最优位置与个体的最优位置；ck为粒子的加速度常数；w 为惯性权重系数；rk(j)为三维均匀分布随机函数，其每个维度的取值范围为0～1；N 为粒子总数；J 为最大迭代次数。

PSO 算法通常更适用于求解非约束优化问题，在求解非线性约束问题时，需要如式(8)构造带有惩罚因子的广义目标函数改进粒子群算法。 其中，每一个粒子的适应度函数为F(xi(j))＝F(D0，D1，D2)，以最小值为目标。

式中:f(xi(j))为原目标函数，如式(9)所示；h 为惩罚力度(通常取500～1 000)；H(xi(j))为惩罚因子，如式(10)所示；Ω 为xi(j)的可行域，由D0、D1、D2的取值范围确定。

式(9)中目标函数f(xi(j))设计为系统总损耗，当系统损耗最低时，认为传输效率最高。 其中系统损耗包括了线路内阻损耗与开关损耗。 当使用IGBT 开关管时，还应包含IGBT 压降产生的导通损耗。

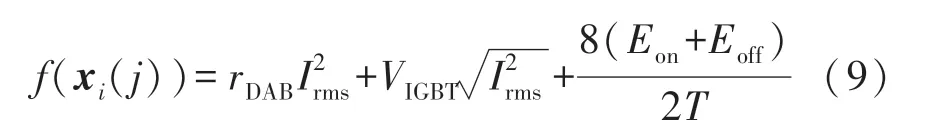
式中:rDAB为回路总内阻，VIGBT为回路中IGBT 的总压降，(Eon+Eoff)为单个开关管的开关损耗能量，通常可以从器件的数据手册中得出。

式(10)的惩罚函数保证了输出功率等于给定传输功率。

根据粒子群算法模型，DAB 变换器全局效率最优控制方法如下，共分为9 个阶段。

阶段1，初始化粒子群:初始时刻，根据经验设置加速度常数c1、c2(通常为0 ～2)、惯性权重w(通常为0.5～1)、粒子数量N(通常为200 ～500)、最大迭代次数J(通常为500 ～2 000)。 随机设置粒子群内各个粒子的起始位置xi(0)，并根据式(8)对每一个粒子的适应度进行求解。 依此设置粒子群群体最优位置pg(0)与个体最优位置pi(0)。 初始化粒子的初速度vi(0)(粒子每个维度的初始速度通常为0～0.2)。 执行阶段2。

阶段2，变量更新:更新电压值V1、V2；传输功率给定Pset；电感值Lr。 执行阶段3。

阶段3，粒子位置计算:根据式(7)计算并更新粒子群内每一个粒子的最新位置。 若计算位置超出可行域，则通过降低当前速度vi(j)，将粒子限制在系统所划定的可行域边界之内。 执行阶段4。

阶段4，加入微小扰动:若发现某粒子的速度为零，则如式(11)所示，加入微小扰动(z 通常小于0.05)。 此方法避免了粒子群内的粒子静止不动，有利于提高PSO 的动态性能。 执行阶段5。

vi(j+1)＝vi(j+1)+z·r(j) (11)

阶段5，粒子速度计算:根据式(6)计算并更新粒子群内每一个粒子的速度。 执行阶段6。

阶段6，粒子适应度计算:根据式(8)～式(10)，计算并记录粒子群各个粒子的适应度函数F(vi(j+1))，用于之后的位置更新。 执行阶段7。

阶段7，个体最优位置更新:根据阶段6 中的记录结果与历史个体最优位置的适应度函数比较。 若某粒子当前位置的适应度较优，则更改该粒子的个体最优位置pi(j+1)为当前所处位置。 执行阶段8；

阶段8，群体最优位置更新:根据阶段6 中的记录结果找到本轮迭代内的群体最优位置，并与群体最优位置比较适应度，将较优位置设置为群体最优位置pg(j+1)。 执行阶段9；

阶段9，终止条件判断:将群体最优位置的坐标作为TPS 占空比D0、D1、D2输出给开关管驱动单元。 判断当前迭代次数，若达到最大迭代次数，则此次粒子群优化结束，否则跳回阶段2 继续执行PSO算法。

利用上述方法可以处理复杂的全局效率最优目标函数，同时可以实时寻优三重移相占空比，使DAB 变换器在全负载范围内以最优传输效率运行。保持了较低的回流功率、电感电流峰值和有效值。

3 仿真与实验验证

为了验证本文所提方法的有效性与正确性，首先在MATLAB 环境下对其进行了仿真验证，其次搭建平台进行了实验验证。 设置直流电压V1为500 V，V2为240 V，开关频率为20 kHz，变压器变比为1 ∶1，Lr为47 μH。

图6 为DAB 变换器在不同给定功率时的MATLAB 闭环仿真波形。 仿真波形分别为Vp(t)、Vs(t)电压波形与电感电流波形，分别标记为VB1、VB2与IL。

图6 分别显示了不同传输功率时的工作波形，变换器正常工作。 进一步，随着给定功率增加，PSO优化后的TPS 占空比的变化轨迹如图7 所示。

图6 不同给定功率下的闭环仿真波形

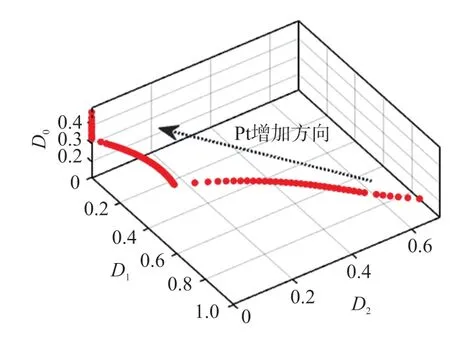
图7 PSO 优化后的TPS 占空比轨迹

可以看出，变换器的最优调制方式从TPS 调制方式，DPS 调制方式到SPS 调制方式逐渐变化。 在全工作范围内，本文所提方法均能对三重移相占空比进行寻优，并能实时得到最优控制量，使DAB 变换器在全负载范围内以最优传输效率运行。

如图8 所示为传输功率为8 kW 时的实际电路工作波形，图中分别表示了Vp电压波形、Vs电压波形与电感电流波形iL。 此时原边电压峰值为500 V，副边电压峰值为250 V，电感电流有效值约为36 A，实验结果与仿真结果一致，证明了本文所提调制策略下DAB 变换器可以正常稳定的工作。

图9 所示波形分别为同一DAB 变换器下的SPS方式效率曲线、DPS 方式效率曲线、TPS 方式效率曲线与经过本文PSO 算法优化后的TPS 效率曲线。

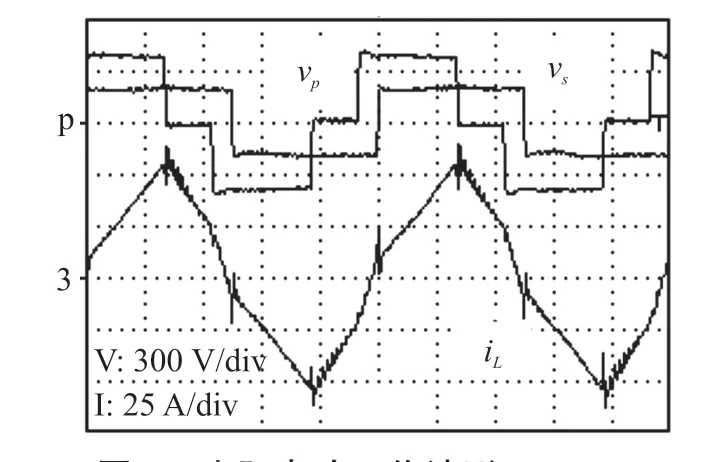
图8 实际电路工作波形(8 kW)

图9 DAB 变换器效率对比曲线

由图9 得出，全工作范围内，本文算法下的TPS方式传输效率优于传统的SPS、DPS 方式与经典TPS 方式。 相比于经典TPS 方式，本文所提方法显著提高了变换器在轻载时的效率。 实验结果验证了粒子群算法应用在实现DAB 变换器全局效率最优的三重移相占空比寻优方法上的正确性与可行性，也说明了所提方法的实际应用价值。

4 结论

针对TPS 调制方式下，难以建立精确而复杂的最优效率目标函数的问题，提出了一种基于粒子群优化(PSO)算法的DAB 变换器全局效率最优调制方法。 该方法根据变换器参数、工作状态和给定传输功率实时搜索系统最优调制参数，得到最优三重移相占空比，使得DAB 变换器在全负载范围内始终工作在传输效率最优的状态，且保持较低的回流功率、电感电流峰值和有效值。 本文通过MATLAB 仿真与实验验证了该算法的性能，证明了所提方法的正确性与实际的可行性。