基于特征向量空间重构的方向图保形算法
2021-03-23陈子昂杨嘉伟魏晓磊陶琛琛
陈子昂, 杨嘉伟, 魏晓磊, 陶琛琛
(1.北京遥感设备研究所,北京 100854; 2.中国航天科工防御技术研究院,北京 100854;3.火箭军装备部,北京 100085)
0 引言
自适应波束形成技术在阵列雷达信号处理领域有着广泛的应用。传统的自适应波束算法能够有效地抑制旁瓣干扰[1],然而实际的电磁环境中,干扰还有可能从波束主瓣进入,此时,自适应波束形成算法会导致主瓣波束形状发生畸变、旁瓣电平升高以及输出信干噪比(SINR)降低等问题,严重影响了雷达测角精度[2],因此如何更好地抑制主瓣干扰的问题备受学者们的关注。为此,文献[3]中提出了一种基于阻塞矩阵预处理方法,通过对主瓣干扰信号进行阻塞,然后进行自适应处理,从而实现抑制干扰同时主瓣方向图保形,但这种算法会降低阵列自由度,而且不能解决旁瓣升高的问题;文献[4]提出了特征投影矩阵预处理(Eigen-projection Matrix Processing,EMP)的方法,实现了不降低自由度的主瓣保形,但EMP算法会存在主波束偏移的问题;文献[5]中利用特征投影矩阵预处理和协方差矩阵重构的方法(Eigen-projection Matrix Processing and Covariance Matrix Reconstruction,EMP-CMR),降低了算法复杂度,通过削弱噪声随机性的影响,改善了EMP算法带来的主波束偏移的问题,提高算法稳健性,但其只适用于单主瓣干扰的情况;文献[6]提出了一种基于子空间滤波和协方差矩阵重构的方法(Subspace Matrix Filtering and Covariance Matrix Reconstruction,SMF-CMR),有效抑制了多个主瓣干扰。
虽然EMP算法和之后的改进算法能有效地抑制干扰并实现主瓣保形,但EMP算法中对主瓣干扰的屏蔽是建立在干扰特征向量与导向向量近似相等的条件下[7],当主瓣干扰信号强度并非远小于旁瓣干扰时,其特征向量对应的投影矩阵可能包含旁瓣干扰导向向量的分量,采用该投影矩阵做处理的自适应算法会降低对旁瓣干扰的抑制效果,使得输出信干噪比显著下降。为了解决这一问题,一种基于空间谱分解与协方差矩阵重构的新方法在文献[8]中被提出,但其被指出存在干扰方向能量谱泄露的问题[9],对此文献[9]提出了一种基于MUSIC算法的高精度波达方向(Direction of Arrival,DOA)估计的方式重构干扰子空间,而文献[10]提出了一种迭代自适应(Iterative Adaptive Approach,IAA)的方式重构干扰子空间,这两种算法拥有更高精度DOA和能量谱估计,但存在复杂度较高、DOA估计误差对结果影响较大的问题,特别是当干噪比较低时其估计误差不可避免,并且在多主瓣干扰的情况下干扰抑制效果降低。
为了解决同时存在一个强主瓣干扰和一个弱主瓣干扰的情况下干扰抑制和方向图保形的问题,本文提出了一种新的主瓣干扰特征向量空间重构的方法,通过特征向量与主瓣子空间的正交性分析以及主瓣干扰与旁瓣干扰的相对强度做比较,确认主瓣干扰对应的特征向量,由此来构建主瓣干扰特征向量空间,从而实现主瓣方向图保形与对干扰的抑制。仿真实验验证了方法的可行性。
1 信号模型与EMP算法
1.1 阵列信号模型
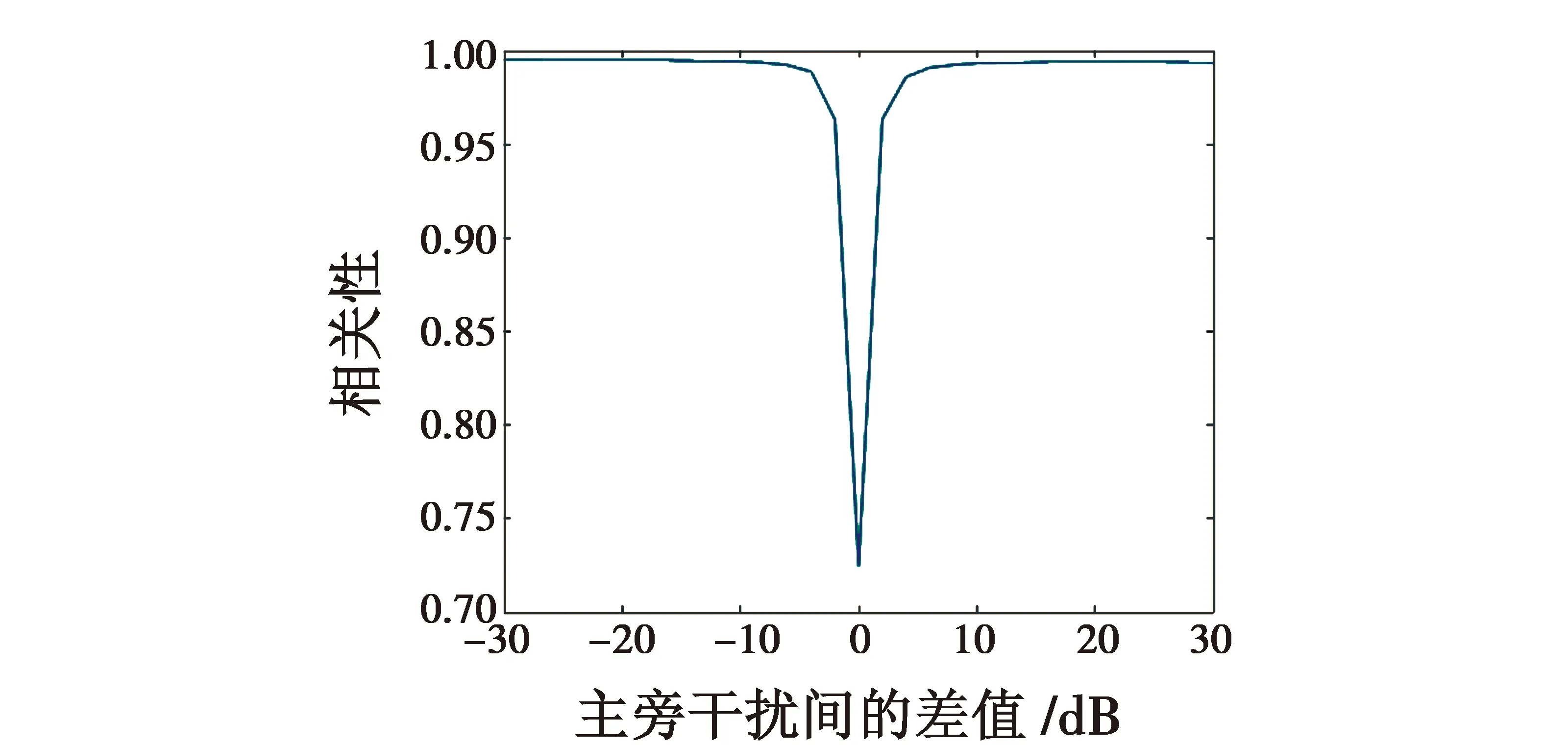
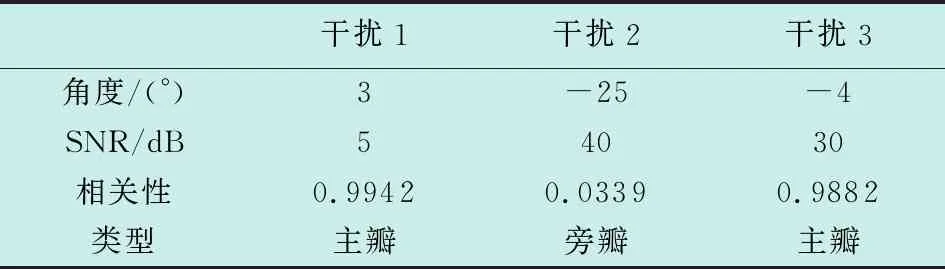
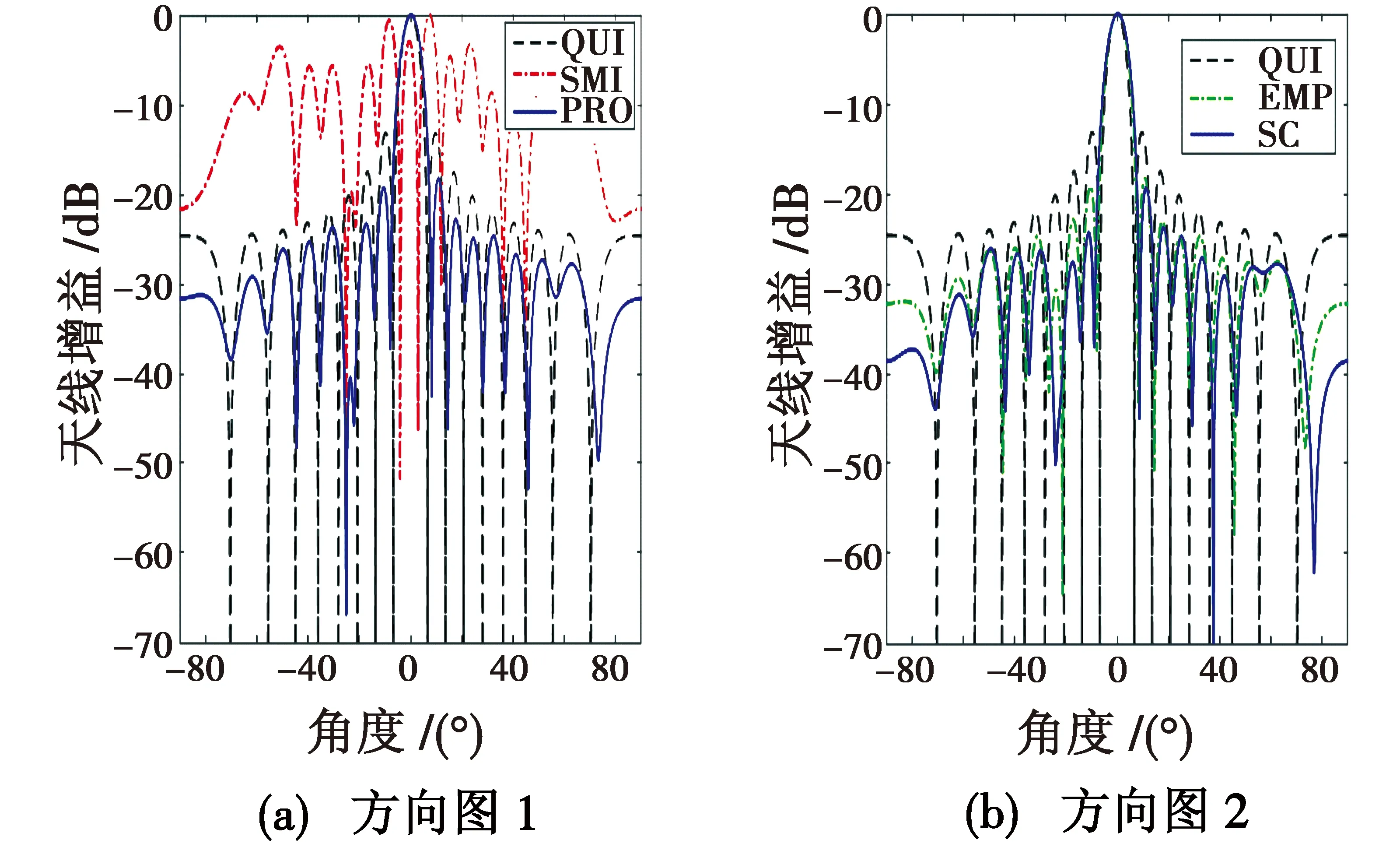
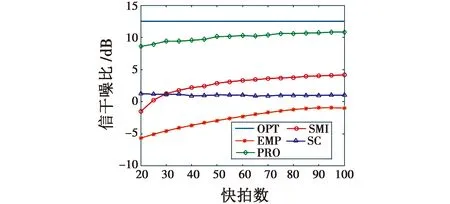
考虑由N个阵元组成的阵列,阵元间距为半波长,远场存在P个窄带干扰信号,其中有M个位于波束主瓣,且P (1) (2) (3) 式中:L代表采样快拍个数,对采样协方差矩阵进行特征分解得到 (4) 式中:λi和ui分别为特征值和对应的特征向量,并且将特征值按从大到小排序,即满足λ1≥λ2≥…≥λN;Λs=diag(λ1,λ2,…,λP)为P个大特征值组成的对角阵,对应P个干扰信号的特征值;Us=(u1u2…uP)为其特征向量共同构建的矩阵,张成干扰对应的子空间;Λn=diag(λP+1,λP+2,…,λN)为N-P个小特征值组成的对角阵,对应噪声信号的特征值;Un=(uP+1uP+2…uN)为其特征向量组成的矩阵,构成噪声子空间。 EMP算法从干扰子空间中判断主瓣干扰对应的特征向量并构成主瓣干扰子空间,并认为干扰的特征向量与干扰方向的导向向量一一对应且互相正交,假设Um为主瓣干扰对应的特征向量构成的子空间,则 Um=(u1u2…uM) (5) 确定主瓣干扰特征向量的方法为 (6) 式中:ρ为常系数因子;aq为静态导向向量。则主瓣干扰子空间的投影矩阵为 (7) 回波信号X通过正交投影矩阵B进行预处理,得到了去除主瓣干扰成分的采样数据 Y=BX (8) 再经过噪声白化处理后,得到的旁瓣干扰加噪声协方差矩阵为 (9) 最后根据最小方差无失真响应(MVDR)准则,得到自适应处理后的最优权值 (10) 此时阵列输出的信号可以表示为 (11) 采用子空间投影的方法实现干扰抑制,首先需要确定干扰子空间[11]。而EMP算法是依据式(6)中ρ的值来判断主瓣干扰,在实际中ρ值的选取并没有确定方式[12]。因此,文献[13]中采用干扰特征向量与期望信号导向向量的相关系数来判断,即 (12) 然而当主瓣干扰信号强度与旁瓣干扰相当时,根据信号子空间理论,此时,旁瓣干扰对应的特征向量中包含主瓣方向的导向向量成分,表明旁瓣干扰也与期望信号存在很强的相关性,针对多主瓣干扰,采用选取相关系数的最大值也很容易使得选取的主瓣干扰子空间包含旁瓣干扰。 本文利用文献[14]的思想,将文献[15]方法用于确定主瓣干扰对应的特征向量。对于确定的阵列与期望来波方向,其主瓣宽度可以确定,如对于均匀线阵,主瓣宽度为[13] (13) 式中:N为阵元数目;λ和d分别为波长与阵元间距;θs是期望信号方向。将主瓣范围内所有方向信号积分构成主瓣空间协方差矩阵 (14) 式中:φ表示主瓣的范围,再将其进行特征分解 (15) 其大特征值对应的特征向量Ums可以近似地表示主瓣子空间[15]。利用特征向量与主瓣子空间的正交性来判断主瓣干扰,即 (16) 当ui为主瓣干扰对应的特征向量时,k接近于1,由此可以区分主瓣和旁瓣干扰。 确认主瓣干扰对应的特征向量后,可以依据式(7)确定投影矩阵,然而EMP算法只适合各个信号之间差异较大的情形,文献[7]指出,对于强弱非均匀的信号,其导向矢量可以近似认为与特征向量一一对应,当主瓣与旁瓣信号或目标信号强度相当时,各个特征向量对其余方向的导向矢量的贡献则无法忽略,即不满足 (17) 式中,i,j为不同方向的信号。此时,利用经过特征投影预处理后的协方差矩阵求自适应权矢量会导致在旁瓣干扰处无法产生零陷[16],输出SINR急剧下降。 为解决同时存在强弱主瓣干扰下特征投影法出现的问题,针对不同强度的主瓣干扰采用不同的方式求取干扰对应的特征向量。对于信号强度远小于旁瓣干扰的主瓣干扰,经过采样协方差矩阵特征分解后对应的特征向量可以直接作为主瓣干扰特征空间向量中的向量,对于信号强度与旁瓣相当的主瓣干扰的特征向量,首先采用空间谱估计的方式对其干扰方向进行估计,即 (18) 式(18)采用MUSIC算法对主瓣干扰进行估计,其搜索范围可以限制在主瓣内。在实际环境中,一般认为旁瓣干扰的干噪比较大,因此与旁瓣干扰强度相当的主瓣干扰可以认为是强干扰,其角度估计误差较小。再构建强主瓣干扰特征向量空间为 (19) 式中:I1为强主瓣干扰个数。其特征分解后对应的I1个大特征向量构成的子空间Um i=(um1um2…umI1)作为新的特征向量。综上所述,主瓣干扰对应的特征向量的选取规则为 (20) 式(20)表明,当主瓣干扰远小于旁瓣干扰强度时,特征向量与EMP算法一致,当主瓣干扰与旁瓣干扰相当时,特征向量与空间谱协方差矩阵重构的方式得到的一致。主瓣干扰对应的特征向量的集合为 (21) 即为主瓣干扰的特征向量空间。最后利用式(7)得到投影矩阵,利用式(10)得到自适应权值。 采用半波长间隔、阵元数为17的均匀线阵作为仿真实验对象。图1是固定旁瓣干噪比为40 dB、方向为-25°、主瓣干扰为-4°、干噪比为10~70 dB且由小变大时,经过200次蒙特卡罗实验计算的主瓣干扰对应的特征向量与主瓣子空间的相关性的结果。 图1 主瓣干扰与主瓣子空间相关性 由图1分析可以得到当主瓣干扰与旁瓣干扰强度相当时,主瓣干扰对应的特征向量不仅受到主瓣方向的影响,还包含旁瓣干扰方向上的作用,当对主瓣对应的特征向量进行投影处理时,其对旁瓣干扰方向的导向向量也会进行投影,从而自适应波束形成后对旁瓣干扰方向的抑制也会削弱。 再假设空间内存在3个干扰,其中2个在主瓣内,1个在旁瓣,且主瓣干扰中一个为弱干扰,一个与旁瓣干扰强度相当,快拍数取100,信噪比(SNR)取0 dB时干扰与主瓣子空间相关性如表1所示。 表1 干扰参数 图2是不同算法自适应后的方向图,其中,QUI,SMI,EMP,SC,PRO分别表示静态方向图、采样协方差矩阵求逆算法、特征投影算法、子空间滤波和协方差矩阵重构算法与本文提出的算法运算后的方向图。为了增强系统鲁棒性,所有算法采用了相同的对角加载量。其中,SMI算法在主瓣内形成了两处零陷,破环了主瓣形状,且旁瓣增益变高,与静态方向图差异较大,其他方法均能实现主瓣保形;但EMP算法在强主瓣干扰条件下,在旁瓣处并未形成零陷;SC算法在多主瓣干扰下虽然在旁瓣形成零陷,但其性能明显下降;而本文提出的算法则在同时存在强弱主瓣干扰的条件下表现出很好的性能。 图2 自适应方向图 由于采用的是采样协方差矩阵来代替协方差矩阵,因此快拍数对结果有一定的影响。图3是采用表1所示干扰条件下,经过200次蒙特卡罗实验得到的快拍数、信号与旁瓣干扰的输出SINR的结果。从图3中可以看出:EMP算法在存在强主瓣干扰时性能较差;SC算法性能稳定,但对多主瓣干扰下的结果性能甚至不如SMI算法;SMI算法则由于主瓣变形,使得对信号的增益减弱;本文算法(PRO)则利用了SC算法的优势,解决了在强干扰条件下EMP算法性能下降的问题,并且在多主瓣干扰的条件下表现出比SC算法更好的性能。 图3 快拍数对输出SINR的影响 图4则是比较了在不同输入SNR的情况下输出SINR的结果。不同算法的趋势与理想的曲线近似,在同时存在强弱主瓣干扰条件下,本文算法显然拥有更好的表现。 图4 输入SNR对输出SINR的影响 本文提出了一种根据干扰特征向量与主瓣子空间的正交性分析以及主瓣干扰的相对强度判断来确定主瓣特征对应的特征向量的方法,并由此重构主瓣干扰特征向量空间,再通过特征投影与自适应波束形成算法,抑制了旁瓣干扰并实现主瓣方向图保形。该方法解决了在强主瓣干扰下EMP算法性能明显下降的问题,并且在同时存在一个强主瓣干扰和一个弱主瓣干扰的条件下,相比利用空间谱重构协方差矩阵的方法对旁瓣干扰的抑制效果更优。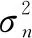
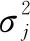
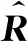
1.2 EMP算法
2 主瓣干扰特征向量空间重构
2.1 主瓣干扰特征向量判定
2.2 EMP算法的局限性
2.3 干扰特征向量空间构建
3 仿真

4 结束语
