基于安全性能的单项竞价交易模式研究与实现

车佳丽,任俊玲

(北京信息科技大学信息管理学院,北京 100192)

0 引 言

大宗商品交易[1-2]作为电子交易的一种，近年来受到了广泛的关注，在隐私保护方面也得到了重视。从安全性能的角度进行分析，一个完善的大宗商品电子交易体系应满足以下要求：1)信息的保密性：交易商的信息、交易指令及其他敏感信息进行可靠加密; 2)交易商身份的确定性：通过可靠有效的技术及管理方面措施，确保交易商身份的正确识别认证; 3)不可否认性：有完善的系统安全、数据备份和故障恢复手段，确保交易数据的安全、完整、准确、不可抵赖; 4)不可伪造性：确保交易商核心信息的安全，相关信息不被不正当的利用。

目前在电子商务领域已经结合了一些密码学知识来保证交易的安全进行，文献[3]采用改进的一次盲公钥和代理签名技术，实现了对消费者隐私信息的保护和对欺诈者的可追踪性。文献[4]提出了一个可保护用户隐私的电子交易方案。该方案将不经意传输协议和ElGamal签名相结合，实现了电子交易中交易双方的隐私安全。文献[5-6]提出了一种基于比特承诺的部分盲签名方案，主要用于提高离线电子现金系统的效率。除此之外，Bit承诺还应用于电子拍卖[7-8]和彩票[9]，以实现整个过程的保密性。在技术方面，文献[10-12]提出了改进的盲签名方案，并验证了其安全性。

当前的安全性研究大都针对普通电子交易，而对大宗商品交易的研究却很少。本文研究的是在第三方认证机构不可信[13-15]的前提下，对大宗商品交易中的单向竞价模式进行分析，引入了盲签名机制[16-18]和Bit承诺协议[19-21]来保证交易的安全性。

1 大宗商品交易模式

在大宗商品交易中，单项竞价是在传统拍卖及竞标的基础上，融合现代电子技术形成的新型电子商务模式。与其他大宗商品电子交易模式的不同之处在于单向竞价交易是指买方在同一时间对某商品竞买或者卖方在同一时间针对某个确定的买方开展的竞卖行为。它在企业与客户之间建立起连接，使交易商双方的参与度达到最高，成为了一种主流的交易模式。单向竞价交易系统适用于稀缺品种的竞拍，或者数量较大的原材料的采购与销售。

单向竞价交易按报价是否公开分为竞价和招标2种形式。在满足其他安全性要求的前提下，招标模式需要保证报价信息的保密性，只有在开标之后才能公开报价。所以本次研究聚焦于招标模式，针对交易流程中存在的安全性问题提出解决方案。招标模式的具体流程如图1所示。

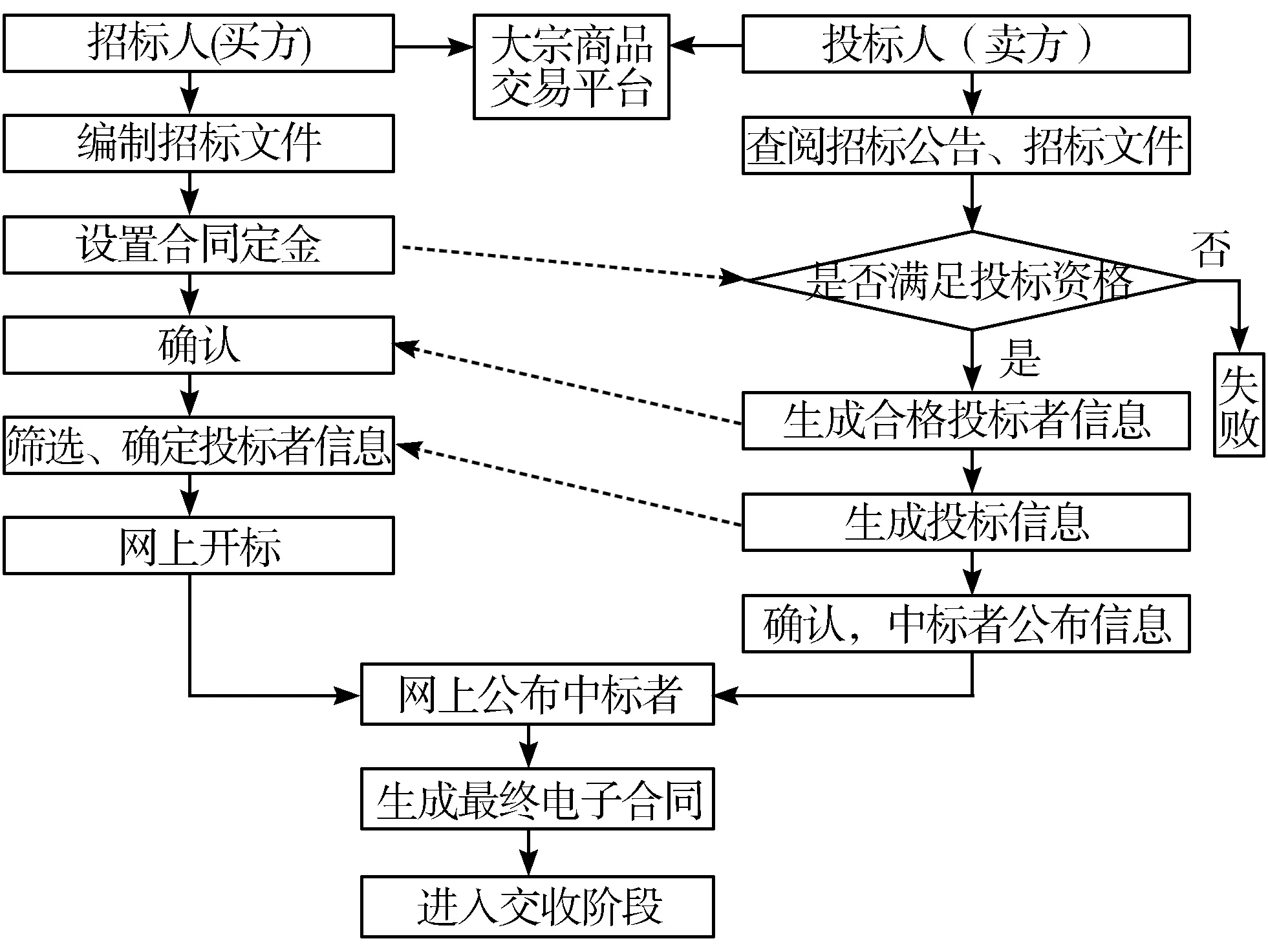
图1 招标模式交易流程图

由投标人和招标人即买方和卖方经大宗商品交易平台注册之后，买方编制招标文件，设置合同定金。卖方经查阅之后确认是否满足投标资格，若不满足则退出此次交易，若满足资格，则生成合格投标者并将信息发送给买方，由买方确认之后再发送具体的投标信息，包括金额、数量等。买方进行筛选、确定投标成功者并开标，卖方确认自己是否中标，达成一致后，网上公布中标者，生成最终合同，并进入交收阶段。

针对招标模式的交易流程对其进行分析，可能存在的安全性问题有：1)如何在第三方机构不可信的前提下，实现交易商身份保密；2)在交易过程中如何保证交易商的报价信息不被泄露，且与身份信息相对应，即保证报价与身份的一致性；3)如何使交易商不能否认其报价。

2 Hash函数

2.1 函数及其安全性分析

Hash函数[22-23]是一种单向函数，它有一个输入和输出，其中输入为任意长度的消息或信息，通过计算，输出固定长度的散列值，而散列值就可以被用来检查消息的完整性。

单向Hash函数是一个满足以下条件的函数H：

1)函数H针对所有人可见，是公开的。

2)要求任意长度的输入x，输出H(x)是固定长度的。

3)函数H单项不可逆，即给定一个x，计算H(x)容易，但是根据指定的输出值y，要想找到一个x使得H(x)=y是困难的；并且找到2个不同的输入，使它们的输出相同是非常困难的。

单向Hash函数的安全性要求如下：

1)抗原像攻击。根据指定的输出Hash值y，攻击者试图计算出输入x是不可行的，即攻击者即使得到消息的散列值，也无法计算出原消息。

2)抗第二原像攻击。用给定的输入x，找到x′使得输出的Hash值H(x)=H(x′)是不可行的，即攻击者无法对消息进行伪造从而得到相同的散列值。

3)抗碰撞性。找到满足H(x)=H(x′)的一对(x，x′)是不可行的，即不存在2个不同的消息，使其散列值相同，保证了消息的完整性传输。

2.2 基于Hash函数的消息认证

Hash函数在认证方面使用询问应答机制，假设通信双方A和B共享通信密钥。通信时，A发起询问并发送一个随机数，B根据随机数和共享密钥来整体计算Hash值H，并把H发送给A，A也计算随机数和共享密钥的Hash值H′，若H=H′，则双方可以进行通信，这样既保证双方的共享密钥安全，也对消息来源进行了验证。

在电子交易中，Hash函数用于解决身份一致性问题，具体应用如下：假设H为单向Hash函数，x为生成的随机数，y为买方B的身份信息，Z为订单信息。首先买方B计算由随机数和身份信息得到的哈希值，然后将其与订单信息一起发送给A，卖方A接收之后减少相关库存信息并给B发送确认信息，之后B将身份信息y发送给A，由A计算哈希值并确认买方B的身份是否与之前的信息一致。

3 盲签名理论

盲签名指的是接收者在不让签名者获取签署内容的前提下对消息进行签名，而签名者恰好对消息的内容不关心，只需要在未来某个时刻验证消息的真实性即可，从而实现认证消息的保密性。

3.1 盲签名算法及其安全性分析

数字签名分为对消息的签名和对散列值的签名，是针对明文进行操作的，而盲签名首先对消息做变换，然后再发送给签名方签名，过程如下：

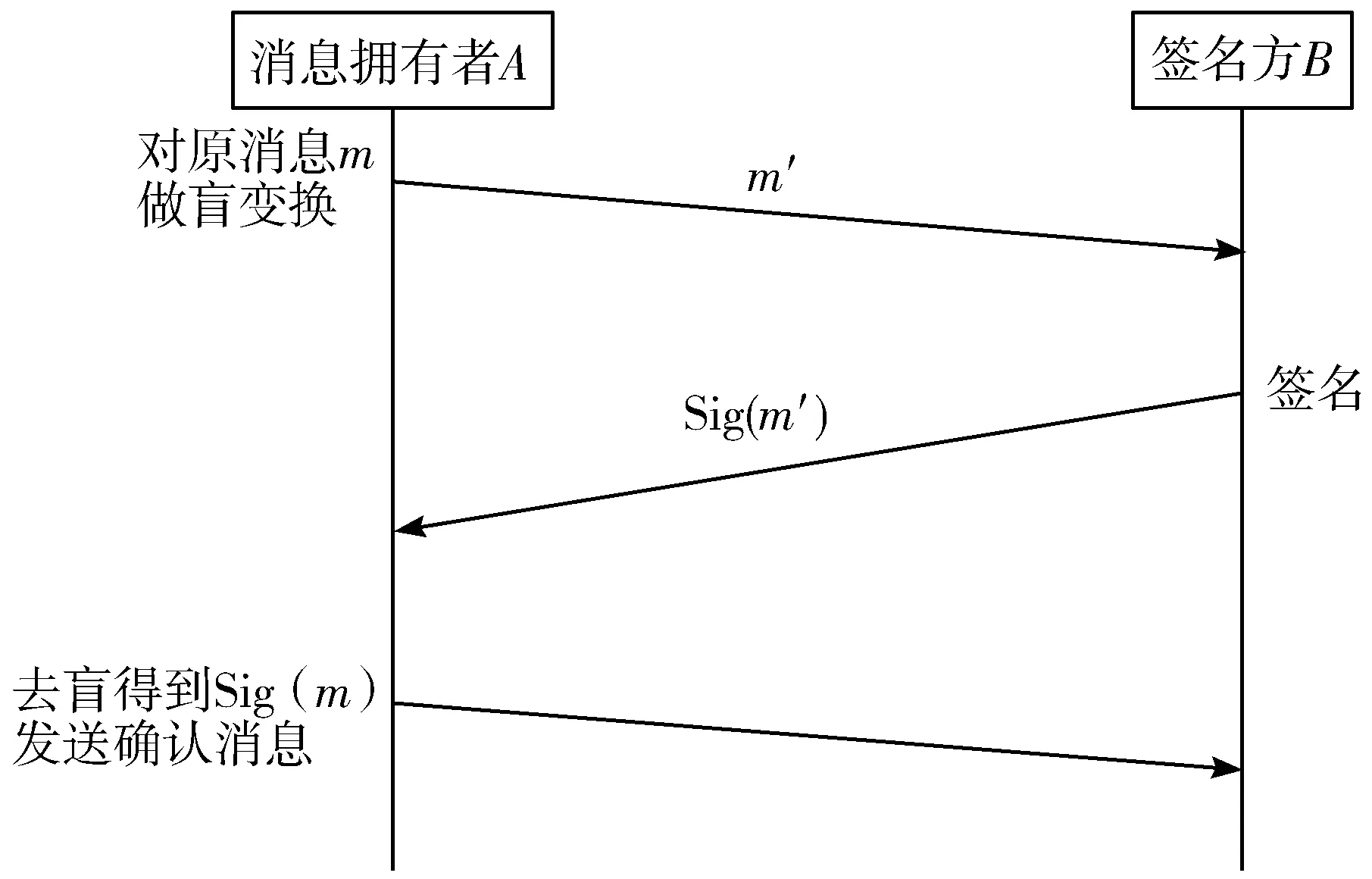
图2 盲签名过程

1)接收者首先对待签名的消息m做盲变换，得到盲化后的消息m′。

2)接收者将盲化后的消息m′发送给签名方，由签名方进行签名。

3)签名方经过签名认证后，将签名消息Sig(m′)发送回接收者，接收者去盲变换后得到对原数据的签名Sig(m)。

4)根据签名满足的数学特性对该签名进行验证，判断签名和信息的准确性。

盲签名的安全性主要体现在2个方面，一是盲性，指签名者对盲化后的信息m′进行签名后得到Sig(m′)，却不能还原消息m，传统的数字签名是针对明文进行签名，因为公钥是公开的，所以一旦私钥被窃取，消息m就会被泄露，盲签名的引入解决了这一问题;二是不可追踪性，签名者不能通过计算得出Sig(m)与Sig(m′)之间的关系，签名者只能对盲化后的消息进行签名得到Sig(m′)，接收方经过去盲后得到Sig(m)。

3.2 基于Schnorr算法的盲数字签名

签名方案中的参数说明如表1所示。

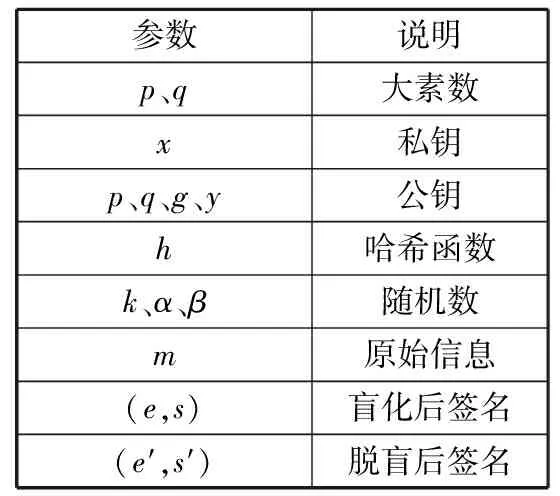
表1 参数说明

签名方案的步骤如下：

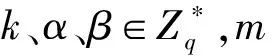
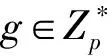
步骤3签名。

1)签名者B随机选择k，计算盲签名因子r=gkmodp，并将盲因子r发送给消息拥有者A。

2)盲化。A选择随机数α、β，计算r′=rg-αn-βmodp，e′=h(r′||m)modq，e=e′+βmodq，并将e发送给签名者B。

3)签名。签名者B计算s=k-ex modq，并将s发给A。

4)去盲。A计算s′=s-αmodq，(e′，s′)即为签名者B对消息m的签名。

步骤4验证。由A计算r′=gs′ye′modp，若h(r′||m)=e′成立，则接受(e′，s′)是对消息m的盲签名。

在电子商务中，用户首先向平台进行注册，然后经第三方机构签名认证后才能开始交易。为了保证身份信息不被泄露，在不依赖于第三方认证机构可信的前提下，可以引用盲数字签名，即对匿名身份信息进行签名认证，由用户脱盲之后得到最终签名。

4 Bit承诺

4.1 Bit承诺协议及其安全性分析

比特承诺是密码学中的重要安全协议，其基本思想如下：发送方A向接收方B承诺一个消息，分为2个阶段:1)承诺阶段，A首先向B承诺要发送消息，但是B无法获知消息的具体内容；2)揭示阶段，A向B证实第一阶段所承诺的消息，但是不能欺骗B。

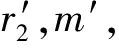
Bit承诺的特点体现在在正式通信前有一个承诺阶段，使得在第2阶段不能进行欺骗，它的安全性体现在：首先是不可否认性，Bit承诺协议保证消息传送者在第1阶段发送承诺消息，在第2阶段不能否认。其次可验证性，根据Bit承诺协议，生成的随机数和单向函数是公开的，所以消息接收者可以对收到的消息计算其摘要验证消息的真实性。

4.2 基于Bit承诺的安全电子交易

电子交易中Bit承诺协议的应用体现如图3所示，在交易开始后，买方首先生成2个随机数，计算随机数和订单信息整体的哈希值，然后将一个随机数和哈希值发送给卖方，经由卖方接收确认之后，买方在第2阶段将另一个随机数和订单信息m发送给卖方，保证了在整个交易过程中，买方对交易订单的不可抵赖性，实现了安全交易。

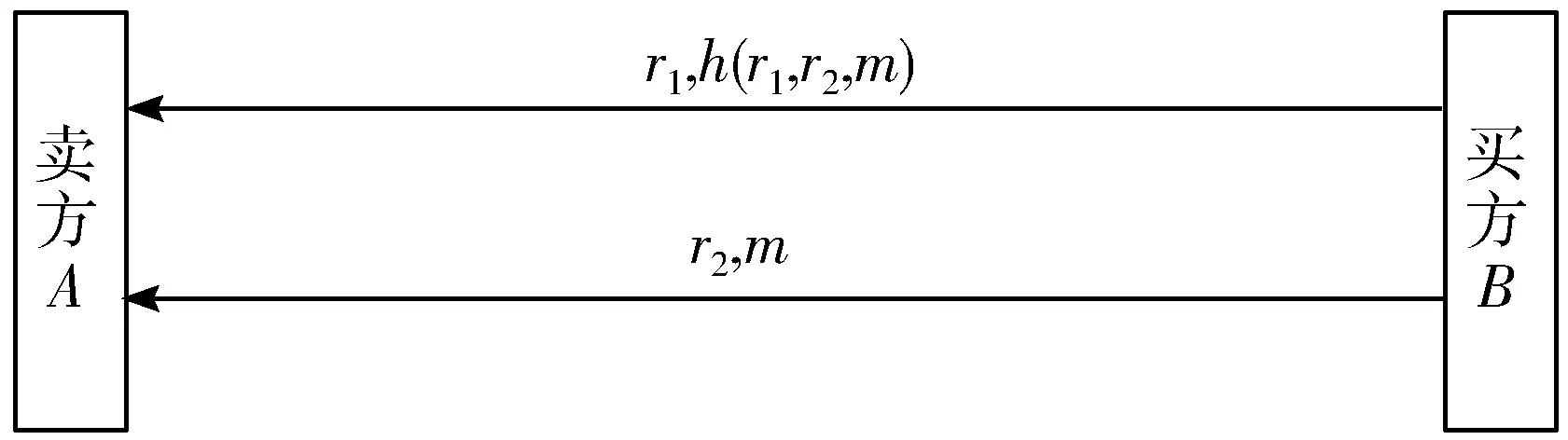
图3 基于Bit承诺的电子交易过程

5 大宗商品交易模式(招标)的改进及安全性分析

针对大宗商品交易中存在的安全性问题，将Hash函数、盲签名、Bit承诺三者相结合，对招标模式进行改进，方案设计如图4所示。

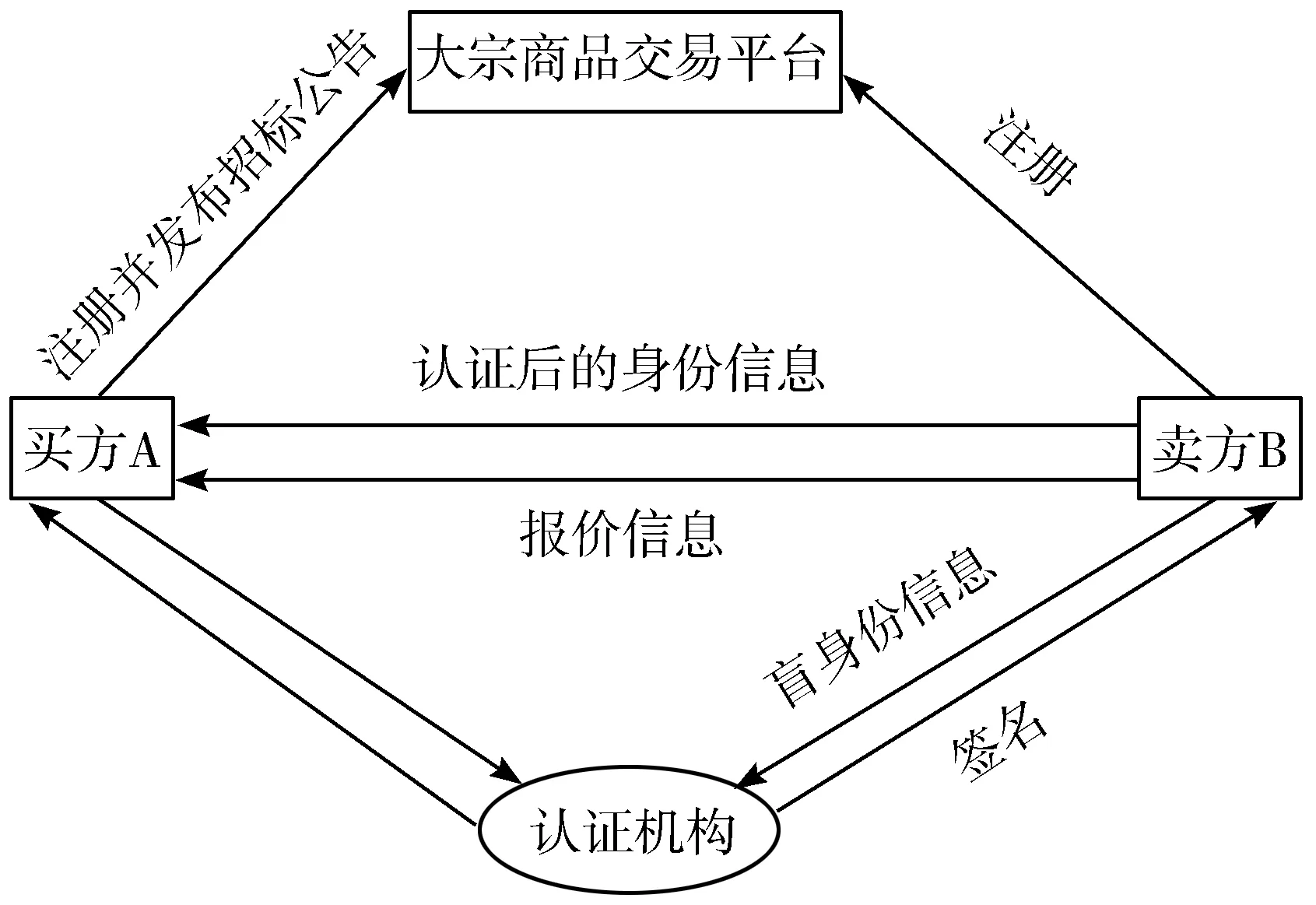
图4 招标模式流程改进图

方案描述：

假设认证机构为不可信赖的第三方，负责登记交易商的身份信息，并进行签名认证。

1)准备工作。

①招标人和投标人即买方和卖方分别在大宗商品平台上进行注册，假设注册身份为Bi(i=1,2,…,n)，由平台查验注册方的身份信息，每一个合法的投标者Bi自己选取一对大随机数(xi，yi)，其中yi为Bi的匿名身份。

②买方A编制招标文件并发布招标公告，包含招标商品的质量、数量和可接受的招标价范围{b1,b2,…,bn}，由大宗商品交易平台进行展示，并公布一个单向函数F(x,y,b)。

③第三方认证机构进行随机数的选择，确认为p、q，然后选取哈希函数h和密钥对，私钥为m，公钥为p、q、g、n。

2)投标者获取盲签名。

①认证机构首先要与被签名的用户建立联系并发送盲因子，根据盲Schnorr签名的定义，CA选取一个随机数，然后利用公钥计算出r，并将盲因子r发送给投标方Bi。

②投标方Bi接收到r后，要对r做变换，选择随机数α，β，然后利用随机数和公钥得到r′，之后用r′对身份信息yi进行盲化，假设盲化后的消息为e，投标方将e发送给CA，进行后续的签名操作。

③CA接收到e之后，对e签名得到s，并将s发给Bi。

④Bi收到的(e，s)即为签名信息，然后对其脱盲，得到(e′，s′)是对Bi身份信息的盲签名。

3)投标阶段。

投标方Bi参与报价，每个Bi只能参与一次报价，设对应为bk(k=1,2，…,n),计算Zi=F(xi，yi，bk)，将(Zi，yi，(e′，s′))发送给买方A。买方A验证投标者的身份信息，计算r′=gs′ne′modp，若h(r′||yi)=e′成立，则接受(e′，s′)是对Bi身份信息的盲签名，从而决定是否接受Bi的投标，并公布合法投标(Zi，yi)。

4)开标阶段。

投标方Bi向买方A发送(xi，yi，bk)，然后买方A验证Zi=F(xi，yi，bk)是否成立，从而判定该投标人发送的bk是否与先前承诺的一致，之后在bki(i=1,2，…,n)中选择最合适的值bk，其对应的匿名身份为yi的即为中标者。

协议结束后，中标者公布自己的(xi，yi，(e′，s′))，A验证中标者身份，然后再进行后续的支付操作等。

安全性及性能分析：

1)保密性。在交易的过程中，yi代表了投标者的身份，交易商和第三方只知道其他交易商的匿名信息yi，无法获得其真实身份信息，实现了身份的保密。在第1阶段，每个投标者向招标方发送经Hash函数计算得出的Zi，并不能确定真实的报价信息，只有在公示合法的投标者之后，投标方才会向招标方发送报价bk，并由招标方确认。即在投标的过程中，A只能获得yi，不能获取bk，实现了对报价信息的保密。

2)不可抵赖性。Bit承诺和单向函数的限制，使得投标者Bi难以伪造一个与其投标价bk不同的bk′，这使得他们满足F(xi，yi，bk)=F(xi，yi，bk′)，所以投标方不能否认其投标价。

3)不可伪造性。标价不能伪造，因为每个投标者都有属于自己的xi且不被其他投标者知道，即使平台泄露yi，如果没有对应的xi，会使得交易无法正常进行。

4)强可验证性。由于单向函数是公开的，开标阶段A公布bk，协议结束后，中标人公布身份信息，任何人都可以验证中标者是否中标，即根据单向函数F()的性质可验证B的身份和投标价。

5)高效性。在通信量方面效率较高。本文方案在各阶段的通信量均为O(n)。计算方面也没有复杂的计算，除在投标阶段的盲签名运算外，就只有单向函数的计算，计算量较小。这也是比特承诺机制运行的优点所在。

6 结束语

本文提出了一个能够有效保护大宗商品交易安全进行的方案，从具体的交易模式如招标模式上看，针对身份认证和信息泄露等问题，采用将盲Schnorr签名与Bit承诺机制结合的方法，使得交易商双方可以使用匿名身份进行认证和交易。通过对方案的安全性分析，可以看出在保密性、验证性、不可抵赖和不可伪造性上，此方案是有效可行的。