基于包络特征的IDC网络自适应流量调控方法

梁运德,陈守明,卢妍倩,李雪武,余顺怀

(广东电力信息科技有限公司,广东 广州 510080)

0 引 言

IDC网络不断优化，网络基础设施也随之升级，网络通信技术的发展、网络设备使用量的增加，令网络中的业务量迅猛增长。国外很多企业将更多的精力放在了用户体验上，追求网络应用上更快的速度，对流量调控问题的研究有了相对成熟的成果，而国内现有的流量调控方法已经不能满足实际网络流量供应和用户需求，如果对流量不限制的话会影响整个服务器的正常运行，因此，文献[1]基于软件定义网络，在获取全网拓扑和流量信息的基础上实现业务流的细粒度管理，并针对目前云架构网络，将SDN集中优化控制，较好地应对云网络中数据传输的多样性问题，提出了一种高确定性流量控制方法。文献[2]为了在流程工业中实现流体物料的远程投加，采用上层优化节点、双信道通信网络和本地控制器对流量进行调节，由此提出了隔膜计量泵流量远程控制方案，基于自适应广义预测，设计了控制方案的分级控制策略并验证了所提出方案的可行性和有效性。

但是经过实践，在日益增长的网络流量条件下，以往的研究方法都无法有效处理吞吐率低和带宽损失率高带来的复杂多变的网络状况，因此针对传统流量调控方法存在的不足，基于包络特征，对IDC网络进行全新的自适应流量调控分析，其创新之处在于本文将基于包络特征获得的流量空间分布数据输入到BP神经网络的输入层中，设定神经网络需要反馈的业务类型，以此为隐含层设置的约束规则，同时在隐含层进行数据处理过程，根据其输出结果完成对流量的调控。

1 IDC网络自适应流量调控方法

1.1 构建IDC网络流量能耗模型

调控IDC网络自适应流量，需要构建一个网络流量能耗模型。假设网络元件h具备速率调节功能，并通过能量曲线fh(v)表征，其中，网络元件h消耗的网络流量，是处理速度v的函数。该函数的计算公式为：

(1)

其中,λh表示不允许被忽视的流量能耗；φh表示网络运行量；α表示承载IDC网络运行的设备承载能力。从网络层面看，fh(v)作为IDC网络中各条链路的代价函数，表示在链路h中，由v单位的数据消耗的能量。此次构建的模型，主要考虑链路对网络流量的消耗情况[3-5]。已知构建该模型需要令该模型保持2种相对状态：全速率的工作状态和零速率的睡眠状态。因此构建该模型时，可以获取到的网络链路如图1所示。

图1 网络链路示意图

根据图1可知，字母表示节点位置，线条表示链路；括号中，左边数字表示链路权重，右边数字表示链路带宽。该网络结构中，存在5个节点7条链路。假设该网络拓扑为IDC网络，已知数据从节点f出发时，需要通过6个单位的业务量，到达节点b，此时链路中消耗的网络流量值相同[6-9]。已知网络中的数据流量分散在图1的链路中，而多个链路之间存在多个网络数据传输方式，因此根据流量使用的基本规则，建立IDC网络流量能耗模型，该模型的流量守恒条件为：

(2)

其中，(i,j)表示数据初始节点；(a,b)表示转折节点；r表示路径长度；g表示流量负载值；ε表示控制参数。利用该条件，实现对IDC网络流量能耗模型的构建。

1.2 基于包络特征获取流量空间分布

数据包络中，包含大量有效网络信息，因此利用构建的模型提取包络特征，获取网络中流量的分布状态。利用高斯回波描述流量信号：

s(t)=γe-β(t-τ)2cos[2πfh(t-τ)+q]

(3)

其中，γ表示幅度因子；t表示时间；τ表示信号到达时间；f(t-τ)表示高斯函数；q表示初始相位。利用流量消耗模型提取包络信息，采用希尔伯特变换方法提取包络特征，在该方法下，信号s(t)的复解析信号定义为：

(4)

φi,j(t)=|κ|-1/2φ((t-p)/κ)dt

(5)

其中，κ表示尺度因子；p表示时间平移因子。将上式写入公式(2)建立的模型中，根据自相似原则提取包络特征，结果为：

T(t)=(2π)-1/2·esωt·e-t2/2

(6)

其中，ω表示流量权值；s表示提取限制。根据公式(6)得到包络特征的实部和虚部为：

(7)

其中，Tu(t)表示实部，Tv(t)表示虚部，ωt表示流量权值。而网络中，流量的分布状态可划分为2种，一种是网络中密度较小流量分布，用虚部表示；另一种则是流量密度较大的分布。互联网数据中心中，一条链路可能存在流速差别极大的数据分布方式，而包络特征就可以利用不同的曲线，来描述网络中流量的空间分布状态[13-16]。

1.3 设置调控的自适应约束规则

根据获得的流量空间分布，设置网络内部信息流向的自适应约束规则。已知IDC网络中，数据流量业务的占比存在较大差异[17-20]，表1和表2是数据流量业务在不同空间内的占比统计结果。

表1 数据流量业务在移动接入端的流量占比

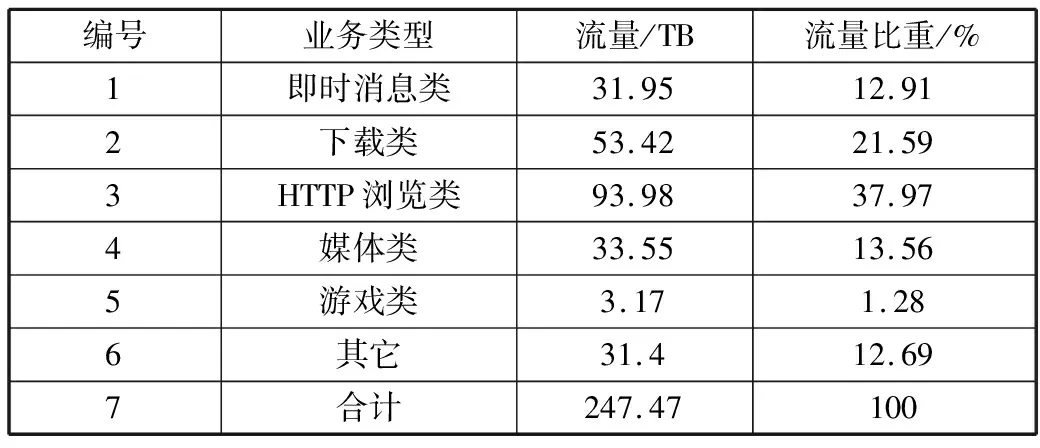
表2 数据流量业务在移动网络中的流量占比

根据流量分布占比统计结果，可知HTTP浏览类与下载类所需的流量更多，因此面对不同类别的内部信息流向，设置自适应约束规则，以此实现对流量调控的自适应约束。考虑流量调控的复杂性，采用随机梯度法中的LMS算法，结合最小均方误差准则，设置约束条件[21-22]。可将最小均方误差准则的目标函数写成：

(8)

其中，ω表示权值；E表示目标函数；xi与yi分别表示第i个业务类型下，网络流量的预计接收信号和干扰信号；c表示业务类型大小。利用该自适应算法设置约束规则：

(9)

其中，Zn表示存在n个变量的权重集合；Bk(ω)表示不等式约束条件；Bs(ω)表示等式约束条件；k、s表示不同类型的调整空间；U、V表示约束条件的集合。通过上述过程，设置网络内部信息流向调控的自适应约束规则，制约调控方法的约束程度。

1.4 BP神经网络调控流量分配方式

已知人工神经网络(BP)具有极强的自适应能力，因此利用BP神经网络，作为调控网络流量分配方式的基本方法。选取的BP神经网络共有3层，即数据输入层、隐含层以及输出层。调控IDC网络流量，将基于包络特征获得的m个流量空间分布数据，输入到神经网络的输入层中，设定神经网络需要反馈的业务类型为d，在隐含层中，依据设置的约束规则，训练分布数据，完成后从输出层得到流量基本分配值。图2为BP神经网络的流量调控方案[23]。

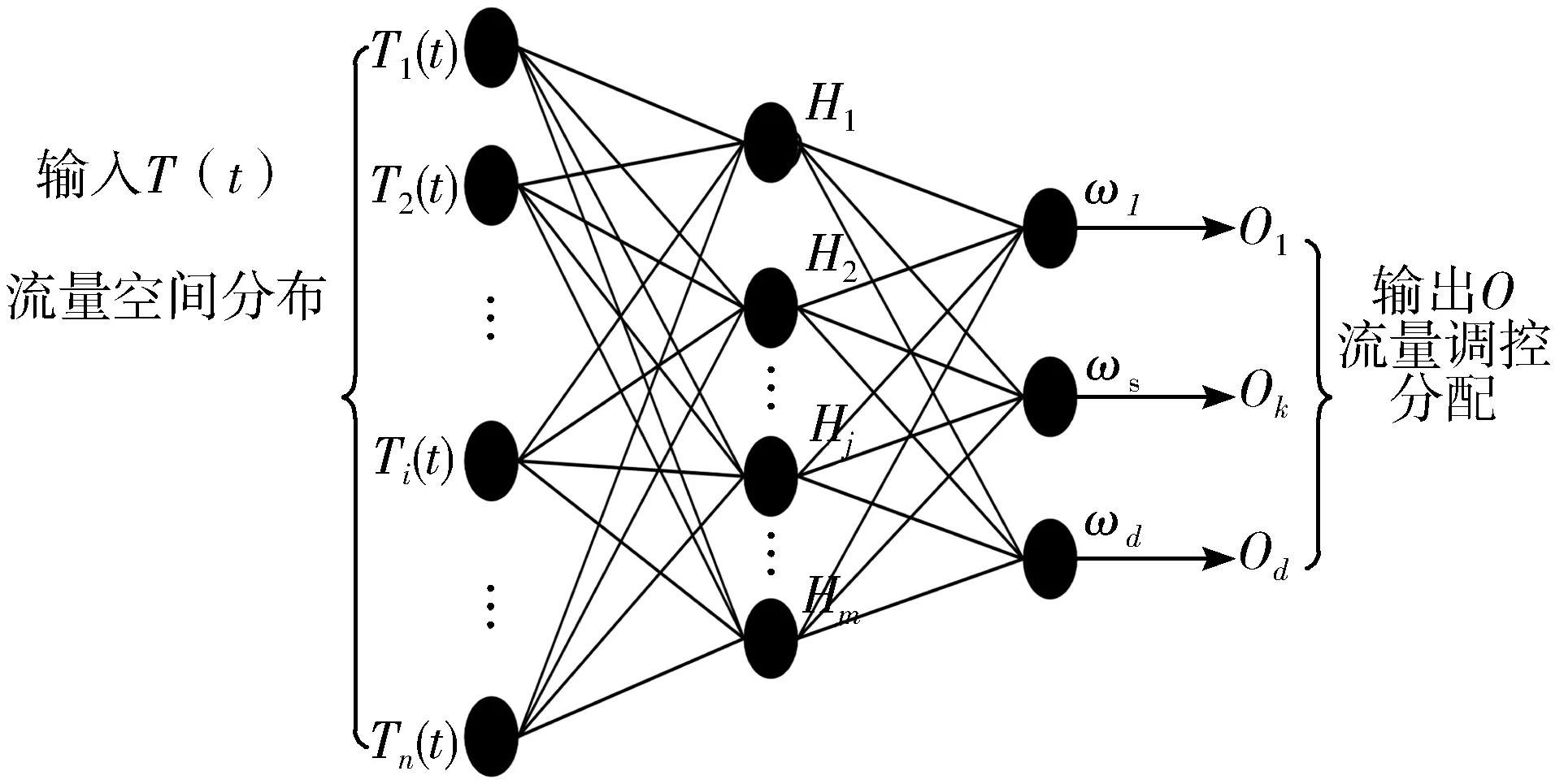
图2 BP神经网络调控方案

根据图2所示，输出阶段的O值，即为流量调控分配的实际结果。但BP神经网络的训练效率稍低，其收敛时间较长，因此根据变化的误差改变网络结构的训练效率，图2中，H值就是改变网络结构后的隐含层的训练效率参数。

假设BP神经网络是W维网络，在其权值空间内搜索最优分配方式的初始化权值，权值数据用d表示。IDC网络空间中，c个粒子组成数据种群F，存在F=(F1,F2,…,Fc)，其中Fi表示第i个粒子在网络空间中的权值位置。令Fi通过神经网络得到的误差，作为分配方式的适应度值。已知第i个粒子的速度为pi，第i个粒子所出现的最佳位置为个体极值；所有粒子出现的最佳位置为数据种群F的全局极值，分别用公式K0=(ki1,ki2,…,kiw)T和KF=(kF1,kF2,…,kFw)T表示。在调控流量最佳分配方式的迭代过程中，第i个粒子根据当前时刻的个体极值K0、种群全局极值KF生成下一时刻的速度参数和位置参数，该迭代过程为：

(10)

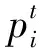
2 实验与分析

为验证此次研究调控方法的性能，本文提出仿真对比实验，将该方法下的实验数据，作为实验组，同时引入文献[1]和文献[2]这2种方法，将这2种方法的实验数据，作为对照1组和对照2组。利用3个方法执行对IDC网络流量的调控任务。

2.1 设置仿真场景

为评估3种调控方法，采用Python编写IDC网络环境作为仿真模型，该模型以数值仿真的形式，模拟网络中流量的生成和链路上的负载。需要注意，由于流量调度方法，是通过改变流量在网络中交换机之间的转发路径来实现负载均衡的，因此使用下面模拟的网络场景时，只关心模拟网络中各台交换机之间的链路负载，不考虑主机与接入交换机之间的链路。模拟的网络场景是一个3层Fat-tree结构的仿真网络，用来模拟数据中心网络环境。该网络包括2个Pod，8台主机，12个交换机，将交换机分为3组，第1组为接入层交换机，第2组为汇聚层交换机，第3组为核心层交换机。令每一组中的交换机数量为4，共16条链路，每条链路的带宽容量为1 Gbps。

2.2 设置网络流量模式

由于数据中心网络中的流量数据很难获取，因此基于随机流量模式模拟仿真网络中的流量。在一个指定范围内随机生成流的带宽需求，并让该随机过程服从均匀分布。实验测试规定网络中所有流量带宽需求大于最小链路带宽容量的10%，将此类流默认为大象流，在设置的模拟网络中，流的带宽需求最小值设置为0.1 Gbps。为了检验网络中调控方法的变化情况，将产生的流带宽需求最大值设为一个变量，即从0.1 Gbps开始不断变化，增大至1 Gbps。已知随机值服从均匀分布，因此认为此时网络所有流的期望带宽需求为5.5 Gbps。

设置流量模式后，还要设置网络中的流量密度。此次在实验模拟的仿真网络环境中，通过控制网络中一台主机向其他主机发送流量的概率，以此控制网络中流的密度。实验设置了3种流量密度，以此为测试变量来对比不同调控方法对网络流量的调控效果。3种实验测试条件如下所示：

1)random20。主机以20%的概率，向其他主机发送流量。

2)random40。主机以40%的概率，向其他主机发送流量。

3)random60。主机以60%的概率，向其他主机发送流量。

上述实验测试条件，分别对应网络流量密度较低、密度一般、密度较高的情况。在模拟的网络环境中产生实时网络流量带宽需求信息，模拟真实网络中流量控制模块执行调控任务时网络的实时带宽需求状态。

2.3 设置实验评估指标

为得到更加具体的实验结果，将吞吐率和网络流量带宽损失率，作为此次实验对3种方法的评估指标。网络流量带宽损失率的计算公式为：

P=M/N

(11)

其中，M表示所有流量带宽损失之和；N表示所有流量需求带宽之和。测试条件准备完毕后，开始实验。

2.4 吞吐率测试结果

测试3种流量调控方法下，不同流量密度中的吞吐率，其结果如图3所示。

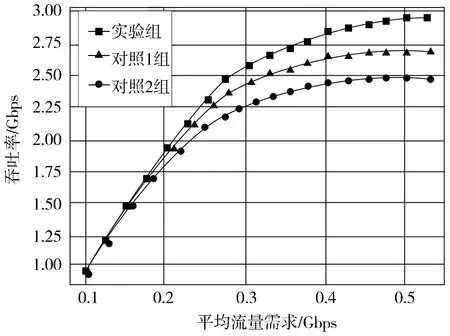
(a)random20流量密度

从图3可以看出，随着流量平均带宽需求的增加，3种方法在网络中的吞吐率，均呈现先增加后平缓的变化趋势，但根据曲线趋势可以明显看出，实验组获得的吞吐率，比对照组的获得结果更高。

2.5 网络流量带宽损失率测试结果

再测试不同流量密度下，3种方法的带宽损失率，其对比结果如图4所示。

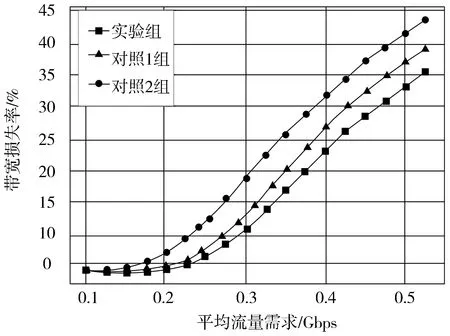
(a)random20流量密度

已知网络带宽损失率越低，则调控方法的性能越好，且网络带宽损失率会随着平均流量带宽需求的增加而不断上升。根据图4可知，3种流量密度下，本文的调控方法，其带宽损失率最低，对照1组的带宽损失率居中，对照2组的带宽损失率最高。

综合上述实验测试结果可知，本文流量调控方法，比文献[1]和文献[2]的方法更符合流量调控要求。

3 结束语

本文提出的流量调控方法，创造性地使用了包络特征，通过设置自适应能力更强的约束规则，获取更加有效的流量调控方法。但此次实验分析较为单一，还应模拟一个更加复杂的网络环境，并在该环境中，同样测试random20、random40、random60条件下，不同方法的带宽损失率，为测试结果提供更加可靠的说服力。