基于集成模型的超短时负荷预测方法

魏 健,赵红涛,刘敦楠,加鹤萍

(1.华北电力大学数理学院,北京 102206; 2.华北电力大学经济管理学院,北京 102206)

0 引 言

短期负荷预测是提高预测精度和保障电力系统正常运行的关键因素[1]。目前对于地市级的负荷值来说，其负荷值的变化受多种因素的影响[2]，许多单一的算法难以胜任较为复杂的预测。

目前应用于短期及超短期负荷预测的机器学习方法有支持向量机、人工神经网络以及一些决策树集成模型，这些模型均各有优势，然而也存在些许不足。如支持向量机处理大规模数据困难[3]、神经网络如LSTM、RNN等典型方法在输入序列过长时容易丢失序列信息[4]，决策树集成模型有时存在过拟合现象[5]。

文献[2]和文献[4]介绍了LSTM算法在短期负荷预测中的应用，LSTM中门的设置很好地弥补了RNN算法梯度消失的现象。文献[6]介绍了CNN-LSTM(Convolutional Neural Network-Long Short-Term Memory)模型，CNN模型可对原始数据抽取特征和降低噪声，进而将处理后的数据输入LSTM处理，在很大程度上解决了LSTM模型输入序列过长时梯度消失的情况。文献[7]介绍了Catboost模型在进行短期负荷预测的优势，说明了基于决策树算法的集成模型学习能力、对数据的分析与处理能力强。文献[8]考虑到集成预测模型的优势，使用主成分分析来确定各个指标的权值。文献[9]和文献[10]使用了BP神经网络(BP Neural Network)确定各个指标的权重，本文尝试使用此方法实现超短时负荷预测。文献[11]表明，集成预测模型可能得到比单项预测模型更好的预测结果，减少预测的系统误差，从而能将各个模型的优势结合起来，显著改进预测效果。

上述文献中使用了多种机器学习算法来进行负荷预测，尤其以神经网络模型和决策树集成模型居多，但是2种模型均存在一定的劣势。单独依靠某种算法可能并不能反映出负荷值复杂的变化规律[12]。而集成模型可以将几种模型的优点通过权重系数巧妙地结合起来，产生更好的效果。

在单项预测模型的选择上，本文考虑CNN-LSTM模型结合了CNN和LSTM的优点，很大程度上克服了输入序列长度过长而导致的梯度消失现象[6]；此外，决策树集成模型学习能力强，泛化能力好，Catboost和Extratrees模型是对随机森林模型的改进，是决策树集成模型的典型代表。所以本文选用上述3种模型作为单项预测模型。

本文采取的集成预测方法，选用Catboost、CNN-LSTM、Extratrees模型的预测值作为输入变量，其真实值作为期望输出值。通过BP神经网络训练得到输入层与隐含层、隐含层与输出层的权重系数[13]。

1 3种单项预测模型

1.1 Catboost

Catboost算法是一种改进的梯度提升树(Gradient Boosting Decision Tree, GBDT)算法，是一种基于提升方法(boosting)的算法，在boosting的基础上加入了梯度下降运算[14]，即每一次建立回归树都利用前者回归树的信息，向以前决策树的梯度下降方向运算。与GBDT算法不同的是，Catboost采用对称树，获取梯度的无偏估计，进而进行梯度下降，由此缓解了过拟合的现象。Catboost在训练过程中用前一棵树学习样本数据，后一棵树根据以前树的信息改变权值，使残差大的树获得比较大的权值。最后，整合多个弱回归器的结果，进而组成学习能力较强的回归器[7]。

与GBDT算法计算不同的是，Catboost算法在GBDT的基础上能够更好地处理分类型特征(categorical features)[15]。处理方式如式(1)：

(1)

其中，p为先验项，α为权重系数。图1为Catboost的流程示意图。

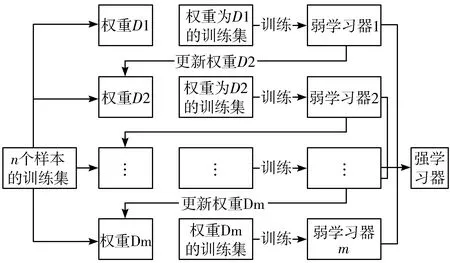
图1 Catboost算法流程示意图

1.2 CNN-LSTM

利用CNN抽取原始数据特征，抽取不同数据维度之间的关系[8]，消除其中的不稳定因素，而后将信息输入至LSTM，LSTM学习数据中的时序特征，从而在很大程度上解决了LSTM间隔时间较长而忽略相关信息的劣势。CNN-LSTM模型具体算法流程如图2所示。

图2 CNN-LSTM集成模型算法流程

首先将经过数据预处理的数据输入卷积神经网络，卷积层中的卷积核负责提取数据特征。池化层通过过滤不重要信息来加强重要信息，经过Flatten层，将经过卷积层和池化层处理的数据构造为特征向量形式输入进LSTM层。LSTM层可以学习时间序列之间的关联[9]，学习特征内部的变化规律。之后连接Dense层，Dense层负责进一步学习数据中隐含的特征，起到加强学习的作用。神经网络虽然功能强大，但是会遇到过拟合等情况，所以使用Dropout的方式来降低过拟合[10]的程度。

1.3 Extratrees模型

Extratrees是一种集成学习算法，包含众多决策树[11]。算法的最大特点是在分裂特征的选择上采用随机的方式，随机选择某个特征的某个取值作为该特征的分裂点。由于具有这2个随机性特点，因此Extratrees算法学习能力较强。在模型学习阶段，为了减少每个弱分类器的偏差，每棵树都利用整个训练样本进行学习。在分割树节点时，极端随机森林对于分裂特征和分割值的获取具有极强的随机性[16]。

Extratrees模型的计算，由一组回归决策子树h{(x,θt),t=1,2,3,…,n}构成，取各决策树{h(x,θt)}的均值作为回归预测值，如式(2)：

(2)

Extratrees模型具体算法流程如图3所示。

图3 Extratrees模型流程图

2 集成模型

2.1 模型介绍

集成模型预测是提高预测精度的最佳方法之一[17]，其中最为重要的是对于权重系数的估计。本节以Catboost、CNN-LSTM、Extratrees模型作为单项预测模型，采用BP神经网络确定权重系数。使用BP神经网络可以通过反向传播算法调节神经网络各层的权重系数，一旦有新的数据出现也可再次调整权重系数，从而寻找最优值，而这是其它权重确定方法无法相比的。

BP神经网络是20世纪八十年代提出的一种算法[18]。BP网络在输入层与输出层之间增加多层隐含层以加强学习，每一个隐含层可以有若干个神经元。因本文研究预测算法，故其输出层只设置一个神经元。BP神经网络的结构如图4所示。

图4 BP神经网络结构图

2.2 集成预测模型权重计算方法

设输入向量为(x1,x2,…,xm)T，隐含层包含k个节点，输出变量为(y1,y2,…,yk)T。其中，输入层和隐含层的权重用矩阵A表示，A=(aij)m×k。隐含层和输出层的权重由矩阵B表示，B=(bij)k×n。经过BP神经网络计算输出的向量设为D=(d1,d2,…,dn)T，真实值为R=(r1,r2,…,rn)T。

隐含层输出如式(3)：

(3)

输出层输出如式(4)：

(4)

设神经网络的某个神经元的真实值和输出值的差值为Ei，从而得到：

(5)

总误差可表示为：

(6)

计算出真实值与实际值的误差后，需要对误差反向传播以更正权重系数[19]。反向传播是由输出层输出d与真实值o相比较得到的误差信号δ0决定的，各隐含层神经元的权重系数根据δ0进行调整；而后将误差信号δ0反向传至隐含层，得到隐含层的误差δyj，由此对输入层与隐含层间的连接权进行调整[20]。调整公式如式(7)～式(8)：

δ0=(d-o)o(1-o)

(7)

δyj=δ0zjyj(1-yj)

(8)

BP神经网络确定权重系数的流程如图5所示。

图5 本文模型确定权重流程示意图

3 算例分析

在对某省A市的电力负荷值预测中，共使用有效数据56420条，时间跨度为2013-03-21—2019-09-24，输入维度包括前一小时的温度、湿度、风向、风力、雨量、负荷值，期望输出值为后一小时的负荷值。负荷值数据每小时记录一次，其中部分数据缺失。本文以前一小时的温度、风力、风向、雨量和负荷值作为特征，以下一小时的负荷值作为标签。在选取训练集和测试集的过程中，为了减少季节因素的影响，本章将2013—2019年中每年9月的数据作为测试集，其余数据作为训练集。本文采用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方根误差(Root Mean Square Error, RMSE)、均方误差(Mean-Square Error, MSE)和拟合优度(Goodness of Fit，R2)来测评模型预测的误差[21]，其中MAPE、MSE、RMSE表达式分别如式(9)～式(11)：

(9)

(10)

(11)

3.1 数据预处理

本文原始数据存在一些缺失值，鉴于缺失值的数量比较少，所以本文采用直接删除缺失值[22]的方法。此外，为了更方便对数据进行训练，本节先采用归一化的方式处理数据，训练结束后再使用反归一化的方式恢复原数据和预测值。归一化处理的算式如式(12)：

(12)

3.2 关键参数调节

3.2.1 Catboost参数调节

本文使用固定参数法来调节Catboost模型的参数，其中影响Catboost模型精确度最重要的2个参数是iterations和depth[23]。iterations为迭代步数，depth为建立决策树的层数。随着三者数值的变化，模型的表现效果往往会先变好后变差[24]。这是因为随着参数数值的增加，模型的学习能力也会增强，但是当超过某一个范围时，就会出现过拟合现象，模型表现的效果反而不尽人意。以下给出Catboost主要参数变化和MSE的关系图。

由图6可得，随着各指标数字的增大，MSE先增大后减小。经过上述实验对比，在Catboost模型中，设置iterations=95，depth=3。

图6 Catboost主要参数与MSE关系

3.2.2 CNN-LSTM参数调节

CNN-LSTM模型中需要调节的参数有很多，如CNN层数、训练步数、LSTM神经元个数等。在这些参数中，以选取卷积层数和训练次数为例来分析参数的调整和MSE的关系，以此方法来寻求各个参数的最优值。

在图7中，在使用CNN-LSTM模型预测负荷值的过程中，应设置1层CNN层，其中卷积核设定为15个，stride=1。设置2层LSTM层，每层设定16个神经元。使用2层Dense层，神经元数量设置为16个。训练次数设定为400次，batch_size=50000，选用adam作为梯度下降法。

图7 CNN-LSTM主要参数与MSE关系

3.2.3 Extratrees参数调节

影响Extratrees模型精确度最重要的2个参数是n_estimators和random_state[25]，其中，n_estimators为建立的决策树的个数。图8为n_estimators和random_state与MSE的关系图。

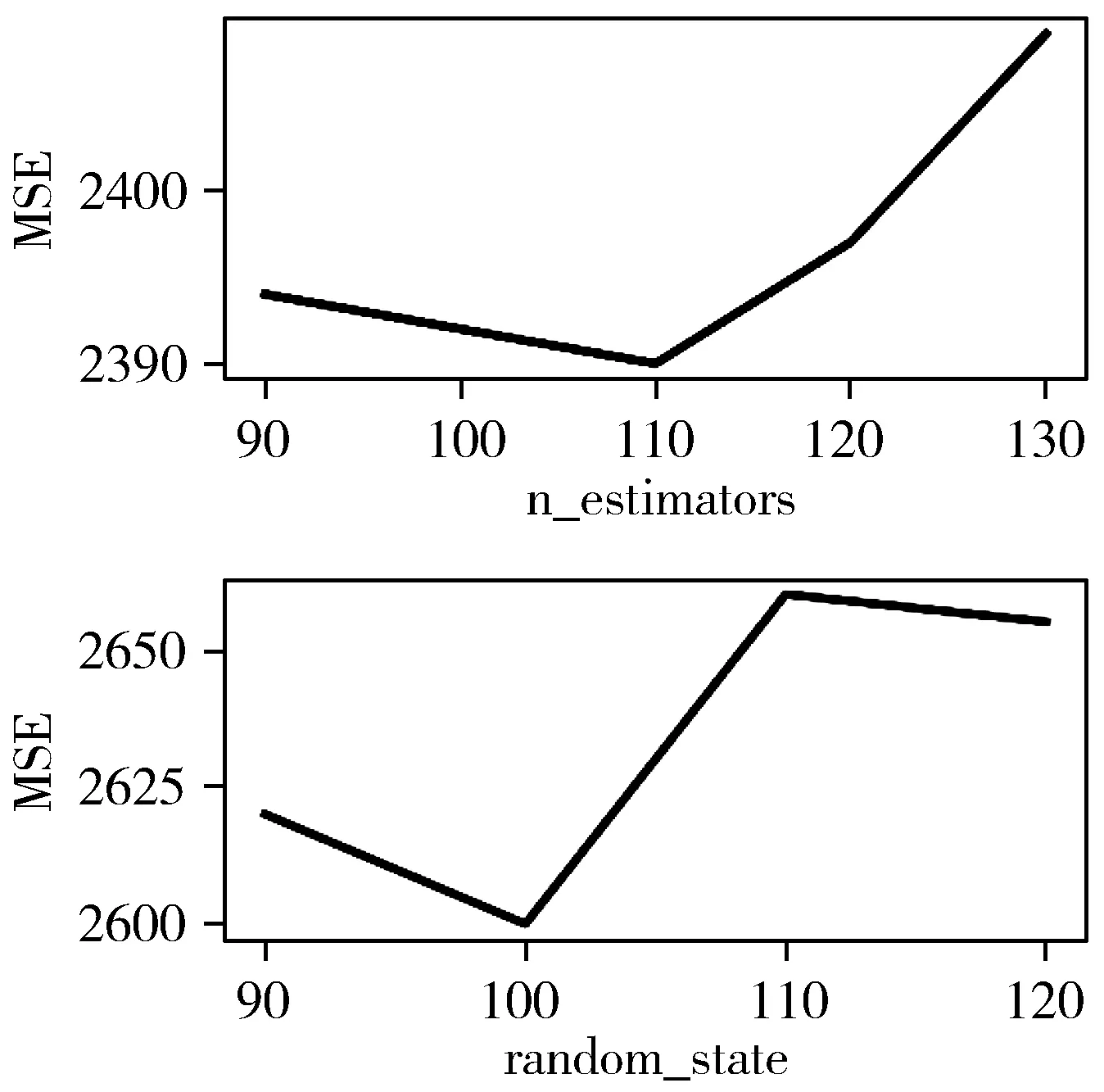
图8 Extratrees主要参数与MSE关系图

从图8中得到，在使用Extratrees模型预测负荷值的过程中，应设置n_estimators=110,random_state=100,min_samples_split=2,min_samples_leaf=1。

上述3种方法均为构建集成模型的单项预测模型，调节参数使得误差结果尽量小，从而更加精准地使用集成模型预测负荷值。

3.2.4 集成模型参数调节

本节将2013—2019年中每年8—9月的Catboost、CNN-LSTM、Extratrees算法的预测结果作为输入变量，将2013—2019年中每年8—9月的负荷值作为标签。在上述数据中将8月的负荷值作为训练集，9月的数据作为测试集，测试集总共有4976个数据点。

本节使用BP神经网络来整合权重系数。影响BP神经网络精确度的主要有训练步数、batch_size等，下文将以MSE为标准，尽量得到各个参数的最优值。

在图9中，在使用Extratrees模型预测负荷值的过程中，应设置2层Dense层，神经元数量设置为10个。训练次数设定为600次，batch_size=600。图10给出了各个单项模型和集成模型预测值与真实值的对比图。

图9 集成模型主要参数与MSE关系图

(a)Catboost预测值与真实值对比

从图10可知，集成模型对于负荷值中极值的预测效果要比单项预测模型优秀，且明显拟合程度更好。Catboost、CNN-LSTM、Extratrees模型虽然也可以拟合出负荷值的走向，但是很显然三者在预测负荷值极值点时效果较差，且对于突变点的预测并不太准确。表1给出了各个模型和集成模型的误差值对比。

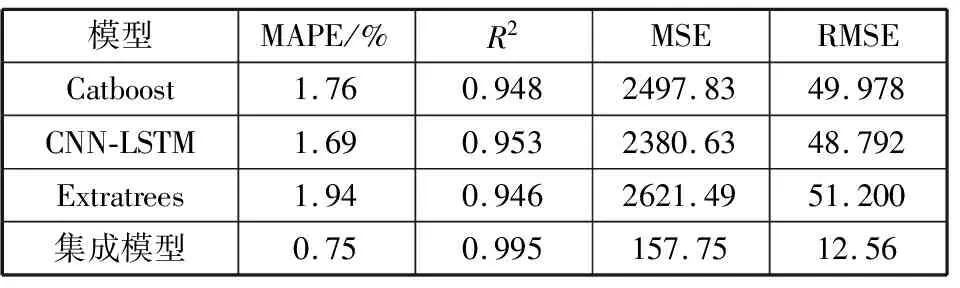
表1 集成模型与各模型误差对比

由表1可知，集成模型在MAPE的标准上比Catboost、CNN-LSTM、Extratrees模型降低了1.01个百分点、0.94个百分点、1.19个百分点。在其它各个标准方面集成模型相比较其它单项预测模型也具有一定优势。

4 结束语

本文提出了以Catboost、CNN-LSTM和Extratrees为单项预测模型，以BP神经网络确定权重系数的超短时负荷预测法，该方法通过权重系数将3个单项预测模型方法结合在一起，从而集合其各种模型的优势，以更好地进行预测分析。本文的集成模型在MAPE、R2、MSE、RMSE方面均优于3个单项预测模型，这表明了本文提出的超短时预测模型有更高的负荷预测精度，但是本文尚未考虑关于气候地形和城市发展程度不同对预测所造成的影响，这将会在以后的研究中加入其中。