面向纸板三维装箱问题的剩余空间最优算法

王 程,陈正鸣,吕 嘉

(河海大学物联网工程学院,江苏 常州 213022)

0 引 言

瓦楞纸板由于绿色环保、可再生以及具备较好的缓冲功能等优势，被广泛用于包装领域，是现代包装领域中用的最多的包装材料，中国也是瓦楞纸板的最大产量国。纸板生产企业除了在生产工艺上进行改善优化，还要在配送环节中避免产品损失。如果装载利用率过低，会使企业的运输成本大大增加。同时，因为不合理的装配或者挤压，容易发生变形和损坏，从而会影响瓦楞纸板的质量，造成浪费和经济损失。所以在保证最大容积装载的同时，减少在物流运输过程的损失也是纸板生产企业所面临的重要挑战之一。

三维装箱问题是研究多种多样的纸板在满足约束的情况下，被装入到某个容器中去，以达到容器的空间利用率最大或使用数目最小等目的，是广泛地存在于实际生活中的复杂组合优化问题。针对不同的情况和需求，学者们提出了不同的求解算法。Huang等[1]提出了一种应用在三维装箱领域上的拟人穴度算法；Eley[2]提出了同构块的概念，实现了一种启发式树搜索的算法；那日萨等[3]通过空间切割实现装箱体积利用率最大，提出了一种启发式搜索法；尚正阳等[4]将三维问题转化为带有高度约束的二维问题，不需要预处理和最优解的搜索，提出了一种高效的启发式剩余空间最优化算法；李孙寸等[5]通过随机放置和局部调整逼近最优解，提出了一种多元优化的算法；张德富等[6]基于块装载的思想，生成复合块，提出了一个高效求解三维装箱问题的多层启发式搜索算法；何鲲等[7]对求解三维装箱问题的穴度算法的基础进行了改进，提出了基于动作空间的确定性高效率求解算法。在求解考虑基本约束的三维装箱问题上，以上的研究都实现了很好的装载效果。但是针对于实际应用上的约束考虑较少，且部分算法求解速度较慢，计算复杂度较高。

因此，本文以容器空间利用率最高和使用数目最少为目标，考虑纸板装箱过程中遇到的多个实际约束，建立一个三维装箱问题的多目标模型，提出一种基于剩余空间最优和实际约束的快速算法对其进行求解。

1 问题描述

本文将装箱问题定义为，把n种数量有限的规则的纸板完全装入一种尺寸为L×W×H的长方体容器A中，M和V分别作为容器A的额定载重量和容积，ni、li×wi×hi、mi分别作为第i种纸板的数量、尺寸和重量。求将所有纸板都装入容器中，并实现容器的空间利用率最大和使用数目最小的目标，并满足多种多样的现实约束，并建立如图1所示的空间直角坐标系。

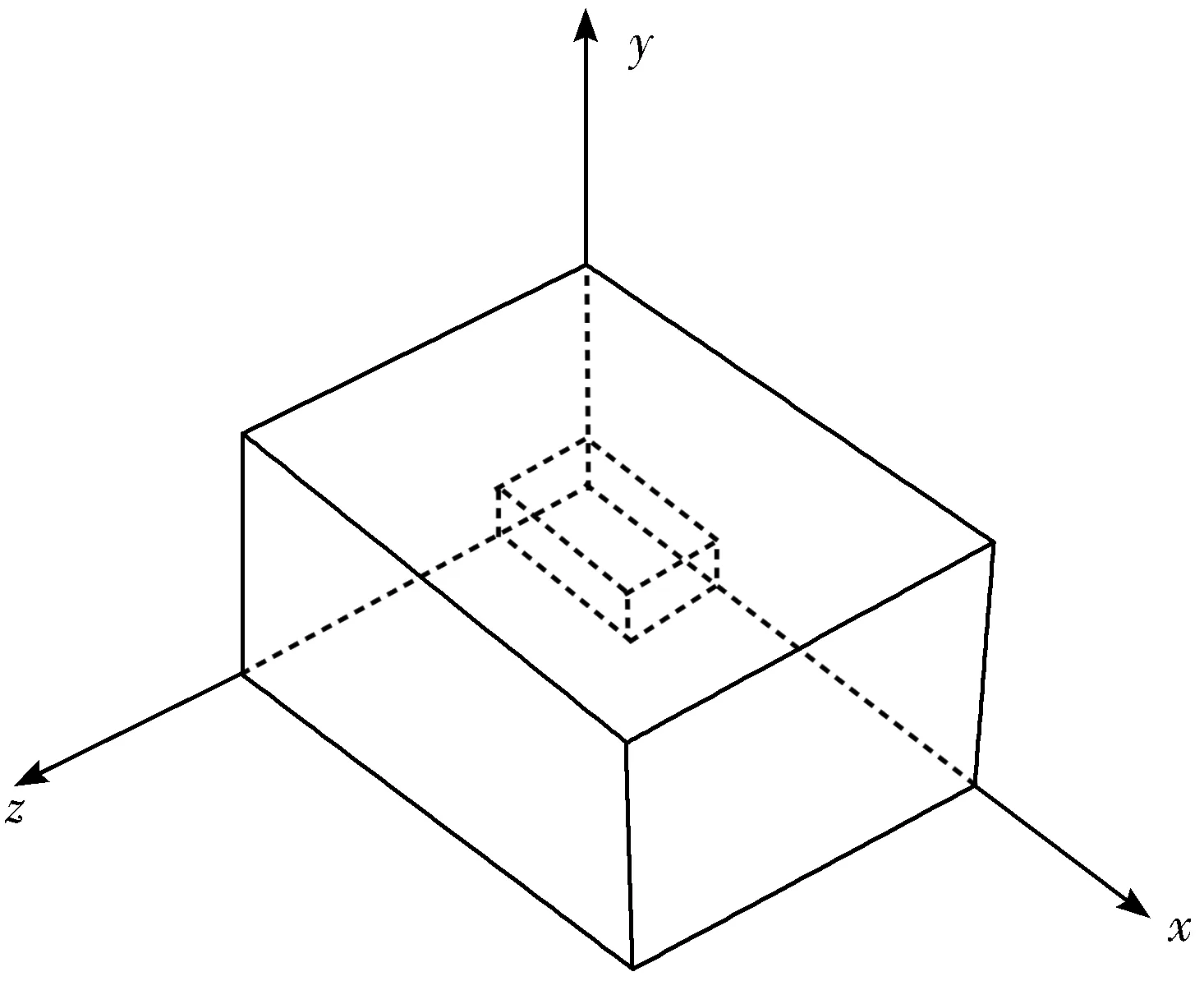
图1 装箱示意图

在装载纸板之前，为方便计数和打包，先将同类纸板按照一定的张数打包成捆。本文在装载纸板时，考虑的瓦楞纸板实际上是一捆纸板形成的纸板集合块，且纸板在实际的装箱中约束条件如下：

1)C1：单个纸板约束。纸板为规则的长方体，且它的长、宽、高和重量都在容器所提供的范围内。

2)C2：纸板的摆放方向约束。放置纸板时，保持与容器边缘平行，摆放方向采用水平方向上的2种。

3)C3：纸板的稳定性约束。在放置纸板时，不能将其悬空。

4)C4：纸板的先进后出约束。考虑纸板的卸载顺序，后卸载的纸板先进行装箱，先卸载的纸板后装箱。

5)C5：纸板的合并装载约束。同一客户的纸板要进行合并装载，并放置在容器中的相邻位置。

6)C6：纸板的堆放约束。在堆放纸板时，考虑纸板的承重级别，承重级别弱的纸板不能堆放在承重级别强的纸板之下。

7)C7：纸板的最大堆放层数约束。纸板在堆放时，为了防止其变形和挤压，限制纸板不超过最大堆放层数进行堆放。

8)C8：容器约束。装载在容器内的纸板的总体积和总重量必须不大于容器的额定容积和载重量。

本文根据上述约束条件建立模型并设计装箱规则。

2 模型建立

设置相关的变量和符号如下：

1)Lk,Wk,Hk,Mk,Vk分别表示容器k的长、宽、高、载重量和体积；(Xk,Yk,Zk)表示k的重心坐标；k为容器的编号(k=1,2,3,…,k)；(a′k,a″k),(b′k,b″k),(c′k,c″k)表示k的重心范围。

2)(pt,qt)表示客户t的坐标，可计算得到客户与配送中心的距离dt；t为客户的编号(t=1,2,3,…,t)。

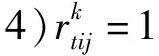
基于多种实际约束的三维装箱模型见式(1)～式(13)。

约束条件：

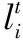
(1)

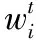
(2)

(3)

(4)

或

其中:

i>0,j>0

(5)

(6)

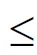
(7)

(8)

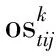
(9)

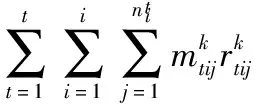
(10)

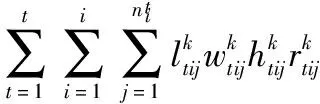
(11)

其中，式(1)～式(4)表示单个纸板约束C1，纸板的尺寸和重量不能超过容器允许的范围；式(5)和式(6)表示纸板的摆放方向约束C2，即纸板的摆放方式只有水平方向的2种；式(7)表示纸板的稳定性约束C3，当纸板b放在纸板i上时，其底面积要不大于纸板i的底面积，放置时不悬空；式(8)表示纸板堆放约束C6，当纸板b放在纸板i上时，纸板i的承重级别不小于纸板b；式(9)表示纸板的最大堆放层数约束C7，表示纸板的堆放层数不能超过纸板本身的最大堆放层数；式(10)和式(11)表示容器约束C8，纸板的总体积和总重量不能超过容器的容积和载重量。

目标函数：

(12)

(13)

式(12)表示容器的容积利用率最大；式(13)表示容器的装箱率函数，N为使用容器的个数，Fk为容器k所装载纸板的总体积，Vk为容器的额定体积。

3 算法设计

3.1 装箱序列的确定规则

在进行装箱之前，对纸板进行组合和排序，确定装箱序列。

1)考虑纸板先进后出约束(C5)，根据客户所在位置计算出客户与公司的距离，根据距离远近确定装载顺序，距离远的优先级高于距离近的优先级，则先进行装载。属于同一客户的纸板，考虑其底面积和承重级别，对纸板进行从大到小的排序，这样能有效地提高一定的空间利用率。

2)考虑纸板组合装载约束(C4)，并满足纸板最大堆放层数约束(C7)，按照相同的摆放方向将同类纸板进行堆放组合，同时纸板在装载前，生产企业会将纸板以一定的张数打包成捆，以捆为单位，生成复合块，将其视为一种新的待装载物品；客户的不同类纸板装载在相同的容器，并保持装载位置相邻。

根据以上规则，对待装载的纸板货物序列进行处理优化，生成符合规则的装箱序列。复合块示意图如图2所示。

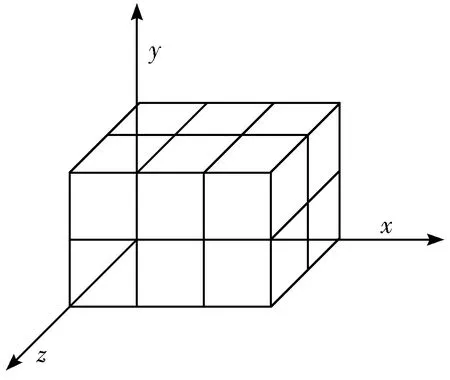
图2 复合块示意图

3.2 剩余空间最优化算法(RSO算法)

本文将三维装箱问题看作是一种带有高度约束的二维装箱问题进行求解。当纸板进行装载放置时，首先要考虑纸板在容器中如何摆放，得到一个合适的放置位置；其次，要考虑放置纸板后，所在空间如何进行分割并被划分为子空间。

当纸板被放入某一个空间中，为提高空间的利用率，需要空间分割后生成的较大子空间越大越好。在放置纸板时，观察其底面所在的平面，将分割后的子空间投影到二维平面上，分割方式有图3(a)～图3(d)这4种。由图3可知，当纸板以图3(d)放置和空间以图3(d)分割时，所产生子空间S3的底面积最大，从而所在的空间体积也最大。所以如图3(d)所示的纸板放置位置和空间分割方式最佳，这样既可以提高后面较大纸板的放置几率，也可以减少由于空间太小造成的浪费。

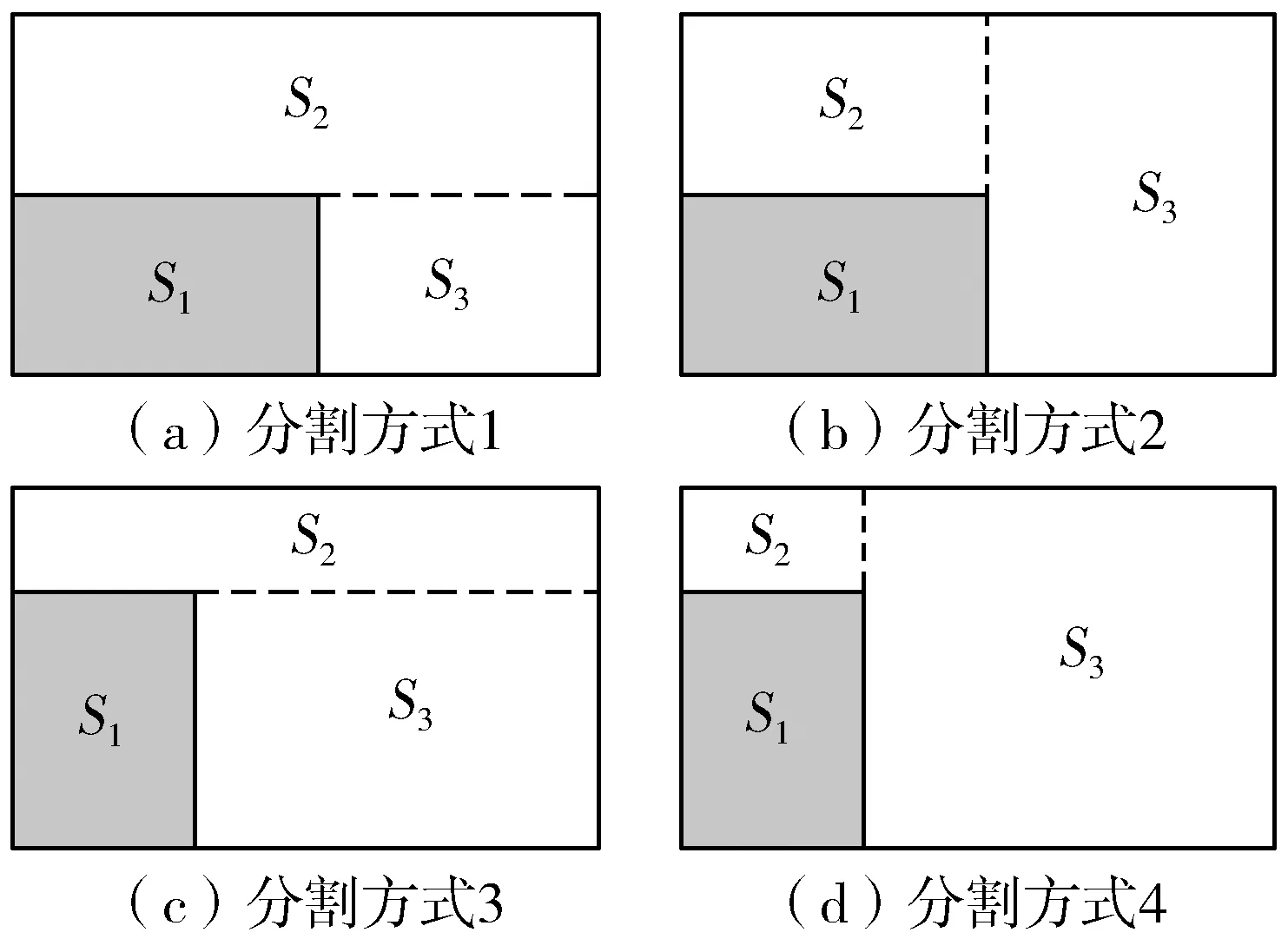
图3 纸板和空间的投影

3.2.1 分割方法

按照上文的装载布局方法，空间的分割方式采用能生成较大子空间的方式。当纸板放入容器后，其车厢的容器将会被划分为如图4所示的剩余空间，如图4(a)和图4(b)所示的3个子空间S1、S2、S3，计算比较图4(a)和图4(b)中最大子空间S3的底面积大小，选择底面积较大的分割方式。

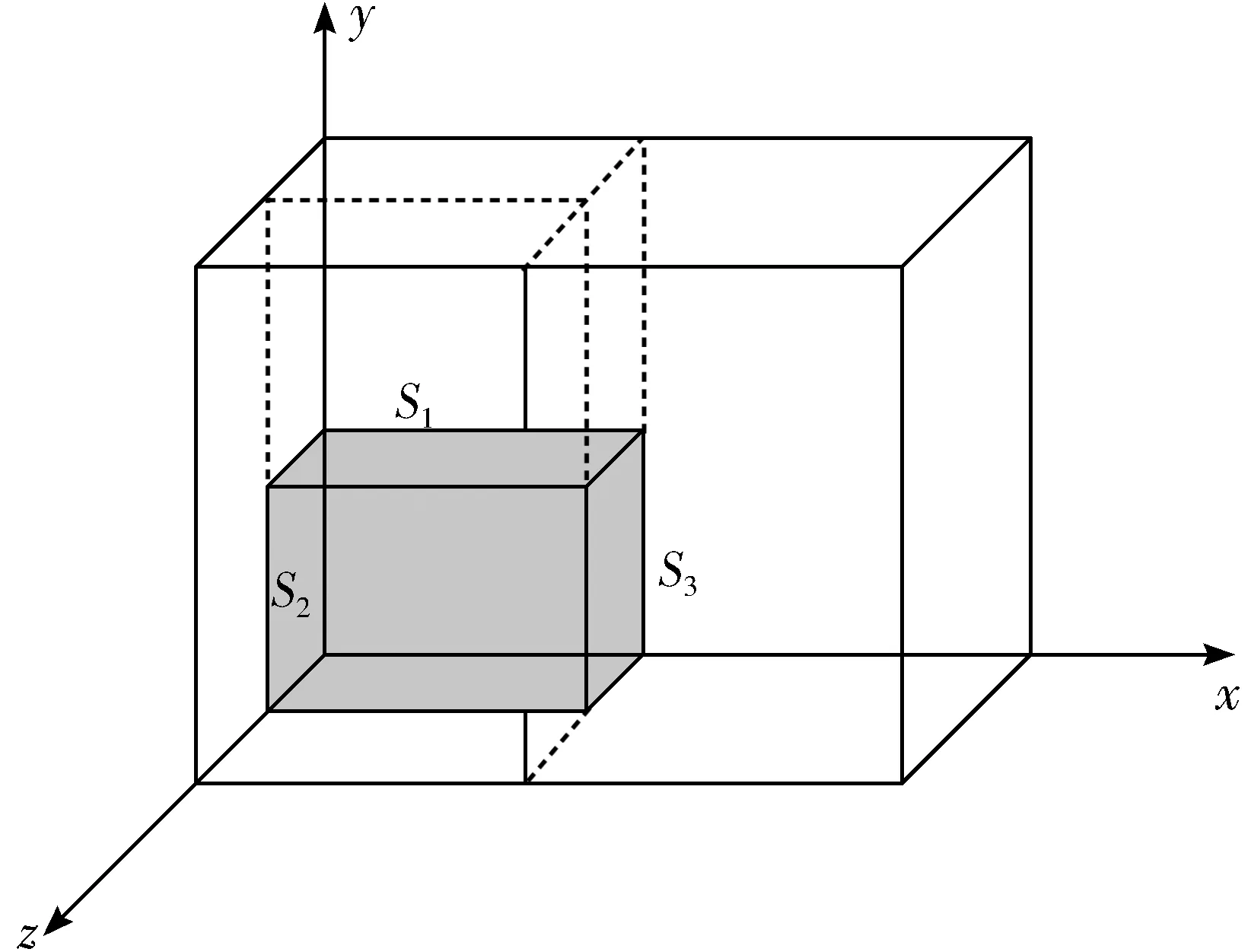
(a)分割方式1

3.2.2 放置规则

在放置纸板时，纸板的底面积与放置空间的底面积越接近，该空间则越先被进行放置，且纸板选择能生成较大子空间的放置方式。设置放置方式的评价公式为：

f(bi,Sj)=-(l(Sj)-l(bi)+α)•(w(Sj)-w(bi)+α)

(14)

其中，l(Sj)、w(Sj)分别表示放置空间的长和宽，l(bi)、w(bi)分别表示纸板放入时底面积的长和宽，α是被赋值为0.1的修正参数。放置纸板时，选择评价度高的放置方式。

根据公式(14)，如图5所示，图5(b)和图5(c)的放置是优于图5(a)的，因为纸板的底面积和空间的底面积更加接近。由于图5(c)中纸板的摆放方式能够产生较大的子空间，f(bi,Sj)的值更高，所以选为纸板的放置方式。当l(Sj)-l(bi)或者w(Sj)-w(bi)为0时，加入修正参数α能保证按评价规则仍能够选出更好的纸板放置方式。

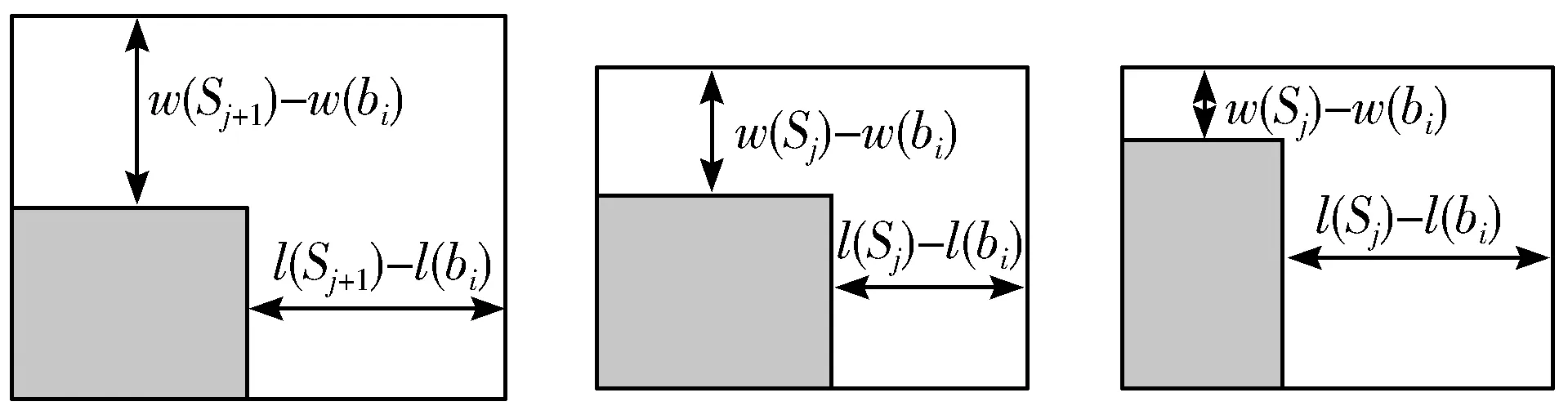
(a)规则1 (b)规则2 (c)规则3

3.2.3 空间合并

在分割空间时，会出现有剩余子空间相邻的情况，将其合并后实际上能够装下一个体积较大的纸板，但因为这2个子空间被分割开，算法将会认为无法装下。为解决这一问题，引入了相邻剩余空间合并的方法：将2个相邻且相邻边分别相等的子空间合并为一个更大的子空间，或是将2个相邻但仅有一条相邻边相等的子空间进行重新分割，判断重新分割后得到的2个空间是否相对原子空间更满足剩余空间最优化策略。若满足这一策略，则接受重新分割后得到的子空间，否则保留原子空间。

若空间S1,S2满足S1.y1==S2.y2，S1.z1==S2.z2，S1.x1+S1.l1==S2.x2，则可以进行合并，如图6(a)所示。

满足S1.y1==S2.y2,S1.x1==S2.x2,S1.z1+S1.w1==S2.z2,则可以进行合并，如图6(b)所示。

满足S1.z1==S2.z2，S1.x1+S1.l1==S2.x2，S1.y1≠S2.y2，则将空间重新分割为S1(x1+x2,y1,z1)和S2(x2,y2-y1,z2)，如图6(c)所示。

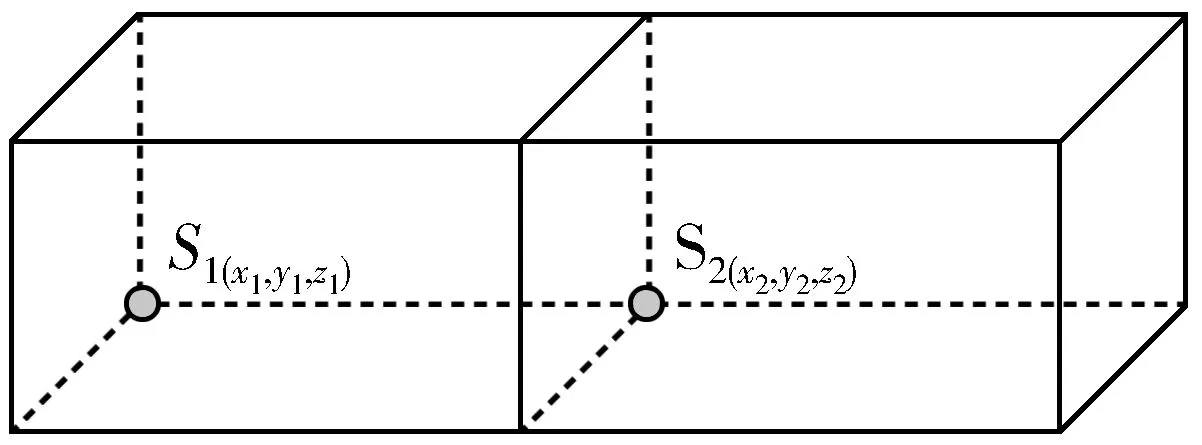
(a)合并方式1

3.3 算法流程

本文算法步骤如下：

Step1输入基本信息，包括容器的尺寸和载重量、客户的位置坐标、编号和所需的纸板编号；纸板的尺寸、数量、重量、承重级别和最大堆码数。

Step2根据3.1节设定的装箱序列确定规则，先对客户的纸板进行组合和排序，根据优先级排序，生成装箱序列。

Step3选取容器，初始化容器的空间列表，未装载之前，空间列表里只有一个空间，且数量为1。

Step4判断容器里的纸板数和纸板总数是否相等，若相等，则执行下一步。

Step5按照装箱序列，依次取出一个纸板，按照以下策略装载到容器中去。

Step5.1对纸板的尺寸、质量进行判断，是否超出容器的范围，若超出，将纸板加入Errors列表中，并返回Step4中选择下一纸板，否则执行下一步。

Step5.2计算当前纸板在所有放置状态下的评价度，形成评价度集合。

Step5.3判断容器中是否存在某个剩余空间可以放入该纸板，若能放入，则以评价度最高的状态进行放置，并将该纸板加入到该容器的装载纸板列表中；若不能放入，判断装箱序列的个数和容器个数是否相等，若相等则新建一个装箱序列，将纸板加入，否则直接将纸板加入新的纸板序列中。

Step5.4对装入纸板的该空间按照分割方法进行分割，生成新的子空间，并删除原空间，把子空间加入到空间列表中去，更新容器空间列表。

Step5.5对相邻的剩余空间进行合并或重新分割，按照空间的高度和体积大小进行排序，更新容器空间列表；跳转到Step5，继续选择下一纸板。

Step6当遍历完装箱序列中的纸板后，若容器中装载的纸板数和纸板总数不相等时，说明还有纸板未装载，取Step5.3中新生成的装箱序列，继续执行Step3，直至当所有容器里的纸板数和纸板总数相等的时，完成所有装载，并返回装箱结果。

本文算法流程如图7所示。

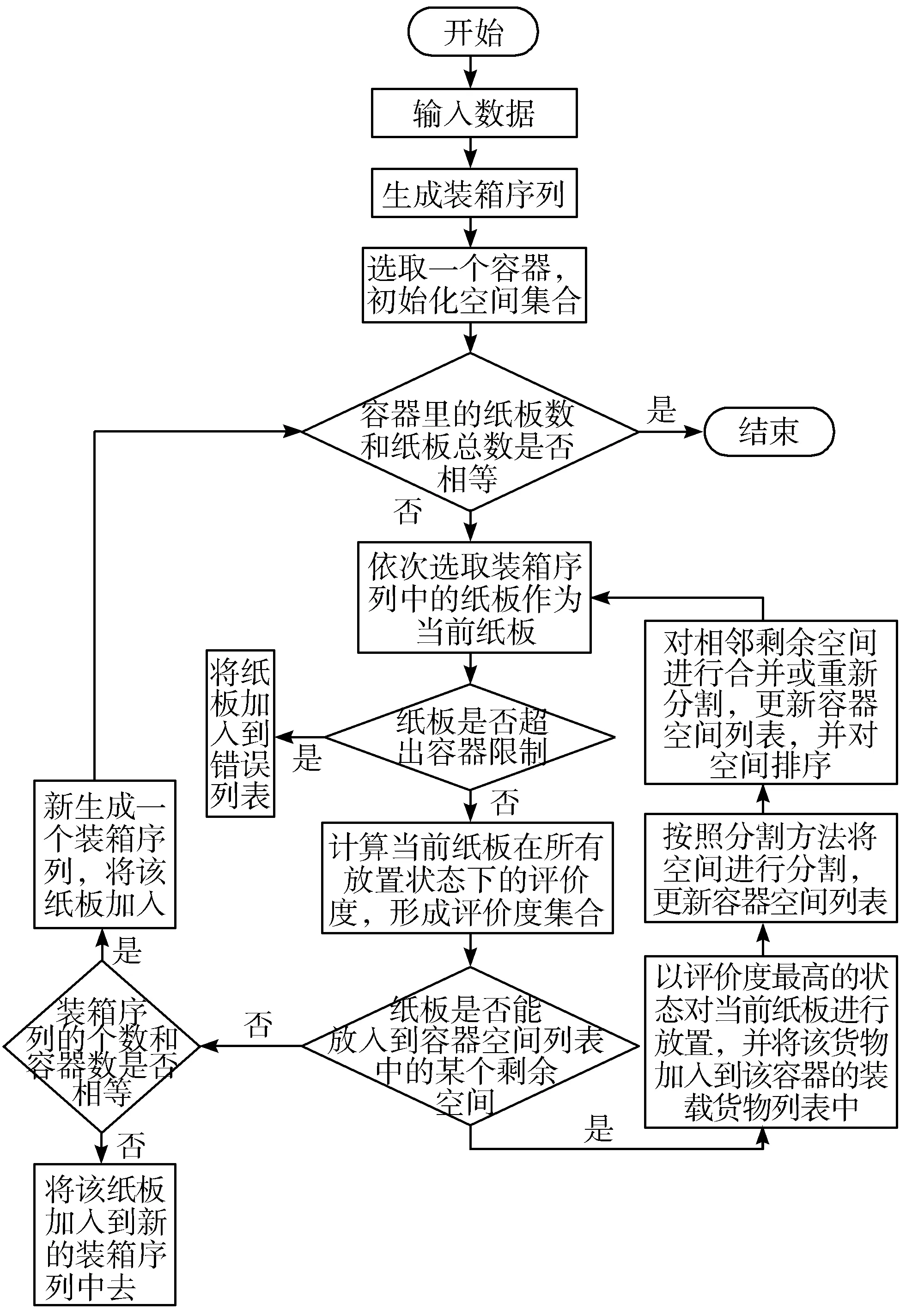
图7 算法流程

4 实验与结果

本文基于Eclipse开发平台，采用Java语言实现算法，采用Three.js三维可视化工具进行装箱结果的可视化展示。由于针对实际约束的三维装箱问题没有统一的标准数据进行对比实验，故本文先采用随机生成算例方式在验证模型与算法时，其参数设置同文献[3]一致，具体如表1所示。

表1 随机算例的设置

表1中的L、W、H表示容器的尺寸，取L=W=H，尺寸为1000 mm和2000 mm这2种，容器的最大载重量分别为1000 kg和2000 kg。对A类物品，生成种类数为5和10 的算例A5和A10，B类物品同理，每种类型各10组，物品的尺寸根据表1中的选取区间产生，共计80组算例。每种物品的数量在区间[1,⎣L/l×⎣W/w×⎣H/h]内随机产生(纸板的长、宽、高分别为l，w，h)，每个物品的重量为5 kg。设定随机算例组不考虑先进后出约束(C4)和组合装载约束(C5)，计算结果如表2所示。其中Vol，Time，BoxNum，CgNum依次表示容器的平均空间利用率、算法的平均计算时间、使用的平均容器数和每个容器装载的平均物品数。

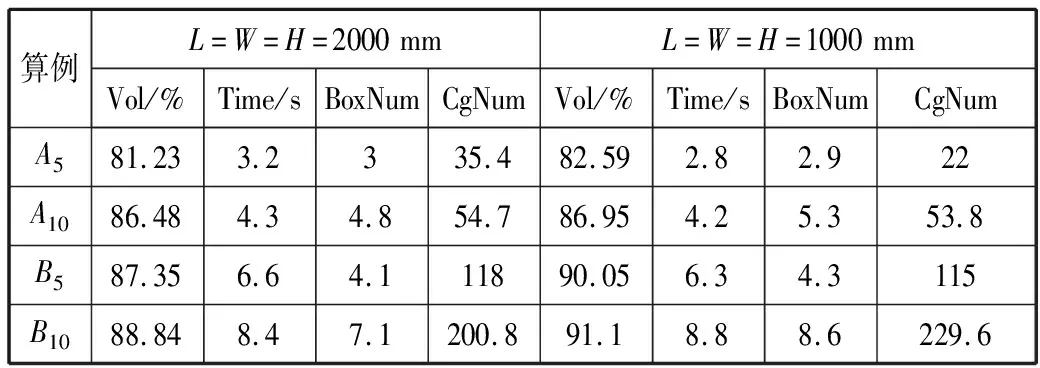
表2 计算结果

由表2可以发现：容器在装载B类物品时，其体积利用率明显高于装载A类物品，因为B类物品拥有的体积比较小，较小的空间也能够得到更好的利用，容器的空间利用率也得到了提高；容器装载种类数在较多的A10、B10时，体积利用率高于装载种类数较少的A5、B5，因为物品类型的增多能提高装载的灵活性。B类物品的装载时间明显多于A类，在种类数较多的A10、B10的装载时间多于种类数较少的A5、B5，说明装载时间受纸板总数及纸板种类数的影响，当装载体积小、数目多的纸板时，较大的问题规模导致产生较多运算时间，但由于算法运算效率高，所有算例的平均耗时均在30 s以内。

对比文献[3]算法中不考虑优先级约束，考虑承重级别约束的实验结果，由表3可以看出，整体上，本算法在容器的空间利用率要优于文献[3]算法，但由于使用的随机算例具有不确定性，所以也存在空间利用率低于文献[3]算法的情况；并且在运算效率方面，本文提出的算法更优，其计算复杂度远小于O(2n2)。

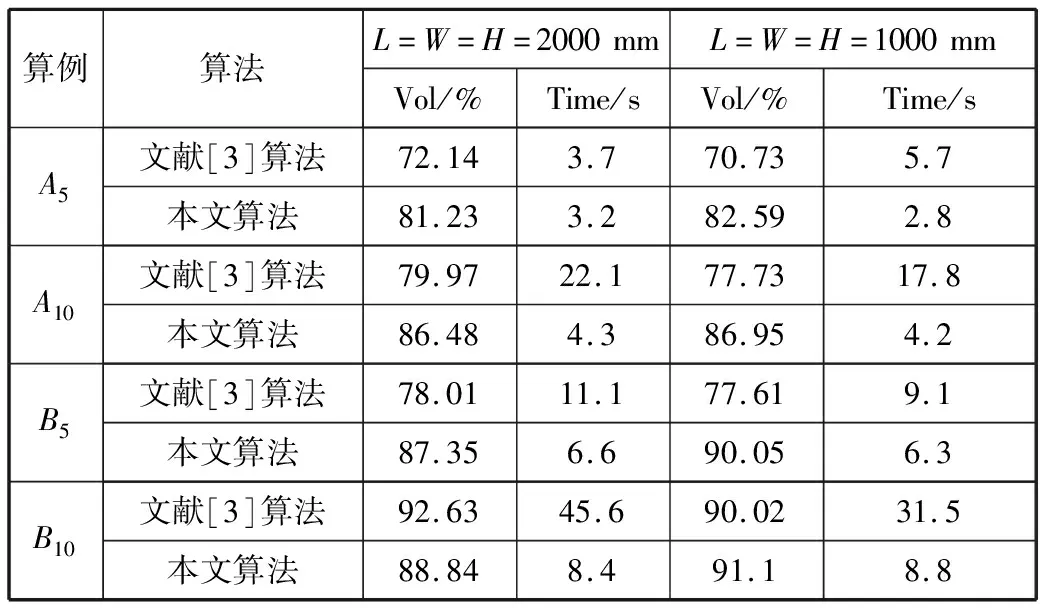
表3 算法比较结果

为进一步验证本文算法的有效性，取某公司的实际客户需求数据和纸板的基础信息数据进行分析。实际算例中，采用的容器为集装箱的国际标准尺寸5870 mm×2330 mm×2200 mm，额定载重量为1500 kg。客户数据信息如表4所示，x轴和y轴分别表示客户所在的地区与公司在x轴和y轴上的距离，可计算得到客户到公司的距离，从远到近依次为(2，1，5，3，4)；纸板数据信息如表5所示，纸板以捆计数，每一捆纸板的张数为50张，表5纸板的高为每捆纸板的高度；计算结果如表6所示，纸板的放置结果如图8所示。

表4 客户需求数据

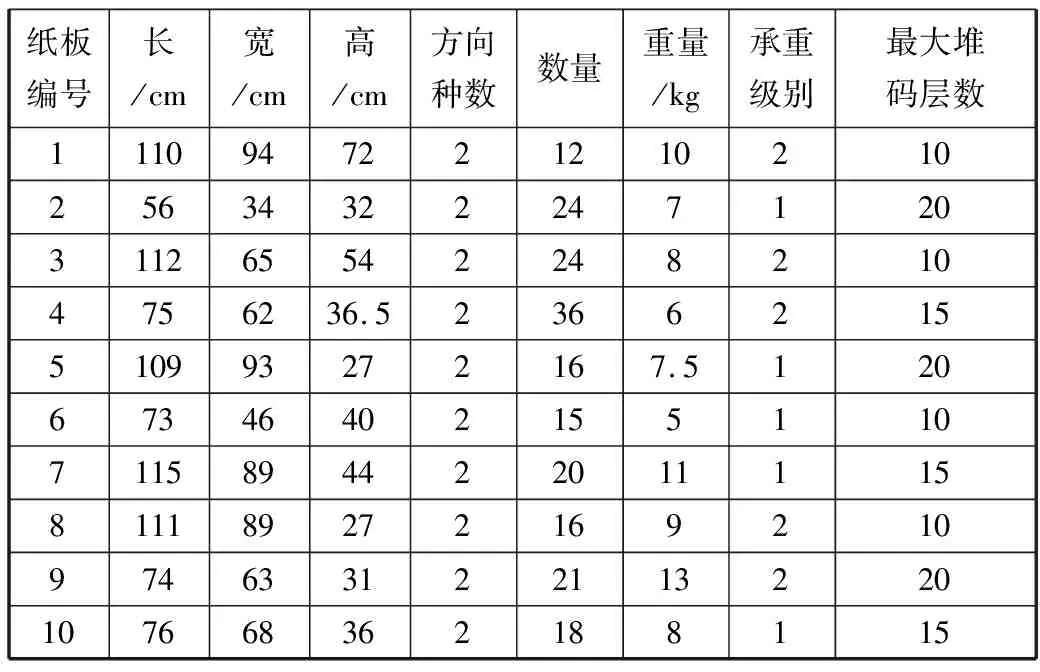
表5 纸板的基础数据信息

表6 计算结果

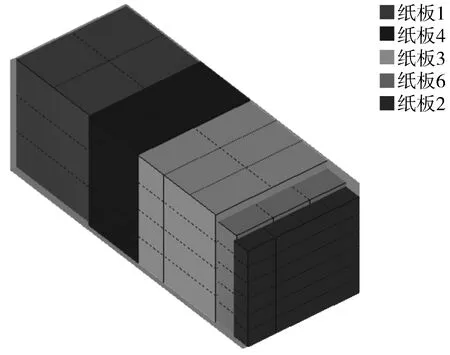
(a)容器1

由表6可以看出，241捆纸板均全部装入了2个容器中去，且容器的空间利用率均达到了91%以上；容器1装载了客户(2，1)，其纸板装载顺序为(1，4，3，6，2)，如图8(a)所示；容器2装载了客户(5，3，4)，其纸板装载顺序为(8，9，5，6，2，7，10)，如图8(b)所示。满足距离远的客户优先级相对较高，则先进行装载，距离近的客户优先级相对较少，则后进行装载；同一客户中底面积大且承重级别大的纸板优先级高，先装载，客户的所有纸板保持相邻位置装载，纸板的堆放层数均不超过最大堆放层数。

从计算结果可以看出，该算法不仅实现了多种实际约束，而且能快速进行求解，实现了容器空间利用率最高和使用数目最少的目标。

5 结束语

为满足纸板三维装箱中遇到的多种实际约束，本文建立了一个求解该装箱问题的多目标规划模型，提出了基于剩余空间最优和实际约束的算法。随机算例数据和实际数据都验证了模型的准确性和算法的有效性，而且实现了容器空间利用率最高和使用数目最少的目标，并且能在较短的时间内完成求解得到装箱方案，满足纸板生产企业的需求。未来研究中，将算法运用到实际装箱系统的开发中去，建立一个三维装箱可视化的系统以供相关企业进行应用。