SW6中法兰设计另一方法的工程应用
2021-03-23秦叔经
秦叔经
(全国化工设备设计技术中心站,上海 200040)
法兰接头的密封设计一直是压力容器设计中的重要部分。长期以来,各国压力容器设计标准提供的法兰接头设计方法是基于Waters 法的Taylor-Forge方法[1-3]。通过Waters 法可得到在压力载荷作用下法兰环中的应力分布、最大应力的数值和位置、法兰环的转角及其与应力之间的关系。然而,作为法兰接头设计的要点 - 密封设计在该方法中并未给出直接的解决方法。因此,各国规范和标准中所采用的设计方法除了限制Waters 法中计算得到的法兰环的转角之外,均利用该方法所得到的法兰环转角与应力之间为线性关系的结论,通过限制法兰环中的最大应力来间接控制法兰环的转角,从而使法兰接头满足密封性能。但在工程实践的应用中,证明按该方法设计得到的法兰连接结构并不一定能满足所需要的密封要求,这是由于该方法存在的主要缺陷:即在计算过程中,螺栓预紧力的大小与操作工况下法兰接头的密封效果无直接关联,导致设计结果不能反映实际的密封效果[4]。
欧洲标准协会(CEN)在一系列研究工作的基础上,于2001 年发布了标准EN 1591,提出了一种新的法兰接头的设计方法,该方法然后于2002 年被欧盟的压力容器设计标准EN 13445-3 采纳作为其附录G,称为“法兰和用垫片密封的法兰连接结构设计的另一规则”(“Alternative design rules for flanges and gasketed flange connections”),该方法也已被我国标准HG/T 20582—2011 采纳,为其第29 章“法兰设计的另一方法”(以下简称为“另一方法”)。以下如无说明,“标准”均指EN 13445-3 附录G 和HG/T 20582—2011。依据这些标准,我国的压力容器设计软件SW6 于2012 年将“法兰设计的另一方法”包括到其零部件设计程序中,以帮助设计人员完成以下任务:
(1)按操作工况下的密封要求以及法兰、垫片和螺栓需满足的强度要求,确定法兰接头安装时所需要的最小螺栓预紧力以及允许的最大螺栓预紧力。
(2)按法兰接头安装时所允许的最大螺栓预紧力,计算得到各工况下的螺栓力,该结果可用来确定法兰螺栓的应力幅以对其进行疲劳分析。
(3)按法兰接头安装时所允许的最大螺栓预紧力对各工况下法兰、垫片和螺栓的强度计算校核结 果。
(4)按法兰接头安装时所允许的最大螺栓预紧力计算得到的各工况下的法兰转角。
1 另一方法的推导基础和假定
1.1 确定满足密封要求的最小螺栓预紧力
利用另一方法确定法兰接头安装所需要的螺栓力可从拧紧螺栓以完成法兰接头安装开始。假想在此状况下将螺栓、垫片和法兰三者分离,那么可以知道当三者在不受力的状态下,螺栓在两个螺母之间的长度将小于一对法兰加上垫片的总厚度,它们的差值将由安装过程中将螺栓拉长同时将垫片压缩而抵消,见图1。另一方法的模型假定法兰环的厚度不发生变化,法兰环也不发生翘曲,而只发生扭转,法兰环的扭转将抵消上述的一部分沿厚度方向的差值。

图1 法兰接头预紧后螺栓长度与垫片、法兰厚度之间的差值Fig.1 Differential between length of bolt and thickness sum of gasket and flange after bolting-up of joint
为分析方便,可首先作以下假定:螺栓力、压力和其他载荷作用时法兰环不发生扭转。另外,考虑到非金属垫片在加载和卸载时应力、应变曲线将遵循不同的路径,且应力、应变之间不是线性关系,如图2 所示。为避免进行非线性分析,简化计算,标准规定,在给定垫片的条件下其弹性模量可取为:

图2 非金属垫片材料的本构关系Fig.2 Constitution relation of non-metal gasket
EG=E0+K1Q0
式中E0—— 垫片在压缩应力为0 时的压缩弹性模量;
K1—— 弹性模量随压缩应力的变化率(对于金属垫片,标准规定K1=0);
Q0—— 预紧工况下垫片的压缩应力,Q0=FG0/AGe;
FG0—— 预紧工况下的垫片反力;
AGe—— 垫片的有效面积。
在整个计算过程中,垫片本构关系曲线的斜率均取为EG,这就使得计算中将非金属垫片的材料本构关系完全按线性关系处理,大大简化了计算过程。另外,由于斜率EG总是大于斜率E0,从图2 可知,当位移一定时,材料本构关系的斜率越大,垫片反力和螺栓力就越大,故无论从保证密封性能还是法兰、垫片、螺栓三者的强度校核而言,都将得到偏保守的结果。
在此条件下,当安装完成后,差值Δ将等于螺栓的伸长量加上垫片的被压缩量,而螺栓所受的拉力与垫片所受压力的绝对值相等,其值FG与差值Δ的关系可由式(1)表示:

式中FG——垫片反力;
XB——螺栓的轴向柔度;
XG——垫片的轴向柔度;
YG——螺栓与垫片的轴向柔度之和。
由于螺栓力与垫片反力绝对值相等,均为FG,因此,也可将YG标记为对应于垫片力的柔度,即其值为作用于垫片的单位力所引起的垫片和螺栓的总变形。可将这种法兰结构预紧工况下的受力和变形以图3a 表示。

图3 法兰结构中螺栓、垫片的受力和变形Fig.3 Deformations and loaded forces of bolt and gasket in flanged joint
在操作工况下,压力载荷将施加到法兰连接结构上。由于假定法兰环不发生扭转,这时,螺栓力加大,垫片的压缩力减小,而螺栓力等于垫片反力加上压力载荷产生的轴向力。垫片反力应不小于满足密封要求的最小值,按另一方法的规定为:

式中AGe——垫片有效压紧面积;
m——垫片系数;
p——压力。
从图3b 可知,虽然操作工况下比安装工况多了压力的作用,但整个法兰结构的总变形Δ并不发生改变。其值为两部分之和:

式中FQ—— 压力产生的总轴向力;
YQ—— 压力产生法兰结构轴向变形而定义的柔度。
在图3b 中,可将操作工况下的螺栓力产生的变形分为两部分,即为平衡压力载荷的一部分螺栓力所产生的法兰结构的变形ΔQ以及螺栓变形中扣除了ΔQ后剩下的部分ΔG2。从图中还可看出,可将式(3a)中的ΔG实际是由两部分变形叠加而成,即一部分是垫片的变形ΔG1,另一部分即为上述螺栓的变形ΔG2。产生这两部分变形的力的绝对值是相同的,即等于操作工况下的垫片反力。
如果在预紧工况和(或)操作工况下还存在其他机械载荷,则在不同工况下,其他机械载荷也参与的条件下,变形差值总量Δ仍不会变化,而式(3a)将变为式(3b):

式中FR—— 除压力外其他机械载荷产生的当量轴向力;
YR—— 机械载荷产生的当量轴向力产生法兰结构轴向变形而定义的柔度。
当考虑法兰环的扭转变形时,其扭转后在垫片中心位置处垫片厚度发生了回弹,相当于在这个位置处变形差的一部分由法兰扭转造成的轴向位移抵消了。而法兰、垫片、螺栓三者沿垫片中心厚度方向的轴向变形差值总量(包括法兰偏转产生的变形)在任何工况下为定值的结论不变。法兰扭转是由于垫片反力、压力和其他机械力(力矩)通过筒体作用于法兰的扭矩而产生,扭转角应等于:

式中FΘ ——法兰环的扭转角;
F——沿法兰轴线作用的力;
h——力臂;
ZF——法兰环的转动柔度模量;
EF——法兰材料的弹性模量。
法兰转角是由垫片反力、螺栓力、压力以及其他机械载荷所形成的扭矩产生,因此,如以整体法兰为例,可以螺栓中心为原点计算法兰所受到的弯矩。由此得到的法兰转角为三部分之和:
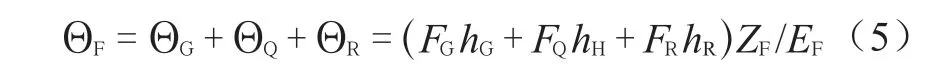
而由于法兰转角引起在垫片中心处垫片的变形量为:

考虑法兰偏转后,式(3b)中各载荷产生的轴向柔度可表示为:

式中YR—— 对应除压力外其他机械载荷的轴向柔度;
hG、hH、hR—— 对应垫片反力、压力、其他机械载荷的力臂。
一般情况下,力臂hH大于hG,因此,即使考虑一些其他因素后,同为单位力的压力载荷合力产生的扭矩仍将大于垫片反力产生的扭矩。当再计入操作工况下螺栓与法兰、垫片的温度变形差ΔU,根据在任何工况下轴向变形差Δ值不变的结论,即可得到法兰连接结构安装时为各操作工况下满足密封要求的螺栓最小预紧力为:

式中FGI,min=QI,minAGe=mIpIAGe—— 各操作工况下满足密封要求的最小垫片反力;
mI——垫片系数,与泄漏率有关。在预紧工况下所需的最小垫片反力FG0,req除了应不小于式(8)确定的FGΔ之外,还应不小于垫片在安装阶段所需最小压紧力Q0,minAGe。即

标准提供的所有垫片参数,包括mI和Q0,min,均来源于实验测量、工程经验和估算,虽然标准对于各种垫片给出了这两个参数值,但并不要求对这些参数必须按标准取值。因此,对于Q0,min,如果各操作工况下垫片反力QI,min的值均基于泄漏紧密度准则确定,则可取Q0,min= 0[3,5]。但标准并未明确在什么条件下可认为QI,min的确定是基于泄漏紧密度准则。因此,在工程应用时可以认为,当在计算中考虑了所有可能发生的工况,并对这些工况都规定了合适的垫片系数mI·,则应满足了标准所要求的基于泄漏率准则确定QI,min的条件。
在预紧工况下,为满足密封要求需要的最小螺栓力FB0,req等于垫片反力FG0,req,而不同的法兰螺栓的上紧方法和程序将使得各螺栓的受力有所不同。因此,标准引入了分散系数εn+、εn-以考虑法兰安装过程中实际螺栓力可能的增大和减小,据此定义的名义预紧螺栓力应为:

该值即应为标注于装配图上所要求的法兰螺栓预紧力。同样考虑螺栓上紧过程中的分散性,当按图纸所标注的螺栓力进行上紧时,螺栓力可能达到的最大值估计为:

1.2 确定允许的最大螺栓预紧力
法兰安装过程中,螺栓预紧力越大对法兰接头的密封性能越有利,但在其他条件都不变的情况下,在垫片、螺栓和法兰中的应力也越大。因此,需要通过对垫片、螺栓和法兰的强度校核来确定安装工况下允许的最大螺栓预紧力。在校核法兰接头中各零件的强度时,另一方法都采用载荷比来表述,在任何工况下,各零件的载荷比φI≤ 1.0。
标准规定,按另一方法进行法兰连接结构中各零件的强度校核时,对于预紧工况,应采用最大螺栓力FB0,max为基准来得到垫片反力FG0,然后对螺栓和垫片进行强度校核。而对于各操作工况,按以下公式确定预紧工况下的垫片反力[2-3,5]:

式中NR——设备设计寿命内法兰接头的拆装次数。
式(12)表示的螺栓设计载荷FG0,d按以下方法推导得到[6]:
在法兰安装阶段,按另一方法可估计实际螺栓力FB0,act的数值范围为(FB0,min,FB0,max),如果法兰结构需多次拆装,拆装次数为NR,则应考虑控制螺栓的渐进塑性变形:

对于一般的塑性金属材料,当螺栓力为FB0,max使得应力水平达到许用应力时,其εmax约为0.001 ~ 0.002[6],将累积应变值控制在0.01 是合理的,故可取C=10。另外,为了保证螺栓不发生屈服,可取安全系数1.5,即螺栓设计载荷FB0,d=FB0,act/1.5,于是,式(13)变为:

预紧工况下的垫片反力FG0,d应为(FB0,d-FR0),即为式(12)右端的第二项。式(12)中的FGΔ是满足各工况下密封要求的最小垫片预紧力,按式(8)计算得到。但当螺栓预紧力大于密封所需要的最小预紧力时,垫片预紧力相应地也将大于FGΔ,这时,各操作工况下的垫片反力和螺栓力都将增大。因此,在确定螺栓预紧力范围时,SW6 将按照密封所需要的最小螺栓预紧力与垫片预紧力之间的关系式(9),由每步长确定的螺栓力FB0,req来推得式(12)中的FGΔ:

实际计算表明,按式(12)计算设计螺栓预紧力FG0,d时,绝大部分情况下式中的第一项FGΔ将起控制作用。
相应地,各操作工况下的垫片反力和螺栓力为:

在式(12)的推导过程中,将实际螺栓力除以安全系数后作为螺栓设计载荷,降低了螺栓、垫片、法兰强度校核的载荷值,从设计理念上是不合适的。因此,在标准的说明中也承认操作工况下没有按可能达到的最大螺栓力对螺栓进行强度校核[2]。但标准认为,高于平均螺栓力的那部分载荷产生的是二次应力,一方面它们具有自限性,另一方面,当个别螺栓达到屈服后,螺栓力将在其周边螺栓或全部螺栓中重新分配,使得螺栓力的分配更趋于平均,而不至于使得个别螺栓的强度失效。
(1)垫片强度校核
标准所给出的垫片系数中包括了垫片的许用压缩应力Qmax[3-4,6],垫片的载荷比为:

式中FGI——工况I 的垫片反力;
AGt——垫片理论面积;
cG—— 修正系数,cG= 1+bG(/20eG),其中,bG为垫片宽度,eG为垫片厚度。
(2)螺栓强度校核
计算螺栓的载荷比时需考虑的因素包括:
a)螺栓的载荷比为:

式中,fBI为螺栓材料的许用应力。摩擦系数μ按螺栓上紧时螺母与螺柱间是否有润滑来确定,标准对于各情况给出了一些摩擦系数的取值范围,可进行参考。
b)系数C按以下取值:当螺栓材料的断后伸长率不小于10%时,可以认为该材料允许存在小部分屈服,可取系数C= 1.0;而当螺栓材料的断后伸长率小于10%时,应认为该材料不允许存在小部分屈服,应取系数C= 1.333。当法兰安装完成后,螺栓不再受到扭矩作用时,可取系数C= 0(如使用液压张紧器来上紧螺栓的情况)。
(3)法兰强度校核
在另一方法中,法兰的强度校核理念与Taylor-Forge 方法不同。另一方法假定法兰能够承受的最大扭矩为使得整个法兰环截面中的切向应力都达到材料许用应力的那个扭矩,即允许法兰环截面达到全屈服[7]。对于整体法兰或其他直接与各种壳体相连的法兰,法兰截面包括法兰环和与之相连的锥颈或一部份壳体,它们将作为一体进行弯曲强度校核。对于松式法兰,法兰环和与之相连的翻边或凸缘需分别进行强度校核。
整体法兰、松式法兰的翻边或凸缘的载荷比为:

松式法兰的载荷比为:

式中,WF和WL相当于抗弯模量与应力许用值的乘积。对于松式法兰的翻边或凸缘,φmax取1.0;对于外径与内径的比值χ不大于2.0 的整体法兰或松式法兰,φmax取1.0;而对于外径与内径的比值χ大于2.0 的整体法兰或松式法兰,φmax可按下式计算而得到更精确的取值:
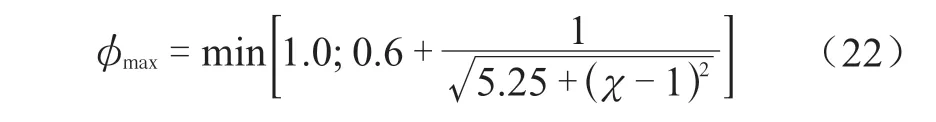
为了得到允许的最大螺栓预紧力,可从满足密封要求的最小螺栓预紧力开始,以一定的步长,渐进地增大螺栓预紧力FB0,nom,以此确定FB0,max=FB0,nom(1+εn+)以及FG0,d,然后分别校核螺栓、垫片和法兰的强度,直到这三个零件中有一个强度不合格。这时,可取最后那个校核合格的螺栓预紧力作为螺栓预紧力范围的上限。
另一方法还提供了计算法兰转角的方法:

整体法兰的转角按式(23)计算,松式法兰的转角按式(24)计算。但标准未规定法兰转角的限制值。
2 计算实例
如前所述,SW6 的主要计算目标一是针对给定载荷条件的法兰连接结构(包括法兰结构形式和尺寸),确定该法兰连接结构安装时的螺栓预紧力范围;主要计算目标二是确定各工况下的螺栓力。对于第二个目标,由于没有要求SW6 的用户在螺栓预紧力允许范围内指定某一特定值,因此,软件将按螺栓预紧力允许范围的上限给出各工况下的螺栓力。通过式(16)和式(17)确定工况I 的螺栓力FBI时,都将基于式(12)得到的设计垫片反力FG0,d,且FBI与FG0,d成线性关系,故各工况下螺栓力的差值将不会因螺栓预紧力的不同而变化。
另一方法计算模型的基础与Waters 法不同,该模型是基于一对法兰或法兰与螺栓连接端盖的连接结构进行计算。本文的目的是通过以下算例计算和检验标准法兰所需要的螺栓预紧力以及演示多种条件下预紧螺栓力的变化情况,因此,文中所有算例均按一对同样结构形式的法兰进行计算。算例中除了对给出的温度、压力组合工况计算之外,均同时考虑并计算预紧工况。
算例1:选自管法兰标准HG/T 20592—2009,PN 25,DN 100,带颈对焊法兰,材料为锻件16Mn;螺栓、垫片类型组合:组合a:螺栓材料40Cr,垫片为无金属内嵌的膨胀石墨软垫片;组合b:螺栓材料35CrMoA,垫片为石墨缠绕垫;计算工况:a)t= 20℃,p= 2.5 MPa;b)t= 300℃,p= 2.09 MPa。计算结果见表1。

表1 算例1 计算结果Table 1 Calculation result of example 1
算例2:本算例包括两对法兰的计算,一对选自管法兰标准,另一对选自容器法兰标准,目的是将该两对压力等级基本相同的法兰的计算结果进行比较。这两对法兰结构类型相同,都为高颈法兰,结构尺寸按标准确定。这两对法兰采用同样的垫片类型和材料,法兰材料为锻件16Mn。螺栓、垫片类组合:螺栓材料35CrMoA,垫片为外包石墨的不锈钢槽形垫片。按同样的计算工况进行计算:a)t= 20 ℃,p= 6.3 MPa;b)t= 300 ℃,p= 5.27 MPa。螺栓上紧方式采用扭矩扳手,螺栓强度校核用系数取1.0(螺栓材料有足够韧性)。计算结果见表2。

表2 算例2 计算结果Table 2 Calculation resultof example 2
将本例中的容器法兰按GB/T 150 的法兰设计方法(Taylor-Forge 法)进行校核,经对照两个方法的计算结果,发现Waters 法计算得到的垫片有效面积约为另一方法计算结果的0.89 倍,故将Taylor-Forge法所用垫片系数m和y的取值为另一方法所取值的1.12 倍,计算结果为螺栓强度校核合格。两个方法计算结果的不同原因主要为以下三个方面:
(1)Taylor-Forge 法是按预紧工况和操作工况对螺栓力分别进行计算,两个工况下得到的螺栓力是没有关系的,仅取大值进行校核即可。而在另一方法中,为保证操作工况下的垫片有满足密封要求的压缩应力,是通过螺栓、垫片和法兰的变形协调来计算预紧工况下螺栓所需要的预紧力。在这个过程中,需计及法兰的转角在变形协调中的影响,而对于同样大小两个力–垫片反力和压力,后者的力臂要大于前者,即按式(7a)和式(7b)计算得到的柔度,后者将大于前者,相当于在式(8)计算时,将力FGI放大了(YQ/YG)倍;
(2)对于预紧工况下的强度校核,另一方法规定采用最大螺栓预紧力进行计算,即需要考虑分散系数εn-和εn+,该最大螺栓预紧力将是满足密封要求的名义螺栓预紧力的(1+εn+)倍;

从以上对本例中容器法兰计算结果的分析可知,从满足密封要求的角度看,按Taylor-Forge 法进行法兰设计的结果可能是不安全的。
算例3:本算例选自管法兰标准HG/T 20592—2009,PN 160,DN 300,带颈对焊法兰,材料为锻件12Cr2Mo1。螺栓、垫片类组合:螺栓材料35CrMoA,垫片为不锈钢八角垫,Class 900。计算工况:a)t=350 ℃,p= 15 MPa。计算结果见表3。

表3 算例3 计算结果Table 3 Calculation result of example 3
3 讨论
在使用SW6 对法兰进行设计计算时,有一些输入参数的值标准允许由设计人员来确定。当这些参数以不同的值输入,自然会得到不同的计算结果。因此,有必要对如何确定这些参数的值进行一些讨论。另外,对于软件按另一方法计算后得到的法兰转角,应正确理解其对法兰接头的影响,从而在设计中合理的进行使用。
(1)垫片系数mI和Q0,min
这两个系数mI和Q0,min与Waters 法中的m、y相对应,但由于在计算中所规定的垫片有效宽度以及垫片有效直径不同,故另一方法中这两个系数的取值与Waters 法中的取值也不同。在另一方法中,操作工况下满足密封要求的最小垫片压缩应力为:

即需要的最小压缩应力QI与压力腔中的压力p成正比。标准中所给出的垫片系数mI的大部分数值是在以下条件下得到的结果[3]:
常温下p= 40 bar 的氮气,实验用垫片的内、外径分别为50 mm、90 mm,泄漏率为1 mL/min(折合到室温和标准压力条件下)。
在该测试条件下对应的泄漏率可换算成为L= 0.086 4 mg/ (s·m),可知系数mI在一定条件下与泄漏率可以是挂钩的,因此,当确定了实际需要达到的泄漏率,就可按折算后的mI采用另一方法进行法兰接头的设计。使用mI的意义在于当压力为p时,在操作工况下,只要垫片压缩应力达到mI|p|,在实际介质与试验介质的泄漏能力相当的条件下,则应得到与测试条件基本相同的泄漏率。然而,按EN 1591-2:2008[8]所发表的数据,在大部分情况下,QS(min)与压力p之比值都大于[3]中的mI。考虑到EN 1591-2 中QS(min)与泄漏率有关,可以将EN 1591-2 中对应泄漏率为L0.1的QS(min)除以4.0 MPa后与[4]中发表的mI进行对比。究其原因,应该是与两个标准在数据测试时所用的介质有关,即在EN 1591-2 中是以氦气为介质,其他测试条件与[3]相同。因此,当按另一方法进行法兰设计时,如希望得到更理想的密封效果,可参照文献 [8]中的QS(min)计算得到mI(mI=QS(min)/|p|),然后代入另一方法中进行计算。
另外,按文献 [4]中附录GA 给出的有关法兰接头紧密度与垫片反力的关系数据,当操作工况下压力升上去后,为达到预定密封要求的最小垫片压缩应力GS(min)同预紧工况下所施加的实际垫片压缩应力QA有关,QA越大,所需要的QS(min)越小,在附录GA中所给出的曲线中这个趋势非常明显。但从文献 [8]所发布的非金属垫片、缠绕垫片、金属包垫片以及其他组合材料垫片的性能数据看,这个趋势并不明显,所给出的大部分垫片的数据甚至看不出有这个结论。因此,在计算中只按泄漏率确定mI,而不考虑实际预紧状态的垫片反力对其的影响应该是合理的和可接受的。但从密封原理来看,在螺栓、垫片和法兰的强度都足够的条件下,螺栓预紧力越大,密封效果应越 好。
Q0,min是法兰接头预紧工况要求的最小垫片压缩应力,施加Q0,min的作用是尽可能将介质在压力差作用下流动的微细管道关闭,或进一步缩小微细管道的流通截面积,从而增加流动阻力。然而,在文献 [3]中没有明确说明Q0,min的测量方法,从而无法得到其与系数mi的关系。文献[11]中给出的Q(min)意义与文献 [4]中Q0,min的意义相同,按文献[9]中规定的方法可测得各种垫片的Q(min)。按该参数的测定方法,该值总是小于QA(QA是为在操作工况下垫片压缩应力达到QS(min)而在预紧时所需要达到的实际垫片压缩应力),故在计算中可将QA作为Q0,min参考值输入而在式(9)中使用。计算得到的预紧工况下所需垫片压缩应力应不小于文献 [8]提供的与QS(min)所对应的QA。从一些算例可知,在大部分情况下,Q0,min按0 输入并不影响最终的计算结果(该结论可在本文三个算例中都得到验证)。
随着近些年法兰设计另一方法的发展,该方法已可与泄漏率真实地结合起来了。事实上,可以认为本文方法中所使用的垫片参数Q0,min相当于EN 1591-1 :2009[10]中的Qmin[L],参数m与压力p之乘积相当于文献[10]中的QSmin[L]。文献 [10]中方法所使用的QSmin[L]意指泄漏率为L基础上在操作工况下所需的垫片最小压缩应力。按照文献 [9]所规定的测试条件和方法可得到的该值,而该参数又与对于特定垫片试验中预紧工况下所施加的实际垫片压缩应力相关联[9]。因此,本文所述的法兰设计另一方法相比于现行标准中的法兰设计方法前进了一大步,至少在设计中通过计算可以初步确定所选用的法兰结构和垫片在预紧阶段为了达到密封要求所需要的螺栓预紧力的大致范围,同时可以通过计算得到的各工况下螺栓力确定螺栓的应力变化范围。
(2)法兰环转角对密封性能的影响
法兰环的转角将对法兰接头的密封性能有较大影响,虽然在另一方法关于法兰、垫片、螺栓的变形协调计算中考虑了法兰环转角的影响,但在所有计算中假定垫片在有效宽度范围内受到的是均布压紧力,显然这个假定与实际状况不符。当法兰发生偏转后,垫片外侧所受压紧力将大于内侧,也即垫片外侧所受压紧力可能大于垫片强度校核计算中所用的值。当垫片外侧的实际压缩应力大于能够承受的最大值时,该部分垫片即会被压垮,即丧失回弹能力而使得法兰接头的密封失效。因此,在实际工程设计中应该对法兰环的转角加以限制。
为了按转角的限制值确定螺栓预紧力的上限,一方面,针对各类法兰、垫片组合的密封性能可参照工程经验;另一方面,当缺乏工程使用经验时,可参考ASME VIII-1 中关于法兰刚度校核中的法兰转角限制,即对于整体法兰限制其转角不大于0.3 度,而对于松式法兰限制其转角不大于0.2 度。SW6 默认采用以上法兰转角限制值,如有试验数据或工程使用经验,可通过软件安装目录“..dataFlangeAR”下的文件“anglelimit.txt”对转角限制值进行修改。
(3)法兰环转角对螺栓应力的影响
在标准提供的另一方法中,法兰螺栓是按仅受拉伸的力学模型进行计算[3,5,10],SW6 的有关程序也是照此执行。然而,实际上法兰环发生扭转以后势必导致法兰螺栓产生弯曲,该弯曲应力将和拉应力叠加而对螺栓的强度有所影响。对于一对结构相同的法兰,当法兰环转角为ΘF,则螺栓中的弯矩M和最大弯曲应力σmax可分别按如下进行计算:
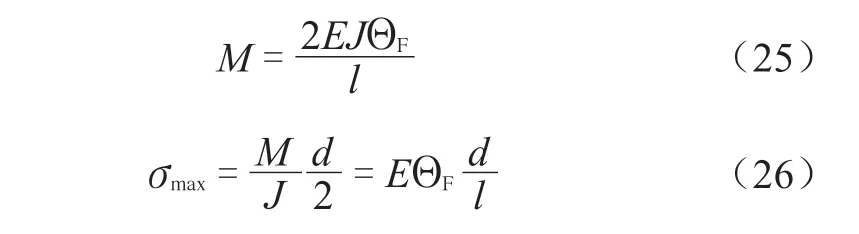
由于弯曲应力完全是位移载荷产生,故对于不需考虑疲劳失效的情况,虽然在另一方法中未对螺栓中的总应力(拉应力+弯曲应力)进行校核,但由于确定许用应力时所使用的安全系数、位移载荷产生的二次应力具有自限性以及一定程度上对法兰环转角进行了限制等三个因素,在法兰螺栓拉伸强度足够的条件下,该弯曲应力的存在并不会造成螺栓的失效。
如需进行疲劳分析,则从式(26)可知,对于同样大小的法兰转角,螺栓的最大弯曲应力将与其直径成正比。故这时应在保持螺栓总截面积不减小的前提下选择较小螺栓直径和较多的螺栓个数,以尽可能减小弯曲应力,从而减小总应力。由于SW6 的计算结果中未给出法兰螺栓的弯曲应力,故设计者应自行按式(25)、(26)计算后得到总应力,再根据不同工况确定螺栓的最大应力幅。
4 结论
当规定了操作工况下法兰密封面与垫片之间所需要的最小压紧力后,可利用SW6 按文献[3, 5]所给出的法兰设计另一方法计算得到法兰接头安装时的螺栓预紧力范围。当在工程图纸上需要标注法兰接头的螺栓预紧力时,一般应按SW6 给出的螺栓预紧力范围的上限值标注以得到较好的密封效果。同时,SW6 除按另一方法对法兰、垫片、螺栓进行强度校核之外,计算结果中还给出了各工况下的螺栓力以及法兰转角,这些数据将可用于法兰螺栓的疲劳分 析。
在标准EN 13555—2004 中规定了垫片系数的测定方法和条件,使得另一方法中使用的垫片系数mI可与泄漏率直接挂钩,即在使用SW6 进行螺栓连接法兰接头的设计时,即可直接利用文献 [3]中提供的垫片系数Q0,min和mI,也可按文献 [8-9]确定QA和QSmin[L],将QSmin[L]折算到mI,然后进行计算。而且,当工程建设中对于特定介质的泄漏率有明确规定时,也可按该标准中的方法测得垫片系数,然后利用另一方法进行法兰接头的精准设计以满足设备的密封要 求。
