塔式容器地脚螺栓拧紧力矩计算及应用

仇放

（中国石油工程建设有限公司，北京 100120）

塔式容器安装中最常见的就是用地脚螺栓连接和固定设备，通过拧紧力矩施加预紧力从而防止设备受载荷后出现分离、扭转或相对滑移，以此增加连接的可靠性和紧密性。实践表明，地脚螺栓加载的拧紧力矩过大会导致螺栓变形甚至拧断，拧紧力矩过小则起不到固定设备的作用，对设备相连管线和装置平稳运行产生隐患[1]。

目前，对地脚螺栓的拧紧扭矩值的确定主要采用以下三种方法：

（1）紧密拧紧。即AISC 钢结构安装指南中地脚螺栓可采用紧密拧紧（Snug Tight）[2]，是指连接中的所有层都已通过接头中的螺栓拉紧并牢固接触，并且接头中的所有螺栓均已充分拧紧，在不用扳手的情况下无法卸下螺栓。此方法未规定拧紧力矩值，直接受有经验的操作工人影响，最终效果偏差大。

（2）查表取值。即地脚螺栓拧紧力矩值的确定可以根据SH/T 3538—2017《机器设备安装工程施工及验收通用规范》[3]、HG/T 20203—2017《化工机器安装工程施工及验收规范（通用规定）》[4]和API RP 686—2009《机械装置和装置设计的推荐实施规程》[5]进行选取，见表1。此方法受地脚螺栓材质、直径限制。

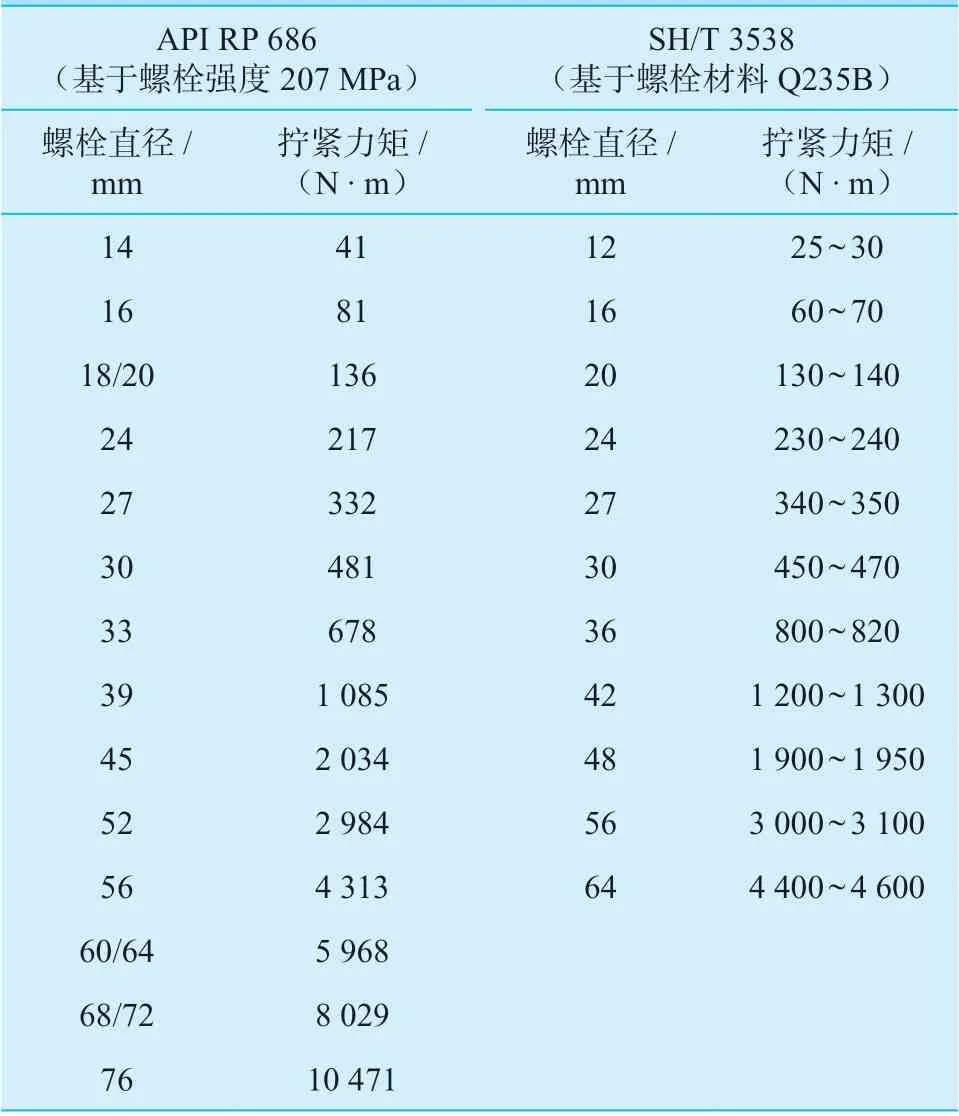
表1 拧紧力矩查表法Table 1 Tightening torque in look-up table method

（3）实验法。运用校准的力矩扳手对螺栓进行拧紧测试，记录每次螺栓失效的最大力矩，计算平均最大失效力矩，取0.6 倍系数后得到螺栓拧紧力矩[6]。此方法准确度高，但是现场一般不具备做实验的条件，实用性不高。

实际工程中，大型设备的螺栓直径较大，螺栓材料多样，需要通过计算获得拧紧力矩。本文通过地脚螺栓的受力分析计算预紧力，进而得出地脚螺栓拧紧力矩的计算方法，并与俄罗斯标准SNIP 2.09.03 MDC 31-4.2000 地脚螺栓拧紧力矩计算方法进行对比分析，从而得出适用于实际工程计算拧紧力矩的方 法。

1 拧紧力矩计算方法

1.1 方法（1）基于受力分析的地脚螺栓拧紧力矩

螺栓在工作状态下既受预紧力F0又受轴向载荷F的作用。螺栓在预紧力F0作用下伸长λL，被连接件被压缩λF，见图1a。螺栓工作后，在工作拉力F的作用下继续伸长Δλ，螺栓总伸长量λL+Δλ，螺栓受到的总拉力为F2；被连接件相应的压缩量降低Δλ，总压缩量缩小为λF-Δλ，其受力为F1，即残余预紧力，见图1b。

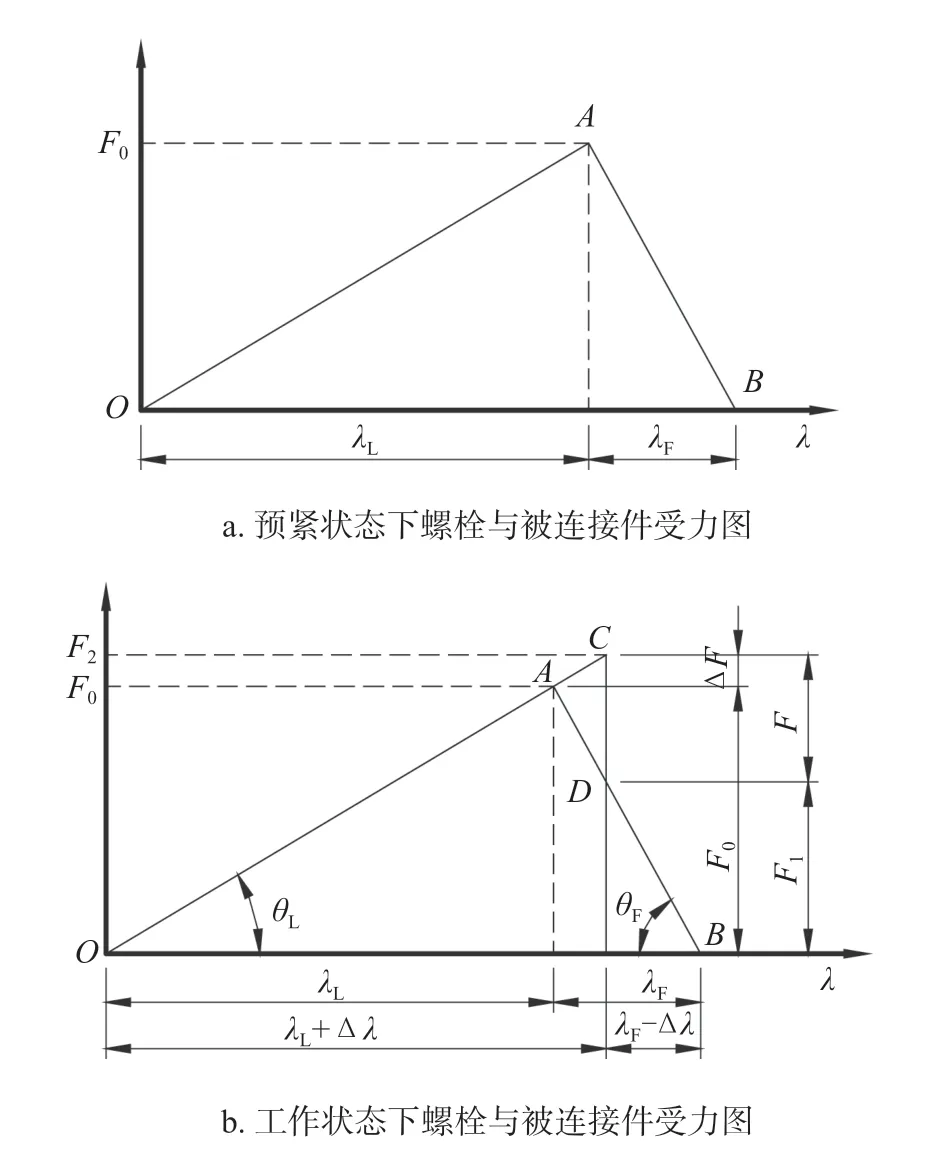
图1 螺栓与被连接件受力分析图Fig.1 Stress analysis chart for bolts and connected parts

根据几何关系可以推导出：

式中，CL= tanθL为螺栓刚度，CF= tanθF为被连接件刚度，均为定值。

联立公式（1）、（2），可以得出螺栓预紧力F0为：

表2 预紧螺栓连接所需残余预紧力F1 及螺栓连接的相对刚度系数Table 2 Residual preload F1 required for the pre-tightening bolt connection and relative stiffness factor of the bolt connection

从机械设计手册可知，螺栓拧紧力矩计算公式如下[7]：

式中d——螺纹公称直径，mm；

F0——预紧力，N；

k——拧紧力矩系数，见表3。

1.2 方法（2）基于俄罗斯标准SNIP 2.09.03 MDC 31-4.2000的地脚螺栓拧紧力矩

在静载荷情况下螺栓预紧力F0= 0.75P，在动态载荷情况下F0= 1.1P。塔式设备主要采用裙座的支撑方式，应根据以下公式确定最大螺栓载荷下每一个螺栓的计算载荷P[8]。

式中N——设备轴向应力，N；

n——螺栓数量；

M——设备所受弯矩，N·m；

y1——设备轴线到最远螺栓的距离，m；

yi——每个螺栓到设备轴线的距离， m，见图2。

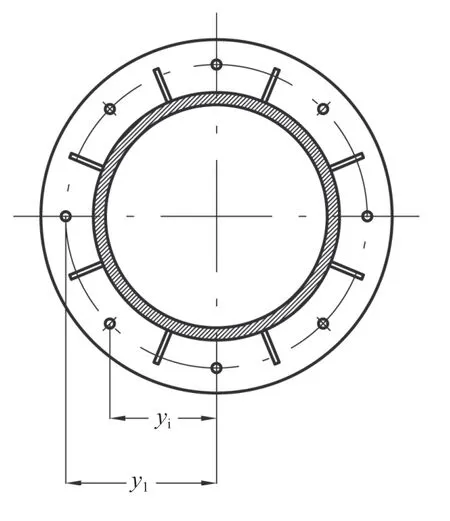
图2 螺栓分布示意Fig.2 Sketch diagram of bolt distribution

考虑风载和地震载荷的影响，地脚螺栓会受到剪切力的作用，因此修正的预紧力 需要用以下公式进行修正。

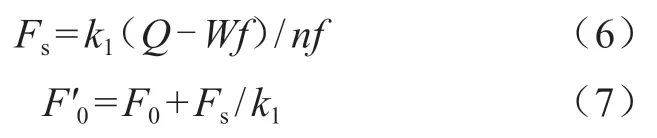
式中Q——螺栓所受剪切力，N；

W——设备自重，kg；

k1—— 拧紧稳定性系数，动载荷下取1.9，静载荷下取1.3；

f——摩擦系数，取0.25。

地脚螺栓拧紧力矩TR，按以下公式计算：

系数ζ需考虑螺纹的几何尺寸，螺母端部和螺纹间的摩擦，按表4 进行选取。

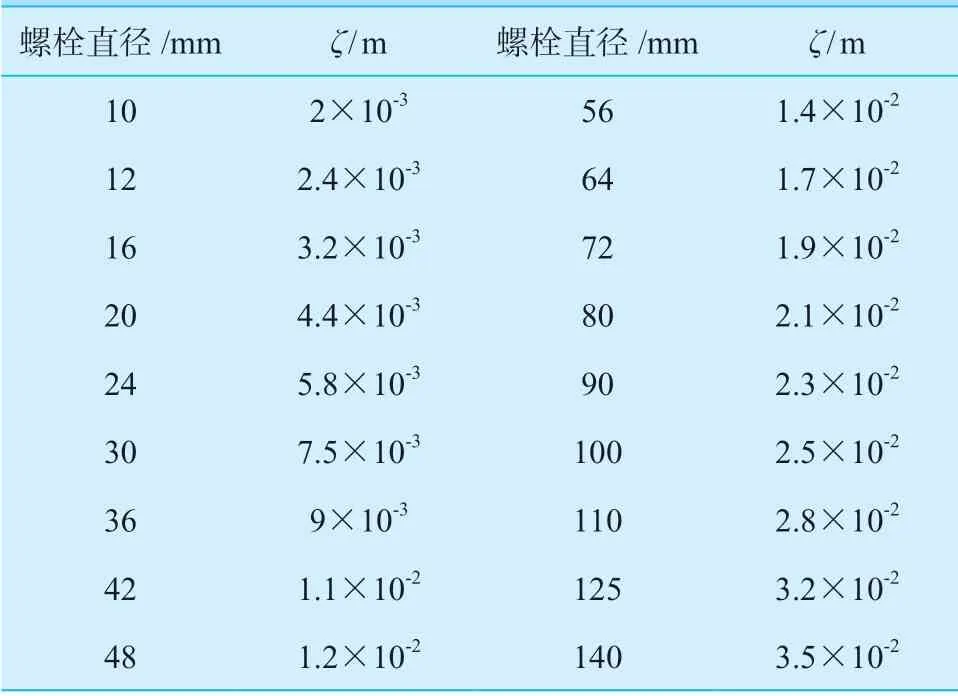
表4 拧紧力矩系数ζTable 4 Tightening torque factor ζ

2 实际算例

以俄罗斯某天然气处理厂塔式设备为例，设备资料见表5。

表5 设备汇总Table 5 Summary of equipment

2.1 拧紧力矩计算

运用压力容器设计软件PV Elite 进行建模计算，可以得出地脚螺栓受力情况。方法（1）中k值取0.2，螺栓连接的相对刚度系数取0.25，残余预紧力F1分别以0.2F和0.6F进行计算，计算结果见表6。从表6 计算结果可知，方法（2）计算出的拧紧力矩在方法（1）的范围内，证明两种方法计算的结果是有效的。

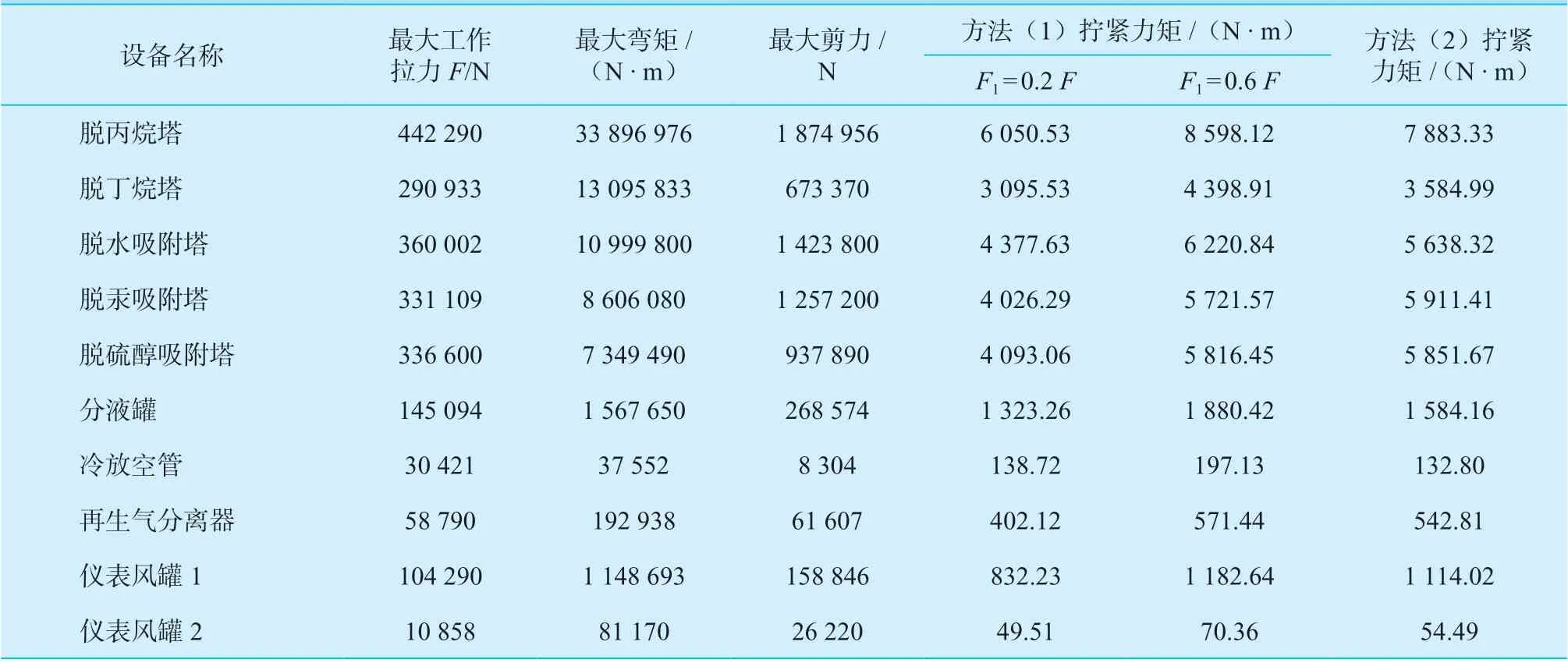
表6 拧紧力矩计算汇总Table 6 Summary of tightening torque calculation

2.2 材料屈服点比率σratio

从机械设计手册可知，一般规定拧紧后螺纹连接件预紧应力不得大于其材料的屈服点的80%。为了对比分析拧紧力矩，从材料屈服强度入手，引入材料屈服点比率σratio，反向推导拧紧力矩公式T=kF0d可得出其计算公式如下：

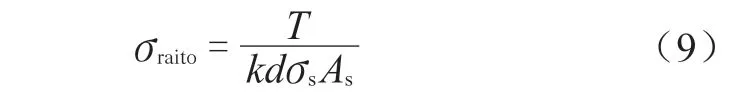
两种计算方法的材料屈服点比率σratio见表7。从表7 可知，材料屈服点比率σratio大于0.6 的为螺栓直径M56、M64、M72，σratio位于0.5～0.6 的螺栓算直径为M42、M48，σratio小于0.5 的螺栓算直径为M24、M36。可以得出，对于同一材料的螺栓，受力越大直径越大，σratio值越大。

2.3 工程项目中拧紧力矩的计算方法

机械设计手册中碳素钢螺栓取σratio=0.6 ～ 0.7，合金钢螺栓取σratio=0.5 ～ 0.6 来计算拧紧力矩，ASME PCC-1-2019 中取σratio=0.5 来计算拧紧力矩[9]。实际工程项目中，地脚螺栓通常会选取同一材料，通过螺栓数量和螺栓直径来防止螺栓失效，因此基于同一工程项目和同一材质的地脚螺栓的前提下，结合表7的分析结果，给出以下实际生产中计算拧紧力矩的建议（以计算复杂程度由高到低排序）：

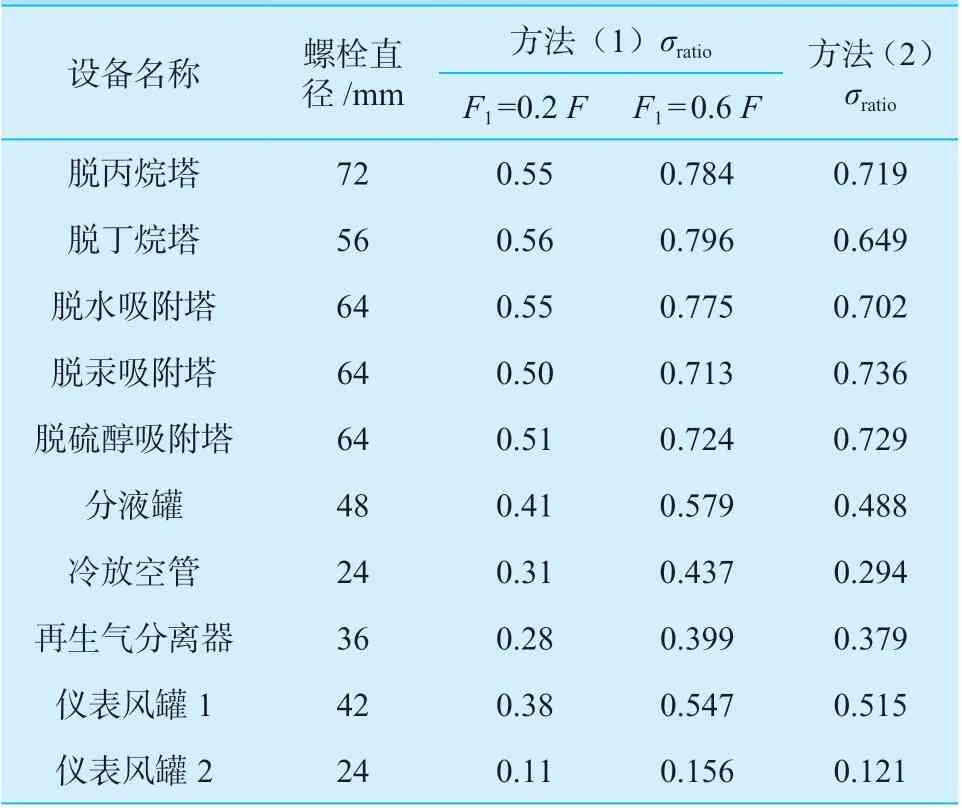
表7 材料屈服点比率σratioTable 7 Material yield point σratio

（1）大于M56 的地脚螺栓，采用理论计算法。此直径的螺栓受力大，材料屈服点比率σratio大于60%，因此需要运用计算方法（1）或方法（2），对地脚螺栓进行受力分析，再计算其拧紧力矩。

（2）大于M42 且小于M56 的地脚螺栓，采用标准给出的简化算法。此直径的地脚螺栓受力适中，材料屈服点比率σratio在0.5 ～ 0.6 之间，符合机械手册或ASME PCC-1-2019 标准中的简化算法，因此预紧力取0.5 ～ 0.6 倍材料屈服强度来计算拧紧力矩。

（3）小于M42 的地脚螺栓，采用查表法。此直径的地脚螺栓受力较小，材料屈服点比率σratio小于0.5，这是由于地脚螺栓材料的屈服强度远大于螺栓受力，所需的理论拧紧力矩小。采用标准SH/T 3538—2017、HG/T 20203—2017 和API RP 686—2009 的表格推荐值会大于理论计算值，但是推荐值是安全值，可以直接使用。

3 结束语

本文通过地脚螺栓受力分析进行拧紧力矩的计算，并引用俄罗斯标准SNIP 2.09.03 MDC 31-4.2000来相互印证，其中提出材料屈服点比率σratio，结合实际工程案例从而得出了塔式设备σratio的变化规律，以此提出理论计算法，标准简化算法，查表法并明确使用范围，以便实际生产中可以快速得到地脚螺栓拧紧力 矩。