波动方程在半无穷柱体和外部区域上的空间爆破和衰减性

李远飞,郭连红,曾 鹏

(广东财经大学华商学院 数据科学学院,广州 511300)

1 引言与预备知识

考虑如下单波动方程：

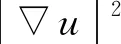
(1)

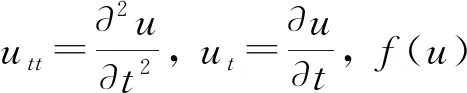
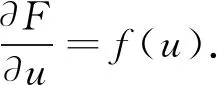
(2)

函数h(ut)满足

h(ut)ut≥0.

(3)

本文将函数ρ分为以下两种情形讨论：

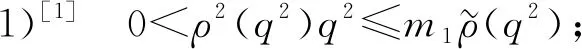
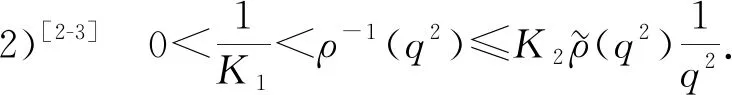
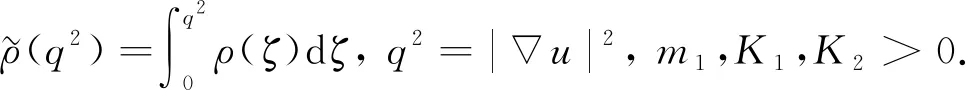
目前,关于偏微分方程解的衰减性研究已得到广泛关注[4-8]. 通常首先假设在柱体的无限端解趋于零或者趋于一个瞬态层流的先验假设,再利用能量估计的方法研究解空间的二择性. 但这种先验假设在实际应用中并不一定能得到充分满足. 因此,人们提出了Phragmén-Lindelöf型二择一研究,其不必假设方程组的解在无限端趋于零或趋于瞬态层流,而是证明调和函数随与有限端距离的增大或者呈指数(多项式)增长或者呈指数(多项式)衰减. 该方面的研究目前已有许多成果[9-20],包括拟线性和非线性问题[3,9-10]、Stoke方程[11-12]、浅水波方程[13]以及线性方程[14-15]等. 文献[16]将Phragmén-Lindelöf型二择一研究推广到了3种不同的无界区域上; 文献[1]研究了一类偏微分方程在一个球体外部区域上的空间二择性,证明了方程的解随球体的半径或者无限增长或者无限衰减,并通过设置参数证明了所得衰减率比文献中已有的其他结果更快.

受上述研究启发,本文首先在一个半无穷的柱体上考虑方程(1),其中方程的解在柱体的侧面上满足零边界条件. 与文献[3,12]不同,本文考虑ρ的两种不同情形,在每种情形下分别证明解的衰减率更快. 其次,本文将在半无穷柱体上所得结果推广到球体的外部区域上. 显然,本文模型比文献[1]的模型更复杂. 因此,文献[1]的方法并不能直接应用到本文中. 最后,本文讨论一类非线性弹性方程解的渐近性质.

2 柱体上的渐近性质

考虑方程(1)在半无穷柱体R上的渐近性质,这种区域是大多数研究者关注的情形[3,11]. 柱体R的母线平行于x3坐标轴,即

R={(x1,x2,x3)|(x1,x2)∈D,x3>0},

其中D是x1Ox2平面上的有界单连通区域,具有光滑的边界∂D. 令D(z)表示柱体R在x3=z处的截面,即

D(z)={(x1,x2,x3)|(x1,x2)∈D,x3=z>0}.

方程(1)的初边值条件为

其中T是一个大于零的常数，g是一个大于零的已知函数.

下面讨论在情形1)和情形2)下系统(1)-(4)-(5)-(6)的空间二择性,即证明方程的解随空间变量或者呈指数式增长或者呈指数式衰减. 解的指数式增长也称为解的空间blow-up,即解随空间变量趋近于无穷变得无界. 本文先定义一个能量表达式,然后利用微分不等式推出一个关于该能量表达式的一阶微分不等式,从而得到解的二择一结果. 计算：

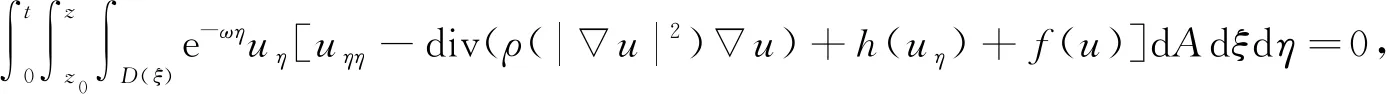
(7)

其中0≤z0≤z,ω是一个大于零的任意常数. 若定义

(8)

则在式(7)中利用散度定理可得

其中式(9)利用了式(2)及

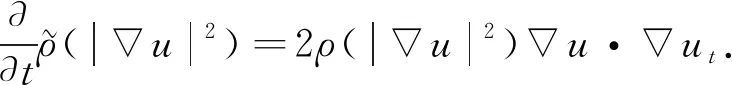
(10)

对式(9)求导,可得

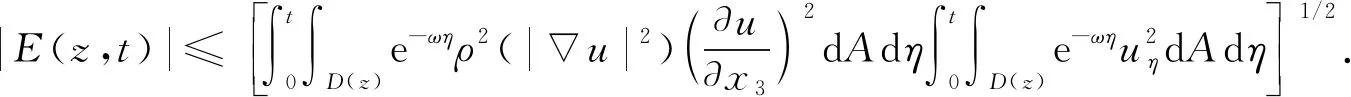
(12)

2.1 情形1)下的渐近性质

利用情形1)的条件和算术几何平均不等式,由式(12)可得

下面对式(13)分两种情形进行分析.

情形① ∃z0≥0,使得E(z0)≥0.

即

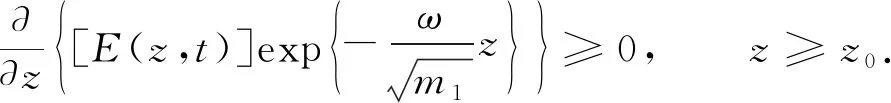
(14)

对式(14)从z0到z积分,可得

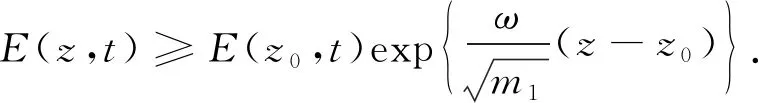
(15)

再结合式(9)和式(15),可得

情形② 对∀z≥0,都有E(z)<0.

此时,由式(12)可得

即

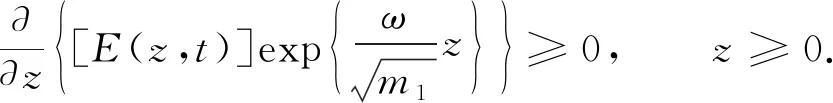
(17)

对式(17)从0到z积分,可得

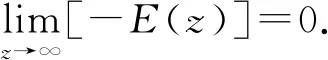
综上可得：

定理1设函数ρ满足情形1)及式(2)和式(3),则:

1) 如果存在z0≥0,使得E(z0,t)非负,则问题(1)-(4)-(5)-(6)不存在解;

2) 设u为问题(1)-(4)-(5)-(6)在一个半无穷柱体R上的解,如果对任意的z≥0,均有E(z,t)<0,则问题(1)-(4)-(5)-(6)的解u随空间变量呈指数式衰减,且满足式(18).

2.2 情形2)下的渐近性质

如果ρ满足情形2)的条件,此时,重新计算可得

将式(19)代入式(12),可得

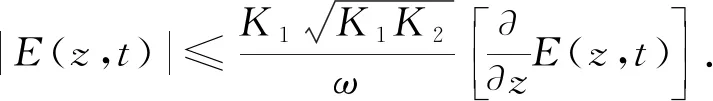
(20)

显然,式(20)与式(13)类似. 因此,采取类似分析可得如下结果.

定理2设函数ρ满足情形2)及式(2)和式(3). 则:

1) 如果存在z0≥0,使得E(z0,t)≥0,则问题(1)-(4)-(5)-(6)不存在解;

2) 设u为问题(1)-(4)-(5)-(6)在一个半无穷柱体R上的解,如果对任意的z≥0,均有E(z,t)<0,则问题(1)-(4)-(5)-(6)的解u随空间变量呈指数式衰减. 即或者

成立,或者

成立.

3 球体外部区域上的渐近性

受文献[1]启发,下面考虑一个球体的外部区域,表示为

令B(r)是以r为半径的球面,表示为

方程(1)的初边值条件为

3.1 情形1)下的渐近性质

先建立一个能量表达式

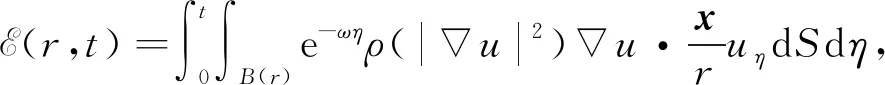
(24)

其中x=(x1,x2,x3). 令r0为一个大于零的常数,满足r>r0≥R0. 下面对E(r,t)从r0到r积分,利用散度定理、式(2),(3)及问题(1)-(22)-(23),可得

从而

再利用情形1)的条件、Hölder不等式和Young不等式,可得

类似2.1的分析,可得:

定理3设u为问题(1)-(22)-(23)在Ω上的解,其中函数ρ满足情形1)且式(2)和式(3)成立. 如果∃r0≥R0,使得E(r0,t)≥0,则

如果对∀r≥R0,均有E(r,t)<0,则问题(1)-(22)-(23)的解u随半径呈指数式衰减,即

3.2 情形2)条件下的渐近性质

假设ρ满足情形2)的条件. 此时,重新计算式(27)可得

对式(28)用类似2.2的分析,可得:

定理4设u为问题(1)-(4)-(5)-(6)在Ω上的解,其中函数ρ满足情形2)及式(2)和式(3). 如果∃r0≥R0,使得E(r0,t)≥0,则

如果对∀r≥R0,均有E(r,t)<0,则问题(1)-(4)-(5)-(6)的解u随半径呈指数式衰减,即

注1注意到文献[16]将柱体上的二择一研究推广到了二维锥形区域上,文献[21-22]研究了三维锥形区域的情形,定义的无界区域为

Ωa={(x1,x2,x3)|(x1,x2)∈Dx3,x3>a>0},

其中D(x3)是一个有界的依赖于x3的单连通平面区域,且平行于坐标平面x1Ox2. 例如,

由于Ωa的横截面与x3=z相关,而Poincaré不等式中的系数与界面D(x3)的面积和周长相关,所以文献[16,21-22]根据界面柱体舒张的情形考虑了几种无界区域,得到了解的空间二择性. 由于本文并未使用Poincaré不等式,所以定理1～定理4对区域Ωa均成立.

4 非线性弹性系统

下面考虑非线性弹性系统:

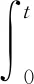
(29)

其中a,b是非负函数且a∈C1,b∈L∞,f和h分别满足式(2)和式(3),k0>0.g是可积函数且满足

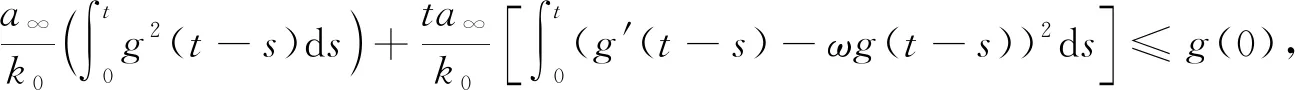
(30)

其中a∞=‖a(x)‖L∞.

文献[23]证明了方程(29)在一个有界区域上解随时间变量的一致衰减性; 文献[24-25]研究了方程(29)的几种特例,主要关注了解的适定性及关于时间变量的衰减性. 本文将上述结果推广到半无穷柱体区域和球面外部区域上.

4.1 半无穷柱体上的渐近性

在区域R×[0,T]上考虑方程(29),方程(29)满足初边值条件(4)-(5)-(6). 首先定义辅助函数

利用散度定理和方程(29)-(4)-(5)-(6),可得

由式(32)可得

利用Young不等式和Hölder不等式,可得

将式(34)和式(35)代入式(33),再利用式(30)可得

或

利用式(36)、Hölder不等式和Young不等式,可得

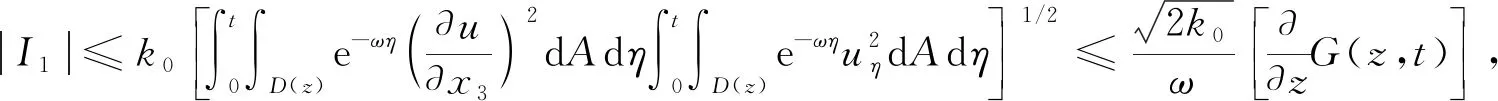
(38)

将式(38)和式(39)代入式(31),可得

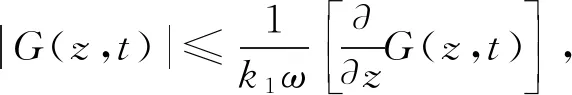
(40)

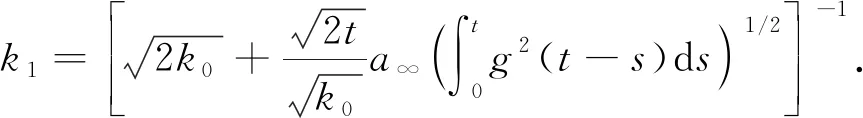
对式(40)进行分析,可得下列Phragmén-Lindelöf型二择一定理:

定理5设u为问题(29)-(4)-(5)-(6)在R上的解,其中式(30)成立. 如果∃z0≥0,使得E(z0,t)≥0,则

如果对∀z≥0,均有E(z,t)<0,则问题(29)-(4)-(5)-(6)的解u随空间变量呈指数式衰减,即成立

4.2 球体外部区域上的渐近性

假设方程(29)满足初边值条件(22)-(23). 首先,定义函数

类似4.1的计算,可得:

定理6设u为问题(29)-(22)-(23)在Ω上的解,其中式(30)成立. 如果∃r0≥R0,使得E(r0,t)≥0,则

如果对∀r≥R0,均有E(r,t)<0,则问题(29)-(22)-(23)的解u随空间变量呈指数式衰减,即成立

注2由于定理1～定理6中的解增长或衰减率都包含参数ω,而ω是一个大于零的任意常数. 因此,只要取ω足够大,则本文所得的衰减率比文献[2,5-6,20]中的衰减率更快.

注3本文所研究的模型更一般,因此本文的结果可向更简单的模型推广. 例如,波动方程[25]

utt-Δu+b(x)h(ut)=0

和弹性波动方程[26]

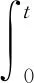
注4在衰减的情形下,要使衰减估计有意义,还需推导-E(0,t),-G(0,t),-E(R0,t)和-G(R0,t)的上界. 参照文献[7,14-15,18,20]中的全能量估计方法即可完成-E(0,t),-G(0,t)的上界估计.

5 -E(R0,t)和-G(R0,t)的上界估计

下面在衰减的情形下推导-E(R0,t)的上界. 由式(24)可得

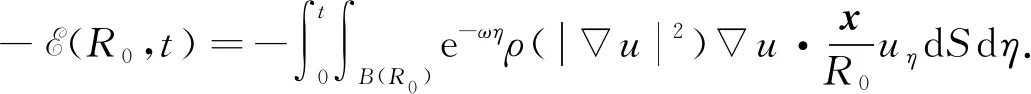
(41)

对式(26)从R0到∞积分,可得

设辅助函数

其中σ是一个大于零的常数. 显然S和u在x=R0上具有相同的边界条件. 在式(41)中利用散度定理、方程(1)和初边值条件(4)-(5)-(6),可得

利用Hölder不等式和Young不等式,可得

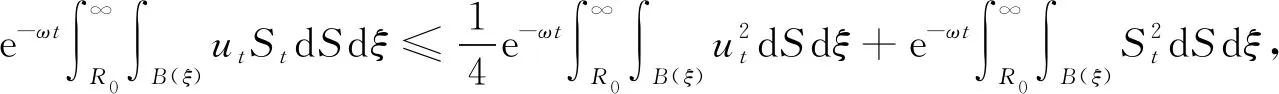
(44)

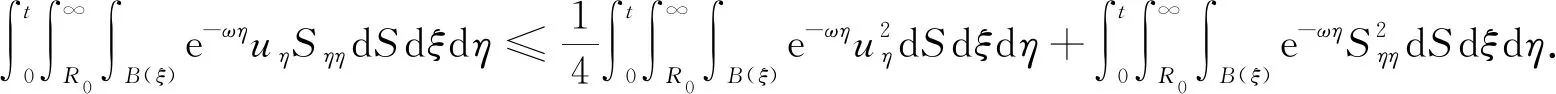
(45)

为控制式(43)的最后两项,需对h(ut)和f(u)做进一步假设. 设

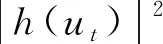
于是

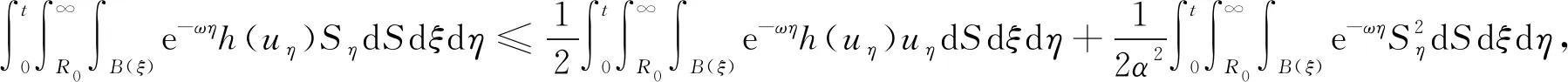
(46)

(47)

将式(44)～(47)代入式(43),再利用式(42)可得

由式(48)可得

于是证明了-E(R0,t)可由已知数据项控制.

注5同理可完成-G(R0,t)的上界估计. 能量表达式的导数由式(36)和式(37)定义,所以对-G(R0,t)的上界估计稍繁琐.

综上所述,本文用能量估计的方法研究了单波动方程在一个半无穷柱体和球体外部区域上的二择性. 通过设置一个大于零的参数,证明了本文取得的衰减或增长率比已有文献中的结果更快.