含参向量优化问题的Lipschitz连续性

孟 旭 东

(南昌航空大学科技学院，江西 共青城 332020)

0 引 言

最优化问题的各种最优值映射和最优解映射的定量分析是最优化理论和应用中的一个有趣而重要的课题.最优值映射或最优解映射往往具有一些几何性质，如Hölder连续性、Lipschitz连续性、平静性、可微性和次可微性等.它在模型表述、最优性描述、逼近理论，特别是对于无限维问题及数值程序中都有重要影响.因此，有必要从定量的角度对各种最优值映射或最优化问题的各种最优解映射得到一些结果.到目前为止，诸多文献讨论了扰动变分不等式、扰动平衡问题及扰动优化问题的连续性[1-11].研究各种问题解映射的连续性，可以丰富和发展运筹学的相关理论研究与算法设计，并能应用于资源分配、交通均衡、运筹管理及工程技术等众多领域.

然而，仅有少量文献研究了扰动优化问题的Hölder连续性和Lipschitz连续性[12-16].Li等在文献[12]中引入了目标函数的强凸性来分析扰动向量优化问题最优解映射的Hölder连续性.然而，有许多例子表明，扰动优化问题目标函数的强凸性是非常严格的.在文献[13]中，Li等得到了含参向量均衡问题近似解映射的Lipschitz连续性定理.Sadeqi等在文献[14]中分析了含参广义向量均衡问题近似有效解映射的Lipschitz连续性.在不具单调性的适当条件下，Han在文献[15]中讨论了含参广义向量均衡问题弱近似有效解映射和强近似有效解映射的Lipschitz连续性.在文献[16]中，孟旭东等在赋范线性空间中借助标量化方法研究了含参集值向量均衡问题近似解映射的Lipschitz连续性定理，作为应用，给出了向量问题近似解映射的Lipschitz连续的充分性条件.受以上诸多文献思想的启发，本文研究含参向量优化问题(弱)解映射和(弱)最优值映射的上(下)Lipschitz连续性.

1 准备工作

本文设X、Y、Λ、Ω为赋范空间，‖·‖和d(·，·)分别表示赋范空间中的范数和距离，BX、BY、BΛ、BΩ分别为X、Y、Λ、Ω中的闭单位球，C为Y中的闭凸点锥且C的拓扑内部int(C)≠∅.设D为Y中的非空子集，点y∈D，假若(D-y)∩(-int(C))=∅，则点y为D的弱有效点，假若(D-y)∩(-C)={0}，则点y为D的有效点，记集合D的所有弱有效点和有效点的全体分别为Ew(D)和E(D).

设f：X×Λ→Y为向量值映射，F：Ω→2X{∅}为非空集值映射，对每个点(λ，μ)∈Λ×Ω，讨论含参向量优化问题，简称为问题(PVOP).

(PVOP)minf(x，λ)，使得x∈F(μ)

(1)

设点(λ0，μ0)∈Λ×Ω给定，记f(·)=f(·，λ0)，F=F(μ0)，研究向量优化问题，简称为问题(VOP).

(VOP)minf(x)，使得x∈F

(2)

对任何的点(λ，μ)∈Λ×Ω，问题(PVOP)的弱最优值映射和最优值映射分别定义为

Vw(λ，μ)∶=Ew(f(F(μ)，λ))V(λ，μ)∶=E(f(F(μ)，λ))

对任何的点(λ，μ)∈Λ×Ω，问题(PVOP)的弱解映射和解映射分别定义为

Sw(λ，μ)∶={x∈F(μ)：f(x，λ)∈Vw(λ，μ)}S(λ，μ)∶={x∈F(μ)：f(x，λ)∈V(λ，μ)}

为研究方便起见，问题(VOP)的弱最优值映射、最优值映射、弱解映射及解映射分别记为Vw、V、Sw、S.

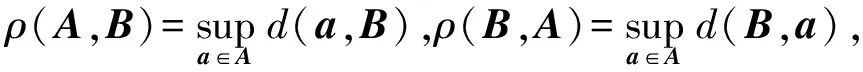
Graph(F)∶={(μ，x)∈Ω×X：x∈F(μ)}Dom(F)∶={μ∈Ω：F(μ)≠∅}

定义1设F：Ω→2X{∅}为非空集值映射，则

(1)映射F在点μ0∈Dom(F)周围关于常数hF>0，tF>0为Lipschitz连续的当且仅当对任何的点μ1，μ2∈μ0+tFBΩ，有

ρ(F(μ1)，F(μ2))≤hF‖μ1-μ2‖

(2)映射F在点μ0∈Dom(F)周围关于常数hF>0，tF>0为上Lipschitz连续的当且仅当对任何的点μ∈μ0+tFBΩ，有

ρ(F(μ)，F(μ0))≤hF‖μ-μ0‖

(3)映射F在点μ0∈Dom(F)周围关于常数hF>0，tF>0为下Lipschitz连续的当且仅当对任何的点μ∈μ0+tFBΩ，有

ρ(F(μ0)，F(μ))≤hF‖μ-μ0‖

(4)映射F在点(μ0，x0)∈Graph(F)周围关于常数hF>0，tF>0为伪Lipschitz连续的当且仅当存在点0∈X的邻域W0⊆X，使得对任何的点μ1，μ2∈μ0+tFBΩ，有

ρ(F(μ1)∩(x0+W0)，F(μ2))≤hF‖μ1-μ2‖

(5)映射F在点(μ0，x0)∈Graph(F)周围关于常数hF>0，tF>0为上伪Lipschitz连续的当且仅当存在点0∈X的邻域W0⊆X，使得对任何的点μ∈μ0+tFBΩ，有

ρ(F(μ)∩(x0+W0)，F(μ0))≤hF‖μ-μ0‖

(6)映射F在点(μ0，x0)∈Graph(F)周围关于常数hF>0，tF>0为下伪Lipschitz连续的当且仅当存在点0∈X的邻域W0⊆X，使得对任何的点μ∈μ0+tFBΩ，有

ρ(F(μ0)∩(x0+W0)，F(μ))≤hF‖μ-μ0‖

注1据定义1易知以下结论成立：

定义2设φ：Ω→X为向量值映射，则映射φ在点μ0∈Ω周围关于常数hφ>0，tφ>0为Lipschitz 连续当且仅当对任何的点μ1，μ2∈μ0+tφBΩ，有

‖φ(μ1)-φ(μ2)‖≤hφ‖μ1-μ2‖

定义3设f：X×Λ→Y为向量值映射，则

(1)问题(VOP)在Sw(或S)上关于常数hf>0具有锥全局控制性当且仅当对每个点x∈F，存在点x0∈Sw(或x0∈S)，使得

f(x)-f(x0)+hf‖x-x0‖BY⊆C

(3)

(2)问题(VOP)在Sw(或S)上关于常数hf>0具有内部锥全局控制性当且仅当对每个点x∈F，存在点x0∈Sw(或x0∈S)，使得

f(x)-f(x0)+hf‖x-x0‖BY⊆int(C)

(3)问题(VOP)在点x0∈Sw(或x0∈S)周围关于常数hf>0具有锥局部控制性当且仅当存在点x0的邻域U0⊆X，对每个点x∈F∩U0，存在点x0∈Sw∩U0(或x0∈S∩U0)，使得

f(x)-f(x0)+hf‖x-x0‖BY⊆C

(4)问题(VOP)在点x0∈Sw(或x0∈S)周围关于常数hf>0具有内部锥局部控制性当且仅当存在点x0的邻域U0⊆X，对每个点x∈F∩U0，存在点x0∈Sw∩U0(或x0∈S∩U0)，使得

以上笔者对文章开头、主体和结尾的分析，只是侧重于一点而言，其实不少文章的开头、主体和结尾所表现的特点是多方面的，学习时不能孤立和割裂。初中阶段课文阅读和作文练习的重点是记叙文，写记叙文有个好的开头和结尾，会使文章增色不少。所以上面就初中课本中部分记叙文的开头和结尾进行了重点分析，也顺便简单提到了文章的主体部分，供同学们写作时参考。

f(x)-f(x0)+hf‖x-x0‖BY⊆int(C)

注2(1)据定义3易知，(2)⟹(1)且(4)⟹(3).

(2)对任何的点y∈Y，定义‖y‖+∶=d(y，YC)，则式(3)可化为

hf‖x-x0‖≤‖f(x)-f(x0)‖+

(4)

2 问题(PVOP)的(弱)解映射的Lipschitz连续性

设f：X×Λ→Y为向量值映射，F：Ω→2X{∅}为非空集值映射，为研究问题叙述方便起见，给出以下基本假设(A).

(A1)问题(PVOP)的弱解集在给定点(λ0，μ0)∈Dom(Sw)的某邻域内；

(A2)问题(PVOP)的解集在给定点(λ0，μ0)∈Dom(S)的某邻域内；

(A3)映射F在点μ0∈Dom(F)周围关于常数hF>0，tF>0具有Lipschitz连续性；

(A4)问题(VOP)在Sw上关于常数hf>0具有锥全局控制性；

(A4′)问题(VOP)在Sw上关于常数hf>0具有内部锥全局控制性；

(A5)问题(VOP)在S上关于常数hf>0具有锥全局控制性；

(A5′)问题(VOP)在S上关于常数hf>0具有内部锥全局控制性；

(A6)对任何的点λ∈Λ，f(·，λ)在X上关于常数mf>0具有Lipschitz连续性，且对任何的点x∈X，f(x，·)在点λ0∈Λ周围关于常数nf>0，tf>0具有Lipschitz连续性；

(A7)映射F在点(μ0，x0)∈Graph(F)周围关于点0∈X的邻域U0⊆X及常数hF>0，tF>0具有上伪Lipschitz连续性和下伪Lipschitz连续性；

(A8)对假设(A7)中的邻域U0⊆X，问题(VOP)在点x0∈Sw周围关于点0∈X的邻域Q0⊆X，满足Q0+Q0⊆U0及hf>0具有锥局部控制性；

(A8′)对假设(A7)中的邻域U0⊆X，问题(VOP)在点x0∈Sw周围关于点0∈X的邻域Q0⊆X，满足Q0+Q0⊆U0及hf>0具有内部锥局部控制性；

(A9)对假设(A7)中的邻域U0⊆X，问题(VOP)在点x0∈S周围关于点0∈X的邻域Q0⊆X，满足Q0+Q0⊆U0及hf>0具有锥局部控制性；

(A9′)对假设(A7)中的邻域U0⊆X，问题(VOP)在点x0∈S周围关于点0∈X的邻域Q0⊆X，满足Q0+Q0⊆U0及hf>0具有内部锥局部控制性；

(A10)对假设(A7)中的邻域U0⊆X，对任何的点x∈x0+U0，f(x，·)在点λ0∈Λ周围关于常数tf>0，nf>0具有Lipschitz连续性，且对任何的点λ∈λ0+tfBΛ，f(·，λ)在U0上关于常数mf>0具有Lipschitz连续性.

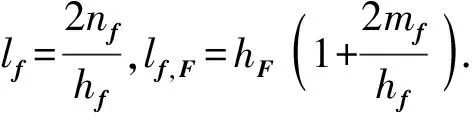
定理1对问题(PVOP)而言，若假设(A1)、(A3)、(A4)与(A6)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为上Lipschitz 连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw(λ，μ)，Sw)≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

(5)

证明任取点x(λ，μ)∈Sw(λ，μ)，其中λ∈λ0+tfBΛ，μ∈μ0+tFBΩ.据Sw(λ，μ)的定义知

x(λ，μ)∈F(μ)且f(x，λ)-f(x(λ，μ)，λ)∉-int(C)，∀x∈F(μ)

(6)

据假设(A3)知，存在点x(μ0)∈F(μ0)，使得

‖x(λ，μ)-x(μ0)‖≤hF‖μ-μ0‖

(7)

据假设(A4)知，对以上的点x(μ0)，存在点x(λ0，μ0)∈Sw，使得

f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)+

hf‖x(μ0)-x(λ0，μ0)‖BY⊆C

(8)

不失一般性，不妨假设x(μ0)≠x(λ0，μ0)，f(x(μ0)，λ0)≠f(x(λ0，μ0)，λ0).易见点x(λ0，μ0)∈F(μ0)，结合假设(A3)知，存在点x(μ)∈F(μ)，使得

‖x(λ0，μ0)-x(μ)‖≤hF‖μ-μ0‖

(9)

则有

f(x(μ)，λ)-f(x(λ，μ)，λ)=f(x(λ0，μ0)，λ0)-

f(x(μ0)，λ0)+

w(λ，μ)

(10)

其中

w(λ，μ)=f(x(μ)，λ)-f(x(λ0，μ0)，λ)+

f(x(λ0，μ0)，λ)-f(x(λ0，μ0)，λ0)+

f(x(μ0)，λ0)-f(x(μ0)，λ)+

f(x(μ0)，λ)-f(x(λ，μ)，λ)

由假设(A6)，知

‖w(λ，μ)‖≤mf‖x(μ)-x(λ0，μ0)‖+

mf‖x(μ0)-x(λ，μ)‖+

2nf‖λ-λ0‖

结合式(7)、(9)，得

‖w(λ，μ)‖≤2mfhF‖μ-μ0‖+2nf‖λ-λ0‖

(11)

则必有

‖f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)‖+≤‖w(λ，μ)‖

(12)

事实上，假若‖f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)‖+>‖w(λ，μ)‖，据‖·‖+的定义知

f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)+

‖w(λ，μ)‖BY⊆int(C)

(13)

(1)若‖w(λ，μ)‖=0，则w(λ，μ)=0，由式(8)、(10)，知

f(x(μ)，λ)-f(x(λ，μ)，λ)∈-int(C)

这与式(6)矛盾.

f(x(λ，μ)，λ)-f(x(μ)，λ)=f(x(μ0)，λ0)-

f(x(λ0，μ0)，λ0)+

‖w(λ，μ)‖·

并结合式(13)，得

f(x(λ，μ)，λ)-f(x(μ)，λ)∈int(C)

这与式(6)矛盾.由式(8)、(11)～(13)，有

hf‖x(μ0)-x(λ0，μ0)‖≤‖f(x(μ0)，λ0)-

f(x(λ0，μ0)，λ0)‖+≤

2mfhF‖μ-μ0‖+

2nf‖λ-λ0‖

故

(14)

结合式(6)、(14)，得

d(x(λ，μ)，Sw)≤‖x(λ，μ)-x(λ0，μ0)‖≤

‖x(λ，μ)-x(μ0)‖+

‖x(μ0)-x(λ0，μ0)‖≤

lf‖μ-μ0‖+lf，F‖λ-λ0‖

注意到点x(λ，μ)∈Sw(λ，μ)的任意性知式(5)成立.

据定理1，结合注2的(1)知

推论1对问题(PVOP)而言，假若假设(A1)、(A3)、(A4′)与(A6)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为上Lipschitz 连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw(λ，μ)，Sw)≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

类似定理1的论证过程可知

定理2对问题(PVOP)而言，假若假设(A2)、(A3)、(A5)与(A6)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S(λ，μ)，S)≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

据定理2，结合注2的(1)知

推论2对问题(PVOP)而言，假若假设(A2)、(A3)、(A5′)与(A6)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S(λ，μ)，S)≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

定理3对问题(PVOP)而言，假若假设(A1)、(A7)、(A8)与(A10)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(Sw)周围关于常数tf>0，tF>0为上Lipschitz 连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw(λ，μ)∩(x0+W0)，Sw)≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

(15)

证明设W0⊆X为点0∈X的任何邻域，满足W0+hFtFBX⊆Q0，则W0为点0∈X在X中的理想邻域.事实上，对任何的点x(λ，μ)∈Sw(λ，μ)∩(x0+W0)，λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，据映射F的上伪Lipschitz连续性知，存在点x(μ0)∈F(μ0)，使得

‖x(λ，μ)-x(μ0)‖≤hF‖μ-μ0‖≤hFtF

(16)

则有

x(μ0)-x0=(x(μ0)-x(λ，μ))+(x(λ，μ)-x0)∈

hFtFBX+W0⊆Q0

故点x(μ0)∈F(μ0)∩(x0+Q0)，据假设(A8)知存在点x(λ0，μ0)∈Sw∩(x0+Q0)，使得

f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)+

hf‖x(μ0)-x(λ0，μ0)‖BY⊆C

(17)

不失一般性，不妨假设x(μ0)≠x(λ0，μ0)，f(x(μ0)，λ0)≠f(x(λ0，μ0)，λ0).易见点x(λ0，μ0)∈F(μ0)∩(x0+Q0)，由F的下伪Lipschitz连续性知存在点x(μ)∈F(μ)，使得

‖x(λ0，μ0)-x(μ)‖≤hF‖μ-μ0‖≤hFtF

(18)

则有

x(μ0)-x0=(x(μ0)-x(λ0，μ0))+(x(λ0，μ0)-

x0)∈hFtFBX+W0⊆Q0⊆U0

且

f(x(μ)，λ)-f(x(λ，μ)，λ)=f(x(λ0，μ0)，λ0)-

f(x(μ0)，λ0)+

w(λ，μ)

其中

w(λ，μ)=f(x(μ)，λ)-f(x(λ0，μ0)，λ)+

f(x(λ0，μ0)，λ)-f(x(λ0，μ0)，λ0)+

f(x(μ0)，λ0)-f(x(μ0)，λ)+

f(x(μ0)，λ)-f(x(λ，μ)，λ)

由假设(A10)，知

‖w(λ，μ)‖≤mf‖x(μ)-x(λ0，μ0)‖+

mf‖x(μ0)-x(λ，μ)‖+

2nf‖λ-λ0‖

结合式(16)、(18)，得

‖w(λ，μ)‖≤2mfhF‖μ-μ0‖+2nf‖λ-λ0‖

(19)

类似于定理1的论证过程有

‖f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)‖+≤‖w(λ，μ)‖

(20)

由式(17)、(19)、(20)，知

hf‖x(μ0)-x(λ0，μ0)‖≤2mfhF‖μ-μ0‖+

2nf‖λ-λ0‖

故

(21)

结合式(16)、(21)，得

lf‖μ-μ0‖+lf，F‖λ-λ0‖

再据点x(λ，μ)∈Sw(λ，μ)的任意性知式(15)成立.

据定理3，结合注2的(1)知

推论3对问题(PVOP)而言，假若假设(A1)、(A7)、(A8′)与(A10)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(Sw)周围关于常数tf>0，tF>0为上Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw(λ，μ)∩(x0+W0)，Sw)≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

类似定理3的证明过程易知

定理4对问题(PVOP)而言，假若假设(A2)、(A7)、(A9)与(A10)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(S)周围关于常数tf>0，tF>0为上Lipschitz 连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S(λ，μ)∩(x0+W0)，S)≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

据定理4，结合注2的(1)知

推论4对问题(PVOP)而言，假若假设(A2)、(A7)、(A9′)与(A10)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(S)周围关于常数tf>0，tF>0为上Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S(λ，μ)∩(x0+W0)，S)≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

类似于问题(PVOP)的弱解映射和解映射的上Lipschitz连续性的充分性条件，结合注2的(1)易得问题(PVOP)的弱解映射和解映射的下Lipschitz连续性定理.

定理5对问题(PVOP)而言，假若假设(A1)、(A3)、(A4)与(A6)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为下Lipschitz 连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw，Sw(λ，μ))≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

推论5对问题(PVOP)而言，假若假设(A1)、(A3)、(A4′)与(A6)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为下Lipschitz 连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw，Sw(λ，μ))≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

定理6对问题(PVOP)而言，假若假设(A2)、(A3)、(A5)与(A6)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S，S(λ，μ))≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

推论6对问题(PVOP)而言，假若假设(A2)、(A3)、(A5′)与(A6)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S，S(λ，μ))≤lf‖λ-λ0‖+lf，F‖μ-μ0‖

定理7对问题(PVOP)而言，假若假设(A1)、(A7)、(A8)与(A10)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(Sw)周围关于常数tf>0，tF>0为下Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw，Sw(λ，μ)∩(x0+W0))≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

推论7对问题(PVOP)而言，假若假设(A1)、(A7)、(A8′)与(A10)成立，则问题(PVOP)的弱解映射Sw：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(Sw)周围关于常数tf>0，tF>0为下Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Sw，Sw(λ，μ)∩(x0+W0))≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

定理8对问题(PVOP)而言，假若假设(A2)、(A7)、(A9)与(A10)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S，S(λ，μ)∩(x0+W0))≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

推论8对问题(PVOP)而言，假若假设(A2)、(A7)、(A9′)与(A10)成立，则问题(PVOP)的解映射S：Λ×Ω→2X{∅}在点((λ0，μ0)，x0)∈Graph(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即存在点0∈X的邻域W0⊆X，对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(S，S(λ，μ)∩(x0+W0))≤lf‖λ-λ0‖+

lf，F‖μ-μ0‖

3 问题(PVOP)的(弱)最优值映射的Lipschitz连续性

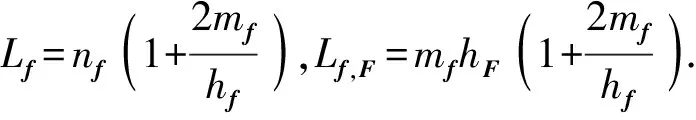
定理9对问题(PVOP)而言，假若假设(A1)、(A3)、(A4)与(A6)成立，则问题(PVOP)的弱最优值映射Vw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Vw(λ，μ)，Vw)≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

(22)

证明任取点f(x(λ，μ)，λ)∈Vw(λ，μ)，其中λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，则点x(λ，μ)∈F(μ)，且存在点x(μ0)∈F(μ0)，使得

‖x(λ，μ)-x(μ0)‖≤hF‖μ-μ0‖

(23)

据假设(A4)知，对以上的点x(μ0)，存在点x(λ0，μ0)∈Sw，使得

f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)+

hf‖x(μ0)-x(λ0，μ0)‖BY⊆C

据f(·，λ0)的Lipschitz连续性知

f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)+

(24)

又x(λ0，μ0)∈F(μ0)，结合假设(A3)知，存在点x(μ)∈F(μ)，使得

‖x(λ0，μ0)-x(μ)‖≤hF‖μ-μ0‖

(25)

显然

f(x(μ)，λ)-f(x(λ，μ)，λ)=f(x(λ0，μ0)，λ0)-

f(x(μ0)，λ0)+

w(λ，μ)

其中

w(λ，μ)=f(x(μ)，λ)-f(x(λ0，μ0)，λ)+

f(x(λ0，μ0)，λ)-f(x(λ0，μ0)，λ0)+

f(x(μ0)，λ0)-f(x(μ0)，λ)+

f(x(μ0)，λ)-f(x(λ，μ)，λ)

由假设(A6)，知

‖w(λ，μ)‖≤mf‖x(μ)-x(λ0，μ0)‖+

mf‖x(μ0)-x(λ，μ)‖+

2nf‖λ-λ0‖

结合式(23)、(25)，得

‖w(λ，μ)‖≤2mfhF‖μ-μ0‖+2nf‖λ-λ0‖

(26)

类似定理1的证明过程有

‖f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)‖+≤‖w(λ，μ)‖

(27)

由式(24)、(26)、(27)，知

2mfhF‖μ-μ0‖+2nf‖λ-λ0‖

故

‖f(x(μ0)，λ0)-f(x(λ0，μ0)，λ0)‖≤

(28)

结合式(23)、(28)，有

d(f(x(λ，μ)，λ)，Vw)≤‖f(x(λ，μ)，λ)-

f(x(λ0，μ0)，λ0)‖≤

‖f(x(λ，μ)，λ)-

f(x(μ0)，λ)‖+

‖f(x(μ0)，λ)-

f(x(λ0，μ0)，λ0)‖+

‖f(x(μ0)，λ0)-

f(x(λ0，μ0)，λ0)‖≤

Lf‖μ-μ0‖+

Lf，F‖λ-λ0‖

再由点x(λ，μ)∈Sw(λ，μ)的任意性知式(22)成立.

据定理9，结合注2的(1)知

推论9对问题(PVOP)而言，假若假设(A1)、(A3)、(A4′)与(A6)成立，则问题(PVOP)的弱最优值映射Vw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Vw(λ，μ)，Vw)≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

类似定理9的论证过程易得

定理10对问题(PVOP)而言，假若假设(A2)、(A3)、(A5)与(A6)成立，则问题(PVOP)的最优值映射V：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(V(λ，μ)，V)≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

据定理10，结合注2的(1)知

推论10对问题(PVOP)而言，假若假设(A2)、(A3)、(A5′)与(A6)成立，则问题(PVOP)的最优值映射V：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为上Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(V(λ，μ)，V)≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

类似于问题(PVOP)的弱最优值映射和最优值映射的上Lipschitz连续性定理的讨论过程，结合注2的(1)可得问题(PVOP)的弱最优值映射和最优值映射的下Lipschitz连续性基本定理.

定理11对问题(PVOP)而言，假若假设(A1)、(A3)、(A4)与(A6)成立，则问题(PVOP)的弱最优值映射Vw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Vw，Vw(λ，μ))≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

推论11对问题(PVOP)而言，假若假设(A1)、(A3)、(A4′)与(A6)成立，则问题(PVOP)的弱最优值映射Vw：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(Sw)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(Vw，Vw(λ，μ))≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

定理12对问题(PVOP)而言，假若假设(A2)、(A3)、(A5)与(A6)成立，则问题(PVOP)的最优值映射V：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(V，V(λ，μ))≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

推论12对问题(PVOP)而言，假若假设(A2)、(A3)、(A5′)与(A6)成立，则问题(PVOP)的最优值映射V：Λ×Ω→2X{∅}在点(λ0，μ0)∈Dom(S)周围关于常数tf>0，tF>0为下Lipschitz连续的，即对任何的点λ∈λ0+tfBΛ，μ∈μ0+tFBΩ，有

ρ(V，V(λ，μ))≤Lf‖λ-λ0‖+Lf，F‖μ-μ0‖

4 结 语

在目标函数和可行集分别受参数扰动的情况下，在适当假设条件下，在赋范空间中建立了含参向量优化问题(弱)解映射和(弱)最优值映射的上(下)Lipschitz连续性充分性基本定理.研究表明，(弱)解映射和(弱)最优值映射的上(下)Lipschitz 连续的充分性条件均具有统一性规律，有利于建立含参向量优化问题解映射的Hölder连续性的统一规律，有利于分析各类含参向量优化问题解映射的Hölder连续性和Lipschitz连续性的统一框架结构，并为研究含参向量优化问题解映射的稳定性奠定基础.