第三方物流服务商选择研究——基于犹豫模糊TOPSIS方法

郭 敏， 梁海天

（中北大学经济与管理学院，太原 030051）

犹豫模糊集可以很好地克服群决策过程中出现的犹豫性、模糊性. 1995年Zadeh［1］首次提出了传统的模糊集概念，从此模糊集理论就广泛地应用于各个领域. 但随着社会的发展，人们所处环境及遇到的问题也更加复杂，传统的模糊集已经无法完整的描述所研究的决策问题，为此Atanassov［2-4］引入隶属度来表达不确定的思想. Atanassov认为，传统模糊集的隶属度只能用处于0～1之间的某个确切的数来表示，无法更进一步地了解决策者在实际决策过程中的模糊程度. 基于以上考虑，Atanassov研究了隶属度、非隶属度和犹豫度3个维度，并定义了三者之间的关系，进而提出直觉模糊集概念，这一概念被广泛运用到逻辑规划［5］、群决策［4-7］等诸多领域.

随着研究的深入，人们发现直觉模糊集理论和区间直觉模糊集理论并不能够灵活地刻画出决策者给出的多个可能值. 因此，西班牙学者Torra和Narukawa［8］在2009年提出了犹豫模糊集的概念，它的隶属度不是某个值或者服从一定分布，而是多个可能值，与传统的模糊集和直觉模糊集理论相比，犹豫模糊集能更加灵活地描述决策者在决策过程中对于事物信息不确定的状况. 犹豫模糊集不需要构造隶属度函数，且表达比较方便，因此受到学者们的关注. TOPSIS是求解多准则问题的经典方法，它的思想是最接近正理想点且最远离负理想点的解，即为最优解［9］. 然而在传统的TOPSIS中，属性值和权重均为固定值，这与现实群决策环境当中的不确定性并不相符，因此学者开始将模糊集理论与拓展形式的TOPSIS方法结合进行研究. 以前对第三方物流服务商的选择研究多是利用直觉模糊集理论进行阐述的，Kumar和Chen［10］提出了用直觉模糊集理论对第三方物流服务商进行选择. 此研究侧重对第三方物流服务商评价指标的选择，运用直觉模糊集理论将评价指标的语言形式转化为模糊形式的语言进行选取，但是这些研究侧重的是对第三方物流服务商评价指标进行模糊化的选取. 并没有说明如何有效的选取第三方物流服务商，基于以上研究，Xu［11］提出犹豫模糊TOPSIS方法来解决权重信息不足的问题，Chu等［12］将模糊集理论与TOPSIS相结合，用来解决群决策过程中选取服务商的问题，而后Ashtiani 等［13］进行了更深入的研究，提出了属性值和准则权重均为区间数的TOPSIS方法. Lan［14］提出一种基于TOPSIS方法的新方法，用来解决准则值为犹豫模糊数且准则权重部分已知的多准则决策问题. 上述研究都是基于属性权重值整体或部分已知以及在求模糊数间的距离时主观添加了隶属值的情况，然而在现实的决策过程当中属性权重值是不确定的.

本文提出一种新的基于犹豫模糊TOPSIS方法选择第三方物流服务商的决策方法. 首先，考虑到决策者的认知能力和对事物的不同偏好，通过犹豫模糊熵的熵权法来确定属性的权重值；其次，为了避免在求方案和正负理想解的距离时主观添加隶属值，采用了计算犹豫模糊属性权重与每个方案的犹豫模糊准则值到正负理想解对应的准则值的排序加权Hausdorff 距离的方法，求得各备选物流服务商与正负理想解之间的距离；最后，利用TOPSIS的决策方法对各个备选物流服务商的优劣势进行排序，并通过实例进行验证.

1 基础理论

1.1 犹豫模糊集

1.2 犹豫模糊元［15-16］

1.3 犹豫模糊元的得分函数

1.4 犹豫模糊数间的排序加权

Hausdorff的距离为

1.5 犹豫模糊熵

定义4［18］对于任意一个犹豫模糊数h，它的犹豫模糊熵为

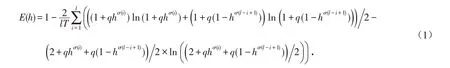
式中：hσ(i)为第i 大的元素，并且q>0;j=1,2,…,n;T=(1+q)ln(1+q)-(2+q)( ln(2+q)-ln 2 ).

2 犹豫模糊下TOPSIS方法的问题描述和模型构建

2.1 问题描述［19］

2.2 权重的确定

信息熵描述了系统的无序程度，指标的信息熵越小，表示不同程度越大，所包含的信息越多，应赋予这个指标更大的权重［20］. 将熵的概念引入模糊集理论中，从而产生了模糊熵. 在多属性决策中，评价的属性一般划分为效益型和成本型，熵权法确定犹豫模糊属性权重的方法如下：

步骤1［21］将决策者给出的方案xi在属性dj的属性值用犹豫模糊数hij表示.

步骤3［21］用模糊熵计算出各个评价指标的熵Ej.

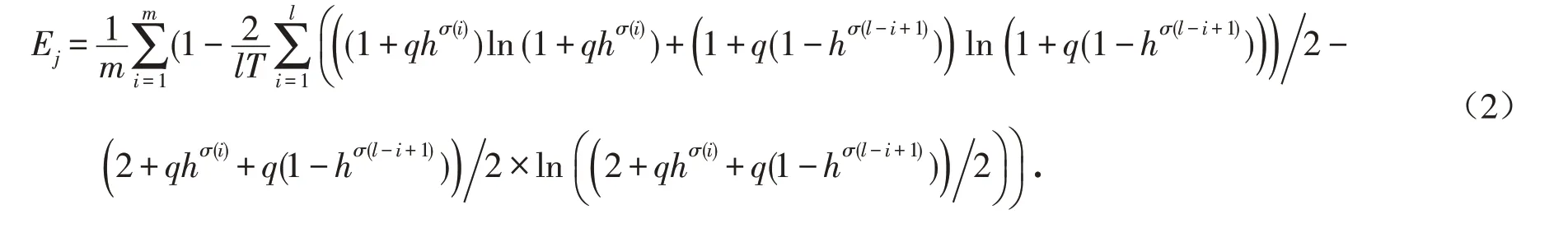
式中：hσ(i)为第i 大的元素，并且q>0;j=1,2,…,n;T=(1+q)ln(1+q)-(2+q)( ln(2+q)-ln 2 ).

步骤4［21］第j 个评价指标的熵权为

3 犹豫模糊TOPSIS方法的排序步骤

步骤1 根据专家决策信息，犹豫模糊决策矩阵M 表示为

将犹豫模糊数的元素按递增顺序排列，并将元素相对较少的犹豫模糊数按照Xu等［17］给出的展开规则进行扩展处理.

步骤2 对标准化犹豫模糊决策矩阵M 进行归一化处理，消除各指标的量纲与数量级的影响，得到归一化犹豫模糊决策矩阵［22］

步骤4 定义正、负理想解如下：

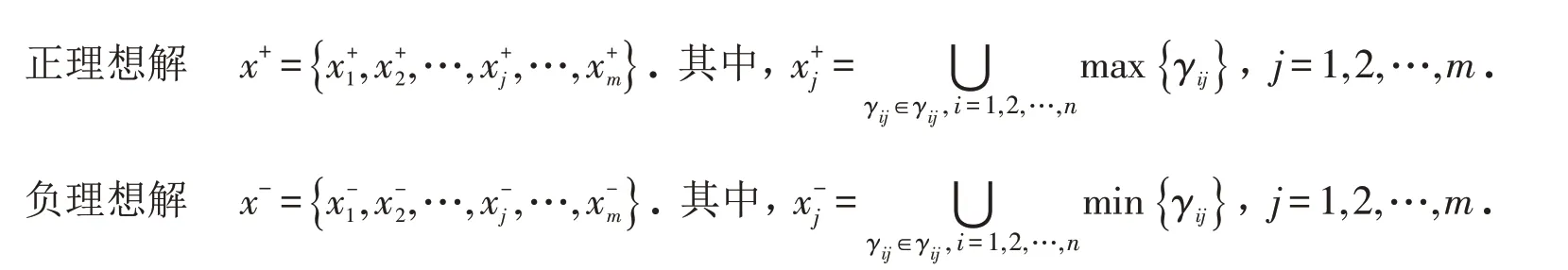
步骤5 将犹豫模糊属性权重与每个方案的犹豫模糊准则值到正负理想解对应的准则值的排序加权Hausdorff距离结合起来构成犹豫模糊排序加权距离

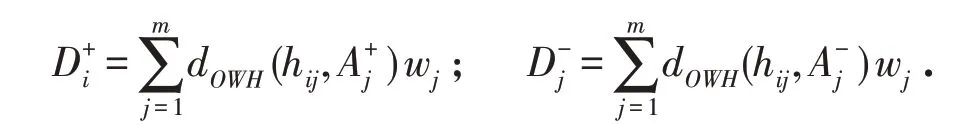
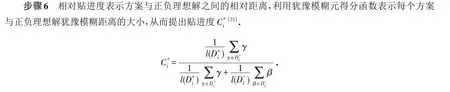
4 犹豫模糊TOPSIS方法在第三方物流服务商选择中的案例分析

4.1 问题的分析

选择高质量的第三方物流公司是一个企业生存发展的关键，对物流企业各个方面进行合理的评估是选择优质服务商的前提. 假如现在有5家第三方物流服务商，分别表示为{x1,x2,x3,x4,x5}. 为了选择最优的物流服务商，某企业从高效型角度出发提出了4个评价指标，即C1送达时间、C2增值服务能力、C3货损率、C4顾客满意度（表1）. 其中，C1和C3是成本型评价指标，C2和C4是效益型评价指标. 相应的权重w=(w1,w2,w3,w4)未知，决策者的指标偏好系数满足{λ1,λ2,λ3,λ4} ={0 .35,0.35,0.15,0.15} .

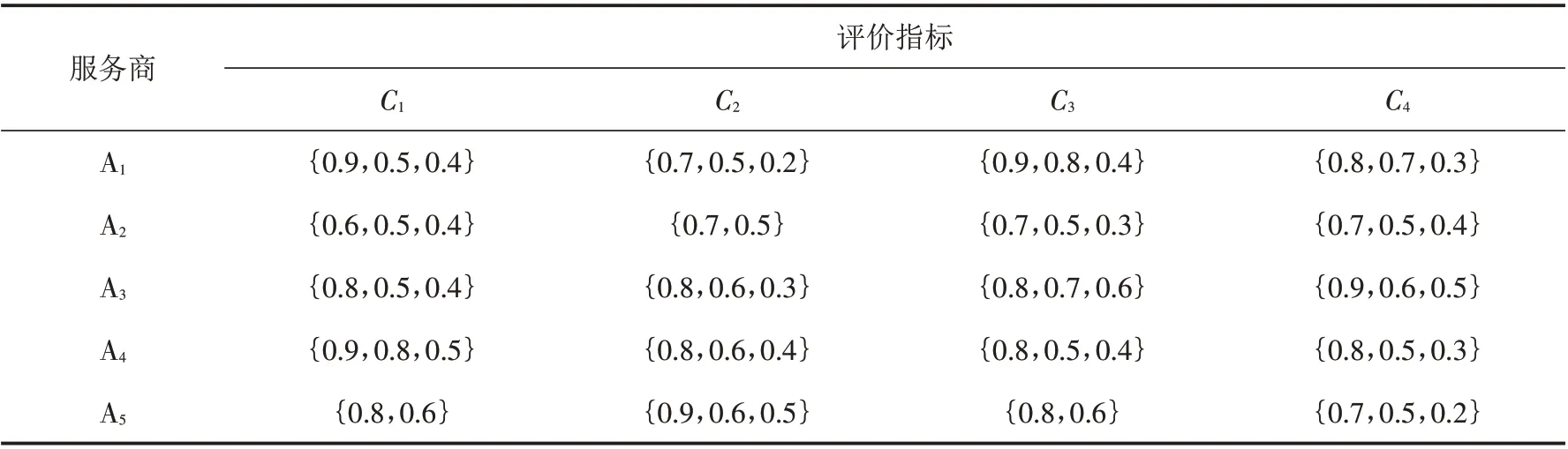
表1 犹豫模糊决策矩阵Tab.1 Hesitant fuzzy decision matrix

4.2 权重的确定

通过前面犹豫模糊熵的权重确定方法，用公式（1）计算w 的属性权重值. 假设q=2，可得熵权矩阵，如表2.

根据公式（2）可得E(1)=0.914 7、E(2)=0.839 7、E(3)=0.839 2、E(4)=0.900 3，所以熵权w*=(0.332 7,0.298 9,0.136 9,0.159 1) .

根据步骤2，把C1和C3转化为效益型指标可得归一化犹豫模糊决策矩阵Mˉ，如表3.

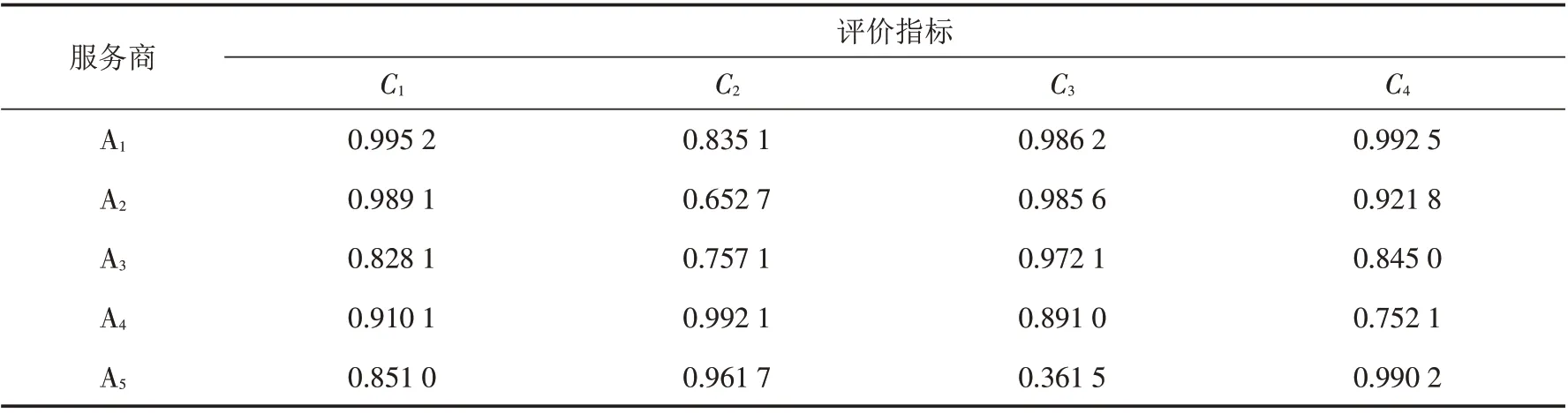
表2 犹豫模糊熵矩阵Tab.2 Hesitant fuzzy entropy matrix

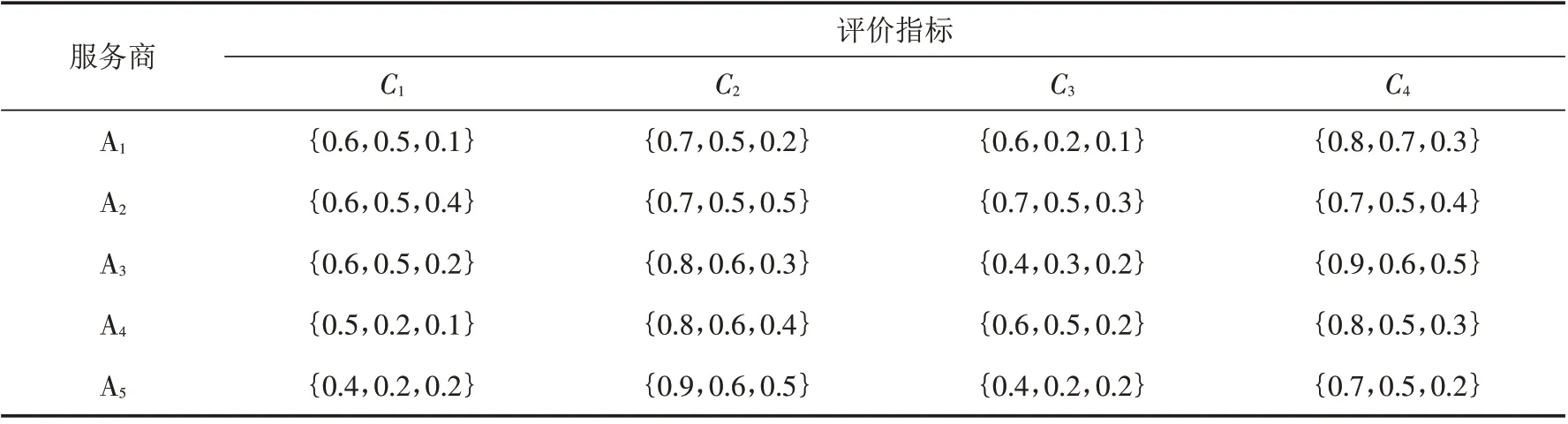
表3 犹豫模糊决策矩阵Tab.3 Hesitant fuzzy decision matrix

根据步骤3，可得加权归一化犹豫模糊矩阵：

根据步骤4，可得正理想解、负理想解分别为：

根据步骤5可得正负排序加权Hausdorff距离表4和表5.

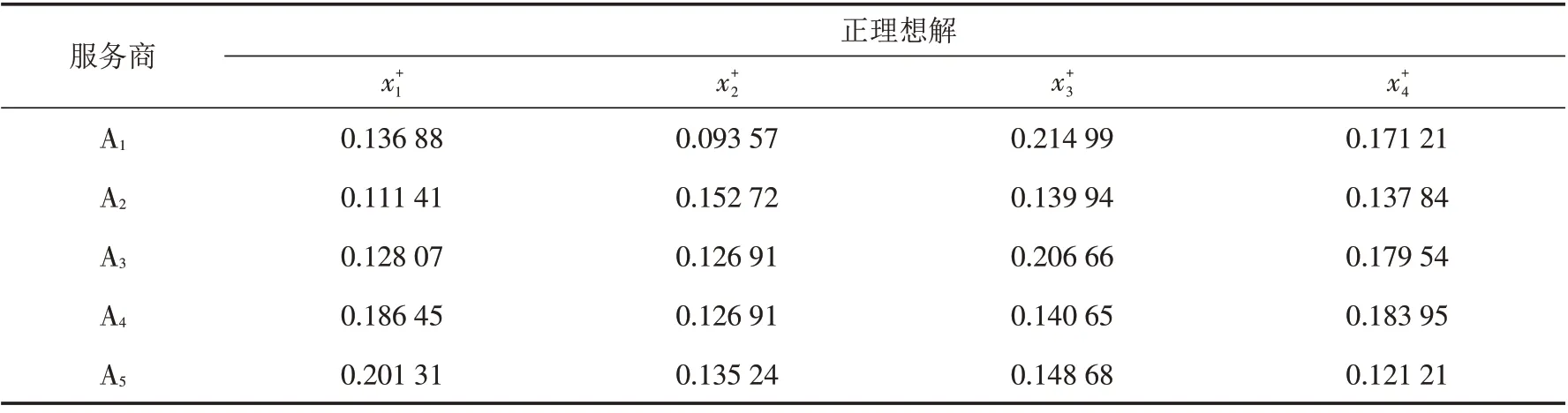
表4 正排序加权距离Tab.4 Positive sort weighted distance

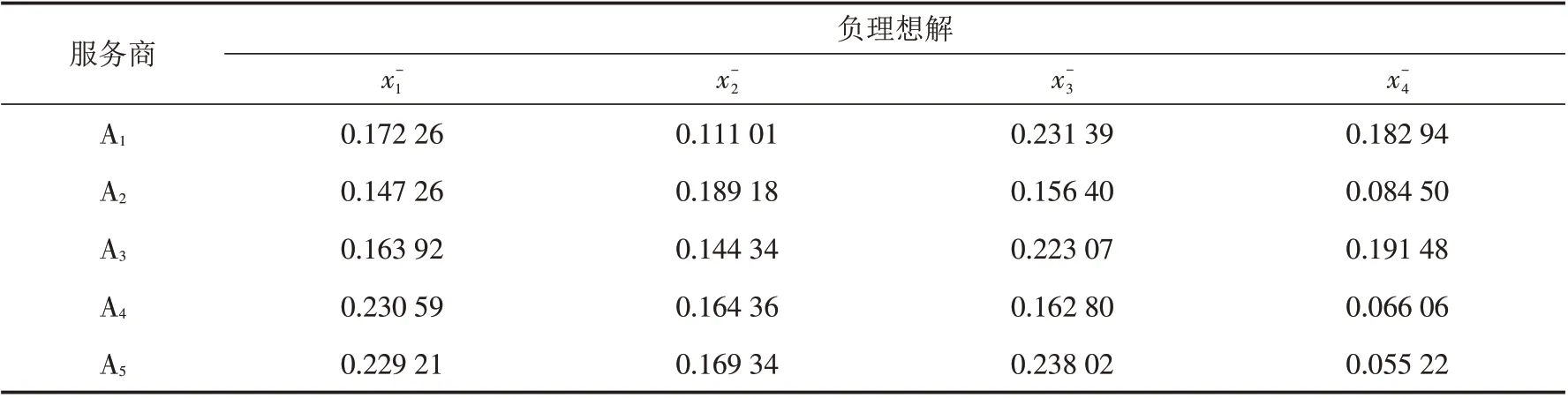
表5 负排序加权距离Tab.5 Negative sort weighted distance

根据步骤6，可以计算出各个方案的贴进度（表6）.

表6 方案贴进度Tab.6 Nearness degree of schemes

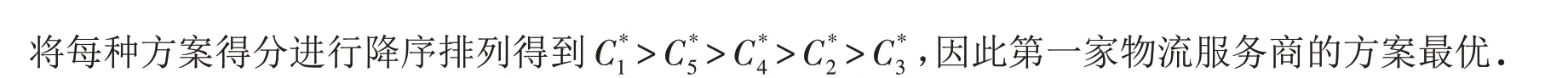
4.3 结果分析

本文中其他4家之所以不是最优的备选服务商原因在于评价标准的权重值不同，C1、C2、C3、C4的权重属性值分别是0.332 7、0.298 9、0.136 9、0.159 1. 第一家物流服务商在运输货物的时间上比较准时，其增值服务能力比较强，送达时间比较短且附加值比较高，熵权法算出评价指标权重值C1和C2比其他两个评价属性值大，第二家的包装设施比较完善，但送达时间比较长且增值服务能力不突出，导致不如第一家物流服务商效率高；第三家和第四家的增值服务能力和顾客满意度比第一家高，但是这两个评价指标的权重值不大，导致不如第一家物流服务商的方案.

综上所述，权重属性值的获取很重要，不能主观赋权，此案例再次验证了运用犹豫模糊TOPSIS方法选择最优物流服务商的可行性和有效性.

5 结论与展望

本文提出了运用犹豫模糊TOPSIS方法选择最优的第三方物流服务商的新方法，首先，采用犹豫模糊理论将专家给出的决策评价的语言形式转化为犹豫模糊数，避免了专家在决策过程中由于犹豫造成的不准确性；其次，利用犹豫模糊熵的方法对属性权重值进行求取，该方法所确定的属性值同时兼顾属性信息的客观情况与决策者的主观意愿，避免了决策信息的单一性；然后，运用加权Hausdorff 距离方法计算正负理想解和5家备选物流服务商之间的距离，与传统的欧式距离相比更加具有客观性及准确性，同时避免了决策者在决策的过程中主观添加隶属度的情况；最后，把犹豫模糊TOPSIS的决策方法运用到真实的选择最优第三方物流服务商的案列中去，为企业选择高质量低成本的第三方物流服务商提供了真实可靠地借鉴方法，评价结果证明了方案的可行性以及客观性. 虽然如此，这种方法依然存在着一些不足之处. 此研究方案是在假设决策者是完全理性的情况下进行的，但是现实情况中人不是完全理性的，如果考虑到人为的主观意愿以及决策者的风险爱好程度，本方案是否具有可行性还有待进一步考量. 除此之外，本文对评价属性的选择数量较少，不能全面覆盖企业的所有特点，评价指标较多的情况下是否依然适用有待以后的进一步研究.