基于改进生物地理学算法的均质土坡滑动面搜索研究
2021-03-22张新启龚爱民徐兴倩罗聪聪
张新启, 龚爱民, 徐兴倩, 罗聪聪, 谢 非
(云南农业大学水利学院,昆明 650201)
边坡安全系数的计算是评价其稳定性的基本依据,极限平衡分析方法仍是边坡防治工程中获取安全系数的主流方法. 其中,瑞典圆弧法具有简单有效,易于编程的优点,被广泛应用于滑面为圆弧形的土质边坡滑动面分析[1]. 采用该方法计算边坡安全系数,最关键的问题是如何从大量可行的计算滑动面中展开精准搜索,并最终确定可靠的边坡临界滑动面. 因此,边坡临界滑面搜索方法的优化研究对于边坡稳定性分析及防治具有重要意义.
目前,主流数值计算软件对圆弧滑面的搜索模块均使用的区格法,如SLIDE、STABL、SLOPE/W(Geostudio)等. 该方法通过n×n点的正方形网格确定临界滑面中心点的位置,计算不同区格点及其半径增量,从而定位安全系数最小的圆弧面[2]. 区格法在边坡圆弧滑动面搜索中应用广泛,求解严格,但该方法搜索范围广、计算量大、受区格划分精度影响不能保证其得到的破坏面就是全局最小值[3]. 因此,搜索空间存在多个局部最小点是定位边坡临界滑面研究的难点问题.
针对此问题,许多学者借助优化算法开展边坡临界滑面的定位研究. 国内外最常用的方法有遗传算法[4-5]、模拟退火算法[6-7]、蚁群算法[8-9]、粒子群算法[10]、鱼群算法[11]等,以上方法均有其各自的优势,但同样也存在些许不足. 例如:遗传算法易于早熟陷入局部最优解,对新空间的探索能力有限;模拟退火算法全局搜索性能受初始值设置影响较大,收敛速度慢;蚁群算法对原始信息素依赖大,容易出现停滞现象.Dan Simon2008 年首次提出生物地理学优化算法(Biogeography-based optimization),是一种利用物种在不同区域内的迁移与突变从而达到平衡的随机优化算法[12],综合了遗传算法与粒子群算法的优点,善于解决高维度非线性问题,但仍存在收敛速度不够快,探索能力有限等局限性.
本文在传统生物地理学算法的基础上提出了一种改进的MBBO(Modified Biogeography-based optimization)算法. 以典型土坡为算例,将瑞典圆弧法中安全系数的计算表达式设定为目标函数,通过在迁移过程中引入随机拓扑结构,实现对边坡临界滑动面的优化搜索. 该方法计算结果与标准生物地理学算法、区格搜索法、遗传算法、粒子群算法相比,其收敛速度快、全局搜索性能更佳.
1 建立目标函数
瑞典圆弧法作为早期的条分法,忽略了土条两侧的作用力,默认破坏面为圆弧形,通过土条整体力矩平衡求解安全系数[13]. 在不考虑孔隙水压力的情况下其计算公式为:式中,ci、φi为第i 块土条的黏聚力与内摩擦角,hi、αi为第i 块土条的平均高度与底面水平倾角,γ 为土条重度,b 为土条宽度.
为保证BBO算法的顺利执行,现以安全系数F为适应度函数,基于圆心点(a,b)及半径R 进行推导. 如图1 所示,假定以圆心O(a,b)与半径R决定的圆弧与边坡的左右交点分别为点A(xout,yout)、B(xin,yin),坡表函数为y=g( x ),将滑动土体分为n个条块,沿X轴正方向对每个土条的中点取值,其坐标分别为Pi(xi,yi),( i=1,2,…,n ). 则有:
基于几何学导出切片底面水平倾角,如图2 所示,可推导出第i 块土条平均长度h 与底面倾角α:

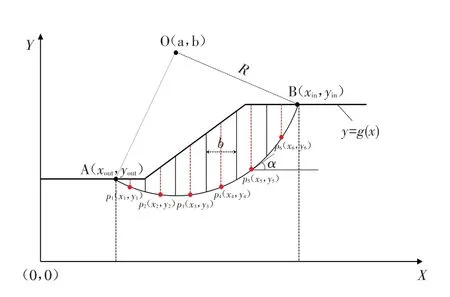
图1 瑞典圆弧法计算模型Fig.1 Swedish arc method calculation model

图2 切片示意图Fig.2 Section diagram
由此,建立了以圆心O坐标与半径R为自变量决定的目标函数,寻优函数可以表示为:

2 BBO算法原理
2.1 基本思路
BBO 算法起源于生物地理学,它通过模拟多物种在不同栖息地的分布、迁移、突变等规律求解寻优问题,在多目标规划领域有广泛应用[14]. 栖息地被认为是独立的区域,不同的栖息地拥有不同的适宜指数HSI(Habitat suitability index). HSI较高的栖息地物种丰富度较高,随着种群趋于饱和,其迁出率增高,迁入率减少,而HIS较低的栖息地与之相反,迁入率增高,迁出率减少. 当栖息地遭遇灾害或瘟疫等突发事件时,HIS将随之突变,打破动态平衡,为低HIS的栖息地添加了不可预见性,增大了搜索目标解的几率.
2.2 迁移和突变操作
物种的迁移有其具体的物理模型,最常的有线性模型、二次模型、余弦模型等. 以图3 线性模型为例,当某栖息地物种数目为0时迁入率最高,此刻λ=I,随着迁入物种数目不断增加,受阳光、水、食物等资源限制,迁入率不断降低,迁出率不断增高. 当栖息地物种数目为S0时,恰好达到动态平衡,此时迁出率与迁入率相同. 而栖息地达到饱和状态时,物种数量达到最大值Smax,此刻不再有物种迁入,迁出率μ=E.
突变操作基于生物地理学统计公式完成:

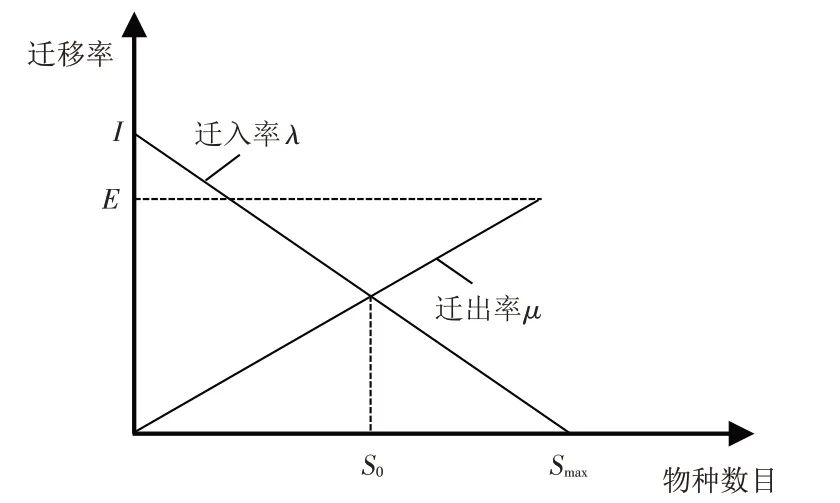
图3 物种迁移模型Fig.3 Species migration model
式中:ms为栖息地发生突变的概率,mmax为最大突变率,用户可自行设定. ps为栖息地容纳s 种物种的概率,pmax代表容纳最大种群的概率.
3 改进的BBO算法
3.1 基于随机结构迁移的MBBO算法
标准的BBO算法使用的是全局拓扑结构,在任意两个栖息地之间均有可能发生迁移操作,如果种群中最优栖息地陷入了局部最优,其信息有较大概率不断迁移给其他栖息地,从而导致算法整体陷入局部最优.
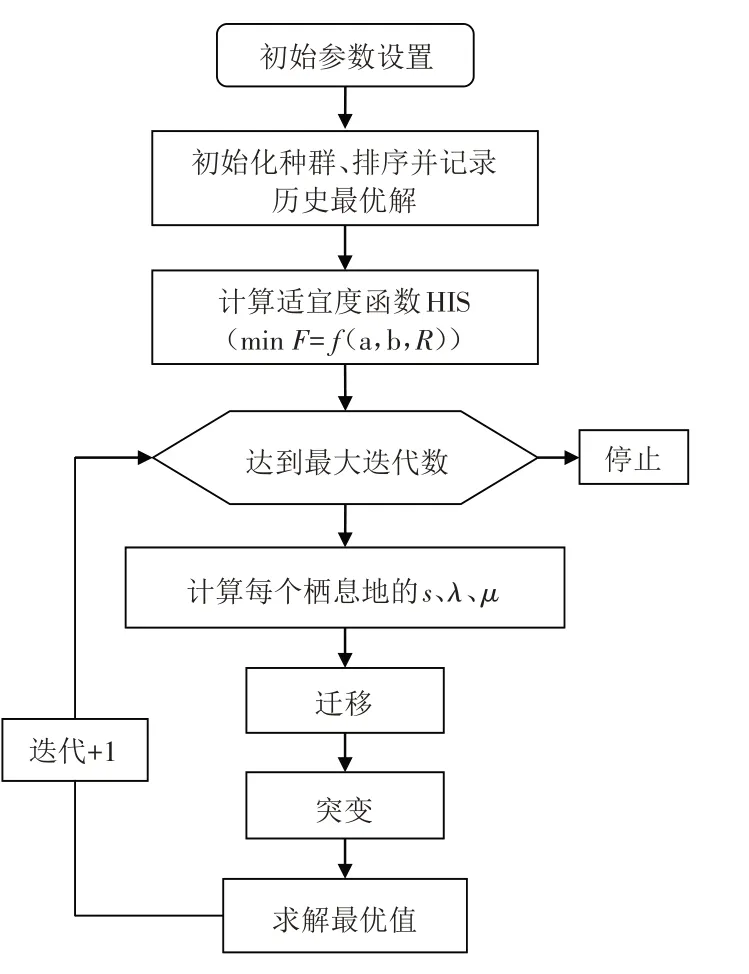
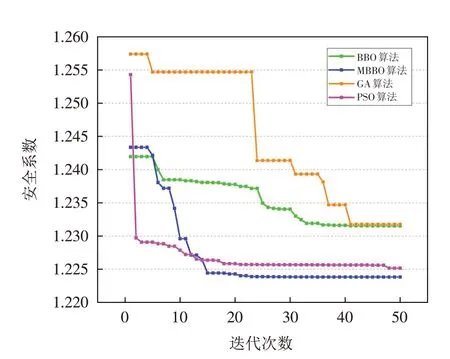
为解决这个问题,本文提出了改进的BBO算法,即MBBO算法. 将随机拓扑结构引入标准BBO算法,可以根据不同需要设置拓扑结构中邻域的平均规模K(0 1)问题参数设置:变量维度及上下界取值; 2)算法参数设置:栖息地数目n、种群最大容量Smax、最大迁入率I/E、最大变异率M; 3)评估给定栖息地的适宜指数HIS:计算该栖息地的种群数、迁出率与迁入率; 4)迁移操作:基于随机拓扑结构得到迁入率λ与迁出率μ,对适宜度向量SIV进行修正,重新计算适宜指数; 5)突变操作:基于突变率更新栖息地种群及适宜指数; 6)采用精英选择策略,继续迭代,直到达到最大迭代次数,如图4所示. 图4 求解流程图Fig.4 Solution flow chart 引用某个坡比为1∶2的典型均质土坡为例[15],该算例的几何模型如图5所示,其力学基本参数为:黏聚力c为9.8 kPa,内摩擦角φ 为10°,容重γ 为17.64 kN/m3,不考虑孔隙水压力影响. 对土坡利用传统的区格法进行分析,采用RocScience Slide软件计算搜索滑弧面. 搜索域由程序给定的正方形组成,网格点数设置为21×21共441个,计算得到的最小安全系数为1.247,搜索得到的土坡临界滑动面如图6所示. 对遗传算法(GA)、粒子群算法(PSO)、生物地理学算法(BBO)、改进的生物地理学算法(MBBO)的搜索性能进行分析比较,在经过连续多次迭代后分别得到各自的收敛值. 寻优曲线如图7所示. 最小安全系数见表1. 图5 均质土坡模型Fig.5 Homogeneous soil slope model 表1 不同算法求解结果对比Tab.1 The results of different algorithms 图6 区格法边坡临界滑面搜索Fig.6 Grid search critical surface 从图7 可以看出,遗传算法与BBO 算法求解的最小安全系数十分相近,求解精度略高于区格法,但两者的收敛速度较慢,相比之下,粒子群算法表现出较好的寻优能力与收敛速度. 改进后的BBO算法在20代左右达到收敛,迭代求解得到的安全系数全局最小,表现出最好的寻优能力,同时收敛速度相比标准BBO 算法显著提高. 各算法迭代过程中用于推导最小安全系数的参数列于表2、3、4、5. 各算法求解得到的圆弧面位置及其圆心点与半径如图8 所示. 从图8 中可以看出,不同算法求解得到的滑面位置均较为接近,侧面反映出圆心搜索域中确实存在有多个局部最小点,而改进的生物地理学算法表现出了最好的优化性能,求解得到的安全系数最小,其相应的临界滑面也最接近于全局最优值. 图7 迭代求解示意图Fig.7 Schematic diagram of optimal curve 表2 MBBO算法在不同迭代次数时求解参数Tab.2 Results for minimum Fos achieved by MBBO over different iterations 表3 BBO算法在不同迭代次数时求解参数Tab.3 Results for minimum Fos achieved by BBO over different iterations 表4 GA算法在不同迭代次数时求解参数Tab.4 Results for minimum Fos achieved by GA over different iterations 表5 PSO算法在不同迭代次数时求解参数Tab.5 Results for minimum Fos achieved by PSO over different iterations 图8 不同方法求得临界滑面示意图Fig.8 Schematic diagram of critical sliding surface is obtained by different methods 1)通过对生物地理学算法的迁移过程引入随机拓扑结构从而提出了一种改进的生物地理学算法,不仅提高了原始BBO算法的全局搜索性能,其迭代时长也有了明显下降. 2)通过对某个典型土坡的安全系数进行求解,与传统的区格法及遗传算法和粒子群算法相比,改进的生物地理学算法寻优能力最好,求解得到的安全系数最低. 3)文中仅对滑面为圆弧形的均质土坡进行了搜索求解. 对于非均质边坡、非圆弧滑面,该算法的求解能力仍需进一步探讨.3.2 MBBO算法计算流程
4 算例分析
4.1 均质土坡模型
4.2 MBBO算法搜索临界滑动面对比分析




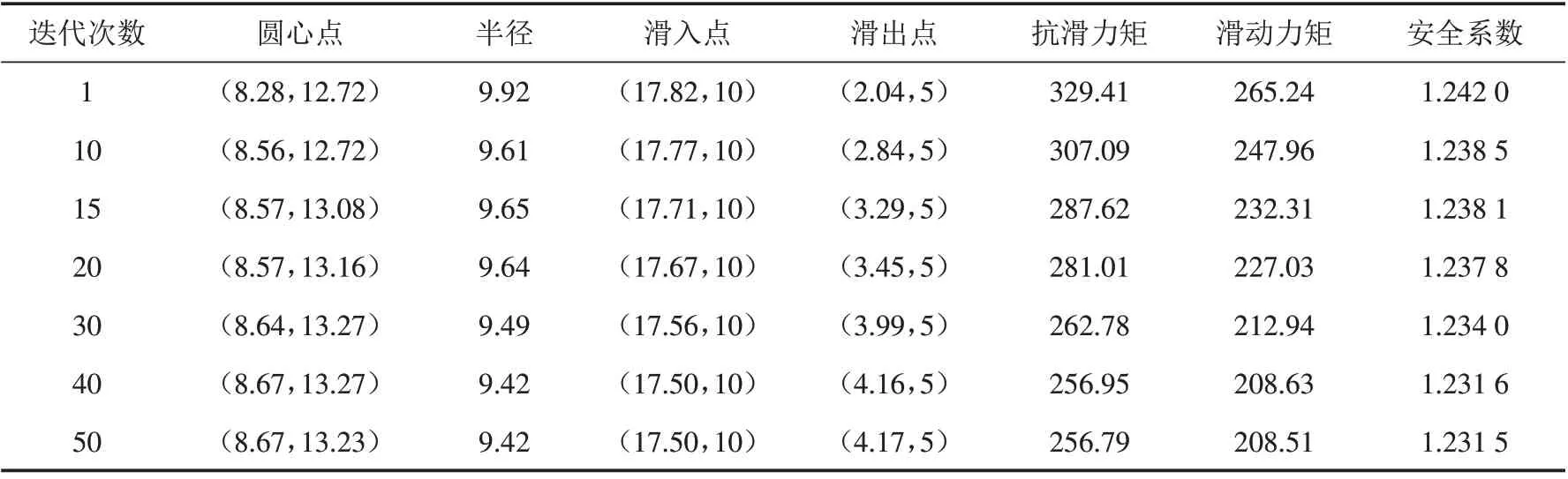


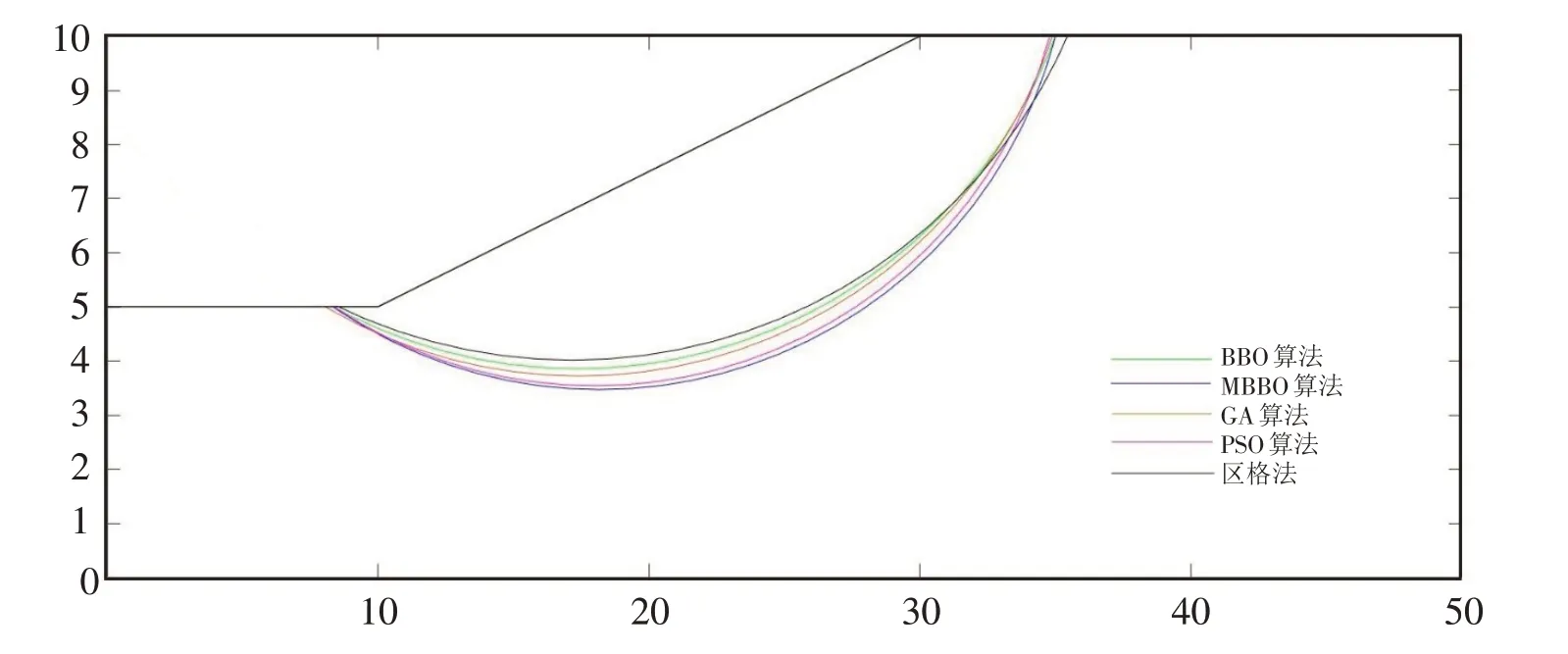
5 结论
