立足教学细节,让课堂教学精彩演绎
2021-03-21张宇蕾

[摘 要] 教学细节是学生知识成长的营养剂,是学生知识发展的基石. 文章以“平行线的性质与判定”专题复习课为例,立足教学细节,以问题情境——问题探究——变式探究的路径展开教学,促使不同的学生在数学上获得不同的发展.
[关键词] 教学细节;精彩演绎;问题;变式;平行线的性质与判定
新课程标准指出,人人要学有价值的数学,不同的人在数学上获得不同的发展. 精彩的课堂是由许多闪光的细节组成的,也是通过细节来演绎的[1]. 如创设一个良好的学习氛围,设置一个有启发意义的情境,教师给予学生一个恰当的评价等. 教学细节是学生知识生长的营养剂,是学生知识发展的基石. 近期,笔者立足教学细节,上了一堂专题复习示范课——“平行线的性质与判定”,现整理出来与大家分享.
“平行线的性质与判定”教学 实录
课前,笔者打开PPT,第一页上显示了课题:平行线的性质与判定;主讲老师姓名:张宇蕾.
师:同学们,你们知道老师姓什么吗?
众生回答:姓张,张老师.
师:既然同学们都认识我了,我也想认识认识大家,谁愿意介绍下自己,并说说自己的兴趣爱好呢?
有几位学生都很自信地介绍了自己,说出了自己的兴趣爱好,然后有一位学生慢吞吞地站起来说:我喜欢打篮球,但是数学不怎么会.
(此时班里有几位学生在偷笑)
师:不会没有关系,到学校来就是要学习不会的东西.
后面又有几位学生介绍了自己,直到上课铃响.
利用课前的几分钟时间,笔者与学生进行了亲切的互动,增进了彼此的了解,与学生进行了情感交流,增进了师生之间的感情.
1. 问题情境
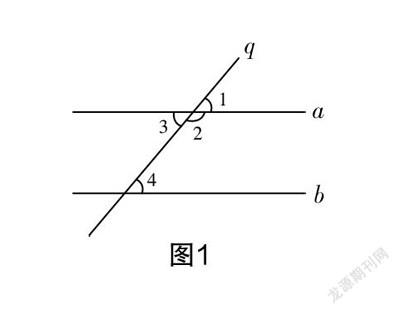
如图1所示,直线q与直线a、b分别相交,你认为图中相等的角有哪些?
创设与实际生活相关的问题情境是多数教师的引入方式,但是笔者一改大多数教师的做法,直接以平行线的具体图形切入课堂,“单刀直入”地引入,能够起到开门见山的作用.
生1:图中可以看到相等的角,包括∠1=∠3,∠1=∠4,∠3=∠4.
师:对于这位同学的回答,同学们有什么异议吗?
生2:图1中并没有给出直线a与直线b是平行关系,所以这些角不一定相等.
然后,教师在黑板板书:当a∥b时,∠1=∠4(两直线平行,同位角相等);当a∥b时,∠3=∠4(两直线平行,内错角相等). 接着笔者提出:对于∠1=∠3,若没有a∥b的条件,还成立吗?
生3:仍然成立,對顶角相等,与直线a、b是否平行没有关系.
师:如果a∥b,那么图1中有哪些互补的角呢?
生4:互补的角有∠2+∠4=180°,∠2+∠3=180°,∠1+∠2=180°,但是∠2+∠3=180°及∠1+∠2=180°与两直线是否平行没有关系.
教师:为什么这么说呢?
生4:根据两直线平行,同旁内角互补,得∠2+∠4=180°;根据邻补角互补,得∠2+∠3=180°,∠1+∠2=180°.
教师继续板书:当a∥b时,∠2+∠4=180°(两直线平行,同旁内角互补).
2. 问题探究
如图2所示,已知直线CD∥EF,点G是平行线外一点,那么∠C,∠E,∠G这三个角之间有何数量关系?并说明理由.
(学生先独立思考,再小组合作交流,教师在教室内巡回指导,与学生互动)
生5:因为CD∥EF,根据两直线平行同位角相等,得∠1=∠E,因为∠1是三角形的一个外角,根据三角形外角的性质,得∠1=∠C+∠G,所以∠C+∠G=∠E.
生6:还可以利用内错角相等来说明. 因为CD∥EF,根据两直线平行内错角相等,得∠2=∠E,因为∠2是三角形的一个外角,根据三角形外角的性质,得∠2=∠C+∠G,所以∠C+∠G=∠E.
生7:还可以利用同旁内角互补进行说明. 因为CD∥EF,根据两直线平行同旁内角互补,得∠3+∠E=180°,根据对顶角相等,得∠3=∠4,根据三角形内角和定理,得∠4+∠C+∠G=180°,所以∠3+∠C+∠G=180°,所以∠C+∠G=∠E.
3. 变式探究
师:针对刚刚提出的问题,同学们回答得很精彩,现在请同学们发挥自己的聪明才智,提出一个问题来考考其他同学.
生8:如图3所示,已知CD∥EF,且∠E=80°,那么∠1的度数是多少?
生9:如图4所示,已知CD∥EF,延长CG得到∠1,且∠C=40°,∠1=160°,求∠E的度数.
两分钟后,没有同学再提出问题.
师:同学们的问题都很有创意!如果去掉“如图”两个字,那么图中点G的位置可能有哪些情况呢?大家可以在练习本上画一画,看能画出几种情况?两分钟后与大家分享.
学生画出了点G可能存在的6种情况,如图5所示.
师:当点G在图5(1)的位置时,如何作辅助线寻找∠C,∠E,∠G这三个角的数量关系呢?
生10:延长DC与GE交于点P.
生11:过点G作GH∥CD
生12:连接CE.
师:三位同学分别从不同的角度解决了同一问题,值得大家借鉴.
“平行线的性质与判定”教学感悟
学生是课堂真正的主人,课堂教学的细节也是从学生的角度展开. 这堂课给学生营造了一种和谐的对话氛围,笔者以自己的行动告诉学生要学会尊重、学会倾听,当学生犯错时,应给予鼓励与引导.
1. 生活细节的情境创设
课前,笔者营造了轻松和谐的课堂氛围,增进了师生关系,也为上课做好了充分的准备. “信其师才能信其道”,当学生说数学不怎么会时,笔者亲切的言语给了学生莫大的鼓舞. 在讲课伊始,笔者设置了一个结论开放的问题,当学生回答出现失误时,让其他学生来纠错,接着给出平行条件,让学生探究互补的角,使其真正成为学习的主人.
2. 委婉巧妙的细节提问
恰到好处的提问可以激发学生的兴趣,启迪学生的智慧,调节课堂氛围[2]. 学生通过笔者巧妙的问题,能够发现自己学习上的不足与优点,从而发扬优点修补缺点. 教育家陶行知曾言:“发明千千万,起点是一问. ”笔者的提问为学生树立了榜样. 尤为值得一提的是,课上笔者让学生自行提出问题,能放能收,当没有学生提问时,及时地从预设中拿出问题,让提问不断充实着课堂.
3. 科学细节的教学评价
在数学课堂教学中,对学生的回答做出恰当的评价,需要教师有良好的素养与教学机智,不仅要做到客观公正,而且要做到评价多样化[3]. 本节课中,对于不同水平的回答,笔者给出的评价也是不同的,有的用语言,有的用手势,有的用眼神,有的用拍肩. 当学生的回答不完整时,笔者耐心地帮助学生一起完成,这样既解决了问题,也保护了学生的自尊心.
参考文献:
[1]黄厚忠,刘新春. 在教学设计细节中体悟“数学味”[J]. 中学数学月刊,2020(12).
[2]孙伟刚. 例谈数学课堂教学细节的缺失与跟进[J]. 云南教育(中学教师),2020(10).
[3]吴小兵. 重视教学细节,彰显教学深度[J].中小学数学(初中版),2020(Z2).
3671501908294
