对数学思维能力培养策略的研究

2021-03-21王细兵

数学教学通讯·初中版 2021年10期

王细兵

[摘要] 学习是习得知识与技能的过程，也是思维成长的过程. 培养学生严谨、周密的数学思维，离不开教师循循善诱的引导. 文章认为思维培养的策略有：情境创设，激活思维;变式训练，启发思维;习题编拟，创新思维.

[关键词] 思维;数学;潜能

随着教育的改革，素質教育的纵深得以有效地发展. 基于新课改背景的初中数学课堂，教师需要更进一步地考虑学生的立场，培养学生的数学思维. 那到底什么样的课堂才能有效地激发学生的潜能，促进学生的思维得以成长呢？文章以课堂教学中的一些环节为着力点，通过一定的教学手段，以引领、启发等方式为学生搭建思维的阶梯.

情境创设，激活思维

乌申斯基曾经说过：“缺乏兴趣的强制性学习，会扼杀掉学习者探究真理的欲望. ”思维能力的培养离不开学生积极的学习态度与对知识的渴求欲. 教师在课堂上创设丰富的教学情境，能形成舒适的课堂氛围，快速吸引学生的注意力，使学生的思维处于兴奋状态[1]. 学生在舒适的课堂氛围与丰富的想象中能产生良好的情感体验，从而激活数学思维，并在情境中经历观察、分析、操作与推理的过程，达到“跳一跳，摘到桃”的成效.

案例1 “三角形内角和定理”的教学.

情境创设：在一个遥远的国度，住着三个大家族——直角三角形、锐角三角形与钝角三角形. 一天，三大家族聚会时三大家族的法老因一件事情吵了起来. 直角三角形家族的法老说：“我们家族的个子最高，所以我们家族的内角和最大. ”钝角三角形家族的法老说：“我们家族有一个角比你们任何家族的角都大，因此我们家族的内角和才是最大的. ”锐角三角形家族的法老说：“不不不，我们家族成员的面积大，因此我们家族的内角和比你们都大. ”为此，三大家族的法老争得面红耳赤，谁也不服输. 聪明的你觉得哪个家族的内角和最大呢？

学生听了这个故事，面面相觑，觉得每个法老说得都有道理，瞬间就对三角形的内角和产生了探索的欲望.

生1：可以画三种类型的三角形，用量角器测量各个角的度数，再将每种三角形三个角的度数加起来.

师：这个方法不错，简单易行. 假设在那个国度没有量角器该怎么办呢？

（学生陷入沉思）

生2：可以剪三种类型的三角形各一个，然后将每种三角形的三个角剪下来，拼接在一起，最后比较拼接完成后的角度的大小.

师：这是个好方法！说干就干，我们现在就来操作吧，为这三位法老找出正确答案.

（学生兴奋地画图、撕图、撕角、拼角）

生3：我们发现，三种类型的三角形的内角和竟然都是180°.

……

上述教学片段用学生感兴趣的童话故事引出问题，并将三类三角形都囊括到故事情境中. 学生在兴趣的驱使下积极开动脑筋，想方设法地为法老们出主意，探寻问题的答案. 最后，他们决定以实际操作来解决这一问题，于是自然而然地便将问题情境转化为了问题探究. 整个过程衔接自然，不仅激活了学生的思维，还培养了学生的动手操作能力，为学生数学核心素养的提升做了铺垫.

变式训练，启发思维

“穷则变，变则通. ”学习亦如此. 一味地埋头苦干，并不一定能获得较好的成效. 有时候，我们需要打破常规思维，从不同的视角去审视、观察与分析问题，这样反而能“柳暗花明又一村”. 因此，光说不练不行，光练不总结也不行. 教学中，教师应培养学生思维的灵敏性，通过一些经典例题的引申，让学生达到做一题，会一类题的能力[2].

变式训练作为启发学生思维的利器，能让学生在万变不离其宗的变式中感受数学独有的魅力. 所谓变式，是对试题的题设条件或结论进行改变. 解题时，学生只要紧扣问题的核心，学会从不同层次、不同角度去观察与反思问题，就能深化对问题的理解，从而形成较强的数学思维能力.

案例2 “角平分线”的教学.

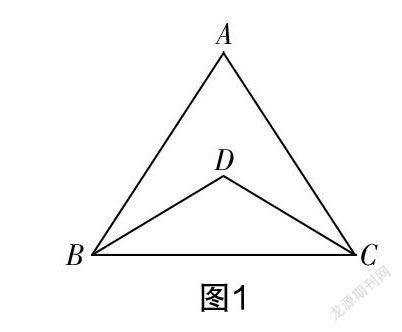
原题如图1，在△ABC中，∠ABC与∠ACB的平分线相交于点D，猜想∠A与∠BDC之间的数量关系，并说明理由.

为了深化学生对这一知识的理解，教师可在此题的基础上进行适当变化，利用变式训练来启发学生思维.

变式1 如图2，在△ABC中，∠ABC与∠ACB的外角平分线相交于点D，猜想∠A与∠BDC之间的数量关系，并说明理由.

变式2 如图3，在△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于点D，猜想∠A与∠BDC之间的数量关系，并说明理由.

上述过程以原题为模板，对其进行变式，能加深学生对该部分知识的理解，从而达到灵活运用的目的. 可见，变式训练不仅能启发学生的思维，还能让学生感受到数学的神奇，从而开阔学生的视野，提高学生解决问题的能力.

习题编拟，创新思维

学与思有着密不可分的联系，处理好学与思之间的关系，是实现有效教学的关键. 要培养学生的数学思维，凭借单纯的知识传授远远不够，学生思维的培养与创新能力的提升还离不开对各种学习技能的掌握. 教师应鼓励学生编拟试题，让学生充分发挥自己的主观能动性，在对知识的剖析与深思中激活思维，在编拟试题的过程中实现思维创新.

此外，学生在编拟试题时受知识面与思维能力的影响，难免会出现考虑不周的情况. 此时，教师可从学生所编试题的错误中发现学生知识的漏洞，以及思维的不严谨之处，从而对其进行针对性指导. 编拟试题，能让学生提升数学能力，完善知识结构，并使思维更加严谨.

案例3 “应用题”的复习教学.

复习“应用题”时，笔者设计了这样一道题：已知立体贺卡3元/张，平面贺卡2元/张. 请同学们添加一定的情境和数据，让其成为一道完整的数学试题，并完成解答.

生1：李红准备去书店购买12张贺卡，已知立体贺卡3元/张，平面贺卡2元/张，她付了30元，找回7元. 李红购买了多少张立体贺卡？

师：大家觉得这么编行不行？为什么？

生2：我觉得不好. 题目没有交代清楚是购买一种贺卡还是两种，如果只购买了立体贺卡，那么价格就不对，因为23不是3的倍数;如果购买了两种贺卡，答案就有多种可能. 因此，在表述问题时，需要做到清晰.

师：生2分析得非常好！哪位同学来加点新的条件呢？

生3：小丽准备在家搞一个新年晚会，她去超市购买贺卡. 已知立体贺卡3元/张，平面贺卡2元/张，两种贺卡一共准备购买10张，总价格控制在25元以内，该怎么购买？

师：谁来分析一下这位同学编拟的题目？

生4：小丽在自己家搞新年晚会，一般是来参加晚会的同学送贺卡给她，而不是她自己去购买贺卡.

师：有道理. 那怎么说比较合理？

生5：小丽准备在家搞一个新年晚会，她的10位朋友准备一起到超市购买贺卡，计划每人购买1张. 已知立体贺卡3元/张，平面贺卡2元/张，怎样购买，能使总价控制在25元以内？