三角形排列折边式蜂窝夹套结构强度影响因素分析
2021-03-20
(南京工业大学 机械与动力工程学院,江苏 南京 211816)
夹套是反应容器的重要组成部分,一般设置在容器的筒体或封头外侧,使用焊接或法兰方式与筒体连接后,筒体和夹套间就形成了一个密封空间。蜂窝夹套是一种新型夹套形式[1],是以整体夹套为基础,将内筒体与蜂窝底部的小圆孔焊接在一起,构成蜂窝结构。一般采取折边或短管等加强措施,来提高内筒体的刚度和蜂窝夹套的承载能力,减少流道面积,从而适当减薄筒体厚度。其传热效果比其他夹套结构显著[2-3],成本相对较低,但加工要求高,自20世纪90年代开始被广泛应用于工业生产中。
文中对三角形排列方式的折边式蜂窝夹套结构强度影响因素进行分析,采用正交试验[4-5]进行数值模拟方案设计,使用极差和方差分析方法,分析不同结构尺寸参数对蜂窝夹套强度[6-7]的影响显著性,最后利用响应面分析法[8],拟合得到了不同结构尺寸参数的蜂窝夹套应力多元回归方程[9]。
1 蜂窝夹套结构尺寸及设计参数
采用如图1a所示的三角形排列折边式蜂窝夹套容器简化模型,研究分析不同蜂窝尺寸参数对蜂窝夹套结构强度影响的显著规律。蜂窝夹套结构及参数见图1b。
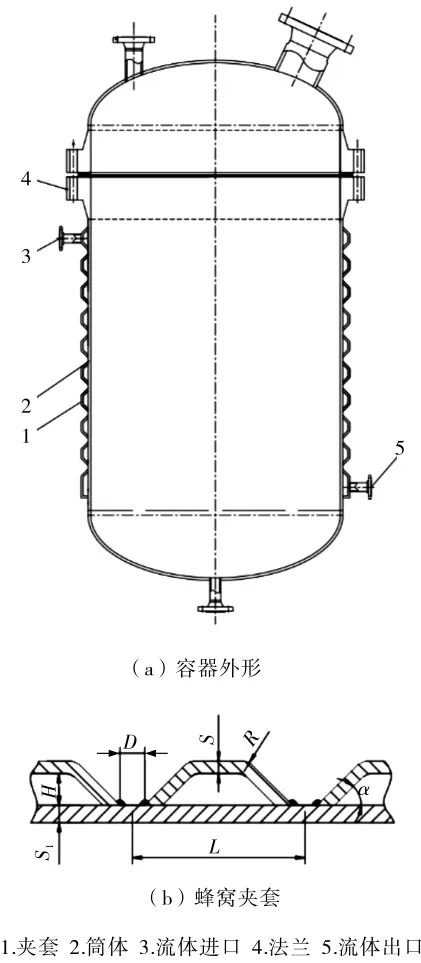
图1 折边式蜂窝夹套容器结构示图
该蜂窝夹套容器的筒体内直径为1 300 mm,高度1 515 mm,筒体厚度 S1=14 mm;夹套内直径1 380 mm,高度1 410 mm。蜂窝轴向间距L=140 mm、蜂窝圆孔直径D=20 mm、蜂窝厚度S=10 mm、蜂窝高度H=26 mm、蜂窝拐角半径 R=8 mm、蜂窝锥度α=45°。
蜂窝夹套容器的主要设计参数见表1。

表1 蜂窝夹套容器主要设计参数
2 蜂窝夹套正交试验方案设计及仿真模拟结果
2.1 正交试验设计
正交试验设计是研究多个因素和多个水平的常见设计方法,通过选用恰当的正交试验表进行分析,从而寻找出最优的自变量组合方式。
正交试验设计是一种高效、快速、经济的试验设计方法。文中选用5个因素,即蜂窝轴向间距L、蜂窝圆孔直径D、蜂窝厚度S、蜂窝高度H以及蜂窝拐角半径R,每个因素选取5个水平,见表2。
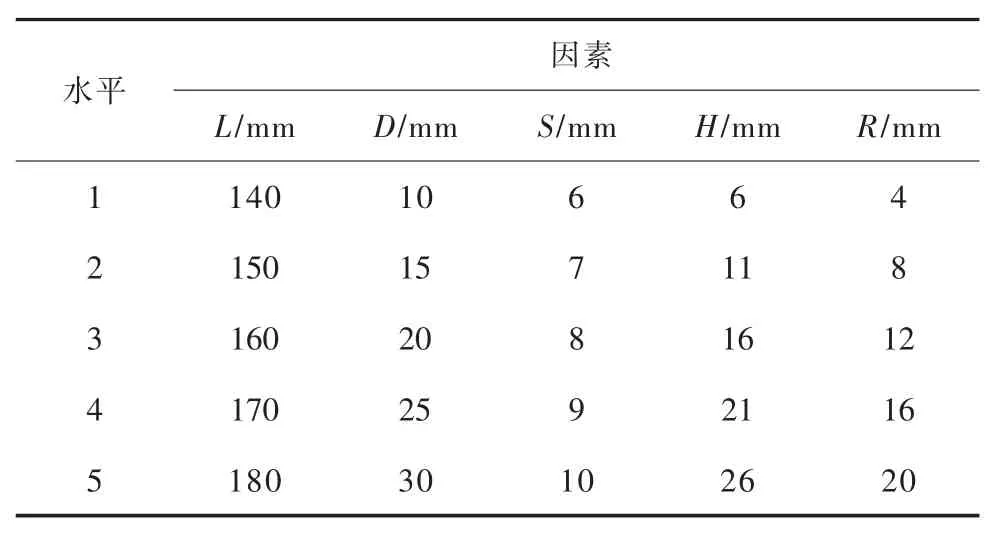
表2 蜂窝夹套正交试验水平及因素选取
2.2 试验方案与仿真结果
采用ANSYS软件对折边式蜂窝夹套进行参数化建模并进行应力分析[10],根据应力分析结果在最大危险点所在位置进行线性化路径处理[11-12],从而获得蜂窝夹套的一次局部薄膜应力PL以及一次加二次应力PL+Pb+Q。正交试验方案和仿真模拟结果见表3,表中的误差列系为残差分析准备。
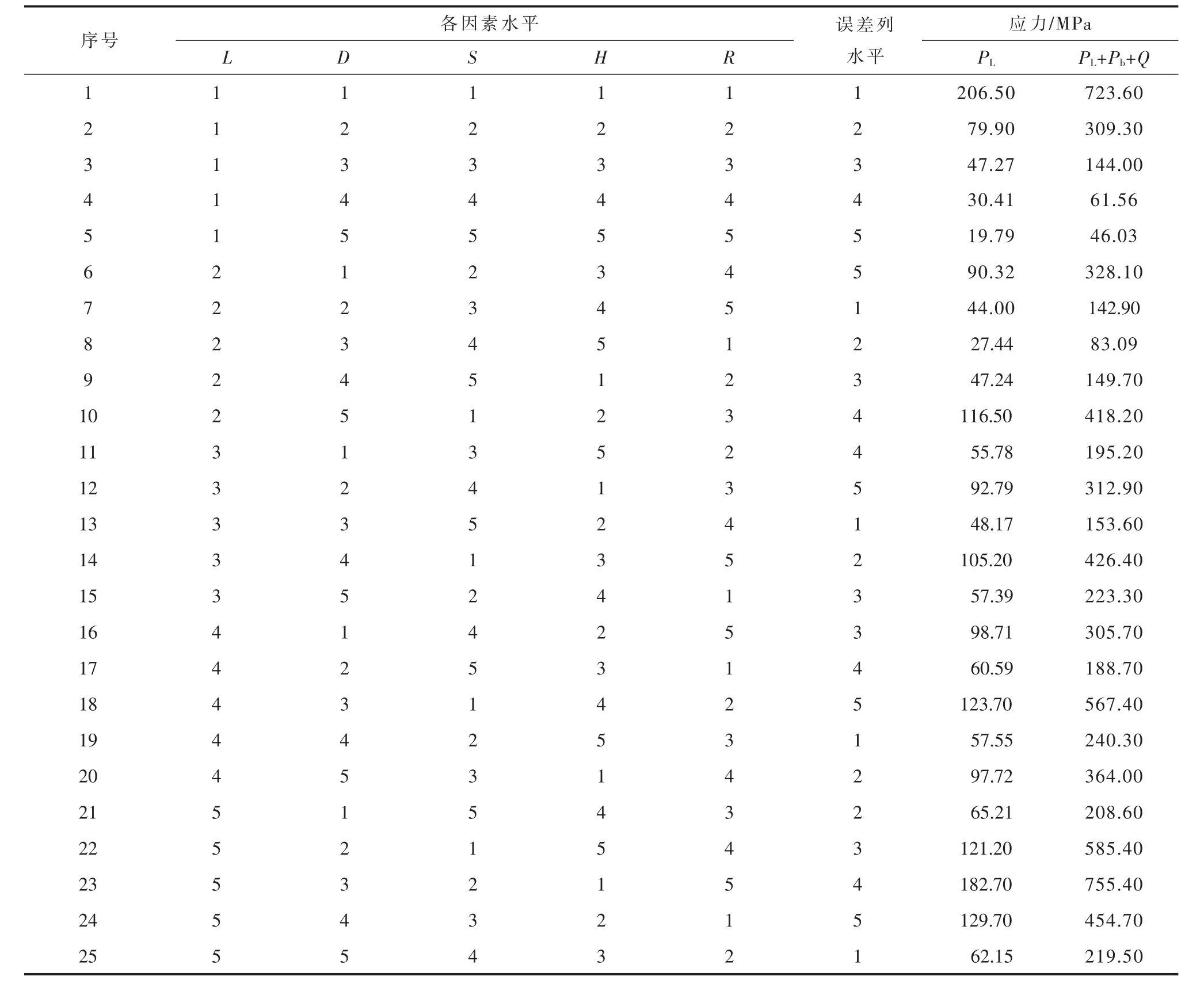
表3 蜂窝夹套应力正交试验方案和仿真模拟结果
3 蜂窝夹套正交试验数据分析
3.1 极差分析
极差分析法又称直观分析法,其直观形象、操作简单、对数据处理较为简便,是最常用的一种数据处理手段[13-17]。采用极差分析法对正交试验得到的蜂窝夹套一次局部薄膜应力和一次加二次应力数据进行极差分析,结果见表4和表5。

表4 蜂窝夹套一次局部薄膜应力极差分析结果 MPa
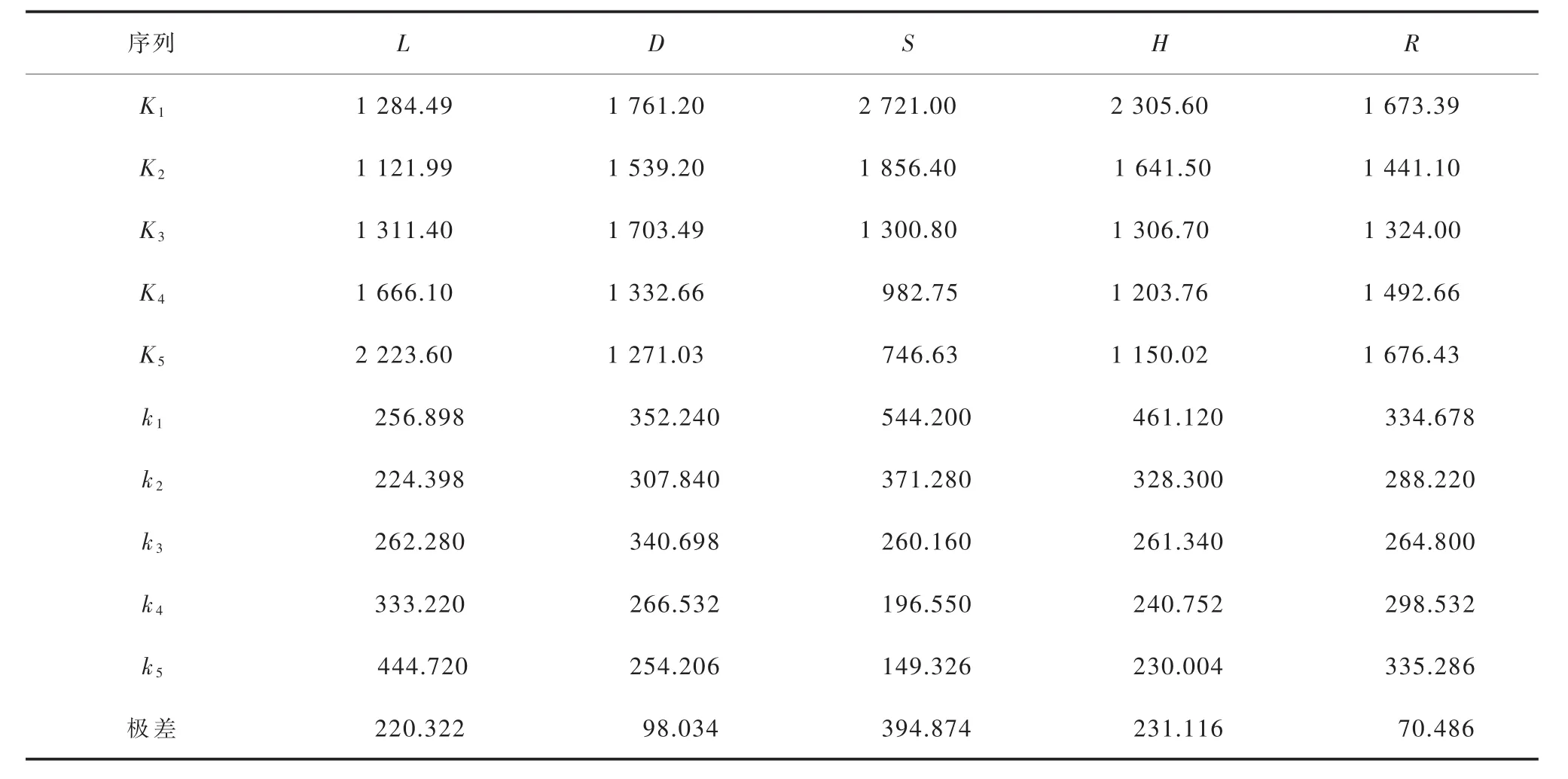
表5 蜂窝夹套一次加二次应力极差分析结果 MPa
表 4 和表 5 中, 与 L、D、S、H、R 对应的 K1、K2、K3、K4、K5分别依次为表 3 中各自的 5 个一次局部薄膜应力或一次加二次应力 (分别对应序号1~5、6~10、11~15、16~20、21~25) 相加所得的数值,k1(k1=K1/5)、k2(k2=K2/5)、k3(k3=K3/5)、k4(k4=K4/5)、k5(k5=K5/5)中最大值与最小值之差为极差。 K1、K2、K3、K4、K5分别代表不同水平所对应一次局部薄膜应力或一次加二次应力的总值,k1、k2、k3、k4、k5分别代表不同水平相对应一次局部薄膜应力或一次加二次应力的平均值。极差越大,对结果的影响越大。
从表4和表5可以看出,因素S极差最大,表明在改变水平时,因素S对蜂窝夹套一次局部薄膜应力或一次加二次应力的影响最大;因素R的极差最小,表明在改变水平时,因素R对蜂窝夹套一次局部薄膜应力或一次加二次应力的影响最小。
根据表 4 和表 5 中 k1、k2、k3、k4、k5数值所对应的极差值,做出各因素水平对蜂窝夹套一次局部薄膜应力和一次加二次应力的影响趋势曲线,见图2和图3。
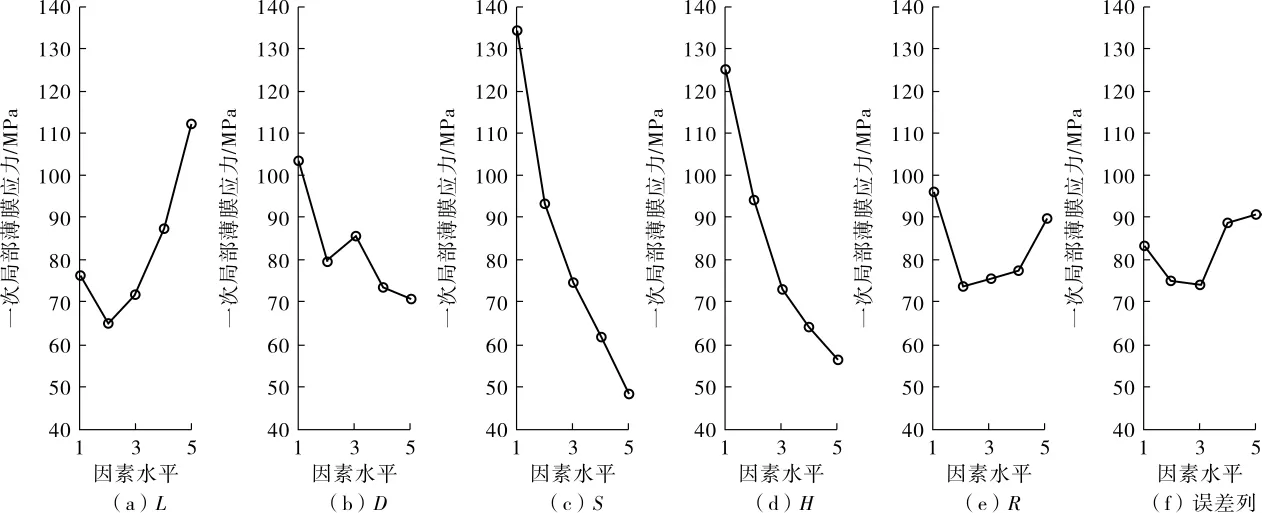
图2 各因素水平对蜂窝夹套一次局部薄膜应力影响趋势图
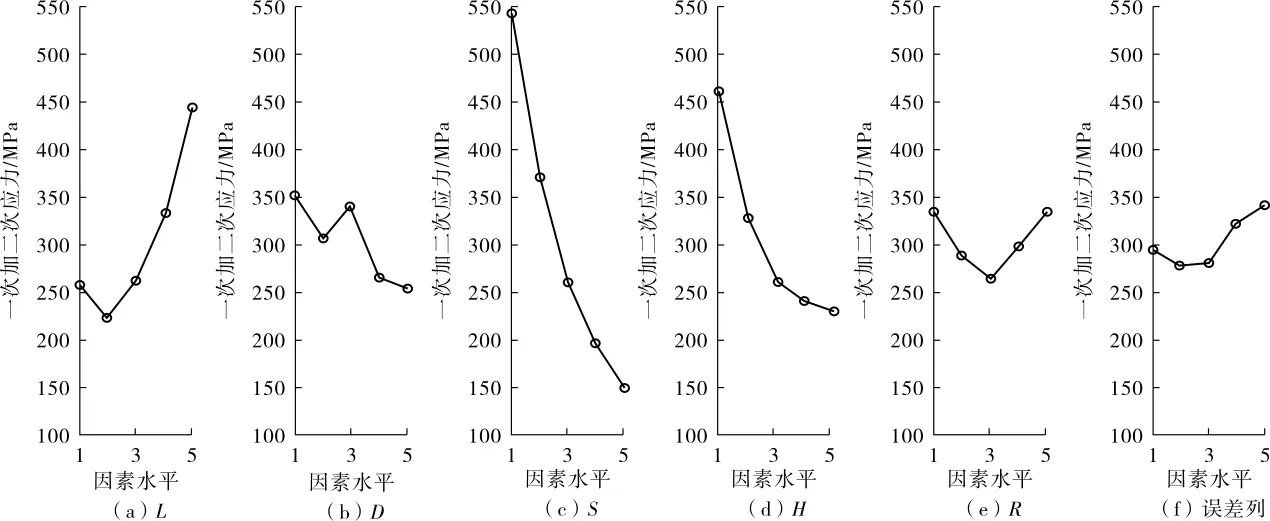
图3 各因素水平对蜂窝夹套一次加二次应力影响趋势图
由图2可知,因素S在水平5时所对应的应力最小,因素R在水平2时所对应的应力最小。结合表2、表3分析可知,各因素水平对蜂窝夹套一次局部薄膜应力影响的最优方案依次为S5、H5、L2、D5、R2。同理,由图 3 结合表 3 的分析,可得各因素水平对蜂窝夹套一次加二次应力影响最佳方案依次为 S5、H5、L2、D5、R3。
3.2 方差分析
由于极差分析不能辨别是由试验误差引起的数据波动,还是由试验条件引起的数据波动,因此无法确定试验的精度。为了弥补极差分析法的不足,可采用方差分析法进行分析[18-22]。根据表1和表2中的数据,得到蜂窝夹套一次局部薄膜应力和一次加二次应力的方差分析结果,见表6和表7。表中SS为总偏差平方,df为自由度,MS为方差,F为统计量,p为概率。
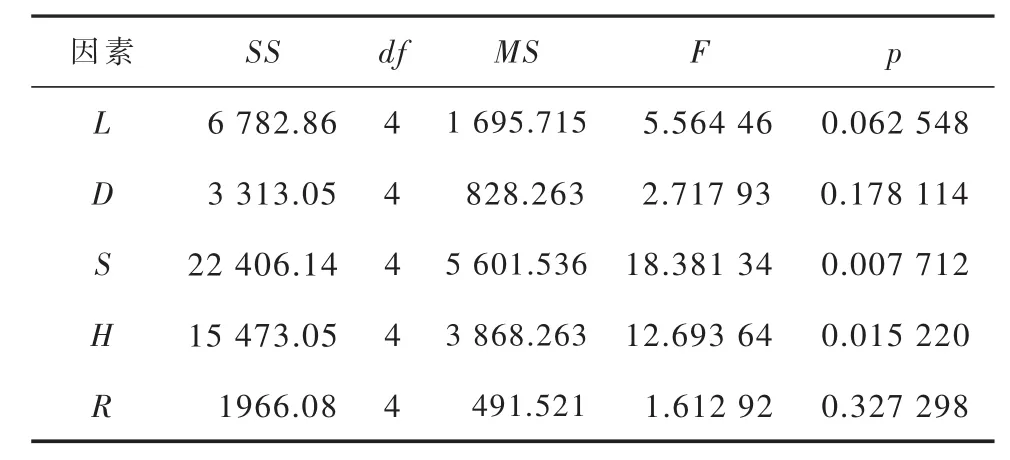
表6 蜂窝夹套一次局部薄膜应力方差分析结果
由表6可以看出,蜂窝厚度S、蜂窝高度H的概率值p均小于0.05,表明两者对蜂窝夹套一次局部薄膜应力影响是统计显著的,各因素显著性从大到小排列为 S、H、L、D、R。 由表 7看出,蜂窝壁厚S、蜂窝高度H、蜂窝轴向间距L的概率值p均小于0.05,表明此3个因素对蜂窝夹套一次加二次应力的影响是统计显著的,各因素显著性从大到小排列为 S、H、L、D、R。
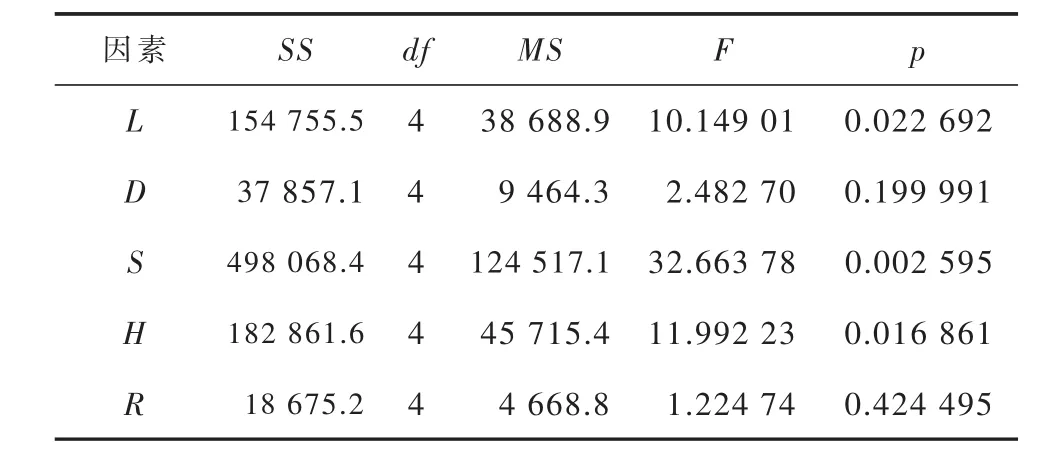
表7 蜂窝夹套一次加二次应力方差分析结果
由极差分析和方差分析结果可以看出,影响蜂窝夹套一次局部薄膜应力和一次加二次应力的显著因素依次均为 S、H、L、D、R, 两者具有相关性。因此,在工程设计时,如果仅从经济性但又不影响结构强度的角度考虑,可以采用保证蜂窝厚度不变,适当增加蜂窝高度和适当减小蜂窝轴向间距的办法实现。
4 蜂窝夹套应力响应面分析
4.1 方案设计
从极差分析和方差分析可以知道,蜂窝壁厚S、蜂窝高度H、蜂窝轴向间距L对蜂窝夹套应力的影响相对显著,而蜂窝圆孔直径D、蜂窝拐角半径角R对结构应力的影响显著性不明显。为了解S、H、L三者之间对蜂窝夹套应力的影响关系,笔者利用响应面分析法,采用Design-Expert软件的 Box-Behnken Design模型[23]设计响应面试验。选取自变量S、H、L为参数,设置一次局部薄膜应力及一次加二次应力为响应值。响应面分析选用的中心组合试验的因素及水平见表8。

表8 蜂窝夹套响应面分析法中心组合试验因素及水平
根据Box-Behnken设计原理,设计3因素3水平共17组响应面分析试验,结果见表9。
4.2 响应面分析
4.2.1 一次局部薄膜应力
利用Box-Behnken响应曲面对表9试验数据进行多元回归拟合,得到蜂窝夹套一次局部薄膜应力的二次多项回归方程为:

表9 蜂窝夹套响应面分析法中心组合试验方案设计及试验结果

对蜂窝夹套一次局部薄膜应力的二次多项回归方程进行方差分析,结果见表10和表11。
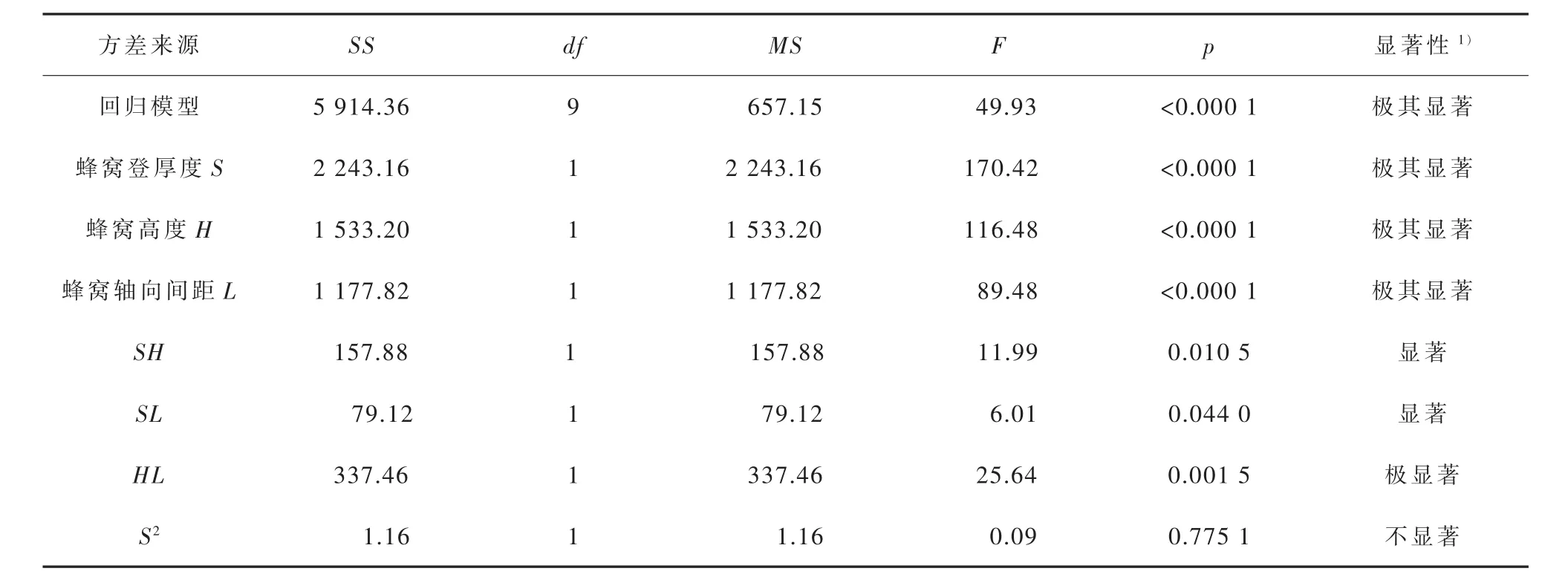
表10 蜂窝夹套一次局部薄膜应力的二次多项回归方程方差分析结果
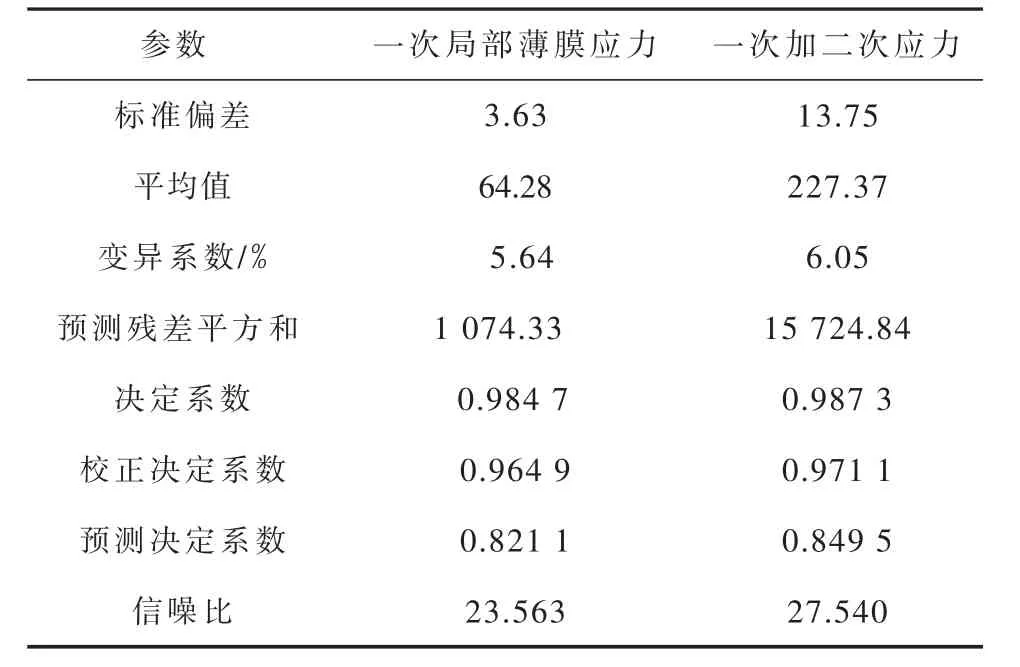
表11 蜂窝夹套应力二次响应回归模型方差分析参数
由表10可知,一次项蜂窝厚度S、蜂窝高度H、蜂窝轴向间距L对蜂窝夹套一次局部薄膜应力的影响为极其显著,交互项HL的影响为极显著,交互项SH、SL的影响为显著,回归模型的影响也是极其显著,说明该二次多项回归模型对于蜂窝夹套一次局部薄膜应力的分析和预测较为准确。模拟失拟度为0.151 4>0.05,代表失拟项不显著,所以能够使用该回归方程模拟试验数值。
由表11可知,式(1)模型回归方程的决定系数为0.984 7,表明该回归模型的拟合度较好,试验误差小,有着较高的可信度。变异系数为5.64%<10%,进一步说明该模型具有较高的稳定性,拟合度较好。
4.2.2 一次加二次应力
同理,依据表9试验数据拟合得到蜂窝夹套一次加二次应力的多元二次回归方程为:

对蜂窝夹套一次加二次应力的二次多项回归方程进行方差分析,结果见表11和表12。
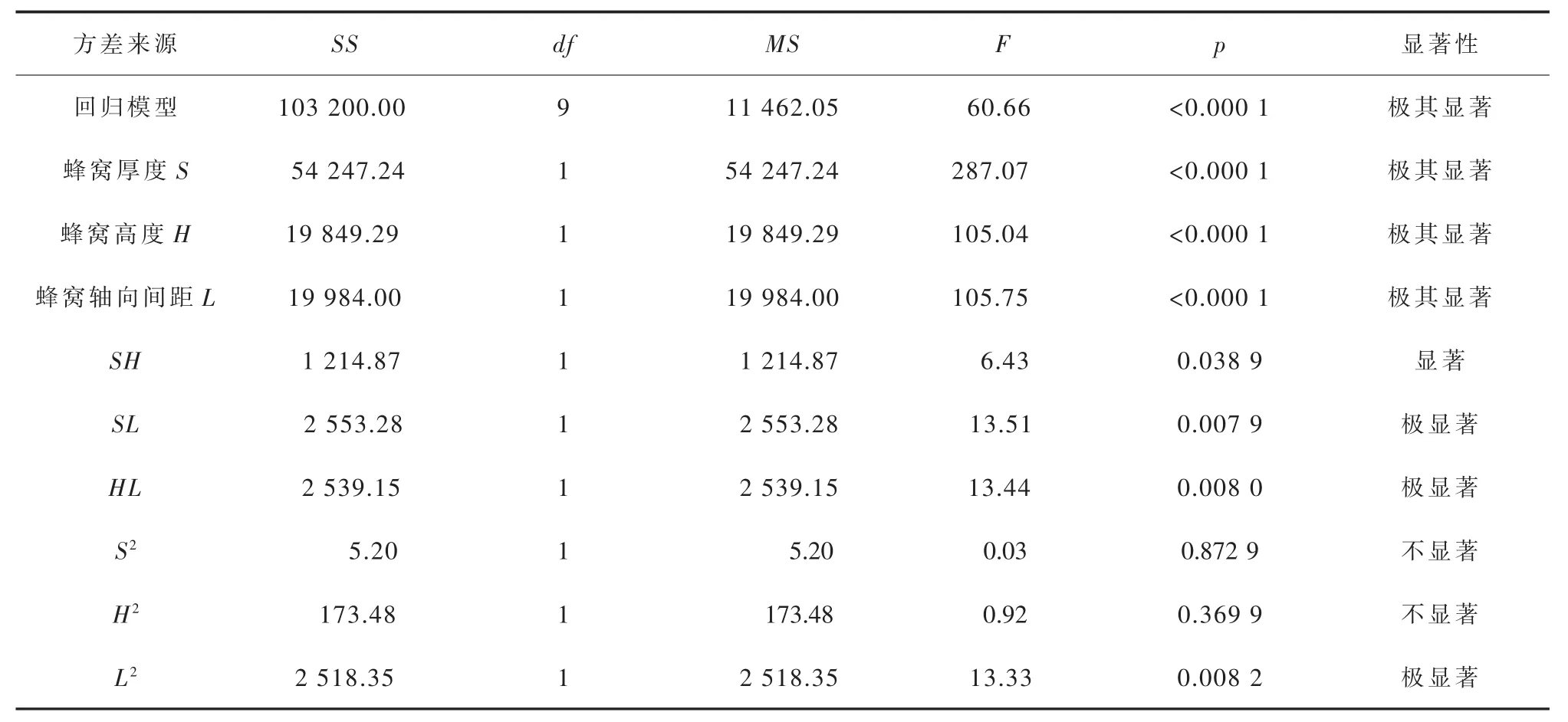
表12 蜂窝夹套一次加二次应力的二次多项回归方程方差分析结果
综合分析表11和表12的数据可以知道,用式 (2)模型来表示各因素和响应值的函数关系具有相当的可靠性,模型的稳定性较高,拟合度较好。
4.3 回归模型准确性验证
蜂窝夹套应力回归模型预测值与实际值的差值为残差。一般情况下,正常的残差必须是正态分布的。蜂窝夹套应力回归模型残差正态概率分布见图4和图5,应力预测值和实际值分布见图 6和 7。其中,预测值由式(1)和式(2)得到,实际值由试验结果得到,残差是预测值与实际值之差。
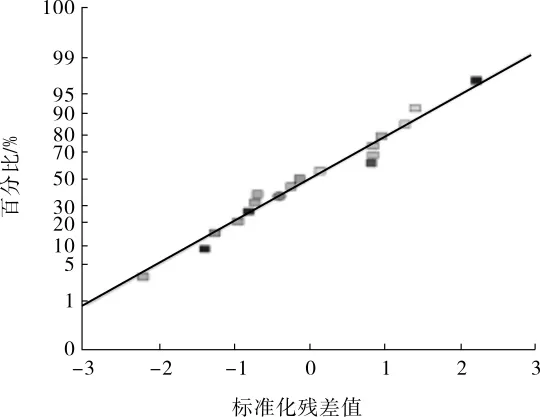
图4 蜂窝夹套应力回归模型一次局部薄膜应力残差正态概率分布

图5 蜂窝夹套应力回归模型一次加二次应力残差正态概率分布
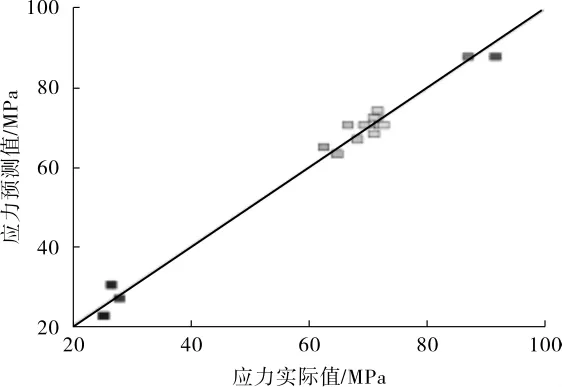
图6 蜂窝夹套应力回归模型一次局部薄膜应力预测值和实际值分布情况
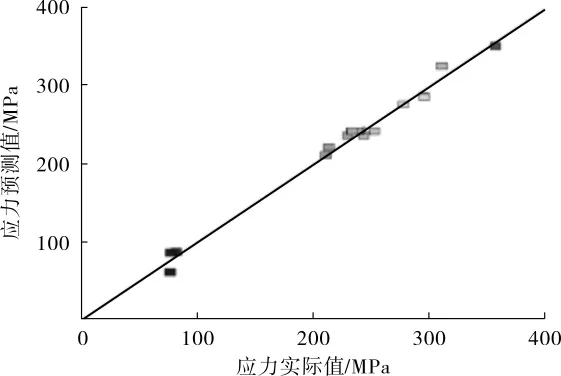
图7 蜂窝夹套应力回归模型一次加二次应力预测值和实际值分布情况
由图4和图5可知,各个应力残差散点均在同一条直线上或在其附近分布,表明本次研究的蜂窝夹套应力残差是正态分布,进一步说明了该响应面拟合模型的可行性。蜂窝夹套应力预测值以及实际值的分布规律(图6和图7)与应力残差分布相类似,各个散点均在同一条直线上或在其附近排列,说明应力预测值和实际值误差很小,该模型可靠,可以用作预测试验模型。
4.4 等高线图及3D响应面图分析
为了直观观察各因素之间的相互作用对蜂窝夹套应力的影响,通过固定蜂窝厚度S、蜂窝高度H、蜂窝轴向间距L其中任意一个因素,绘制其他2个因素相互影响的等高线图以及3D响应面图。如果等高线图大致为椭圆形,相互作用是显著的;若等高线图为圆形,相互作用是不显著的。等高线间距越密集,说明因素之间的相互作用越显著。3D响应面图的倾斜度越高,说明因素之间的相互作用越显著。
各因素相互作用对蜂窝夹套一次局部薄膜应力影响的等高线图见图8,3D响应面图见图9。
由图8和图9可以知道,因素S和H、S和L、H和L的相互作用均对蜂窝夹套的一次局部薄膜应力影响显著,与表10中方差分析得到的结果是一致的。

图8 各因素相互作用对蜂窝夹套一次局部薄膜应力影响的等高线图

图9 各因素相互作用对蜂窝夹套一次局部薄膜应力影响的3D响应面图
各因素相互作用对一次加二次应力影响的等高线图见图10,3D响应面图见图11。
由图10和图11可知,因素S和H、H和L以及S和L的相互作用均对蜂窝夹套的一次加二次应力影响显著,也与表12中方差分析得到的结果相应一致。
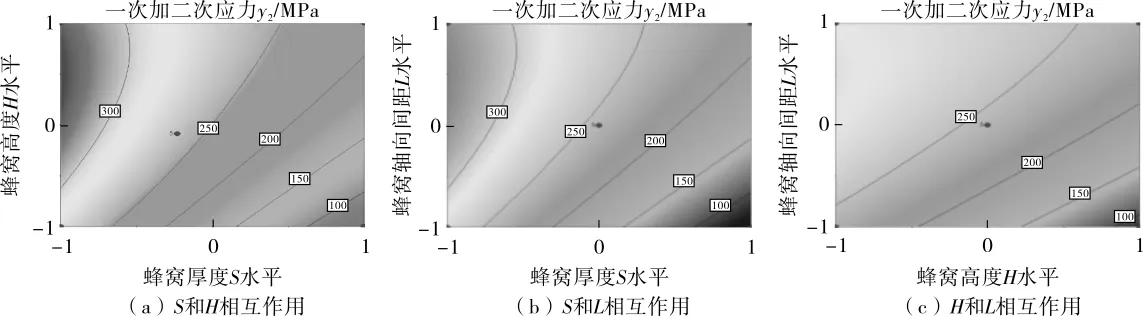
图10 各因素相互作用对蜂窝夹套一次加二次应力影响的等高线图
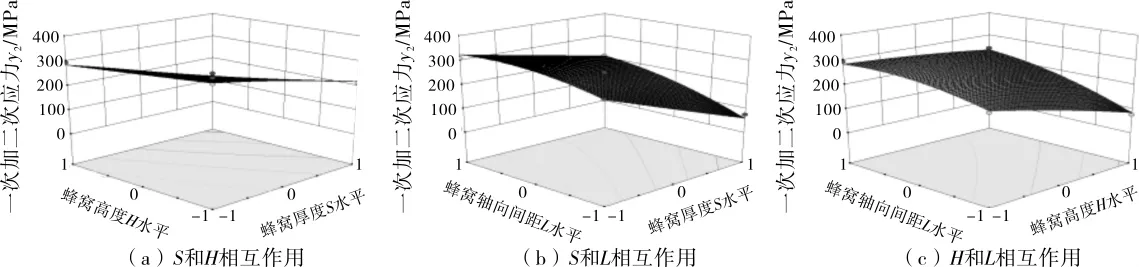
图11 各因素相互作用对蜂窝夹套一次加二次应力影响的3D响应面图
5 结语
采用ANSYS参数化建模功能,对三角形排列方式的折边式蜂窝夹套进行多组不同尺寸参数试验模拟,利用正交试验中的极差和方差分析法研究各结构参数对蜂窝夹套一次局部薄膜应力和一次加二次应力的显著影响水平,并采用响应面法拟合得到了不同结构参数的蜂窝夹套应力多元二次回归方程。分析研究表明,影响折边式蜂窝夹套一次局部薄膜应力及一次加二次应力的因素显著性从大到小均为 S、H、L、D、R,表明影响折边式蜂窝夹套应力强度的显著性因素依次为S、H、L、D、R。在工程设计中,如果仅从经济性但又不影响结构强度的角度考虑,可以采用保证蜂窝壁厚不变,适当增加蜂窝高度和适当减小蜂窝轴向间距的办法来改善应力水平。
