基于马氏距离相关性的PLS变量选择与应用*

周昭君，韦程东，陈丽玲，林玉婷

(南宁师范大学 数学与统计学院，广西 南宁 530100)

1 引言

由于信息技术的快速发展及其在科学实验、生产和日常生活中的广泛应用，在众多领域中人们有大量复杂的高维数据集亟待分析，比如代谢组学数据、基因微阵数据、质谱数据和光谱数据等等.这些数据普遍具有高维度、高噪声、高冗余且分布未知等特点，因而，传统的统计学方法已经不再能够处理这类数据.对此，研究人员发展了许多新的统计算法和理论，用于对高维数据进行分析.其中模型的变量选择方法是一种有效处理高维数据的方法，它主要通过选择“有效信息变量”来建立“最优的模型”，不仅能提升模型的预测和解释能力，还能提高计算效率.

近年来，最具代表性的变量选择方法是基于惩罚的变量选择法和基于相关性的变量选择法，两类方法都在只有部分解释变量作用于响应变量的稀疏假设下适用. 惩罚类型的变量选择法主要思想为针对添加了关于模型复杂度的惩罚函数的极大似然函数或最小二乘函数，计算模型最值以获取参数的最优估计.此类方法最早体现在Mallows[1]提出的Cp准则上，该准则采用最小二乘为假设的线性回归模型优良性进行评估，适用于方差已知且基于平方损失的线性模型；对于方差未知的情况，赤池准则提出AIC指标对变量个数施加惩罚，与Cp准则有着等效的作用，适用于更多的模型；后来Schwarz提出的BIC准则对样本量也施加了惩罚，但其模型相对于AIC准则更容易出现过拟合的情况[2].在实际数据中，除了变量个数远远大于样本个数导致部分传统的变量选择方法不能继续使用，自变量之间存在的多重共线性也会导致模型的稳定性和可预测性降低甚至模型无解，于是统计学者开始了变量系数压缩的研究.Heer[3]在1970年提出了岭回归方法，其思想为在XTX的基础上加了一个较小的扰动约束变量系数，解决了线性回归模型系数无解的问题，使得模型更加稳定，但由于L2范数的限制，岭回归并不具有特征选择的功能；到1996年Tibshirani[4]提出了lasso方法，此方法堪称高维数据统计学领域变量选择的开山之作，其原理与岭回归非常类似，将惩罚项替换成了L1范数，使某些参数变成0，达到了变量稀疏的效果. 1996年至2008年间，统计学者主要针对带有惩罚函数的参数模型和非参数模型进行深入的研究[5，6，7]，如Fan和Li在2001年提出SCAD，Zou和Hastie于2005年提出弹性网络以及Zou在2006年提出Adaptive Lasso等等，但是这些算法都是在变量维数小于样本维数的低维情况下才能够得到较好的结果,并且往往模型形式相对复杂，算法运算速率不高，稳定性欠佳.

为克服基于惩罚项变量选择方法的弊端，相关性类型的变量选择方法应运而生.Fan和Lv[8]通过研究每个自变量与因变量的边际相关性，提出了Sure Independent Screening(SIS)，该方法根据相关系数的大小排序进而筛选出重要变量，充分降低了模型的维度，使得模型简洁高效，开辟出一条基于相关性进行特征筛选的新道路，受到统计学者的广泛关注.近年来，相关性类型的变量选择研究主要集中于边际筛选和联合其他变量选择上.边际筛选方法研究包括继续对边际相关性的研究、对分位数回归和边际误差的研究等[9，10,12，19]，主要有：Szekely，Rizzo等人用距离相关度量(Distance Correlation，DC)取代皮尔逊相关，Li等人提出了在异常值情况下适用的Kendall秩相关方法，Mai和Zou提出了在广义线性模型中能够筛选出不重要信息变量的Kolmogorov-Smirnov统计量，Shao和Zhang提出了衡量预测变量与响应变量间条件平均独立性的鞅差相关系数,Guo等人提出了没有矩条件的稳定相关性筛选法，还有He等人提出了分位数自适应确保独立筛选法，Li等人提出了分位数偏相关系数筛选法等基于分位数或分位数回归的筛选方法，Fan，Feng，Song提出了在非参数可加模型中根据边际残差平方和大小来选择变量的方法，以及Zhu等人在无模型假定下提出了Sure Independent Ranking Screening(SIRS)方法等等.这些方法在实现了快速筛选的同时可能会忽略变量之间的复杂相关性，导致无法准确识别重要信息变量或选入虚假信息变量，因此统计学者又提出了联合变量选择方法，如：Li， Zhong， Zhu提出了基于距离相关性的确保独立筛选变量法(Sure Independent Screening based on Distance Correlation，DC-SIS)和许多文献提出了迭代的变量选择方法，如ISIS，DC-ISIS等等.

尽管基于相关性分析的变量选择方法层出不穷，但研究者依然在探求处理变量间复杂相关关系时能够高效正确地选择重要变量的方法，此外目前该类型的方法在PLS基准模型下的适用性研究还较少，因此，本文提出一种基于马氏距离相关的PLS变量选择思路，建立了基于马氏距离相关t检验的PLS模型(Mahalanobis Distance Correlationt-Teston PLS，MDT-PLS)和基于马氏距离相关性的确保独立筛选变量法PLS模型(Sure Independent Screening based on Mahalanobis Distance Correlation on PLS，MDC-SIS-PLS)，结合PLS模型将其与近年来使用广泛的三种相关性类型的变量选择方法进行对比分析，这三种方法分别为在高维数据独立性下欧氏距离相关t检验[11]的PLS算法(Euclidean Distance Correlationt-Teston PLS，EDT-PLS)、基于确保独立性筛选的PLS算法(SIS-PLS)和基于距离相关性的SIS-PLS方法(DC-SIS-PLS).首先测试了MDT-PLS算法的性能，发现：相比于选用全部解释变量的PLS模型，该算法能够提取出更少的潜变量(latent variables)；相比于在PLS模型中使用基于距离相关系数的向前变量选择算法[22]，MDT-PLS算法的运算效率得到了显著提升；相比于EDT-PLS算法，在保持R2和Q2与其相近的前提下，MDT-PLS能够筛选出更少的信息变量. 接着，又测试了MDC-SIS-PLS算法的性能，发现该算法能够筛选出和SIS-PLS，DC-SIS-PLS相同的变量数目，但是在PLS模型上的R2和Q2明显优于这两种方法，并且具有更小的均方误差(Mean Square Error，MSE).而对于本文的两种方法，MDC-SIS-PLS算法或其迭代算法相比于MDT-PLS总是能够筛选出数目更少的变量与潜变量，缺点为前者牺牲了少许的模型精度.总之，马氏距离相关分析有效解决了变量之间由量纲或相关性带来的干扰问题.

文章结构如下：第2节主要介绍了近年来基于相关性进行变量选择的三种主流方法及本研究所提出的模型与性能评估方式；第3节概述了实验所用的数据集内容；第4节讨论了五种方法在数据集上的结果并给出了合理的解释；第5节对所提出的方法进行了总结.

2 理论与算法

考虑多元线性回归模型

y=Xβ+ε，

(1)

整个PLS算法的优化过程基于文[20]，具体步骤如下.

(1)E0，F0为对设计矩阵和响应矩阵进行标准化处理所得，将其定义为初始残差矩阵；

(2) 提取主成分tk.ωk表示投影方向，满足‖ωk‖=1，k=1,2,3,….tk.ωk满足

tk=Ek-1ωk，

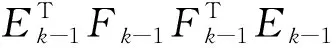
(3) 计算X的载荷pk和y的载荷rk：

(4) 计算残差矩阵Ek,Fk：

循环执行步骤(2)到(4)，直至残差矩阵的精度达到要求.此时若X的秩为A,则可得

(2)

由于t1,…,tA可以表示成标准化自变量矩阵E0的线性组合，因此式(2)可以还原成标准化的因变量关于标准化的自变量的回归方程的形式，即

其中FAk是残差矩阵FA的第k列.

可以看出PLS算法结合了主成分分析、典型相关分析算法，在变量之间存在多重共线性时，算法将变量转化成主成分后再对其进行最小二乘估计，克服了普通最小二乘方法的缺点.

2.1 确保独立筛选法

SIS由Fan和Lv在2008年提出，利用变量之间的皮尔逊相关性对超高维数据筛选变量至相对“温和”的维数，然后再利用比较成熟的变量选择方法对变量进行第二轮筛选.算法思想如下：

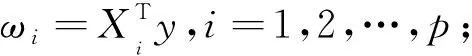
(ii) 将|ωi|进行降序排列，对任意的γ∈(0,1)，取排序后|ωi|的一个子空间

Mγ={1≤i≤p:|ωi|是前[γn]个最大的}，

其中n为样本维数，[γn]表示对γn向下取整；

(iii) 将前[γn]个自变量选入PLS模型.注意，为防止选取变量个数过于保守，本文选取前n/logn个|ωi|对应的变量作为模型的初选变量.

显然该方法能够快速降维，不足之处为当预测变量与因变量之间存在复杂相关性时，就会出现如下两种情况：一是某些本身不重要的自变量由于与重要预测变量之间高度相关而被选入模型；二是某些预测变量与响应变量之间边际相关性不强而联合相关性较高但未被选入模型.为解决此类问题，Fan和Lv提出了SIS的迭代版本(Iterative Sure Independent Screening，ISIS)，以第一轮筛选出的变量建立模型，其残差作为新的响应变量，再与剩下的前n/logn个预测变量进行新一轮的建模，依此下去，得到l个互不相交的变量集合，其并集元素为最终筛选出的变量.可以看出ISIS有效解决了如上所述的第一种不足，但是与响应变量复杂相关的预测变量依旧不能被很好地检测出且计算成本偏高.

2.2 距离相关t检验

2007年Szekely，Rizzo和Bakirow用欧式距离(Euclidean Distance)相关来判断随机变量X和Y是否独立，说明了距离协方差独立性检验对任意维的X，Y均是有效的，但对高维随机变量来讲，仅靠原始相应统计量的值即样本的距离相关系数难以解释X，Y之间的关系. 对此，Szekely，Rizzo于2013年构造了新的检验统计量

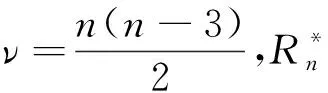
2.3 基于距离相关性的确保独立筛选法

2012年钟威等人提出了DC-SIS，思想与SIS类似，都是用预测变量与响应变量的相关性来衡量预测变量的重要性.不同的是，DC-SIS将皮尔逊相关系数换成了距离相关系数.算法步骤如下.

(i) 首先计算随机变量X和Y的距离协方差：

其中

(ii) 计算样本的距离相关性：

其中c和κ为预先设定的阈值.

(iv) 选取前n/logn个相关系数作为实验指定的阈值.这些相关系数对应的变量为所要筛选的变量.将提取出的变量代入到PLS模型中进行运算.

值得注意的是，当预测变量与响应变量服从正态分布时，基于距离相关的SIS等价于基于皮尔逊相关系数的SIS；当预测变量间存在非线性关系时，筛选性能要优于SIS.

2.4 基于马氏距离的PLS变量选择算法

本文提出了关于马氏距离的PLS变量选择法.如上所述，该方法可分为基于马氏距离相关t检验的PLS算法(MDT-PLS)和基于马氏距离相关确保独立筛选的PLS算法(MDC-SIS-PLS).MDT-PLS算法从高维随机变量独立性假设检验的角度对相关性进行了描述，节省了筛选变量的时间成本；MDC-SIS-PLS算法在保证与SIS和DC-SIS筛选变量个数相同的前提下，有效提高了模型的预测性能.

MDT-PLS算法步骤如下：

(1) 确立原假设H0——高维随机变量X与Y相互独立,备择假设H1——高维随机变量X与Y之间存在相关关系；

(2) 显著性水平设定为0.05；

(4) 根据显著性水平求出检验统计量的拒绝域；

(5) 带入样本计算检验统计量的值并进行判断，若显著性水平小于0.05，则拒绝原假设，说明变量X与Y有相关关系，反之则接受原假设，说明X与Y相互独立.

(6) 将步骤(5)中筛选出的显著性水平小于设定值的变量代入到PLS模型中.

MDC-SIS-PLS算法如下：

(1) 计算成对变量间的马氏距离，得出马氏距离矩阵DM(Xk,Xl)和DM(Yk,Yl). 首先，对于随机变量(X)T=(X1,X2,…,Xp)，用μi表示第i个元素的期望，即μi=E(Xi),i=1,2,…,p,于是变量成对元素间的马氏距离可表示为

其中

同理定义在Rq中的随机变量Y成对元素之间的马氏距离.

(2) 同2.3节所述，计算出马氏距离相关性后替代DC-SIS中的欧氏距离相关性，并按相同的方法筛选出前n/logn个相关系数所对应的变量，代入到PLS模型中.

2.5 模型评估

“没有一种方法可以支配所有的数据集”，所以对于某一特定数据集选择合适的模型显得尤为重要. 预测性能是评价一个模型的好坏的重要指标之一，其表现形式为误差的大小、对数据的解释能力等等. 为不失一般性，本文将所选数据集划分为训练集(Xtrain,ytrain)与测试集(Xtest,ytest),采用预测均方误差根(Mean Square Error)作为第一个评估指标，表达式为

其中N为测试集容量.

另一种选用的模型评估策略使用平方相关系数R2和预测平方相关系数Q2，R2和Q2定义如下：

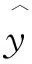
3 数据介绍及软件实现

3.1 蛋黄酱数据集(mayonnaise dataset)

这一数据集包含54种不同植物油类型的蛋黄酱样本(详细介绍见R包“pls”里的开源数据集mayonnaise)，以4 nm为采样间隔，对1 100～2 500 nm波长范围内的样本进行原始的NIR测量，得到351个解释变量，再将54个样本重复测量三次得到的162个光谱数据作为响应变量y. 其中，建立有效的模型以判别蛋黄酱样本中植物油的种类是我们感兴趣的. 另外，实验采用CV方法将数据划分成训练集(70%的样本，113个样本)和测试集(30%的样本，49个样本).

3.2 啤酒数据集(beer dataset)

整个数据集包含60个未稀释的脱气啤酒样本，于30 mm的石英池中被记录，测量的光谱波长范围为1 100 nm～2 250 nm，采样间隔为2 nm，共获取576个波长点作为预测变量X.其中，啤酒原始提取物的浓度是本研究感兴趣的.此外，我们将该数据集随机分割成一个包含70%数据的训练集和一个包含30%数据的测试集，两数据集不相交.

3.3 汽油数据集(gasoline dataset)

该数据集来源于R包“pls”，包含60个具有特定辛烷值的汽油样品，以2 nm为间隔在900～1 700 nm的波长范围内得到401个近红外光谱数据.我们以60个汽油样品为因变量，401个数据点为自变量建立模型，致力于利用近红外光谱技术提升测定辛烷值的效率、节省成本. 此外，利用LOO法将数据随机分割成包含70%样本的训练集和包含剩余样本的测试集.

3.4 软件实现

本文所有的代码和实验都是在R软件4.0.3版本(https://www.r-project.org/)下实现的.在建模过程中pls包用于构建pls模型，dcov包用于快速提取距离相关系数，energy包用于实施高维多元独立性的非参数t检验，OHPL包用于提供数据.

4 结果与讨论

为更好地评估马氏距离相关在PLS模型上的预测性能，我们在上述四个数据集上应用PLS模型对各种方法进行比较测试，并且考虑到所选基础模型的适用性问题，PLS模型也纳入比较范围.同时为保证实验结果的可靠性与稳定性，本研究将对每个数据集进行随机分割100次的实验，以100次实验的均值为最终的评估结果.

4.1 蛋黄酱数据集(mayonnaise dataset)

表1给出了不同方法在蛋黄酱数据集上的结果.从表1我们发现相较于使用全部变量的PLS模型，MDT-PLS算法的nLV值减少了10个，R2和Q2依然保持在98%和85%以上，而且从nVAR值和nLV值看，MDT-PLS算法的变量选择能力要高于EDT-PLS算法.此外，就三种关于确保独立筛选方法的模型而言，表1只给出了两次的迭代结果，在迭代过程中，MDC-ISIS-PLS算法对模型的解释能力和稳定性都显著高于另外两种算法. 如此继续迭代下去，MDC-ISIS-PLS在同类型的算法中继续保持优势，当第五次迭代结束即MDC-ISIS-PLS算法获取的nVAR，nLV值分别为160和24时，该算法与MDT-PLS算法的预测性能能够达到十分接近的程度.

表1 蛋黄酱数据集上不同方法的评估结果

图1展示了蛋黄酱数据集的光谱图及不同方法筛选变量的波长分布. 从图中我们可以看到MDT-PLS算法识别的四个波长间隔大部分包含在EDT-PLS算法识别的波长区域里，并且被MDT-PLS算法选择而未被EDT-PLS算法选择的1 676～1 716 nm、2 132～2 152 nm、2 164～2 244 nm等五个波长区域也都不同程度被其他几种算法所识别，说明MDT-PLS算法相比于EDT-PLS算法具有更好的发现重要变量的能力. 另外，MDC-ISIS-PLS算法识别的六个波长区域分别位于1 212～1 220 nm，1 448～1 504 nm，1 696～1 768 nm，1 820 nm，1 912～1 976 nm，2 252～2 284 nm中，与ISIS-PLS算法选择的波长十分相似.根据对RMSEP值和R2、Q2的分析，MDC-ISIS-PLS算法相较于其同类型算法所筛选的变量更具代表性，并且能够有效提升模型的预测性能.

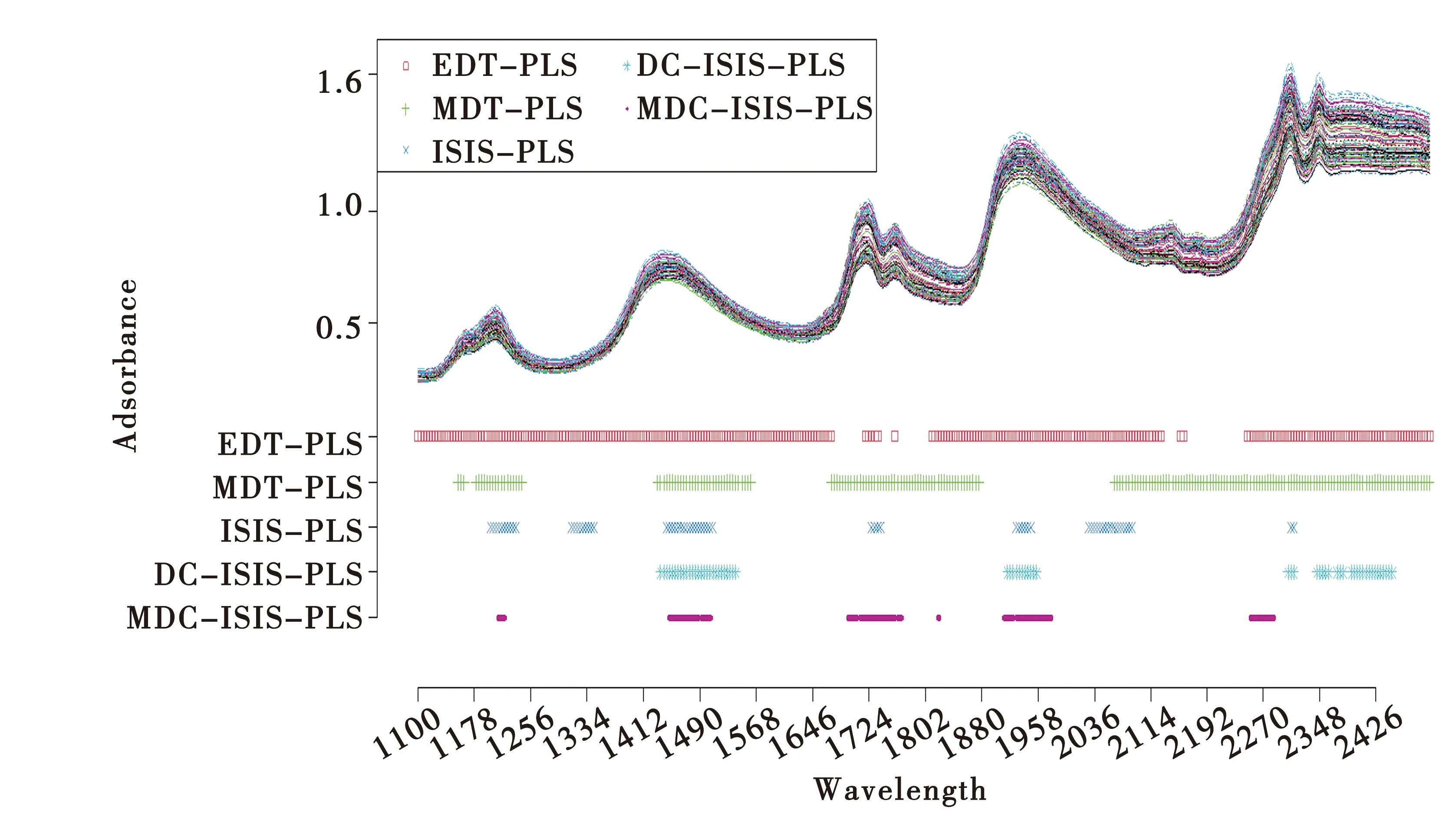
图1 蛋黄酱数据集上不同方法变量选择的结果

4.2 啤酒数据集(beer dataset)

对于啤酒数据集，表2列出了不同方法的全部结果.根据表2我们可以看到相比于使用了全部信息变量的PLS算法，本研究所用的5种方法具有更高的预测性能.其中，MDT-PLS算法的nVAR和nLV值都远小于EDT-PLS，对模型的解释能力也超过了98%.出于变量选择的角度，MDT会成为距离相关t检验在PLS模型上的首选. 另外，SIS-PLS和DC-SIS-PLS算法的预测性能表现一致，相较于这两种算法，MDC-SIS-PLS算法在100次实验中的RMSEP均值及标准差都有显著降低，说明该算法得到的模型更加精确和稳健.

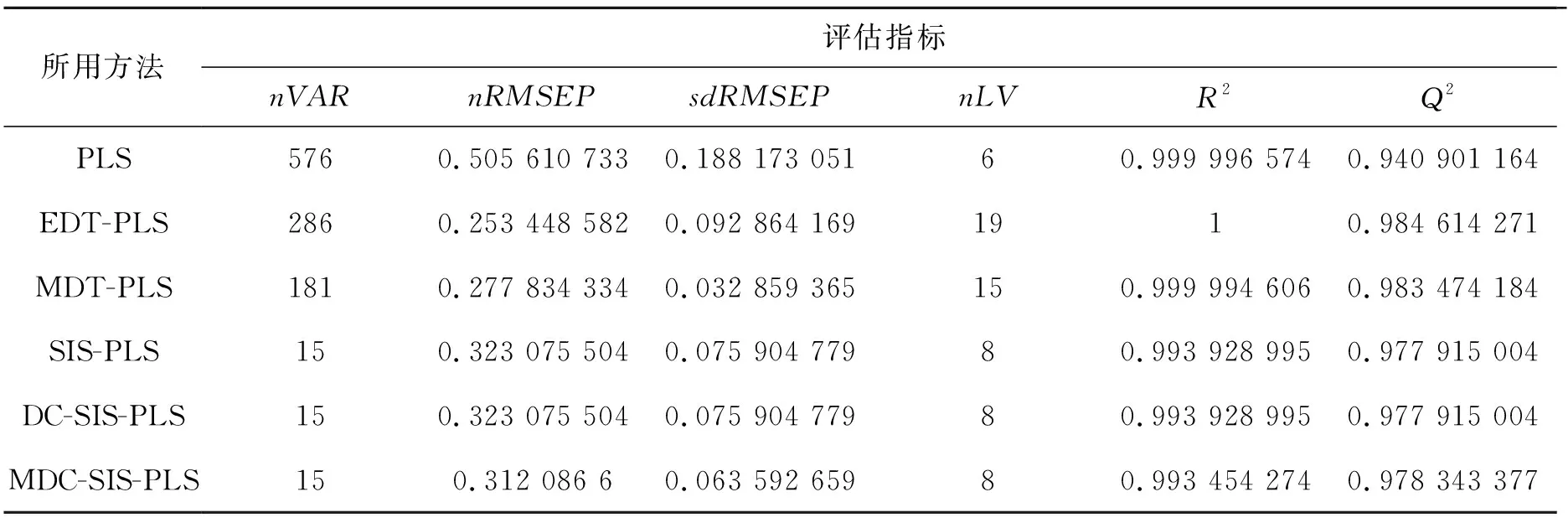
表2 啤酒数据集上不同方法的评估结果

图2展示了该数据集上的光谱图和五种方法所选择的变量. 可以看出EDT-PLS算法选择了最大数量的变量，MDT-PLS次之，三种基于SIS变量选择方法筛选的变量个数相等，并且远远小于基于距离相关t检验的这两种方法.如前所述，SIS-PLS和DC-SIS-PLS算法所选择的波长相同，主要集中于1 304～1 332 nm中，而MDC-SIS-PLS算法识别出的波长位于1 296～1 326 nm中，根据对上述评估结果的分析知MDC-SIS-PLS算法所筛选的变量更加准确.

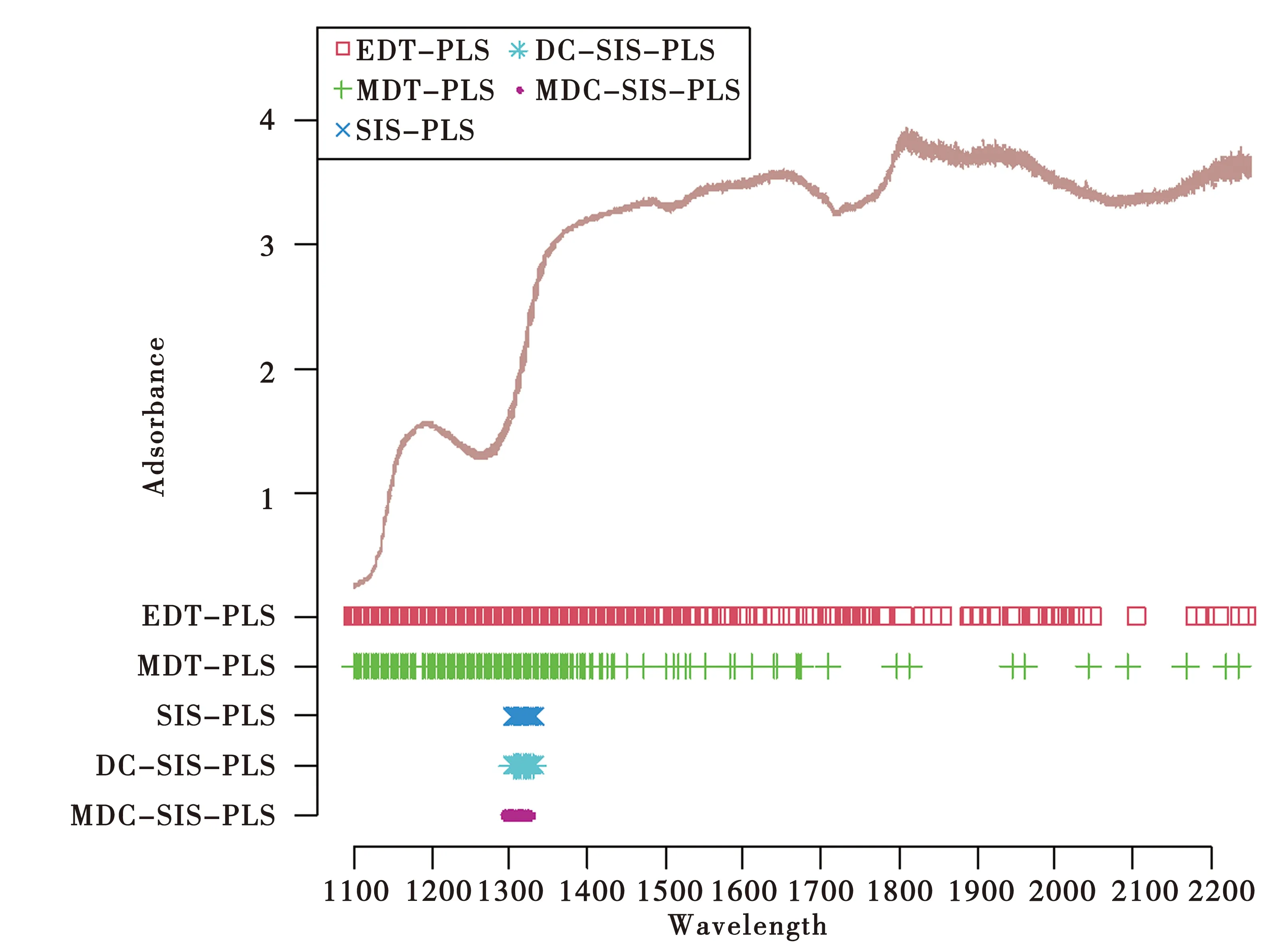
图2 啤酒数据集上不同方法变量选择的结果

4.3 汽油数据集(gasoline dataset)

汽油数据集上不同方法的评估结果见表3.我们观察到在几乎同等模型解释能力的情况下，EDT-PLS算法使用的nVAR相对于PLS模型减少了185个，并且提取出了与PLS模型相近个数的主成分；MDT-PLS算法获取的nVAR相对于PLS模型降低了350个，对模型的解释能力依然保持在较高水平，但提取的主成分个数增加了5个，RMSEP值及其标准差增加了0.04左右，说明MDT-PLS模型在保证模型精度不受过多影响的前提下提升了变量选择的能力；另外，采用SIS算法的这几种方法的评估指标完全吻合，说明在所给数据集预测变量间没有量纲变化或相关性影响的条件下，MDC-SIS-PLS算法与SIS-PLS,DC-SIS-PLS算法能够达到一致的预测性能.

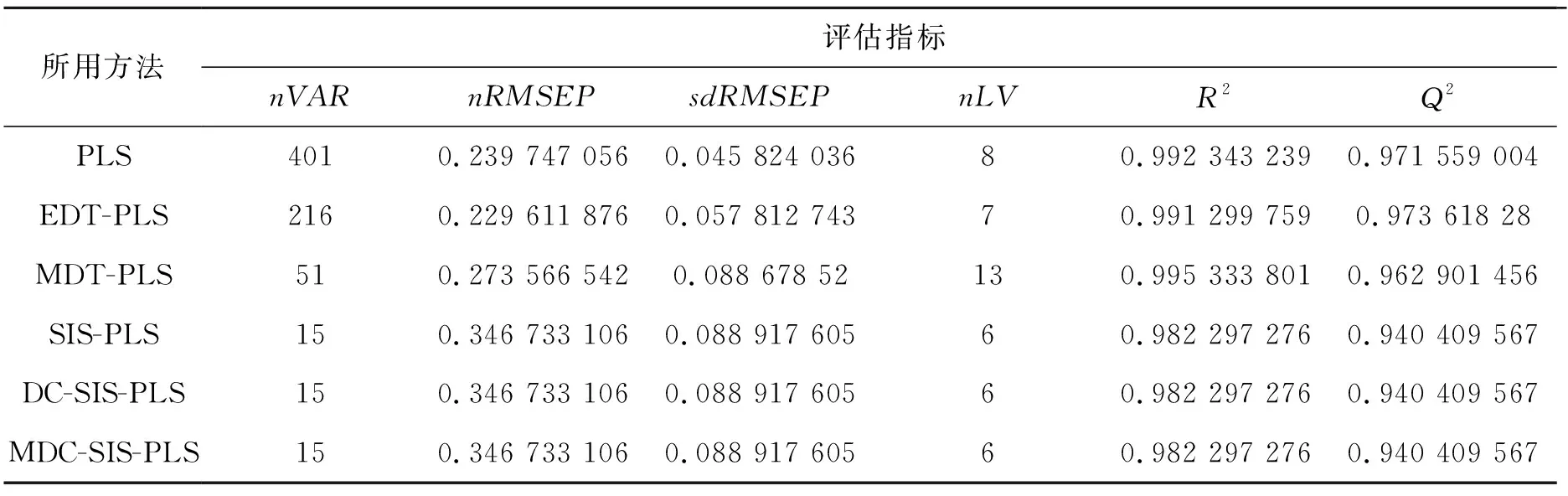
表3 汽油数据集上不同方法的评估结果

图3展示了汽油数据集上的光谱图和五种方法所选择的变量分布. 直观来看，SIS-PLS、DC-SIS-PLS、MDC-SIS-PLS这三种算法筛选的波长区域都为1 200～1 228 nm，进一步说明了MDC-SIS-PLS算法的表现性能在没有其他因素影响的条件下可以与经典的SIS-PLS、DC-SIS-PLS算法一致；而MDT-PLS算法识别的5个波长间隔基本都包含在EDT-PLS算法识别的波长区域内，1 692 nm是唯一一个EDT-PLS算法没有识别出的波长点，并且其他四个波长间隔也较为分散，由此可以推知该算法提取主成分个数偏多的原因.

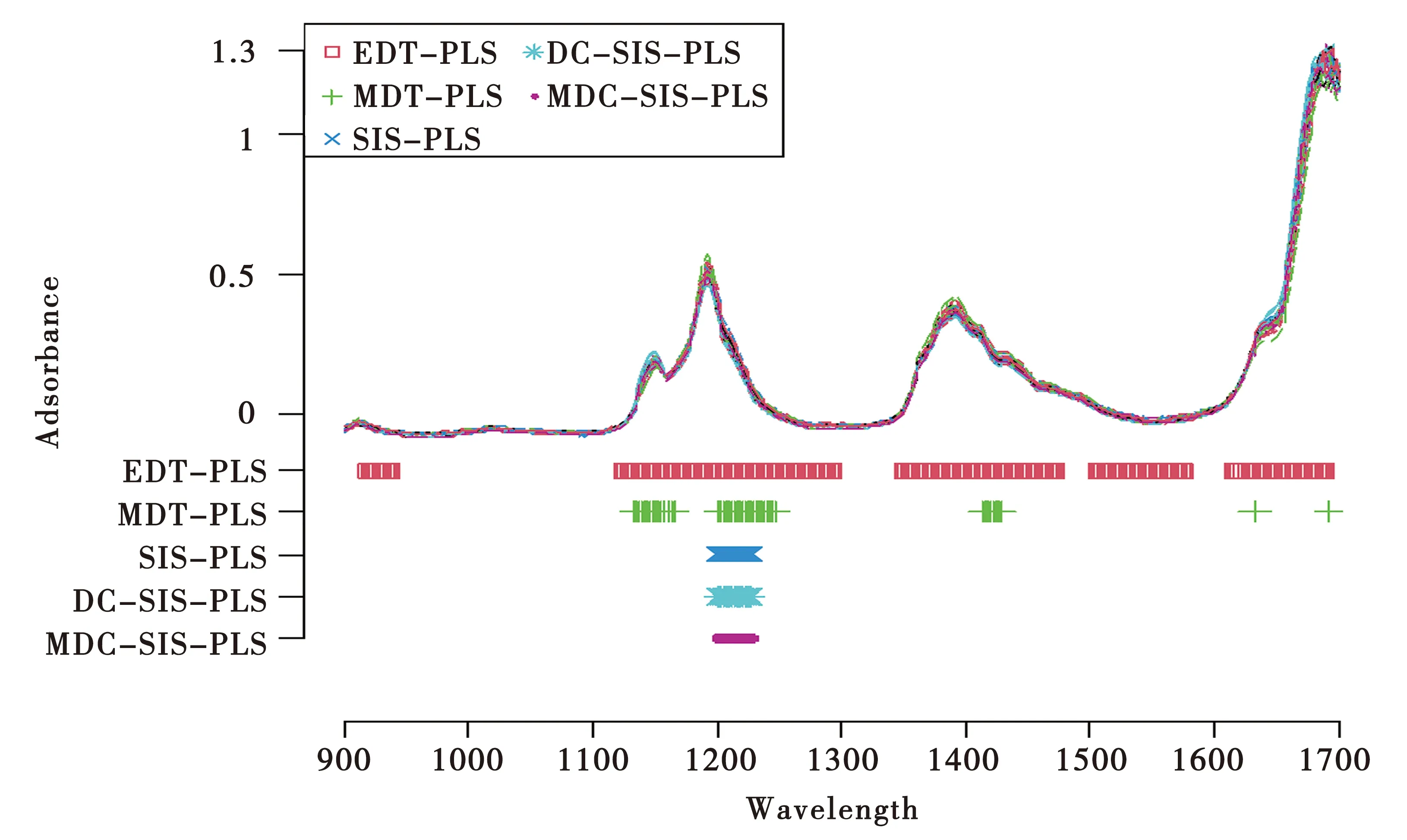
图3 汽油数据集上不同方法变量选择的结果

5 结论

在本文中，我们将基于欧氏距离相关性的研究成果拓展到马氏距离理论上来，在PLS模型上应用马氏距离相关t检验算法(MDT)、基于确保独立筛选的马氏距离相关系数算法(MDC-SIS)，并且在真实的光谱数据上进行了实验. 结果表明，在马氏距离不受协方差矩阵等不稳定因素影响即计算顺利的情况下，MDT-PLS、MDC-SIS-PLS这两种算法能够在与同类型算法比较中表现出其优良的变量选择能力和预测性能，并且模型的稳健性也较高，极大程度上消除了基于距离相关系数筛选变量速率慢和确保独立性筛选方法由于自变量间高度相关却与因变量无关而被选入特征模型的弊端.

对比本文提出的两种算法，MDT-PLS算法和MDC-SIS-PLS算法，即使MDC-SIS-PLS算法已经采用了迭代算法，前者也倾向于选择更多的变量，提取更多的主成分个数，对模型的解释能力自然也高于后者.但更多情况下，MDC-SIS-PLS算法或进行迭代后的算法的预测性能可以达到较高水平或与MDT-PLS算法相差无几，与此同时，对重要变量的提取能力也优于MDT-PLS算法，因此，MDC-SIS-PLS算法仍然是一个较好的选择.